修正空时自适应处理在水下自导系统中的应用
2012-02-23吕维王志杰李建辰王明洲胡桥杨宝民
吕维,王志杰,李建辰,王明洲,胡桥,杨宝民
(1.中国船舶重工集团公司 第705 研究所,陕西 西安710075;2.中国船舶重工集团公司 第705 研究所 水下信息与控制重点实验室,陕西 西安710075)
0 引言
混响是水下自导系统主动工作方式特有的干扰,在浅海环境下界面混响影响尤为严重,直接影响自导系统主动回波的信号检测能力。不同于海洋噪声,混响是由发射信号引起的,其谱结构与发射信号具有一定的相似性,当水下自导发射波束触及界面时,混响将从不同的锥角入射,造成多普勒扩展。混响谱的扩展证明混响也具有空时耦合的特性,这与机载PD 雷达杂波谱扩展特性相近。自1973年Brennan 等首次提出了空时二维自适应处理(STAP)的概念[1],而后一些学者将空时自适应处理应用到了雷达信号处理[2-5]。他们的研究表明:STAP 技术能够从空间和时间二维同时区分目标和杂波,因而在雷达杂波抑制上具有明显的性能优势[6-10]。同样,STAP 的方法也适合于抗混响处理[11-14]。
从目前国内外公开报道的文献来看,STAP 用于混响的抑制仅仅处于起步阶段。文献[11 -14]虽然研究了STAP 方法在水下环境中的应用,指出对于提高主动声纳混响抑制有一定的能力,但并没有考虑到与雷达杂波环境不同:水下环境的声速远比电磁波低,散射点的运动对混响回波波形的影响往往不能忽略,即回波信号不仅在时宽和幅度受到压缩和扩展,还产生了频率的调制和扩展,所以雷达空时自适应处理方法应用在水下自导系统时必须进行修正和改进。本文结合空时自适应原理和水下自导系统目标回波模型,对应用于水下环境的空时自适应方法进行改进,并针对回波的空-时耦合项,分析了应用空-时耦合导向矢量对混响抑制以及目标检测能力的影响。
1 STAP 原理
1.1 雷达目标回波
为了分析STAP,首先讨论雷达目标回波模型。采用N 元均匀水平前视线阵,阵元间隔d =λ/2,以速度vp匀速运动,且时域采样点数为M,发射信号中心频率为f0,时间采样频率为fs.考虑雷达电磁环境满足c=3 ×108m/s≫vp,因此可以得到第n 个阵元(距离阵中心的第n 个阵元)接收到目标回波信号的第m 个采样点的信号形式如(1)式所示[17]。

式中:u(t)表示发射信号包络;α、θ 分别表示雷达目标的空间方位角和俯仰角;r0表示雷达目标的到阵元中心的径向距离;v0表示目标与雷达运动基阵的相对径向运动速度;xn为目标与阵元n 的距离相对于阵元中心径向距离的路程差,xn=ndsin αcos θ/c.
1.2 STAP 原理
STAP 的实质是空时二维最优处理,利用STAP抑制杂波,即先求解杂波加噪声的协方差矩阵Q,再求解每一个空时采样点xnm(为实际数据矢量,可能为噪声或噪声加信号)的加权系数wnm(可表示为矢量形式,即W =[w11,w21,…,wnm]T),最后将所有的空时采样进行复加权并求和输出[1-3],如(2)式所示

式中:X 为X=[x11,x21,…,xnm]T;H 表示矢量或矩阵的共轭转置。自适应权矢量W 是通过线性约束使得杂波输出功率最小,而在感兴趣的方向达到最大准则确定,即自适应权值满足(3)式的约束条件。

求解上式可以得到最优权值为Wopt=μQ-1S.S=St(ωt)⊗Ss(ωs)表示NM×1 维空时二维导向矢量,St(ωt)和Ss(ωs)分别表示时域(多普勒域)和空域导向矢量,如(4)式、(5)式所示。ωt和ωs分别为时域(多普勒域)和空域角频率(如(6)式、(7)式所示);fD为多普勒频率,fD=2v0/λ.
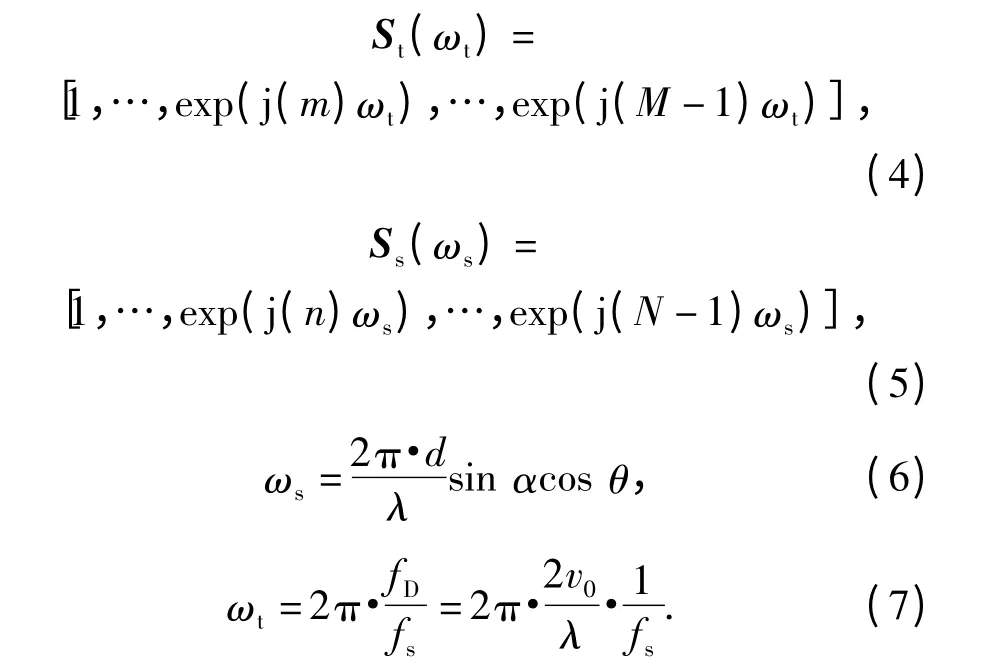
将(4)式~(7)式与(1)式中的exp{j2π((mfD/fs/1)+(ndsinαcosθ/λ/2))}进行比较可以看出:空时导向矢量Ss(ωs)和St(ωt)正好分别与(1)式雷达目标回波模型中 exp {j2π ((mfD/fs/1)+(ndsinαcosθ/λ/2))}的第2 项和第1 项相匹配。因此利用空时导向矢量的物理含义可理解为:空域和时域(多普勒域)导向矢量实质是在空间、时间进行搜索匹配的过程。雷达STAP 就是在满足最优处理的条件下,通过空时导向矢量搜索进行杂波抑制和目标检测的。
2 水下自导系统目标回波
为了研究空时自适应原理在水下自导系统中的应用,首先分析水下自导系统目标回波模型,假设自导平台基阵为N 元均匀水平前视线阵,阵元间隔d'=λ'/2,自导平台以速度v'p匀速运动,且时域采样点数为M,发射信号中心频率为f'0,时间采样频率为f's.考虑到鱼雷水下环境的声速远比电磁波低,且不满足c'≈1 500 m/s≫v'p条件,因此目标运动对回波波形的影响往往不能忽略,即回波信号不仅在时宽和幅度受到压缩和扩展,还产生了频率的调制和扩展[15],所以雷达目标回波的窄带模型在水下混响回波中并不适用。因此自导基阵的第n 个阵元(距离阵中心的第n 个阵元)接收到目标回波的第m 个采样点的信号形式可以写为如(8)式所示:

式中:u(t)表示发射信号形式;时间尺度κ =1 +β =1 +2v'0/(c' -v')(反映了目标与自导平台间相对运动时产生的波形压缩和扩展);α、θ 分别表示目标的空间方位角和俯仰角;r'0表示水下目标的到阵元中心的径向距离;v'0=v'pcosαcosθ 表示目标与运动平台的相对径向运动速度;f'D为多普勒频率(f'D=βf'0);x'n为目标与第n 个阵元的距离相对于阵元中心径向距离的声程差,x'n=(nd'sin αcos θ)/c',n=1,2,…,N.
3 水下自导系统目标回波空时耦合及修正空时自适应处理
3.1 回波空时耦合项的产生
根据雷达空时自适应理论,可知应用空时自适应理论首先需要求出混响加噪声的协方差矩阵R,然后结合水下目标的空时导向矢量S'求出最优权值

根据第2 节中分析的空时导向矢量的物理含义,结合(8)式声纳目标回波模型中exp{j2π[(mf'D/f's/1)+(nd'sin αcos θ/λ'/2)+(f'Dx'n/3)]}的第1项和第2 项,分别对混响空时自适应的时空导向矢量做以下修正:这里S' =S't(ω't)⊗S's(ω's)表示NM×1 维空时(多普勒)二维导向矢量。S't(ω't)和S's(ω's)分别表示时域(多普勒域)和空域导向矢量(如(10)式~(11)式所示)。ω't和ω's分别为时域(多普勒域)和空域角频率,如(12)式~(13)式所示;⊗为kronecker 乘积符号。

比较(1)式雷达目标回波和(8)式水下声纳目标回波模型,可以看出(8)式exp{j2π[(mf'D/f's/1)+(nd'sin αcos θ/λ'/2)+ (f'Dx'n/3)]}中多出了第3项,即空时耦合项f'Dx'n.由于水下环境不满足:c'≫v'0,因此,此项不能省略,所以需要据此空时耦合项对导向矢量进行修正,即增加空时耦合导向矢量S'st(ω'st),如(14)式所示。ω'st为空时耦合角频率,如(15)式其中。[f'D][M,1]表示将f'D扩展为M×1 维矢量。

因此混响空时导向矢量应最终修正为(16)式,

3.2 空时耦合导向矢量的物理意义
在第2 节中,通过分析得出:使用空时导向矢量的实质是.在空时(多普勒)二维空间上进行搜索匹配以实现噪声抑制和目标检测。从(10)式~(13)式可知:时域(多普勒域)导向矢量S't(ωt)∈CM和空域导向矢量S's(ωs)∈CN分别利用时域角频率(多普勒域)ω't和空域角频率ω's实现搜索匹配。分析空时耦合导向矢量S'st(ω't,ω's)∈CN的表达式可知,其空时耦合角频率ω'st既含有空域搜索信息x'n、又含有时域(多普勒域)搜索信息f'D,是一个满足空间、时间(多普勒)耦合的搜索信息量,它从本质上修正了空时导向矢量;但是由于其矢量n 维信息是从空间角度(exp(j(n)ω'st))考虑的,因此也可以作为空域修正矢量,这对于匹配检测的精确角度估计具有重要意义,下面将通过仿真实验进一步验证空时耦合项的物理意义。
4 仿真结果
仿真实验中相关参数:由于目前水下自导系统采用的基阵大多为平面阵,一般可等效为一线阵,因此本文采用以8 个基元按半波长排列的均匀线阵(前视阵),且都为理想基元,即不考虑幅度和相位误差,基阵距海平面40 m.发射CW 脉冲载波频率f'0=15 kHz,脉宽为T' =30 ms,时域采样频率f's=2 kHz(采用基频采样),平台运动速度为v'p=25 m/s.仿真信号的混响噪声比为RNR =26 dB,信号噪声比为SNR= -18 dB.仿真目标出现在α =10°(正前方为0°)方向上,目标运动速度v =3 m/s(v =0.5 m/s),目标运动方向与目标、基阵主轴连线夹角为γt=10°,因此目标的多普勒频率为fDt1=439.7 Hz(fDt2=490.3 Hz).
4.1 混响多普勒谱f'r-α 轨迹
首先分析单一距离环(即θ 恒定)上(只考虑界面混响),混响多普勒谱f'r-α 轨迹。f'r表示归一化多普勒,α 表示空间方位角。由第3 节可知,混响的多普勒频率为f'd= βf'0,所以归一化多普勒频率为可见f'r-α 轨迹与θ(即r/H)和v'p有关。当固定v'p=25 m/s 时,其混响轨迹随r/H 变化曲线如图1所示;当固定r/H,其混响轨迹随v'p的变化曲线如图2所示。
下面利用高分辨力功率谱估计器对混响进行空时谱估计。利用(17)式所示的最小方差估计器进行估计,得到的单一距离上的混响空时谱,如图3所示。从图中可以看出:混响功率谱的覆盖区域是在归一化多普勒频率方位角平面上以α=0°为轴的曲线,与上述理论分析结果相符。
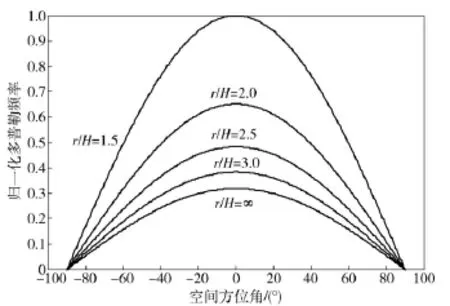
图1 混响的f'r-α 轨迹1Fig.1 f'r-α curves of reverberation based on r/H

图2 混响的f'r -α 轨迹2Fig.2 f'r -α curves of reverberation based on vp
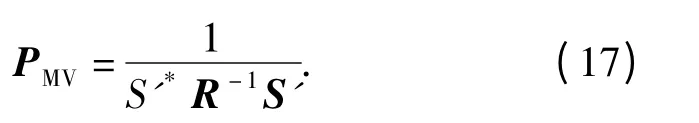
4.2 改善因子

图3 混响的空时二维功率谱Fig.3 The power spectrum of reverberation
改善因子(IF)在一定程度上反映了空时自适应的混响抑制和低速目标检测能力。图4给出了空时处理方法在导向矢量修正前、后的各自改善因子,从图中可以看出:修正导向矢量后改善因子抑制噪声的能力有所提高(有较高的分贝数),而且对于低速目标的能力也进一步改善(-3 dB 多普勒频率更接近1).

图4 改善因子Fig.4 Improvement factor
4.3 目标检测与估计
采用空时处理器的最大输出幅度作为目标检测的标准,图5、图6分别给出了修正导向矢量前、后的最优处理结果(目标速度为vt1=3 m/s).比较图5、图6可以看出:修改导向矢量后的最优处理结果主瓣波束宽度相对较窄,因此修改导向矢量后对目标检测能力有所提高。
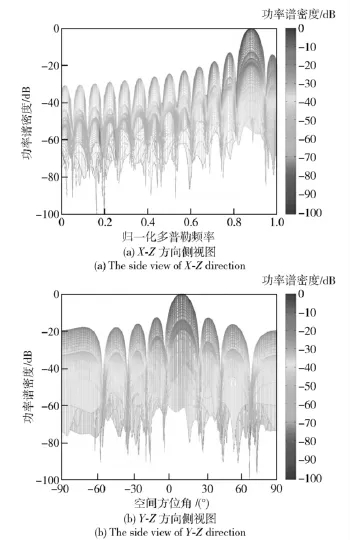
图5 修改导向矢量前的最优处理结果Fig.5 Output of optimal processing before modifying steering vector
第4.2 节中分析了空时耦合导向矢量物理意义,为了验证这一理论,下面从目标检测角度分析空时耦合导向矢量的意义,假设目标的信息如前文所述(αt=10°、fDt2=490.3 Hz).分别列出目标检测结果在不考虑空时耦合导向矢量时的目标检测结果如图7所示,以及考虑空时耦合导向矢量时的目标检测结果如图8所示。求出两种情况下的目标检测结果得到:第1 种情况下:检测目标方位=10.5°(方位估计误差0.5°)=487.2 Hz 目标多普勒;第2种情况下:目标方位=10°(方位估计误差0°)、目标多普勒=487.2 Hz.比较两种情况下的目标检测结果可知,考虑空时导向矢量时目标检测结果的方位估计更逼近真实目标,但对多普勒估计却没有明显改善。因此说明,空时耦合导向矢量虽然同时包含时域、空域导向矢量信息,但实际是对空域的修正矢量,提高了目标方位估计的能力。
5 总结
与雷达杂波相似,混响谱也具有扩展特性。近年来,利用混响谱扩展特性,采用空时自适应方法进行用于水下混响抑制和运动目标检测受到越来越多的关注。为了将STAP 用于水下自导系统,从而解决浅水抗混响问题,针对声纳回波的空时耦合性对空时自适应方法进行修正,并提出了应用空时耦合导向矢量进行空时处理。通过仿真分析,可得到以下结论:
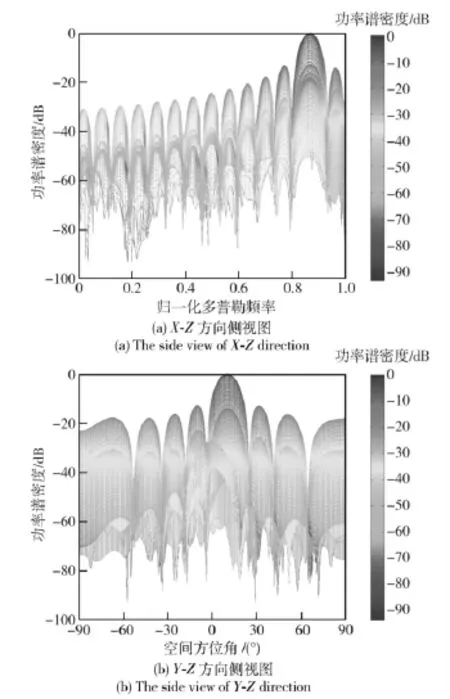
图6 修改导向矢量后的最优处理结果Fig.6 Output of optimal processing after modifying steering vector

图7 不考虑空-时耦合导向矢量时的目标检测结果Fig.7 Results of target detection without considering Space-time coupling steering vector
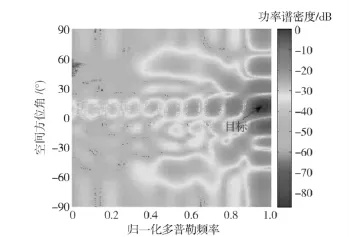
图8 考虑空时耦合导向矢量时的目标检测结果Fig.8 Results of target detection considering Space-time coupling steering vector
1)在应用于水下空时自适应修正理论的基础上,通过仿真验证,证明了混响具有特有空时特性,对工程实际应用空时自适应理论进行混响抑制具有一定的意义。
2)修改后的空时处理方法更适合水下环境,提高了混响抑制和目标检测的能力;
3)空时耦合导向矢量虽然同时包含时域、空域导向矢量信息,但实际是对空域的修正矢量,提高了目标方位估计的能力。
References)
[1] Brennan L E,Reed I S.Theory of adaptive radar[J].IEEE Transactions on Aerospace and Electronic Systems,1973,9(2):237 -252.
[2] Kremm R.Principles of space-time adaptive processing [M].London:The Institution of Electrical Engineers,2002:467 -537.
[3] Guerci J R.Space time adaptive processing for radar[M].Boston:Artech House,2003:1 -72.
[4] Melvin M L.A STAP overview[J].IEEE Aerospace and Electronic System Magazine,2004,19(1):19 -33.
[5] Farina A,Timmoneri L.Adaptive array of antennas and STAP[J].IEEE International Symposium on Phased array Systems and Technology,2003,10(2):14 -17.
[6] 吴仁彪,贾琼琼,李海.机载雷达高速空中微弱动目标检测新方法[J].电子与信息学报,2011,33(6):1460 -1463.WU Ren-biao,JIA Qiong-qiong,LI Hai.Detection of fast moving dim targets on airborne radar via STAP[J].Journal of Electronics& Information Technology,2011,33(6):1460 -1463.(in Chinese)
[7] Yan Zhang,Yunhua Zhang,Xiang Gu.Improved STAP algorithm based on APES[J].Journal of Systems Engineering and Electronics,2011,22(3):387 -392.
[8] 段克清,谢文冲,王永良,等.一种稳健的共形阵机载雷达杂波抑制方法[J].电子学报,2011,39(6):1321 -1326.DUAN Ke-qing,XIE Wen-chong,WANG Yong-liang,et al.A robust clutter suppression method for airborne radar with conformal antenna s array[J].Acta Electronica Sinica,2011,39(6):1321-1326.(in Chinese)
[9] Richardson P G,Hyaward S D.Adaptive space-time processing for forward looking radar[C]∥Proceedings of the IEEE 1996 International Radar Conf.Ano Arbor,MI,USA:IEEE,1996.
[10] Czernik R J.An application of space-time adptive processive processing to airborne and airborne and spaceorne monostatic and bistatic radar systems[D].Hudson Hoboken:The Faculty of the Stevens Instituete of Technology,2010.
[11] Kremm R.Detection of slow targets by a moving active sonar[J].Acoustic Signal Processing for Ocean Exploration,1993,388(5):165 -170.
[12] Mio K,Chocheyras Y,Doisy Y,et al.Space time adaptive processing for low frequency sonar[J].Oceans Conference Record(IEEE),2000,(9):1315 -1319.
[13] 赵申东,唐劲松,蔡志明.梳状谱信号的空时自适应处理[J].武汉理工大学学报:交通科学与工程版,2008,32(5):937 -940.ZHAO Shen-dong,TANG Jin-song,CAI Zhi-ming.Space-time adaptive processing of LFM[J].Journal of Wuhan University of Technology:Transportation Science & Engineering,2008,32(5):937 -940.(in Chinese)
[14] 詹昊可,蔡志明,苑秉成.鱼雷声纳空时自适应混响抑制方法[J].武汉理工大学学报:交通科学与工程版,2007,31(6):1 -3.ZHAN Hao-ke,CAI Zhi-ming,YUAN Bing-cheng.Space-time adaptive processing of LFM[J].Journal of Wuhan University of Technology:Transportation Science & Engineering,2007,31(6):1 -3.(in Chinese)
[15] 朱埜.主动声呐检测信息原理[M].北京:海洋出版社,1990:50 -53.ZHU Ye.Principles of active sonar detection[M].Beijing:Ocean Press,1990:50 -53.(in Chinese)
