不同网格划分方式的圆柱型舵杆绕流数值模拟结果比较
2012-02-21周上然
周上然
(海军上海地区装备修理监修室,上海 200000)
船舶在航行时,流体经过舵杆会产生涡。雷诺数在一定范围时,流体在舵杆表面的后驻点附近脱落,脱落漩涡以周期性的交替方式离开圆柱表面,形成涡泄。涡泄的存在使得舵杆表面周期性变化的升力和阻力增加,从而导致物体的振动,影响了舵杆的稳定性。本文将舵杆简化为二维圆柱模型,运用两种网格划分方式模拟Re=200时二维静止圆柱的绕流情况,对模拟出的升力与阻力系数进行比较与分析。
1 数值建模
1.1 基本方程及边界条件
对不可压缩粘性流体,在直角坐标系下,其运动规律可用N-S方程来描述,连续性方程和动量方程分别为

式中:
ui、uj分别为 x、y 方向的速度;
ρ为空气密度;
p为压力;
ν为流体动力粘度系数。
选取整个流场区域大小为30 D×55 D(D为立管直径,D=0.02 m,ν=0.010 03 m/s),其中,上游为15 D,下游为40 D,立管圆心距上下两侧各15 D,左侧、上侧与下侧设为速度入口,流体自左向右流动,右侧为速度出口,圆柱壁面满足无滑移固壁条件。本算例中雷诺数为200为层流流动,因此,在粘性模型的选取上采用Laminar层流模型。在计算方法上采用SIMPLEC方法,由于流动为非定常流动,为模拟瞬态流动,时间离散方式采用二阶隐式,对压力项离散格式采用二阶精度。
1.2 网格划分
流场计算区域选为55 D×30 D,圆柱距入口边界为15 D,上下边界距圆柱为15 D,D为物体垂直于来流方向平面上的特征尺寸,对圆柱一般取直径,D=0.02 m,ν=0.010 03 m/s。
网格高度对于计算结果是否精确有着决定性的作用,对于层流模型,圆柱近壁处第一层网格高度需要满足y+≈1,根据如下公式估算第一层网格控制点离开壁面距离△y:

第一种方法对计算区域进行了划分,中心圆柱采用O型网格并进行局部加密,右侧采用渐变的结构网格以提高计算效率,如图1所示。第二种方法将全流场分为9个区域,采用四边形结构网格对中间圆柱周围4D区域及尾流区进行局部加密,如图2所示。

图1 网格划分

图2 网格划分
1.3 计算结果及分析
图3、4分别为第一种与第二种网格划分(Re=200)时的涡街脱落图。
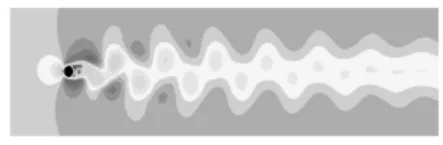
图3 涡街脱落图

图4 涡街脱落图
两种网格模拟的现象清晰,基本相同,可以认定两种方式均可以模拟光滑圆柱舵杆绕流。
2 模拟结果的比较与分析
2.1 升力系数与阻力系数的分析
图3、图4的现象清晰的模拟了光滑立管尾流场,因此,可认为两种划分方式均可行。图5、图6分别给出了两种不同划分格式的圆柱阻力系数与升力系数的时程曲线。从图上可以看出圆柱尾流形成了卡门涡街,流动在150 s后趋于稳定,当位于圆柱上侧的旋涡脱落后,圆柱上方压力增加,此时圆柱下方旋涡还未脱落,压力较小,上下两侧产生负的压力差,反之当位于圆柱下侧的旋涡脱落时,产生正的压力差,因此,升力系数以y=0为平衡位置进行周期性震荡,升力系数的均值为0。升力系数与阻力系数曲线在涡稳定脱落后,均呈现周期性变化[1]。两种划分方式计算出的结果:
(1)升力系数幅值为0.51,阻力系数在涡脱达到稳定后的均值为1.23。
(2)升力系数幅值为0.53,阻力系数在涡脱达到稳定后的均值为1.32。
从升力系数和阻力系数的周期性变化中,可以清楚的反映出圆柱上旋涡脱落的特性。均匀来流经过圆柱表面时,流动发生变化,产生边界层分离后,在逆压梯度的作用下,于圆柱上下两个表面附近产生旋涡,旋涡在来流的作用下随着流体向后运动,然后脱落。由于圆柱上下两侧的旋涡变化对流动方向上的压差影响是一样的,所以来流压力差的变化,较垂直来流方向的压力差变化快,变化速度是它的两倍,这就很好的解释了阻力系数的振荡周期为升力系数振荡周期的二分之一。

图5 第一种划分方式

图6 第二种划分方式
对升力系数时程曲线做傅里叶变换,从时域转换到频域,第一种划分方式计算出的主频率为0.095 Hz,如图7所示,第二种划分方式计算出的主频率为0.102 Hz,如图8所示。

图7 第一种划分方式升力系数时程谱

图8 第二种划分方式升力系数时程谱
2.2 斯特劳哈数(St)
St数是描述圆柱绕流的一个重要参数,其将边界层分离及流动的不稳定性这些微观的随机特性,与表现相对稳定性的涡泄频率联系在一起[2],其定义为
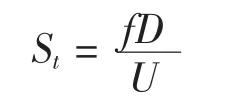
式中:
St为Strouhal数,表示旋涡的脱离情况;
f为圆柱涡泄频率;
U为未受干扰的自由来流速度。
一般而言,在绝大多数的Re数区域内,St数相对稳定,这意味着涡泄有序。第一种划分方式计算出Strouhal数为0.19,第二种划分方式计算出Strouhal数为0.2。
2.3 结果比较
表1中给出了国内外的研究学者对雷诺数为200时的圆柱绕流数值计算[3]与实验结果,通过比较,第二种划分方式的计算出的Cl与Cd的值与实验结果相接近,可以认为第二种划分方式计算精度较高。

表1 Re=200时圆柱绕流数值计算结果与文献数据比较
3 结束语
通过以上分析,我们得出以下结论:
(1)对Re=200的低雷诺数圆柱舵杆绕流,采用层流模型并结合合理的网格划分,可以很好地模拟舵杆涡流运动,并通过对升力系数、阻力系数的分析,得到涡的脱落频率。
(2)虽然两种划分方式都可以模拟出圆柱舵杆绕流运动,但是第二种方法计算出的升力系数、阻力系数更加接近实验结果,因为,其在来流方向与垂直来流方向均加密了网格,较好的覆盖了圆柱舵杆的分离区域。
(3)本文只对静止的二维圆柱模型作了数值计算,未考虑圆柱的运动对流场产生的影响与三维模型的尺度效应。
[1]李 田,张继业,等.二维弹性圆柱涡致振动尾涡模态[J].空气动力学学报,2010,(06):25-26.
[2]顾 罡.二维圆柱绕流、双圆柱绕流问题和三维垂荡板运动的数值模拟[J].上海交通大学,2007,23-24.
[3]苑健康,黄维平.二维立管Helical Strakes绕流场的ANSYSCFD 分析[J].船海工程,2010,(04):26-27.
