Vondrak滤波在磁悬浮陀螺全站仪数据处理中的应用

李慧茹，杨志强，石 震，龚 云，赵敏宁

（长安大学 地质工程与测绘学院，陕西 西安 710054）

0 引 言

高精度磁悬浮陀螺全站仪是一种将磁悬浮技术成功应用于陀螺全站仪的精密定向测量仪器，它能够精确测定任意测线真北方位角，实现准确贯通和精确定向，通常用于地下工程，如大型隧道、矿山等的贯通测量工作，为地下工程提供精确的方位基准或相关的方位角检核条件［1－5］。然而，在实际施工现场，由于受到外界干扰力矩的影响，陀螺在寻北过程中旋转轴产生缓慢的偏北进动，陀螺采样数据往往包含系统性漂移和随机性漂移。系统性漂移可以通过试验标定或建立数学模型消除其影响，而随机性漂移具有弱非线性、非平稳、慢时变的特点，并且外界不确定干扰因素对随机性漂移的影响大小，无法建立其数学模型［6－7］，因此需要对陀螺采样数据进行适当的平滑处理来尽可能消除随机性漂移的影响，进而提高磁悬浮陀螺全站仪观测结果的精度。

对于陀螺随机性漂移的消除，已经有很多学者做了大量研究。李士心等对陀螺数据采用各种小波变换重构信号，进行滤波处理［6－8］；魏国等提出灰色时序建模新方法，并依据所建模型对激光陀螺数据进行Kalman滤波［9］；张通等采用粒子滤波方法对陀螺随机性漂移消噪［10］。笔者借助在天文数据处理中广泛应用的 Vondrak滤波法［11－12］对磁悬浮陀螺采样数据进行平滑处理，Vondrak滤波法不要求建立估计量与观测量之间的函数模型，而通过选择不同平滑因子控制数据的平滑程度对采样数据进行平滑处理，从而在最大程度上滤除随机误差或干扰成分，保留数据中的有用信息。

1 Vondrak滤波原理

对于采样数据，Vondrak滤波的基本假设是使Q取最小值，Q表达式为

其中

式中：yi为观测时刻xi的采样数据；i＝1，2，3，…，n，其中n为采样个数；yi－为待求的平滑值；pi为采样数据的权；F为Vondrak滤波的拟合度；S为平滑度；Δ3yi－为平滑值yi－的三阶差分；λ2为给定的正系数。

Vondrak滤波的思路是寻求一条折中的曲线，这条曲线介于采样数据的绝对平滑和绝对拟合之间，折中的程度取决于平滑因子ε＝1／λ2的选取［13］。在平滑过程中，λ2调整拟合度和平滑度之间的关系。当λ2→0，Q要取得最小值，则F取最小值，拟合曲线与采样数据逼近；当λ2→∞，要使Q取最小值，则S取最小值，这时得到的是一条光滑的二次曲线［13］。

Vondrak滤波采用相邻4组采样数据来构造一个三次拉格朗日多项式，并用此式表示中间的2个平滑值。首先将拉格朗日多项式代入式（2）、（3）得到F、S，具体多项式形式及推导过程详见文献［7］，然后对yi－求偏导，得到Vondrak滤波的基本方程组

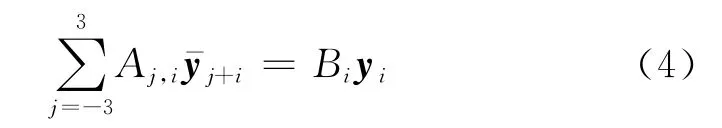
其中

Bi＝εpi

式中：Aj，i为矩阵的系数，j＝－3，－2，－1，0，1，2，3；y－

j＋i为第j＋i个采样数据的平滑值。

当j＋i≤0或j＋i≥（n＋1）时，Aj，i＝0。此时，Vondrak滤波转化为一个求解线性方程组的问题。只要平滑因子ε给定，就可以唯一地解算出一组平滑值。需要注意的是，平滑因子ε选取不同的值，可以得到不同程度的平滑结果，ε取值偏小，所得结果的平滑度强，ε取值偏大，所得结果的平滑度弱。在本文数据处理中，由于数据采样量大，并且陀螺全站仪在不受外力干扰的作用下几乎是一个常数，所以平滑因子选取应该偏小。经过观测误差法比较分析，本文平滑因子取ε＝0．01。

2 应用实例

磁悬浮陀螺全站仪通过2次寻北观测数据（即第1位置寻北力矩和第2位置寻北力矩）计算真北方位角。笔者在西安地区选取一条基准线，并采用高精度天文测量方法获取其真北方位角，然后在这条基准线上进行陀螺方位角测量试验，共反复进行8次测回，每一测回共有40 000组第1位置寻北力矩值和第2位置寻北力矩值。在计算真北方位角之前，首先利用Vondrak滤波法对这8次测回的数据进行平滑处理。图1、2为第1测回原始采集的第1、2位置寻北力矩值与Vondrak滤波处理后的第1、2位置寻北力矩值的比较图。第2～8测回原始采集的寻北力矩数据与Vondrak滤波处理后的寻北力矩数据的结果与图1、2相似，因此文中不再重复。

Vondrak滤波平滑的目的是尽可能消除磁悬浮陀螺全站仪随机性漂移的影响。在图1中第1位置寻北力矩平滑处理前，纵坐标区间为［－0．02，0．02］，平滑处理后减小到［－0．01，0．01］，反映出 Vondrak滤波能够有效消除磁悬浮陀螺全站仪的随机性漂移影响。从图1、2可以看出，Vondrak滤波平滑处理结果能够反映磁悬浮陀螺全站仪寻北力矩的变化趋势，平滑后的结果与原始数据相比，数据序列的毛刺减少，数据更为集中。但是从图1、2也可以看出，对于原始采集的第1、2位置寻北力矩，共有3处大的起伏波动，这是因为在试验时测量环境受到噪音等外界干扰因素造成的，这些波动属于粗差范围，在计算真北方位角时应该予以剔除，在进行Vondrak滤波处理之后这些波动仍然存在，因此使用Vondrak滤波平滑处理时应考虑结合粗差剔除进行数据处理。

从图1、2中可以直观看出，Vondrak滤波能够滤除磁悬浮陀螺全站仪数据的干扰成分，保留有用信息。同时，笔者通过计算寻北力矩的均方根对磁悬浮陀螺全站仪原始采集数据和Vondrak滤波平滑处理结果进行比较。从表1可以看出，8次测回Vondrak滤波平滑处理数据与对应的原始采集数据相比，它的所有均方根都明显减小，说明Vondrak滤波平滑处理后寻北力矩离散度变小，数据变得更集中。Vondrak滤波有效消除了数据的随机性漂移影响，计算真北方位角时精度得到提高。

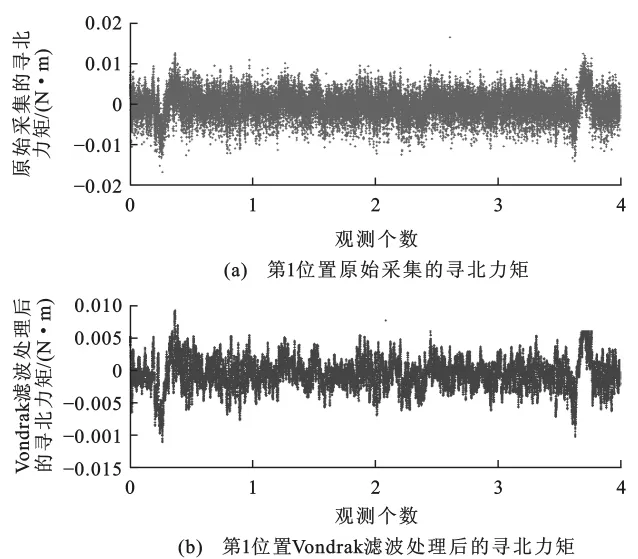
图1 第1测回的第1位置原始寻北力矩数据与Vondrak滤波处理数据比较Fig．1 Comparison of Raw Data of North－seeking Torque in the First Place of the First Observation Set and Data Processed by Vondrak Filter

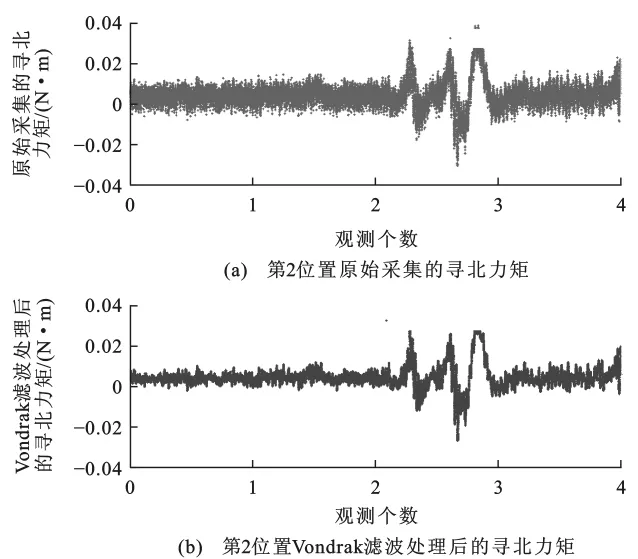
图2 第1测回的第2位置原始寻北力矩数据与Vondrak滤波处理数据比较Fig．2 Comparison of Raw Data of North－seeking Torque in the Second Place of the First Observation Set and Data Processed by Vondrak Filter

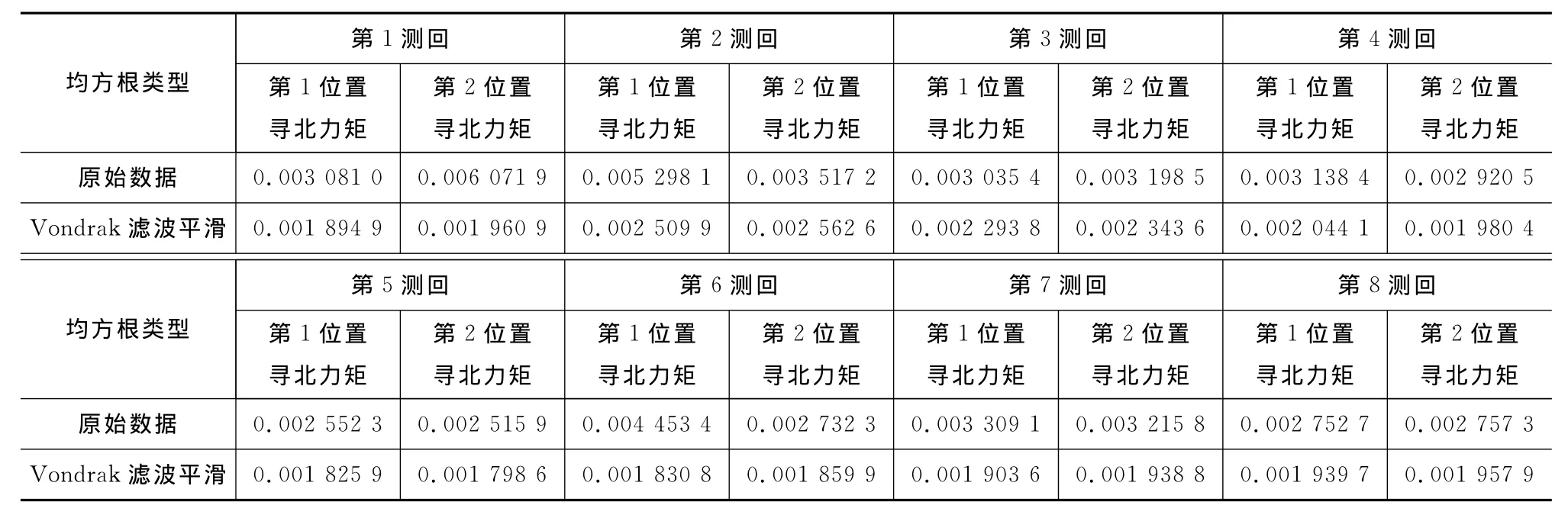
表1 原始采集数据和Vondrak滤波平滑处理结果的均方根比较Tab．1 Comparison of Root Mean Squares Between Raw Data and Results Smoothed by Vondrak Filter N·m

3 结 语

（1）Vondrak滤波平滑处理后的结果能够消除磁悬浮陀螺全站仪的随机性漂移影响，反映寻北力矩的变化趋势，平滑处理结果的均方根得到改善。

（2）由于Vondrak滤波不能剔除粗差，因此利用Vondrak滤波处理磁悬浮陀螺全站仪采样数据时，应该结合粗差剔除同时使用，这样才能使最终的真北方位角精度得到较大提高，而寻找高效的粗差剔除方法也是下一步的研究重点。

（3）在采用Vondrak滤波时，应根据实际情况选取合理的平滑因子。

［1］ 杨建华．GAT磁悬浮陀螺全站仪自动化与陀螺仪观测数据分析［D］．西安：长安大学，2010．YANG Jian－hua．Automation of the GAT Magnet Suspended Gyro－total－station and the Gyroscope's Data Analysis［D］．Xi'an：Chang'an University，2010．

［2］ 王新龙，李 娜．MEMS陀螺随机误差的建模与分析［J］．北京航空航天大学学报，2012，38（2）：170－174．WANG Xin－long，LI Na．Error Modeling and Analysis for Random Drift of MEMS Gyroscopes［J］．Journal of Beijing University of Aeronautics and Astronautics，2012，38（2）：170－174．

［3］ 崔 铭．粒子滤波在MEMS陀螺仪初始对准中的应用［J］．传感技术学报，2011，24（9）：1275－1278．CUI Ming．The Usage of Particle Filtering Algorithm in Initial Alignment of MEMS Gyro［J］．Chinese Journal of Sensors and Actuators，2011，24（9）：1275－1278．

［4］ 钱华明，夏全喜，阙兴涛，等．基于 Kalman滤波的MEMS陀螺仪滤波算法［J］．哈尔滨工程大学学报，2010，31（9）：1217－1221．QIAN Hua－ming，XIA Quan－xi，QUE Xing－tao，et al．Algorithm for a MEMS Gyroscope Based on Kalman Filter［J］．Journal of Harbin Engineering University，2010，31（9）：1217－1221．

［5］ 袁赣南，梁海波，何昆鹏，等．MEMS陀螺随机性漂移在线补偿技术［J］．北京航空航天大学学报，2010，36（12）：1448－1452．YUAN Gan－nan，LIANG Hai－bo，HE Kun－peng，et al．On－line Compensation Technique for Micromechanical Gyroscope Random Error［J］．Journal of Beijing University of Aeronautics and Astronautics，2010，36（12）：1448－1452．

［6］ 李士心，刘鲁源，杨 晔，等．基于平稳小波变换的陀螺仪信号去噪方法［J］．天津大学学报，2003，36（2）：165－168．LI Shi－xin，LIU Lu－yuan，YANG Ye，et al．Gyro Signal Denoising Using Stationary Wavelet Transform［J］．Journal of Tianjin University，2003，36（2）：165－168．

［7］ 万彦辉，秦永元．小波分析在陀螺信号滤波中的研究［J］．压电与声光，2005，27（4）：455－457．WAN Yan－hui，QIN Yong－yuan．Application of Wavelet Analysis in Gyro Signal Filtering［J］．Piezoelectrics and Acoustooptics，2005，27（4）：455－457．

［8］ 张 通，张 骏，张 怡．基于改进小波阈值的激光陀螺漂移信号降噪［J］．仪器仪表学报，2011，32（2）：258－263．ZHANG Tong，ZHANG Jun，ZHANG Yi．Ring Laser Gyro Drift Signal Denoising Based on Improved Wavelet Threshold［J］．Chinese Journal of Scientific Instrument，2011，32（2）：258－263．

［9］ 魏 国，汤建勋，王 宇，等．基于灰色时序模型的激光陀螺漂移数据滤波［J］．红外与激光工程，2011，40（4）：747－751．WEI Guo，TANG Jian－xun，WANG Yu，et al．Filtering of RLG's Drift Data Based on Grey－time Series Model［J］．Infrared and Laser Engineering，2011，40（4）：747－751．

［10］ 张 通，张 骏，郑梦兴．基于粒子滤波的陀螺随机性漂移预测模型研究［J］．仪器仪表学报，2010，31（5）：1190－1193．ZHANG Tong，ZHANG Jun，ZHENG Meng－xing．Partical Filter Based on Modeling Research for Gyroscope Random Drift［J］．Chinese Journal of Scientific Instrument，2010，31（5）：1190－1193．

［11］ 聂士忠．Vondrak数据平滑方法及其在微机上的实现［J］．石油大学学报：自然科学版，1994，18（4）：111－114．NIE Shi－zhong．Vondrak Data Smoothing Method and It's Application with a Microcomputer［J］．Journal of the University of Petroleum，China：Natural Science Edition，1994，18（4）：111－114．

［12］ 孙 亮．Vondrak数据平滑方法在放射性药物生物动力学数据处理中的应用［J］．核技术，2004，27（8）：604－607．SUN Liang．Application of Vondrak Smoothing Method for Pretreatment of Biokinetic Data of Radiopharmaceuticals［J］．Nuclear Techniques，2004，27（8）：604－607．

［13］ 李 变．利用Vondrak方法处理GPS CV观测数据的随机噪声［J］．计算机测量与控制，2006，14（7）：953－954．LI Bian．Filtering Random Noise from GPS CV Observed Data with Vondrak Method［J］．Computer Measurement and Control，2006，14（7）：953－954．

［第34卷卷终］