桥梁高墩地震反应中高阶振型贡献程度的分析

卢 皓， 李建中

(同济大学 桥梁工程系，上海 200092)

0 引言

跨越山谷的高墩桥梁在我国的铁路和公路建设中被广泛使用，例如宜万铁路渡口河特大桥的最高墩128 m，黄延高速公路的洛河特大桥最高墩达143 m。《公路桥梁抗震设计细则(JTG/T B02-01—2008)》指出对于墩高超过40 m，墩身第一阶振型有效质量低于60%，且结构进入塑性的高墩桥梁应作专项研究［1］，美国CALTRANS 抗震设计规范仅适用于规则桥梁，而高墩桥梁一般都是典型的非规则桥梁［2］。

近年来，国内外学者对高墩桥梁的抗震性能进行了很多研究，李建中、宋晓东指出采用传统的只考虑一阶振型的pushover 方法分析高墩抗震性能会产生很大的误差［3］;梁智垚通过增量动力分析方法即:Incremental Dynamic Analysis (IDA)方法，计算了非规则桥梁中的不同墩高墩柱的屈服位移、极限位移和位移延性能力，讨论了墩身质量和高阶振型参与对高墩墩身节点位移、截面曲率的影响［4］;Rosario Ceravolo等研究了高墩抗震设计中使用能力设计方法时应考虑的塑性铰位置，并探讨了地震动的频谱特性本身对高墩抗震设计的影响［5］;高墩具有截面尺寸大、结构周期长、墩身质量大等特点，并且地震动输入的频谱特性本身就会影响高阶振型的贡献程度，因此本文以不同墩高的典型山区桥梁墩柱为研究对象，通过对每级地震作用下对应墩底曲率达到最大时刻的结构刚度进行模态分析，进而研究在地震反应下高阶振型贡献程度。

1 增量动力分析

增量动力分析(IDA)是一种动力参数分析方法，它是将地震动的加速度分别乘以一系列加速度调整系数，使之成为一组不同强度的地震动，结构在这组地震荷载作用下，分别进行非线性动力时程分析，通过绘制所研究结构性能参数与加速度调整系数的IDA 曲线，对结构的整个损伤、破坏过程进行研究，该方法能够考虑高阶振型对桥墩抗震性能的影响。

对高墩进行抗震分析时，在整个非线性过程中，主要关注的两个状态是等效屈服状态和极限状态，这

按照墩底曲率进行判断。根据《公路桥梁抗震设计细则(JTG/T B02-01—2008)》条文7．4．4 条将实际的墩底截面轴力-弯距-曲率曲线按能量等效的原则确定等效屈服曲率［1］，极限曲率是受拉的纵向钢筋应变达到折减极限拉应变时对应的墩底曲率φu。

采用IDA 方法对高墩进行抗震性能的分析能够研究高墩结构在地震动作用下从弹性到屈服再到极限的整个过程。将高墩在某级地震动作用下墩底曲率达到屈服状态和极限状态时刻的墩顶位移分别称为“等效屈服位移”、“极限位移”。后面提到的屈服即为等效屈服。

2 瞬时模态分析

在弹性范围内对结构刚度进行模态分析得到的各阶周期、各阶振型向量、以及振型参与系数和质量参与系数通常是不变的，然而当结构在地震作用下进入塑性阶段后，每时刻的周期都在发生变化，可以通过对每级地震作用下对应墩底曲率达到最大时刻的结构刚度进行模态分析，就能得到结构在该时刻的瞬时周期、瞬时振型、以及对应的瞬时振型参与系数、瞬时质量参与系数以及瞬时周期对应的延性位移谱坐标。

结构在地震作用下墩底曲率达到最大时刻t 的瞬时振型参与系数为

结构在地震作用下墩底曲率达到最大时刻t 的瞬时质量参与系数~M 为

3 高阶振型对位移贡献程度的评估

一般对弹性结构振型贡献程度的衡量指标有振型参与系数、质量参与系数、以及Chopra 提出的振型贡献系数指标［6］。但上述指标都无法考虑地震动特性对振型贡献的影响。主要研究高阶振型对墩身位移的贡献程度，由于高阶振型的贡献程度会随着结构塑性程度的不同而发生变化，为了研究高墩在地震作用下高阶振型对墩身位移的贡献程度，在瞬时模态分析的基础上，提出比值~R 来衡量高阶振型对位移的贡献，这里只研究前两阶。

式中，Sd，j为对应某级地震动作用下墩底曲率达到最大值的时刻t 的第j 阶瞬时周期对应的延性位移谱值。

4 算例

4．1 计算模型及分析软件

计算模型采用大量典型山区高墩桥梁为原型并进行适当简化，墩柱计算模型采用墩底固结的悬臂梁，墩身质量堆聚在相应的节点上，将与墩柱相邻的一跨上部结构质量等效为墩顶集中质量。将模型的基本参数列在表1 中。

表1 墩柱基本参数

非线性时程动力分析采用美国太平洋地震工程研究中心开发的OpenSees 地震分析软件［7］。计算模型中墩柱采用弹塑性梁柱(纤维单元)模拟，桥墩截面划分为600 个纤维单元，混凝土纤维的应力-应变关系采用Mander 模型［8］，钢筋的应力-应变关系采用理想弹塑性应力-应变关系。混凝土结构的阻尼比取为5%，采用瑞利阻尼。进行增量动力分析时，从美国太平洋地震工程中心的强震数据库中选取El Centro 波的N-S 分量进行分析。在确定各阶周期对应的位移谱值时采用Chopra 建议的延性反应谱［6］。

4．2 计算结果及分析

4．2．1 IDA 分析

通过对墩底纤维截面进行轴力-弯矩-曲率的分析，得到墩底截面在达到等效屈服状态和极限状态对应的曲率，将不同墩高模型对应屈服状态和极限状态的墩底曲率值列在表2 中。

表2 屈服状态和极限状态的墩底曲率值 m －1

通过IDA 分析，能够得到高墩在El Centro 地震波作用下达到等效屈服状态、极限状态的对应时刻的位移分布，如图1 所示。

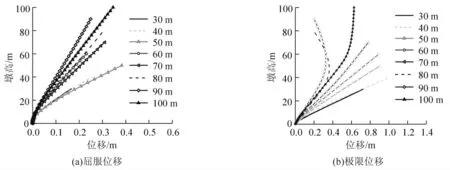
图1 位移分布

由图1 可看到墩身屈服状态的位移分布中高阶振型的参与程度并不高，而极限状态的位移分布图中可以看到80 m、90 m、100 m 桥墩的位移明显出现了高阶振型的形状。

4．2．2 瞬时模态分析

在IDA 分析过程中对每级地震动作用下对应墩底曲率达到最大时刻的结构刚度进行记录，对这些时刻的结构刚度进行模态分析可以得到各阶振型特征向量，然后按照墩顶振型为1 进行正规化，将非线性过程中的4 个状态下的前两阶正规化的振型绘制在图2 和图3 中，图中A、B、C、D4 个状态分别对应PGA为0．1g 地震作用、墩底达到等效屈服状态、PGA 为1g 地震作用、墩底达到极限状态。

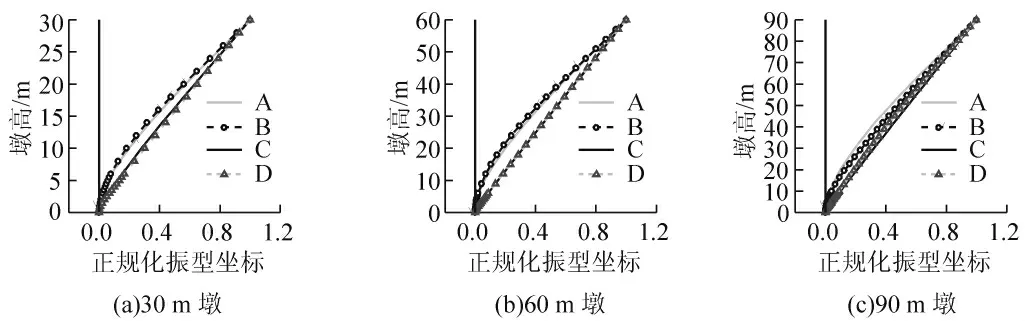
图2 瞬时一阶振型

通过观察图2 和图3，可以看到30 m、60 m 以及90 m 一阶振型的变化趋势基本一致，二阶振型在墩身中部位置的变化较大。

在IDA 分析过程中对每级地震动作用下对应墩底曲率达到最大时刻的结构刚度进行记录，对这些时刻的结构刚度进行模态分析可以得到各阶瞬时振型参与系数和瞬时质量参与系数，本文选取了8 级地震动的结果，将8 级地震动作用下墩底达到不同曲率的瞬时振型参与系数和瞬时质量参与系数作为研究样本，按照公式计算标准差，将结果绘制在图4 中。

图3 二阶振型

图4 标准差

从图5 中可以看到前两阶瞬时振型参与系数的标准差很小，一阶瞬时振型参与系数中60 m 墩的标准差最大，为0．005 1;二阶瞬时振型参与系数中90 m、100 m 墩的标准差最大，为0．006 1。而前两阶瞬时质量参与系数的标准差也很小，一阶瞬时质量参与系数中100 m 墩的标准差最大，为0．037 7;二阶瞬时质量参与系数中100 m 墩的标准差最大，为0．017 85。由此可知，桥墩在地震动作用下的整个非线性过程中，振型参与系数和质量参与系数在不同时刻的变化很小。

在IDA 分析过程中对每级地震动作用下对应墩底曲率达到最大时刻的结构刚度进行记录，对这些时刻的结构刚度进行模态分析可以得到对应各阶瞬时周期的延性位移谱值。将前两阶瞬时周期对应的延性位移谱值绘制在图5 中。可以看到随着墩底曲率的增加，各高墩模型的一阶瞬时周期对应的延性位移谱值增加的趋势基本一致，只有90 m 墩在屈服后的位移谱值增长较快。而随着墩底曲率增加，各高墩模型的二阶瞬时周期对应的延性位移谱值的增加趋势有很大不同，其中30 ～60 m 的谱值增加较慢，而70 ～100 m 增加较快，尤其是80 m 和90 m 墩高模型的谱值增加幅度最大。

4．2．3 高阶振型对位移贡献程度

为了研究高墩在地震作用下高阶振型对墩身位移的贡献程度，在瞬时模态分析的基础上，提出比值~R来衡量高阶振型对位移的贡献，这里只研究前两阶。将瞬时模态分析得到的前两阶墩顶、墩身中部瞬时振型(按照墩顶为1 进行正规化)和瞬时周期对应的延性位移谱值代入公式(3)中，将计算得到的墩顶位置和墩身中部位置的~R 比值列在图6 中。

图5 瞬时延性位移谱值

图6 比值R

从图6 中可看到，不同墩高模型的墩顶位置和墩身中部位置的比值~R 随着墩底曲率的增加而呈现出不同的趋势，其中30 ～60 m 墩的增加趋势很小，而70 ～100 m 墩的增加趋势很明显，尤其是80 m 和90 m墩的增加趋势最为明显。当桥墩在地震作用下墩底达到极限状态的曲率时，30 m、40 m、50 m 桥墩的墩顶位置的比值~R 分别为0．002、0．01、0．01;60 m、70 m 桥墩的墩顶位置的比值~R 分别为0．03、0．06;而80 m、90 m、100 m 桥墩模型的墩顶位置的比值~R 都超过了0．15，可以看到80 m、90 m、100 m 桥墩在El Centro波作用下高阶振型对于墩顶位移的贡献程度是相当高的。

5 结论

(1)通过对不同墩高的典型山区桥梁高墩进行IDA 分析，可知在El Centro 波的N-S 分量作用下80 m、90 m 以及100 m 墩高的桥墩模型在极限状态时的位移分布呈现出高阶振型参与程度较高的形状。

(2)在IDA 分析过程中对每级地震动作用下对应墩底曲率达到最大时刻的结构刚度进行记录，对这些时刻的结构刚度进行模态分析能够得到各阶振型特征向量，通过分析可知，前两阶振型随着非线性程度的增加，出现不同程度的变化，30 m、60 m、90 m 墩高模型的一阶振型变化趋势基本一致，而二阶振型在墩身中部位置的变化程度较大。

(3)通过瞬时模态分析可知，在不同地震动水平作用下墩底曲率达到最大时刻的瞬时振型参与系数和瞬时质量参与系数变化并不大。

(4)通过记录El Centro 波不同地震动水平作用下墩底曲率达到最大时刻的瞬时周期，绘制对应瞬时周期的延性反应谱值随着墩底曲率变化的趋势图，可以知道各高墩模型的一阶瞬时周期对应的延性位移谱值增加的趋势基本一致，而随着墩底曲率增加，各高墩模型的二阶瞬时周期对应的延性位移谱值的增加趋势有很大不同。

(5)瞬时模态分析的基础上，通过比值~R 来衡量高阶振型对位移的贡献，可以看到80 m、90 m、100 m桥墩在El Centro 波作用下高阶振型对于墩顶位移的贡献程度是相当高的。

［1］重庆交通科研设计院． JTG/T B02-01—2008 公路桥梁抗震设计细则［S］．北京:人民交通出版社，2008．

［2］California Department of Transportation． Caltrans Seismic Design Criteria Version 1．5［S］．State of California:Business Transportation and Housing Agency，2009．

［3］李建中，宋晓东，范立础．桥梁高墩位移延性能力的探讨［J］．地震工程与工程振动，2005，25(1):43-48．［4］梁智垚． 非规则高墩桥梁抗震设计理论研究［D］．上海:同济大学土木工程学院，2007．

［5］Rosario Ceravolo，Giacomo Vincenzo Demarie ，Luca Giordano，Giuseppe Mancini，Donato Sabia． Problems in applying codespecified capacity design procedures to seismic design of tall piers［J］． Engineering Structures，2009，31:1811-1821．

［6］Anil K Chopra． Dynamics of structures:theory and applications to earthquake engineering［M］． New Jersey:Prentice Hall，Inc，2001．

［7］Silvia Mazzoni，Frank McKenna，Michael H． Open system for earthquake engineering simulation user manual［M］． Berkeley:Pacific Earthquake Engineering Research Center，University of California，2007．

［8］Mander J B，Priestly M J N，Park R． Theoretical stress-strain model for confined concrete［J］． Journal of Structural Engineer，ASCE，1988，114(8):1806-1826．