MEMS加速度计静态温度模型的辨识
2012-02-15夏克洪
夏克洪,米 亮
(1.四川九洲电器集团有限公司 四川 绵阳 621000;2.重庆邮电大学 重庆 400065)
随着微机电系统(MEMS)技术的发展,以及微加速度计的商业和军事价值的提高,微加速度计成为微机电系统领域和微传感器领域内研究热点[1]。MEMS加速度计的精度受到制造工艺、内部结构等影响,同时也与工作环境条件(如温度、湿度、空气压力等因素)有关[2]。其中,温度变化对加速度计性能影响较大。目前为了降低温度影响的方法主要有以下4种:1)研制对温度不敏感的惯性器件。从惯性器件热设计出发,使惯性器件的布局、零件的材料和结构形状,满足对温度不敏感的要求;2)在结构中增加特定温度系数的材料、元件,以抵消温度变化引起的另外有关组件的材料物理参数的变化,补偿温度对惯性器件精度的影响;3)尽可能地改善测试环境温度,或采用一定的硬件措施使惯性器件工作环境温度恒定;4)研究惯性器件静、动态温度模型,计算出相应的附加误差,进行实时补偿。前3种方法都是基于硬件补偿的思想,即通过改变结构、材料、工艺和工作环境等方法来提高惯性器件的精度。第4种方法是基于软补偿的思想,即通过测试进行误差分离与补偿。可以建立加速度计的数学模型,用于补偿当环境因素改变时,加速度计产生的误差。研究环境条件对加速度计数学模型影响的规律,是提高加速度计使用精度的重要手段。文中针对某一加速度计进行全温实验,考虑到工程实际,讨论采用静态温度建模的方法对系统中的微机械加速度计进行温度补偿。
1 MEMS加速度计标定技术
1.1 现有标定技术及存在的问题
文献[3]采用的辨识方法是在各设定的温度点下,采集温度传感器和微机械加速度计的输出值,根据温度测量值求出加速度计零位和标度因数,解算出多位置平均温度下加速度计零位和标度因数,分别采用最小二乘法和多项式拟和对各系数拟合,进而拟合得到零位和比例因子的温度模型,建立微机械加速度计静态温度模型。
然而在实际的高低温实验中,多位置实验过程中温度变化很快,这样根据多个位置的平均温度来解算出的零位和比例因子本身就有很大误差,而这一误差也带进了温度模型。这样误差势必会带来较大的模型误差,其结果有时甚至会恰得起反,还不如不补偿温度误差[4]。另外,温度试验标定的零位和标度因数的温度模型呈一定的非线性,很难建立合适的、准确的温度误差模型,尤其是标度因数。
1.2 加速度计标定模型
深入研究影响MEMS加速度计静态模型的因素,进一步改善其标定方法,对于提高MEMS加速度计的性能有着很好的工程实用价值。文中采用零偏和标度因数同时补偿的思想,得到了MEMS加速度计静态温度模型系数随温度变化的规律,采用逐步回归分析的方法,在不同温度段将加速度计建模为以输出电压V、器件温度T、器件温度变化率、环境温度、环境温度变化率为输入、加速度测量误差为加速度计输出的分段模型,则加速度测量误差为加速度计输出电压和温度的函数 a=f (V,T,ΔT,T o,ΔT o), 其中 ΔT 为器件温度变化率,T o为环境温度,ΔT o为环境温度变化率。
2 标定实验
为了辨识加速度计静态温度模型,首先要进行在各温度点下的静态试验。将MEMS加速度计放入高低温箱冷冻后,在大理石平板上进行加速度计位置实验。标定软件用VC++6.0编写,多线程通讯,可显示及自动记录数据。试验时设定的温度范围为-40~60°C,试验所采用的高低温箱其温度控制、测量精度均为±1°C,正常情况下,升、降温速度约1°C/1 min,但温度低于-20°C 时,降温非常慢,约-1°C/7 min。 将加速度计固定于温控箱内,从室温(约20°C)加热到60°C,保温10 min,再减温到-45 °C,保温 15 min,再加温到 60 °C,保温10 min,过程如此循环反复几次。
3 加速度计温度模型
环境温度对加速度计影响较大,要进行必要的补偿。文中提出一个基本模型,加速度计测量误差为输出电压V、器件温度T、器件温度变化率、环境温度、环境温度变化率的函数,即转化为多因素回归问题。而为了减少测量误差的影响,可以采用逐步线性回归,得到简化的加速度计模型[5]。
温度误差模型中温度T和输出电压V最高都取二阶,则MEMS加速度计多因素回归模型有21个因素。进行逐步回归分析进行优化,则多因素回归模型中得到加速度计的分段简化模型(以Z轴为例),得加速度计温度补偿模型:

建模结果如图1所示,加速度计误差在3 mg以内,比传统方法有更高的模型精度。

图1 加速度计建模误差随温度变化曲线Fig.1 Accelerometer modeling error changing with temperature curve
4 加速度计模型辨识结果
行判别。一般用单个自由度的回归平方和(回归均方和)与单个自由度的误差平方和(误差均方和)之比值作为判别模型方程显著性的依据。由于这一比值是符合于概率统计中的F分布规律,可以用F统计量来检验,根据试验中所取得的数据,可以计算出。

其中Q为误差平方和,F值越大,模型方程越显著。如果F值接近1,说明系统误差和随机误差两级相近,模型方程就没有什么实际意义[6]。
因为温度试验进行了21次,所以n=21,由于偏差平方和S中有平均值的约束,其自由度为n-1=20,当加速度计温度误差分段模型方程中的自变量k=7时,即输入的改变有k个机会时,因此u的自由度应为k,根据自由度保持不变的原理,因此误差平方和Q的自由度为n-k-1=13。再根据温度误差标定试验的实际情况,设定显著水平α=0.9,可以很方便地计算出各个加速度计温度误差模型的F值,然后通过F分布表查到的规定值。
按上述方法,计算模型的F值,结果列入表1中,可以看到优化的模型的F计算值都大于F分布表规定值,所以显著水平α=0.9下,加速度计分段优化模型是显著的。

表1 温度误差模型显著性检验Tab.1 Temperature error model significant inspection
由上述F值可以看出,均大于1,分段优化模型是显著的。为了验证补偿后得到的模型的有效性,对补偿后的MEMS加速度计进行了测试。试验记录的结果如图2所示,补偿后的加速度计测量精度有了很大的提高。经过补偿后的加速度计在全温范围内误差保持在5 mg以内。
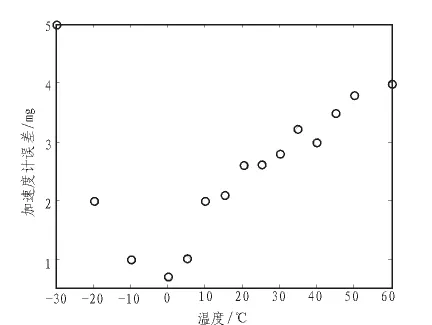
图2 加速度计补偿后静止时的误差Fig.2 Accelerometer static error compensation
为了提高模型的可信度,一般需要对模型方程显著性进
5 结 论
文中针对某一加速度计进行了全温度范围的精确标定,将零位和标度因数统一标定,加速度计建模为以输出电压V、器件温度T、器件温度变化率、环境温度、环境温度变化率为输入、加速度测量误差为输出,并采用逐步线性回归得到了简化的分段模型。实验验证表明,此方法在很大程度上降低了加速度计的静态误差,实现了加速度计精确标定,补偿了非线性误差,提高了MEMS加速度计全温度范围内的性能,具有很好的工程实际应用价值。
[1]刘云涛,王颖,邵雷.改进的电容式微加速度计中电路噪声模型[J].哈尔滨工程大学学报,2012,33(4):1-5.LIU Yun-tao,WANG Ying,SHAO Lei.Improved capacitive micro accelerometers circuit noise model[J].Journal of Harbin Engineering University,2012,33(4):1-5.
[2]黄贤武,郑莜霞.传感器原理与应用[M].成都:电子科技大学出版社,1999.
[3]Michael A H,Jose A R,Jin S.6421622.Dynamic attitude measurement sensor and method[S].US,2002.
[4]李国辉,戴世荣,杨孟兴.加速度计静态温度模型的辨识[J].导航与控制,2007,15(1):1-4.LI Guo-hui,DAI Shi-rong,YANG Meng-xing.Accelerometer static temperature model identification[J].Navigation and control,2007,15(1):1-4.
[5]郭鹏飞,任章,杨云春.一种低精度惯性测量单元的精确标定技术[J].中国惯性技术学报,2004,15(1):1-4.GUOPeng-fei,RENZhang,YANGYun-chun.A low precision inertia measurement unit precision calibration technique[J].Chinese Journal of Inertial Technology,2004, 15(1):1-4.
[6]王成.MEMS惯性器件参数辨识及误差补偿技术[D].哈尔滨:哈尔滨工程大学,2006.
