基于分层模型的输电线路选线算法设计
2012-02-13康健民袁敬中肖少辉赵俊生刘震
康健民,袁敬中,肖少辉,赵俊生,刘震
(1.华北电网有限公司,北京市,100053;2.北京洛斯达科技发展有限公司,北京市,100120;3.武汉大学,武汉市,430072)
0 引言
输电线路的路径选择是电网建设的前提,其设计的合理性影响着线路投资运行成本的大小与运行的可靠性。输电线路的选择要求选线人员要综合考虑地形、地貌、地质、交通、环境以及各地、各部门的政策法规等多方面的因素。为了降低选线的难度,减轻选线人员的工作量,节省选线的时间及成本,利用计算机来选择输电线路成为电力设计人员和相关研究学者关注的目标。
国外在20世纪90年代就开始了这方面的研究,文献[1]使用卫星影像来确定影像因素,并赋予一定权重,选出一条代价最小的路径;文献[2]研究了城区里输电线路的自动选线方法;文献[3-4]将地理信息系统中栅格结构的思想引入输电线路的线路规划中,选择输电线路;文献[5-7]也在栅格数据的基础上进行了选线的研究;文献[8]提出了SPI方法以解决公共参与对线路选择的不良影响;文献[9]利用空间建模方法通过人工干预得到初选路径,以此确定合理的布线走廊。然而,上述方法都是将所有数据、影响因子放在1个层次中考虑,没有注意到由于不同区域的地形复杂度、地物不同,其影响因子也不同,这样既影响选线的准确性,也会降低选线的速度。
基于以上问题,华北电网有限公司根据多年选线经验,组织各方面专家讨论研究,将人工选线过程中先粗选后细选的思想和动态导航中分层搜索的思想[10]运用到选线算法中,提出由粗到细、分层次、逐级运算的算法,同时在数据组织方面采用了将地理数据以栅格格网表示的思想,进行计算机智能选线研究。经过试验分析表明,采用该算法不仅选择的线路符合要求,而且其选线速度快于其他方法。
1 数据模型设计与影响因子分析
1.1 数据模型设计
由于矢量数据结构不能很好地表示地形信息(坡度、限制区等)[3],因此在电力选线中大都采用栅格数据模型[3-9]。栅格数据模型是由多个规则的网格单元组成,将要进行选线的区域按一定规则进行划分,形成相互连接的规则多边形,每个多边形称为网格单元,每个网格单元都存储经过此单元所花费的成本。可以对选线区域进行多种格网等级的划分,网格单元越小,选出的路径越具体,但花费的时间越多;从较大的网格单元中选出一条路径花费的时间较少,但很多影响因子无法得到合理利用,所选路径较为粗略、准确性差,无法应用到实际当中。
目前的栅格数据模型都是在1个尺度的网格单元上进行选线,无法兼顾选线时间长短和线路的准确性问题。为了解决这个问题,本文设计了多层次的数据模型,不同层次存放不同大小的格网单元。这样在线路选择时就能先在格网单元较大的层选出一条粗略路径,然后在包括该粗略路径覆盖范围的下一层内选出一条较细的路径,直至选到最小的格网单元层,如图1所示,图1中包含斜线的网格为路径经过的网格单元。
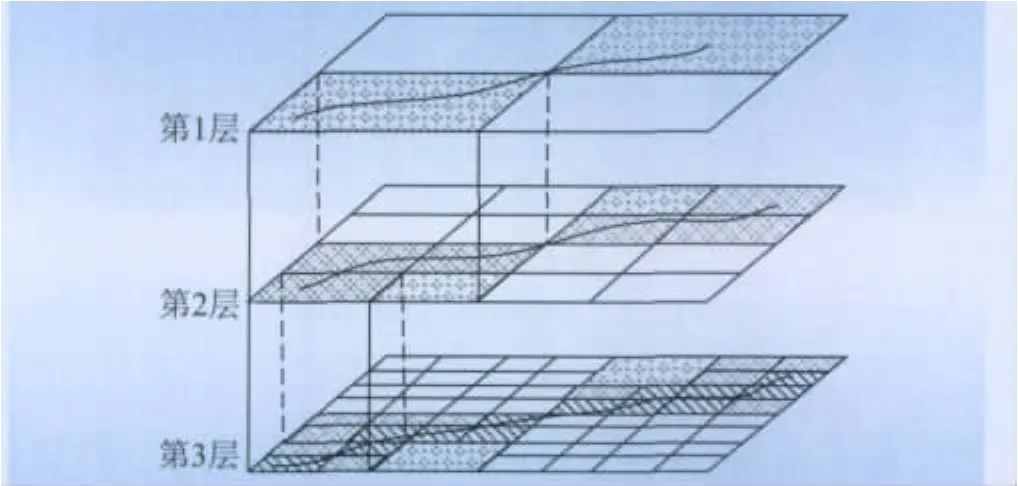
图1 栅格数据模型及选线Fig.1 Raster data model and route selection
1.2 影响因子分析
输电线路经过的地域范围较广,会遇到多种地形地貌,比如山地、不良地质带、公路、河流、居民地、自然保护区等。如何划分这些因素,并将这些因素量化为计算机能够识别的形式是进行选线的前提。本文将影响因素分为以下4类:
(1)社会因素。社会因素主要包括禁止通过区和协商通过区。禁止通过区是指输电线路不能穿过的区域,包括军事区、大型工矿企业、易燃易爆物品聚集处、自然保护区的核心区等。该区域的成本值记为M=∞。协商通过区是指一些应尽量避免但却无法避免穿过的区域,通过这种区域一般需要较高的成本,包括居民地、不良地质带和露天矿场、重冰区、河流湖泊等,通过该区域的成本值记为C。
(2)自然因素。自然因素主要考虑地形方面对选线的影响,包括坡度和高程2个方面。坡度所造成的成本值记为S,高程造成的成本值记为H。
(3)经济因素。在选取2地输电线路时,应在考虑到其他因素的情况下保证线路最短,2个网格之间的距离成本记为D(g1,g2)。输电线路的转角塔的成本都比较高,线路应尽量避免方向的改变,转角成本记为 D(g0,g1,g2)。
(4)交通因素。为方便施工及维护,所选线路应尽量靠近交通设施。由于高速公路及铁路作为主干路,为避免电线对其造成影响,当交叉时以接近90°为宜;一般公路可以不考虑交叉角。运输成本记为T。
2 算法设计
基于人工选线中的流程和动态导航中为解决运算时间所采取的方法,本文提出一种基于分层模型的输电线路选线算法。该算法考虑了3个层次L1、L2、L3,3个层次的网格单元大小递减:G(L1)>G(L2)>G(L3)。该算法在不同的层次考虑了不同的影响因子,具体过程为:调用第1个层次的网格和各影响因子对应的数据进行叠加分析,生成成本格网,然后调用最短路径算法选出通道,在通道的覆盖区域调用下一层次格网,直至选出一条优化路径。在相同的层次,不同的影响因子对选线的影响不同,要赋予相应的成本。在不同的层次,相同的影响因子对选线的作用也可能不同,因此也需要根据层次的不同改变该影响因子的成本。
在对成本格网进行运算时,网格gk-1和到相邻格gk的成本值称为可达性成本值,用F(gk-1,gk)表示。由于不同的层次考虑的影响因子不同,可达性成本值在不同层次的计算式也就不同,分别由式(2)、(6)、(9)计算。每个网格单元都有8个相邻格网(U={gN,gNE,gE,gSE,gS,gSW,gW,gNW}),网格 gk∈∞ 到起始网格gorigin的成本值用W(gorign,gk)表示。
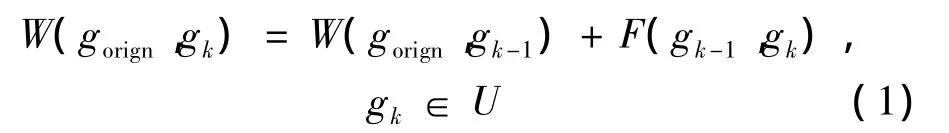
(1)在L1层需考虑距离因素。gk-1到gk的可达性成本值由式(2)计算。(Xk,Yk)、(Xk-1,Yk-1)分别为gk、gk-1的地理位置,C(gk-1)和 C(gk)分别为协商区中gk-1和gk所占的成本值。
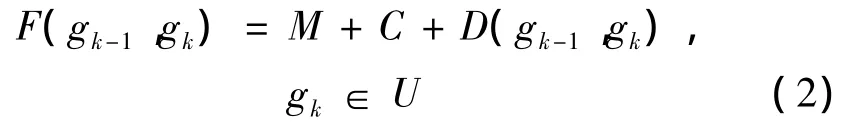
式中gk为禁止通过区时M=∞,否则为0。2个网格之间的距离成本为
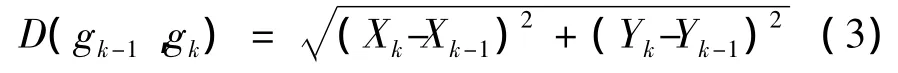
当 gk-1和 gk的连线方向与 gk-2和 gk-1的连线方向相同时有
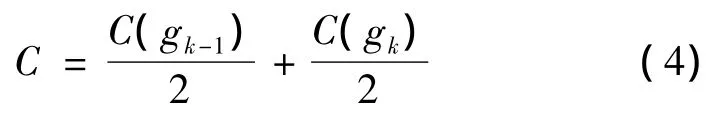
当 gk-1和 gk的连线方向与 gk-2和 gk-1的连线方向不同时有
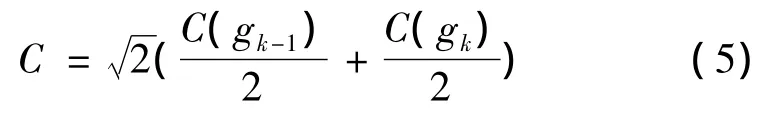
(2)在L2层需考虑距离因素以及交通方便程度,gk-1到gk的可达性成本值为
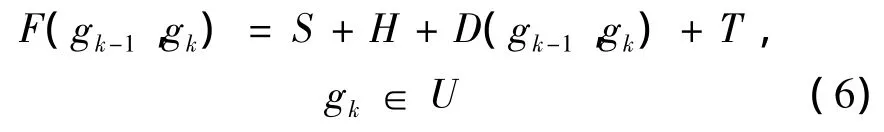
当 gk-1和 gk的连线方向与 gk-2和 gk-1的连线方向相同时有
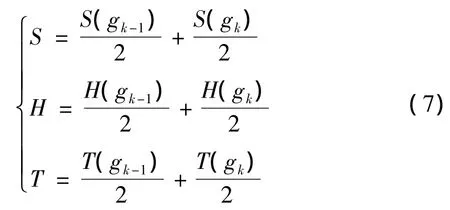
当 gk-1和 gk的连线方向与 gk-2和 gk-1的连线方向不同时有
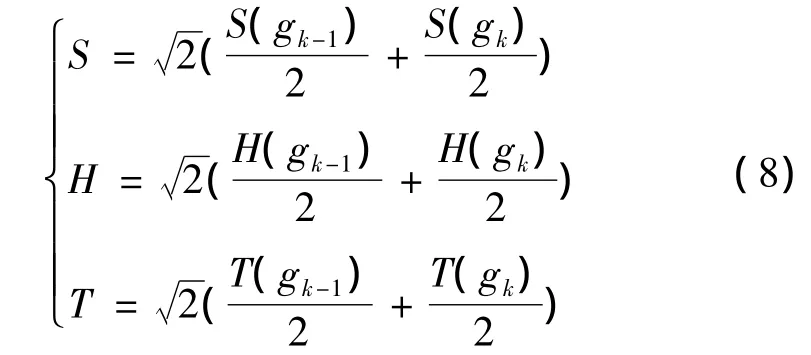
(3)在L3层需要在L2通道的基础上选出一条输电线路,影响因素更复杂。要考虑社会因素中的障碍物、自然因素、经济因素、交通因素。gk-1到gk的可达性成本值为
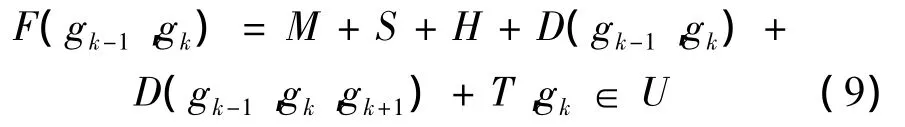
式中:D(gk-1,gk,gk+1)为转角成本值,若没有转角则D(gk-1,gk,gk+1)=0。
算法流程描述如下:
(1)初始化起点、终点和线路必须通过的中间点。
(2)从静态格网数据中读取Lkm×Lkm网格,从动态格网数据中调用协议区、禁止通过区等影响因素,与现有格网叠加分析,生成权重格网。
(3)调用最短路径算法,得出线路可行性通道L1。
(4)读取Mkm×Mkm格网,与L1通道叠置分析,调用动态数据中的道路、河流、矿山、自然保护区边缘等非严格限制因素,再次生成权重格网。
(5)调用最短路径算法,得出线路初选通道L2。
(6)读取Nkm×Nkm格网,与得到的通道叠置分析,调用动态数据中的高速公路铁路、地形(坡度、高程)、居民地、河流湖泊数据,再次生成计算格网。
(7)调用最短路径算法,得出备选线路。其中,Lkm×Lkm、Mkm×Mkm、Nkm×Nkm分别对应着大、中、小尺度的网格单元。
3 实验验证
3.1 实验区说明
本文选取的实验区东西宽约98 km,南北长约34 km,如图2所示。实验区内包含山地、平原、地质公园、森林公园、自然保护区、湖泊、高速公路、铁路、一般公路、密集的村镇、电力线,地形地貌复杂,算法所考虑到的影响因素都包含在实验区内。实验区包含1条中标路径,本文将用该中标路径与本文所用算法提取出的线路做对比,以验证此算法的合理性,然后与Dijksra算法在准确性和精度方面进行对比。
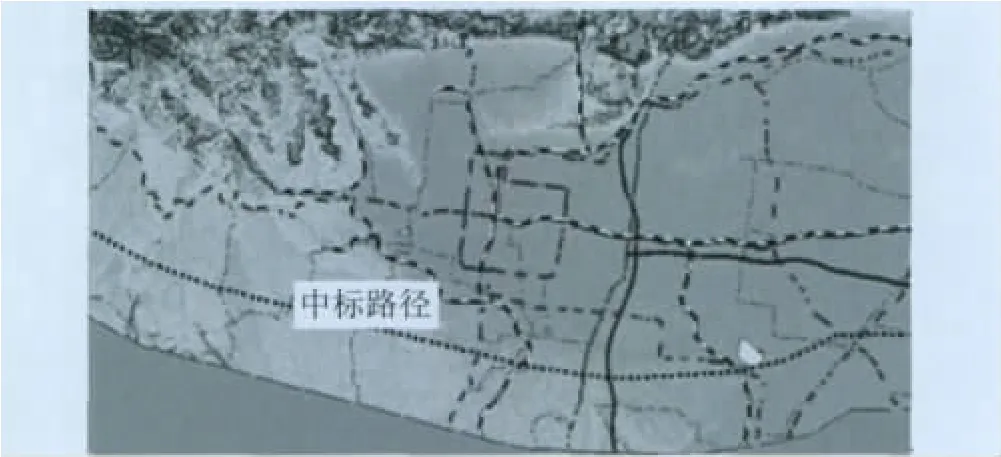
图2 实验区Fig.2 Experimental area
3.2 可行性实验
实验说明:本实验采用网格单元为2 km×2 km、1 km×1 km和0.25 km×0.25 km的分层模型,利用本文提出的算法,在实验区选出1条输电线路,选线结果如图3、4所示。
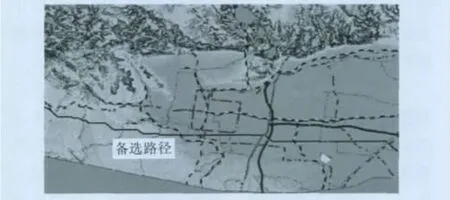
图3 备选路径1Fig.3 No.1 candidate path
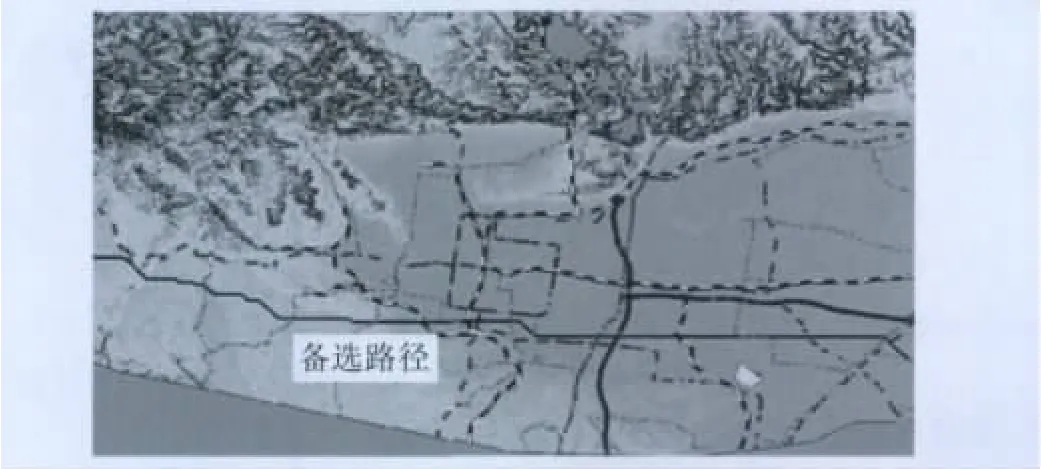
图4 备选路径2Fig.4 No.2 candidate path
由实验结果可知,备选路径1和2的长度均为82.427 km,中标路径长度为80.299 km,备选路径比中标路径多出了2.128 km,这是因为本文提出的算法为了规避陡坡而产生额外距离。3条路径都通过山地和平原,其中坡度大于30°的长度均为0,坡度在10°~30°的路径长度与各路径总长度之比分别为0.164 3、0.16、0.160 9,这说明备选路径与中标路径经过的区域大都是坡度平缓区。备选路径未通过居民地和河流湖泊,而中标路径却通过9个村庄和2个湖泊,这表明本文的方法能准确地避开居民地等障碍物。备选路径和中标路径都与各等级的交通线交叉,都是在交通便利区施工。
通过以上分析可知,利用本文的方法所选出的输电线路,能合理地避开居民地、湖泊以及一些禁止通过区域,并且在地形平坦或坡度较缓的区域通过,和人工选线的结果无异,甚至优于人工选线的结果,比如能够成功地避开居民地,而且选线速度远远高于人工选线。
3.3 速度对比实验
实验说明:本实验先利用Dijkstra算法,在网格单元大小为0.25 km×0.25 km的格网上选出一条输电线路,并记录选线时间T1,然后采用分层模型算法在网格单元为 2km×2km、1km×1km和0.25 km×0.25 km的数据模型上,以相同的起止点选出另一条线路,并记录选线时间T2,以验证在准确性相同的条件下,本文的方法在速度上是否具有优势。
(1)选线结果:Dijkstra算法选线的结果如图5所示,选线耗费时间T1=20 min,分层算法选线的结果如图6所示,选线耗费时间T2=50 s。

图5 Dijkstra算法选线结果Fig.5 Result of route selection by Dijkstra method
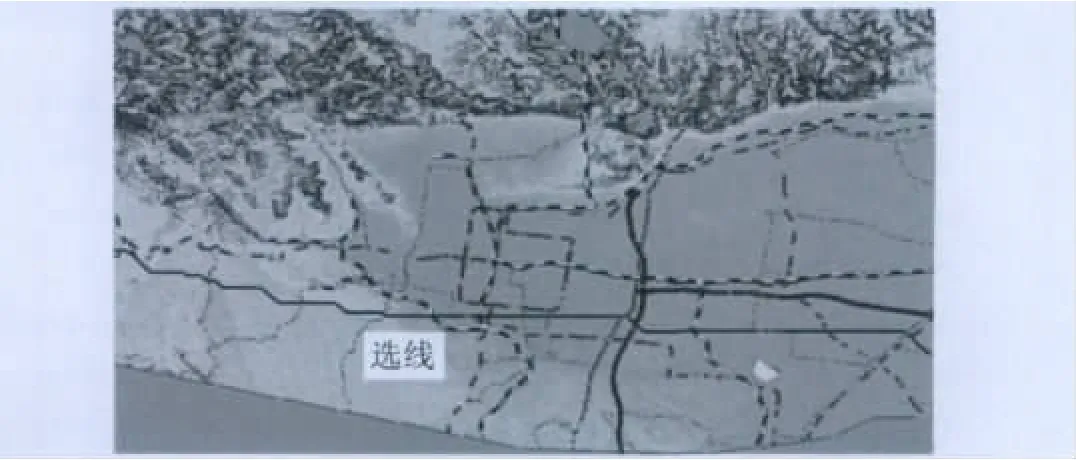
图6 分层算法选线结果Fig.6 Result of route selection by layered method
(2)实验结果分析:由图5、6可知,2种方法选取的线路基本一致。但2种算法选线所花费的时间却差异较大。这主要是由于分层算法采用分层的数据模型,先在2 km×2 km、1 km×1 km的格网上选出1条通道,然后在0.25 km×0.25 km格网上只对该通道所在范围进行运算,这比起直接在0.25 km×0.25 km的网格上运算将大大节约运算量,从而节省时间。
4 结语
本文为解决一般选线算法时间和准确性不能兼顾的问题,提出了基于分层模型的输电线路选线算法,并用实验验证了该算法不仅可行,而且节约时间。列出了该算法需要考虑的影响因子,并将其进行了分类,首次考虑了线路与铁路、高速公路、河流的夹角问题,从而使路径尽量与其夹角大于45°。提出了一种分层次、逐级计算的选线方法,该方法综合考虑了多种影响因子,能快速地选出输电线路,降低了输电线路的选取所花费的时间和成本。
人工选线是凭借选线人员的经验进行,计算机选线则是根据分配的权重来选出合理的线路,而权重则来源于选线人员的经验,因此,如何将选线人员的经验量化为知识库,从而供计算机在选线过程中参考,更准确地确定各个影响因素在不同情况下、不同网格尺度下的权重,将是下一步工作的重点。
[1]Miguel V,Hector G,Sarmiento.Image processing application maps optimal transmission routes[J].IEEE Computer Applications in Power,1996,3(1):33-39.
[2]West N A,Dwolatzky B,Meyer A S.Terrain-based routing of distribution cables[J].IEEE Computer Applications in Power,1997,4(1):42-47.
[3]Cláudio,Monteiro.GIS spatial analysis applied to electric line routing optimization[J].IEEE Trans On Power Delivery,2005,20(2):13-18.
[4]Cláudio,Monteiro.Compromise seeking for power line path selection based on economic and environmental corridors[J].IEEE Trans On Power Systems,2005,20(3):20-25.
[5]Salman A,Hamid E,Valadan Z M.A new method for path finding of power transmission lines in geospatial information system using raster networks and minimum of mean algorithm[J].World Applied Sciences Journal,2008,3(2):269-277.
[6]Volkan Y,Recep N.Developingageospatialmodelforpower transmission line routing[C]//Proceedings of the 3rd Africon Conference.Ezulwini Valley,Swaziland:IEEE,1992:59-64.
[7]Schmidt A J.Implementing a GIS methodology for siting high voltage electric transmission lines[J].Papers in Resource Analysis,2009,11(2):58-63.
[8]Ward J,Fellow I,Ted G,et al.A New method for public involvement in electric transmission-line routing[J].IEEE Trans On Power Delivery,2009,24(4):33-38.
[9]刘春霞,王家海.基于空间分析的送电线路选线方法[J].测绘工程,2008,17(3):28-30.
[10]郑年波.面向动态导航的交通网络数据模型与应用算法研究[D].武汉:武汉大学,2007.
