透视及透视图的研究

艾洪民

（海尔思药业 江西 宜春 336000）

1 透视的基本概念

1.1 透视三维

人们生活在硕大的空间，当需说明某些物体大小和位置关系时，通常都用平面二维加高的（XYH）三维来说明。人们观看空间物体的过程就叫透视，也是投影过程。然而，现在发现另有一个隐形三维可更精准地描述透视投影，即视觉中心（纵轴）再加横、竖两维的三维，可用MNZ表示（见图1）。与一般三维所不同的是，纵轴Z的原点是一端视点S。我们就是在这个透视三维感悟空间和透视物体影像。

图1

1.2 透视图

透视图是反映人们观看空间物体某瞬间印象的画面。基本性质与其他画面一样，都是客观的平面也是若干点、线、面的组合，最基本的还是点。所以绘制透视图也就要逐点、逐线、逐面、逐个地有序描出被视物。透视图用W表示。

1.3 被视物

我们所看到的东西都是被视物。透视图要表现的内容也是被视物，空间被视物投影到透视图上我们同样也要逐点、逐线、逐面、逐个地进行。

1.4 视眼的观看方向

在透视投影中，不能简单地说某人是朝南或朝北方向观看，因为视点有高有矮，视眼观看被视物还有平视、俯视和仰视之分。视眼的视觉中心所指的方向才是视眼的观看方向（见图1中的Z轴）。

2 透视投影

现在我们用透视三维来说明透视投影。首先，把视眼中的影像画面（用mn表示）正立、放大到透视三维的Z轴上，并与MN二维重叠 ，在Z轴具体位置可根据我们所需画面大小任意设定（见图2）。从视点S开始向空间投影点a作连线（或射线），连线（或射线）与mn面的交点就是空间点a在画面的投影。这就是透视投影最精简的图示和描述。

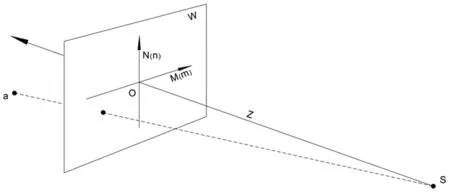
图2

3 透视投影的有效变通

绘制透视图必须要遵循图2所呈现的透视投影规律，但我们不能生硬照搬，因为在平面上我们连标准的三维都画不出来。解决这个矛盾唯一有效的办法，就是用两个二维投影来反映三维投影（见图3）。这样很清楚，我们把投影和成像分开进行。在横竖两个投影面分别获得投影点在画面的横、竖坐标；然后在画面上描出即是投影点的透视图（见图4）。

图3

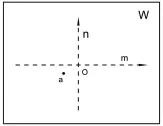
图4

4 实例绘制透视图

4.1 平视被视物

例1：某平面上放有一长方体，它的长宽高分别是120、60和80厘米。视点S高160厘米平视（非仰、府视）长方体，视眼与长方体的位置及视觉方向见图5所示，画出视眼在此处的透视图。

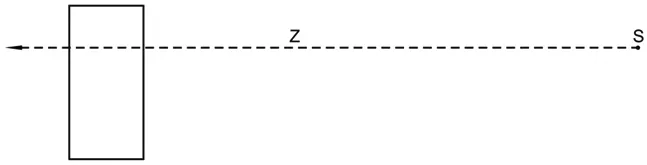
图5

步骤一：投影点的横向投影

在水平投影面通过视觉中心设mZ坐标 （见图6），从S点逐一与方体各投影点作连线或射线，在m轴上找到各投影点画面投影的横坐标。

图6

步骤二：投影点的竖向投影

在平行视觉中心的侧立投影面，通过视觉中心设nZ坐标（见图7），n轴和m轴在Z轴上同一位置，从S点逐一与方体各投影点作连线或射线，在n轴上再找到各投影点画面投影的竖坐标。

图7

步骤三：绘制透视图

在画平面设mn坐标，按各特征点的mn坐标值逐一标出各特征点，再相应连接后擦去mn坐标便是视眼所见长方体的透视图（见图8）。

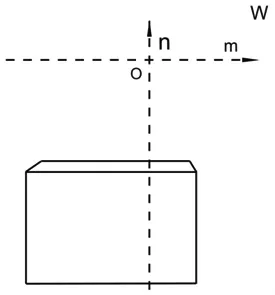
图8

4.2 仰视或俯视被视物

例2：某平面放有一个四棱锥，底边长80厘米，高60厘米。视点高165厘米与四棱锥位置见图9，视觉中心经过锥顶20厘米处，画出相应的透视图。

图9

步骤一：投影点的竖向投影

求投影点画面投影的竖坐标同例1步骤二。同时在此投影面再获各投影点透视三维中的Z轴值（见图10）。

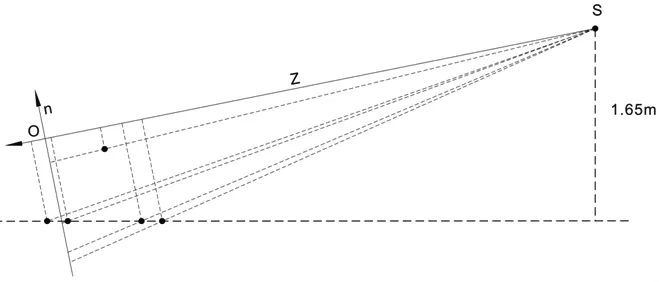
图10

步骤二：找投影点的空间横坐标

在水平投影面里，俯视或仰视时视觉中心轴不反映实长，但通过它加设M轴，可获得各投影点透视三维中的M轴值（见图11）。

图11

步骤三：投影点的横向投影

设M（m）Z坐标，M（m）轴和n轴在Z轴的位置要相同。按投影点的MZ值逐一描出并投影，在m轴上找到投影点画面投影的横坐标（见图12）。

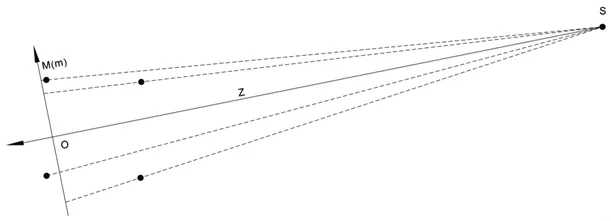
图12

步骤四：描绘透视图

描绘透视图同例1步骤三，四棱锥透视图见图13。

图13

根据这种制图方法的特性，我们可称之为组合投影法。当要描绘多个或形状复杂的被视物时，为防止投影点太多产生混乱，每一投影点的投影、求值、成像几个步骤要同时进行。另外，我们找到投影点的透视三维值后，还可通过计算来获得投影点的画面坐标：

投影点画面横（竖）坐标

本方法过程简单，能真实反映视角范围任何物体的透视成像。整个投影、成像完全数字化，是透视理论的完善也是方法上的创新。它适合人工制图，也必将是下一代电脑制图的基础理论，在不远的将来会更广泛更科学应用于各行各业。

以下仅作参考：

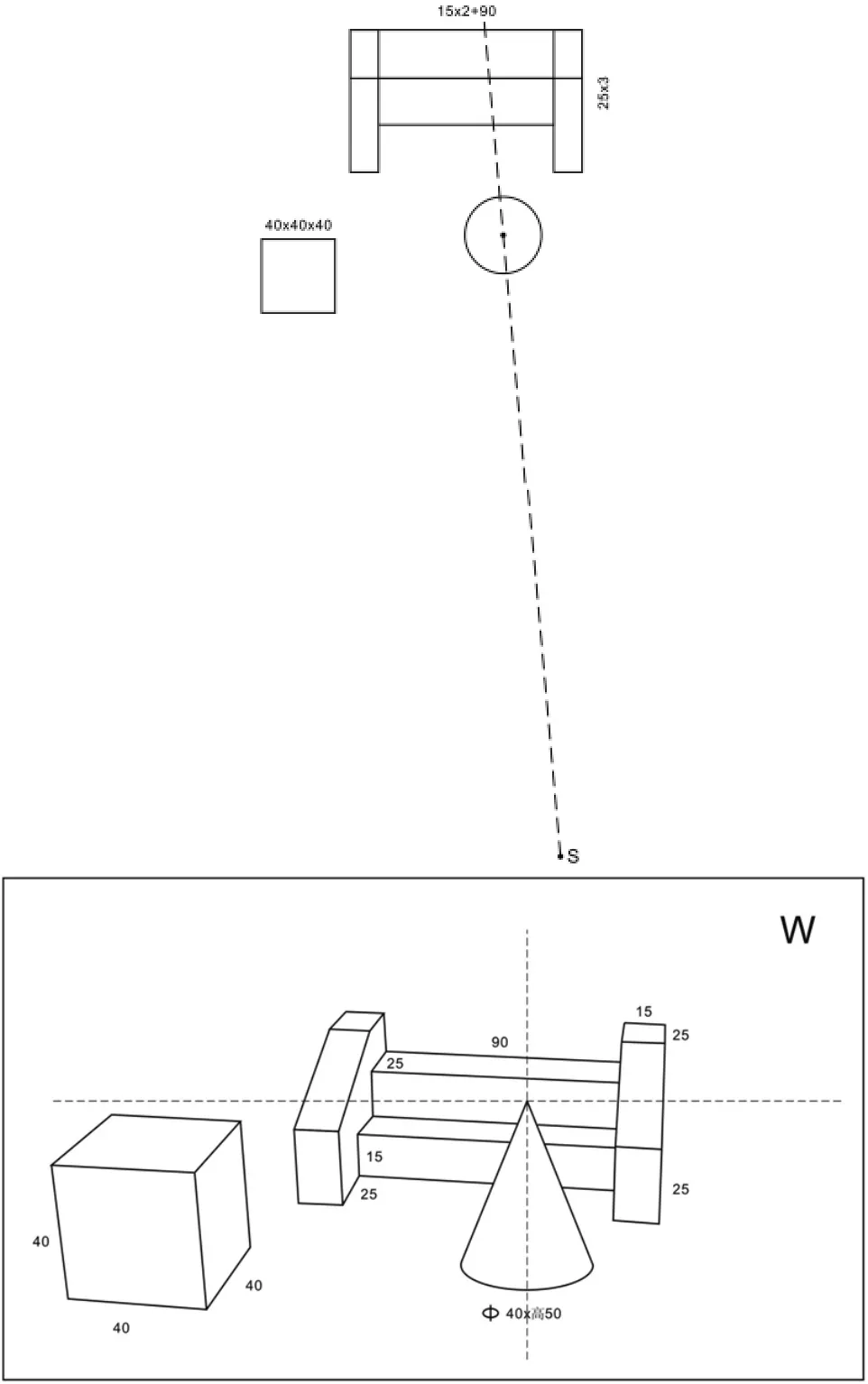
附图 视点高170厘米视觉中心经过圆锥顶点的透视图

［1］艾洪民.二投法绘制透视图：中国,ZL200310110510.6，证书号第283738号[P].2006.