基于小波分析和基因表达式程序设计的短期电价预测

秦江伟，杨 俊，秦 臻

（1.重庆电力高等专科学校，重庆 400053;2.重庆市水利电力建筑勘测设计研究院，重庆 400020）

0 引言

电力市场化是全球电力系统的大趋势，电价又是这个市场的核心，电价的波动影响到各种资源在电力市场中的流动和分配，有着强大的经济杠杆作用，准确的电价预测对于每个市场参与者来说都是极为重要的。特别是短期电价预测已成为电力市场亟待研究和解决的热点课题之一［1］。

本文尝试将GEP运用到短期电价预测中，结合小波分析在处理非线性问题上的优势，建立短期组合预测模型(wavelet-GEP，WGEP)进行短期电价预测。首先利用小波变换对历史电价序列进行分解与重构，得到低频概貌序列和高频细节序列，然后对各子序列分时段建立GEP模型进行预测，最后将各子序列的预测结果相加，从而得到原序列的预测结果。

1 基本原理

1.1 小波变换的基本理论

小波变换是一种窗口大小固定但其形状可以改变，时间窗和频率窗都可以改变的时频局部化分析方法，即具有“变焦距”的特点。在信号低频部分具有较高的频率分辨率和较低的时间分辨率，在信号高频部分具有较高的时间分辨率和较低的频率分辨率。正是这种特性，使小波变换具有对信号的自适应性，特别适合于分析电价这种许多突变和尖峰的信号。

通过小波分解和重构过程，可以很方便地将电价数据进行局部拆分分析和局部拆分后的重构，从而提高电价预测的精度。进行小波变换最重要的是最优小波基和分解尺度的选择。本文采用具有时频紧支撑和高正则性的Daubechies小波对历史电价序列进行分解，经过多次数据实验，最终采用db2小波基对历史电价序列进行1尺度分解，得到的重构信号分别为Ca1、Cd1，其中Ca1为低频的概貌序列，Cd1为高频细节序列。

1.2 基因表达式程序设计

1.2.1 基因表达式程序设计概述

基因表达式程序设计是一种基于基因组和表现型组的新遗传算法，它是遗传算法(Genetic Algorithm，GA)和遗传程序设计(Genetic Programming，GP)相结合的产物，是一种高度有效、稳定的随机搜索方法。

1.2.2 基因表达式程序设计原理与结构

在GEP中有两种东西起主要作用:染色体(基因组)和表达式树(Expression Tree，ET)，后者由编码在前者中的遗传信息的表达式构成。染色体或基因组由一个或多个基因组成的固定长度的线性符号串构成。一个基因由一头一尾两部分构成，头部由包含既代表函数又代表终点的符号构成，而尾部仅仅含有终点。对于每个问题而言，头部的长度h是选定的，而尾部的长度t是h和n的函数，其中n是所需变量数最多的函数的参数个数(也称为最大操作数)，t的大小由下面的方程得到:

1.2.3 基因表达式程序设计算法描述

在GEP中，除了和GA类似的单点重组、双点重组、单点变异等以外，GEP中还包括插串(Insert Sequence，IS)，根插串(Root Insert Sequence，RIS)等具有独特动作和含义的遗传算子。这些遗传算子作用在GEP特殊的遗传编码上形成了具有特色的GEP。图1给出了GEP算法的流程图。

图1 GEP算法流程图

2 WGEP预测模型

本文通过对加州电力市场历史电价曲线的分析，发现电价序列是一个具有多周期的非平稳随机过程，而且价格的突然变化导致序列中出现大量的“毛刺”。鉴于小波变换具有良好的时频局部化性质和变焦性质，而基因表达式程序设计在预测方面的优越性，本文将小波分析和GEP模型相结合，称之为 WGEP方法，并用来进行短期电价预测。WGEP方法的电价预测过程如图2所示。

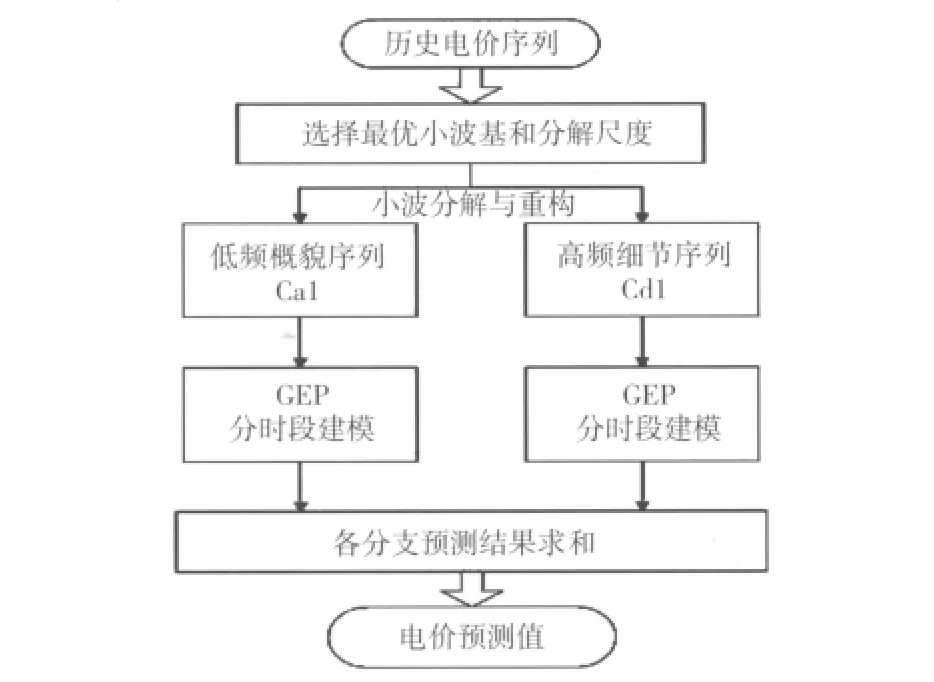
图2 WGEP模型预测流程图

2.1 小波变换算法的改进

目前比较常用的是快速小波变化Mallat算法，在Mallat算法中，输入序列是被假定成无限长，而实际应用中输入序列常常为有限长。此时，分解序列与输入序列卷积时就会出现轮空的现象。在小波变换过程中，当信号为有限长时，会出现边界失真问题，即电价的多层分解在每个子序列的两个边界处都不准确。

图3给出了如下两种方法的误差对比图，法1用小波分析直接对加州电力市场2009年3月1日～3月17日的历史电价序列进行变换，法2用小波分析对加州电力市场2009年2月28日～3月18的历史电价序列进行变换，然后截取3月1日～3月17日的重构电价序列。

如图所示，法1与法2相比，在重构序列的前两个时段和后两个时段出现了较大的失真，鉴于此，本文采用在左边界多取一段历史电价数据进行小波变换保证其连续性，右边界采用周期延拓的方法，进行训练仿真时，将多取的部分去掉。

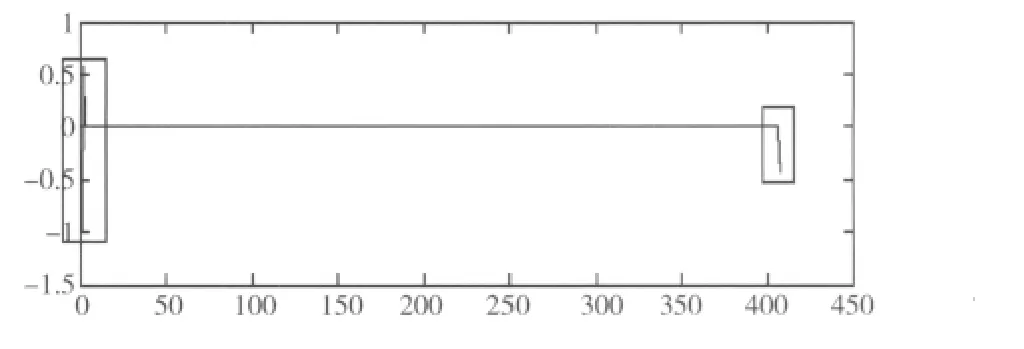
图3 两种方法的误差对比图

2.2 GEP模型的建立

利用小波变换时频局部化的功能，将历史电价序列分解成不同的尺度，得到概貌电价序列Ca1和细节电价序列Cd1，通过对两个电价子序列的分析，概貌电价序列较原序列更为平滑，而且体现出较强的周期性，细节电价序列随机性较强，本文针对不同的电价子序列采用不同的方法建立GEP分时段预测模型。针对去除了大量的“毛刺”且周期性较强的概貌电价序列，本文采用GEP滑动窗口预测模型，而对随机性较强的细节电价序列，则采用GEP预测模型。

滑动窗口预测法的基本思想是:对于有n个数据的时间序列，给定历史长度h，寻找公式f，使得对任意的m(n－h+1≤m≤n)，计算预测值

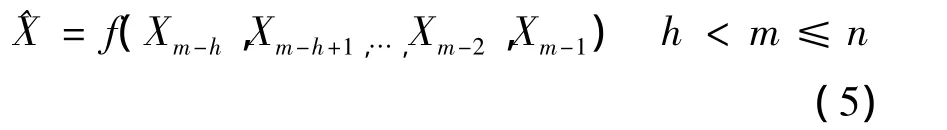
使得预测值与真实值的差别尽量小。整个滑动窗口的预测过程，可以描述为一个长度为m+1的窗口在时间序列数据上滑动，通过窗口中的前h个数据来预测第h+1个数据，其中h的大小就是嵌入维数。考虑到电价序列具有明显的星期周期性，故本文选取嵌入维数为7。

历史电价数据和负荷数据中包含预测时段的细节部分，本文选取预测细节电价序列Cd1(d，t)的输入变量为:提前一天前一时段电价P(d－1，t－1)，提前一天同一时段电价P(d－1，t)，提前一天后一时段电价P(d－1，t+1)，提前两天同一时段电价P(d－2，，t)，提前一周同一时段电价 P(d －7，t)，以及预测时段的负荷L(d，t)，提前一天同一时段负荷L(d－1，t)。

函数集 F={+，–，* ，/，sqrt，exp，log，sin，cos}，其中sqrt表示开方，exp表示e的指定次幂，log表示以10为底的对数。

在GEP模型的训练过程中，采用多基因染色体来进化，即一个染色体(个体)由多个基因连接而成，这里选择“+”作为连接函数。

为找到最优的短期电价预测模型，选择合适的参数非常重要。考虑到电价的相关特性，经过多次测试，选取表1中的参数。

表1 基因表达式程序设计参数设置

本文是在Gepsoft Automatic Problem Solver 3.0平台上建模的，该平台提供了一种新的基因——中性基因。通过一系列的优化运行，我们可以找到当前最好的染色体结构，即直到系统停止改进为止，然后向系统中加入一个中性基因，系统再一次尽其所能地进行搜索，如此这样，直到引入一个中性基因时系统没有改观，最佳适应度不再有任何改进为止。大体上说，这种过程可以让我们在任何精度要求下找到任何连续函数的近似，只要所需要的项足够多。这里，加入的中性基因就是潜在的新的项，而该平台允许这些基因成功地融入这些等式中去。后面的建模过程就是通过5个这样的循环得到的，每次增加一个中性基因。

3 实例验证

采用加州电力市场提供的2009年3月1日到3月17日历史电价数据作为训练数据，对其3月18日的电价进行预测。

因为输入变量中有提前一周同一时刻的电价，依据前述方法，本文采用加州电力市场2009年2月20日到3月17日历史电价数据，其中17日的电价数据再向右进行周期延拓(共648个电价数据点)，作为小波分析的历史电价序列。对历史电价序列进行小波多分辨率分析，分解水平为1，对其系数进行重构，得到分解后的概貌电价序列与细节电价序列。

图4 用小波变换对历史电价进行多分辨率分析

图4所示为去掉多取部分(左右24个数据)后的概貌序列和细节序列，通过与对加州电力市场2009年2月20日到3月18日历史电价数据进行小波变换后，截取2月21日到3月17日的概貌序列和细节序列完全吻合。

用GEP模型分别对概貌序列和细节序列进行分时段预测。经过演化计算得到24h整点时刻的48个预测模型，限于篇幅，仅列出了1时段的2个预测模型，分别为

1时段:

其中:d0－d7分别为前7天、前6天、…、前一天的概貌电价。g2c5=0.631195，g2c8=0.237182，g2c9=－0.086303，分别代表第二个基因的随机常数组 A={0.021789，－0.871766，－0.451202，－0.115783，－ 0.79538，0.631195，0.911713，0.908112，0.237182，－0.086303}中的第5、8、9 号随机常数，数组A以0号随机常数开始。同理，g3c6=0.189361。

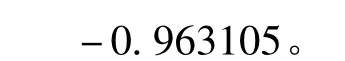
概貌序列和细节序列的预测结果如图5所示，从图中可以看出，GEP对概貌序列和细节序列的拟合程度都比较好，各时段的复相关系数都达到了90%以上。

为了对比，本文分别用了四种模型进行电价预测，模型1、模型2分别为文献［7］所采用的ARIMA模型和WARIMA模型，模型3直接采用GEP进行预测，模型4为WGEP模型，其实际值、绝对误差、相对误差如图6所示。

从实际电价和四种模型的预测结果可以看出，GEP模型的预测精度明显好于ARIMA模型，最大相对误差和平均相对误差都明显减小，其中最大相对误差 ARIMA模型为 11.83%，GEP模型为9.48%;平均相对误差ARIMA模型为5.17%，GEP模型为4.22%，结果表明，将GEP方法用到短期电价预测中是有效的、可行的。

此外，WARIMA、WGEP这两种组合模型的预测精度也明显要高于单一模型的预测精度，表明小波分析在电价预测中的作用是显著的。文献［7］对加州电力市场2009年3月1日到3月17日的历史电价数据进行小波分析，将失真的数据引入到模型中，造成了前两个时段和后两个时段的预测误差较大，本文对小波变换的边界问题进行了处理，从仿真的结果可以看出，这几个时段的预测精度得到了明显的提高，其中1时段的预测误差较WARIMA模型偏大，是由于GEP对概貌电价的拟合程度不够所造成的。WGEP模型相对于WARIMA模型预测精度也有所提高，其中最大相对误差 WARIMA模型为9.48%，WGEP模型为6.72%;平均相对误差WARIMA模型为3.03%，WGEP模型为2.70%，此外还分别对加州电力市场2010年1月26日和2月27日的24个时段电价进行了预测校验，所得相对误差分别为3.56%和2.98%，较 WARIMA模型的3.77%和3.11%有所降低，表明WGEP模型用于短期电价预测效果令人满意，且方法简单可行。

4 结论

(1)小波变换是对时域内暂态信号进行分析的有力工具，可以实现对信号由粗到精的分析。小波变换能将各种交织在一起的不同频段组成的混合电价信号分解成不同频带上的块信号，即将电价序列分别投影到不同的尺度上，各个尺度上的子序列揭示了电价序列在不同层次上的详细结构，反映了电价的各种信息。

(2)基因表达式程序设计是一种高度有效、稳定的随机搜索方法，无需事先确定预测模型，能从大量看似无规则的数据集中挖掘出未知的、有价值的函数模型用于预测，将其运用到短期电价预测中比时间序列法具有更好的预测精度。

(3)基于小波分析的GEP模型对于短期电价预测具有较好的预测精度，通过小波变换后的信号比原始信号平稳性要好得多，更有利与预测建模，加上GEP对各电价子序列有较好的拟合精度，实例验证，WGEP方法在短期电价预测中具有较好的预测能力。

(4)本文较好地处理了小波变换的边界问题，避免了将失真的信号引入到训练样本中，从而造成较大的误差。仿真结果表明，在两个边界时段，预测精度得到了提高。

［1］ 张显，王锡凡.短期电价预测综述［J］.电力系统自动化，2006，(3):92-101

［2］ Wang A，Ramsay B.Prediction of system marginal price in the UK power pool using neural networks［C］.Proceedings of International Conference on Neural Networks，Houston(TX.USA)，1997:2116-2120.

［3］ HONG Y，HSIAO C.Locational Marginal Price Forecasting in Deregulated Electric Markets Using a Recurrent Neural Network.In:Proceedings of IEEE PES Winter Meeting，Vol 2.Columbus(OH，USA)，2001:539-544.

［4］ CONTRERSA J，ESPINOLA R，NOGALES F J et al.ARIMA Models to Predict Next-day Electricity Price.IEEE Trans on Power Systems，2003，(3):1014-1020.

［5］ ZHOU Ming，YAN Zheng，Ni Yi-xin et al.An ARIMA Approach to Forecast Electricity Price with Accuracy Improvement by Predicted Errors.In:Proceeding of IEEE PES General Meeting. Denver(CO，USA)，2004:233-238.

［6］ 霍利民，范新桥，黄丽华，等.基于基因表达式程序设计及误差循环补偿的电力系统短期负荷预测［J］.中国电机工程学报，2008，(28):103-107.

［7］ 周明，聂艳丽，李庚银，等.基于小波分析的短期电价ARIMA预测方法［J］.电网技术，2005，(9):50-55.