基于建筑物沉降数据的小波去噪与预测分析

2012-02-08吴欢陈刚

城市勘测 2012年3期

吴欢，陈刚

(1.江西理工大学建筑与测绘工程学院，江西赣州 341000;2.郑州测绘学校，河南郑州 450015)

1 前言

为了保证建筑物的安全，在实际生活中需要用测量仪器对建筑物进行沉降监测。由于建筑物产生沉降受各种不确定因素的影响，所以通过观测所得来的沉降数据中包含了很多噪声，噪声的存在对信号的本质特征会产生严重的影响，如果直接在此数据的基础上进行沉降预测，得到的预测结果在精度上往往达不到要求，这就给沉降预测工作带来了不便。

由于变形体的不同状态间具有时间关联性，因而变形监测的数据是关于时间变化的动态数据序列［1］。小波变换［2］适于分析由长时低频成分和短时高频成分组成且无太多先验知识的信号。将小波分析方法用于建筑物变形监测数据(信号)的处理之中，消除观测误差(噪声)，即可得到去噪之后的观测数据，然后对去噪之后的数据进行预测分析。

2 基本原理

利用小波分析去噪，即在不同尺度下作小波变换，把那些主要反映噪声频率的尺度小的小波变换去掉，即可得到质量较好的有用信号。将观测信号中的真实信号与噪声信号尽可能进行分离，即对有效的信号进行保留，对噪声信号进行排除，即为小波变换去噪的实质。小波变换的基本思想是对于某一信号或者函数利用小波函数去进行逼近。利用小波变换多分辨率的特点可以有效地对信噪进行分离，最后再把去噪后的小波系数进行信号的重构，得到真实信号的最优估计［3］。根据得到去噪后的信号，然进行灰色建模预测。

3 实例分析

本文以某城市主体建筑进行沉降观测数据为例，该建筑主体基础形式为筏板，结构地上25层，地下2层。本项沉降监测采用NA2水准仪，配合使用因瓦尺，按测微水准测量方法施测。本文选取了其中S1、S2两个监测点作为研究对象，采用本文提出的方法对这两个监测点进行沉降数据处理，并选择监测点S1的数据进行预测分析。监测点的已知数据均为2005年7月(施工开始)到2006年9月(施工即将结束)之间的监测点沉降监测数据。本文使用的是观测后累计沉降量，具体数据如表1所示，显然，这些数据可以视为离散信号序列，从而可作为原始信号。

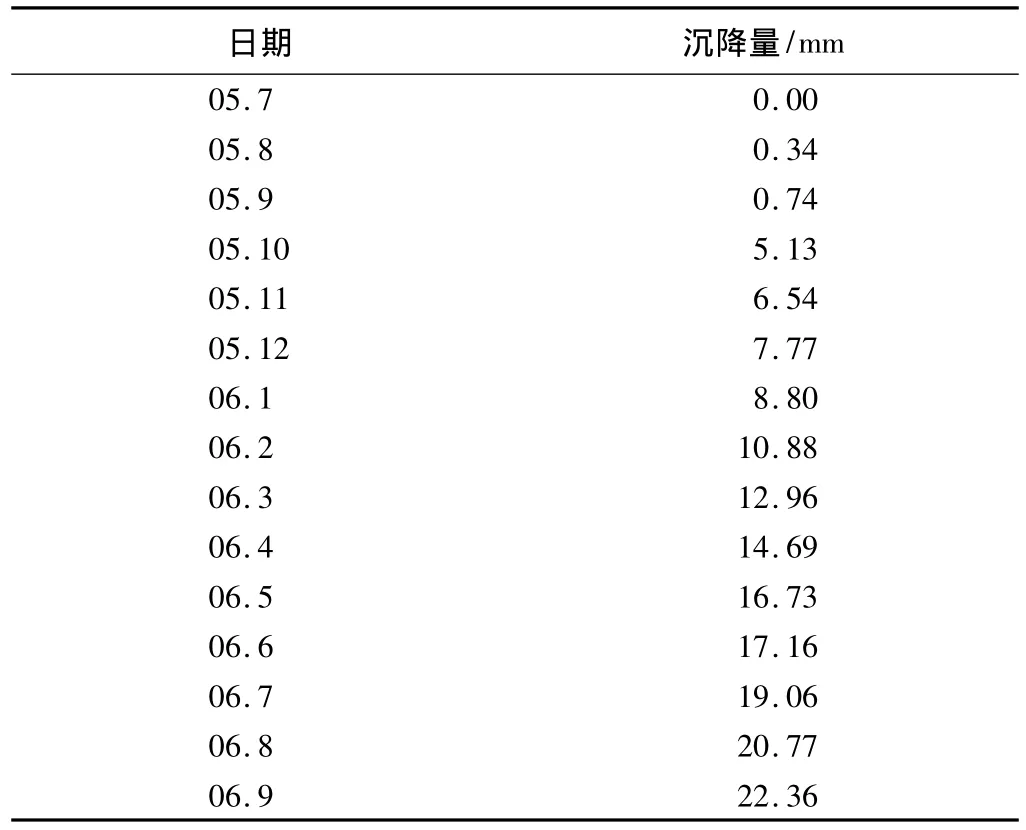
S1号监测点沉降监测数据表1

选取S1监测点的沉降数据，利用MATLAB得到其沉降量趋势曲线图，如图1所示。

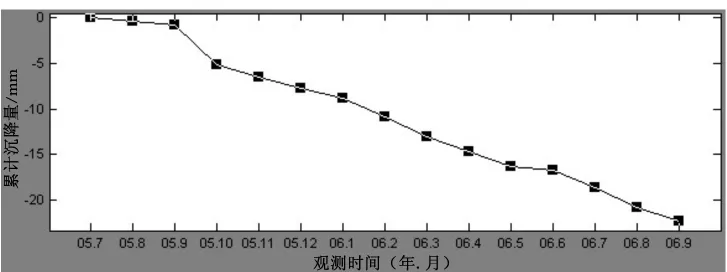
图1 S1监测点的沉降量趋势曲线图

从图1中可以看出S1监测点细节变化不是很平稳。在实际观测过程中，由于各种原因产生的随机误差的影响，使得观测数据里带有噪声，应该尽可能在该信号中提取出实际变形值，在安全监测中，监测数据反映的是被监测对象的变化趋势，它是典型的时变信号，如果直接用此原始数据进行建模预测，就会使预测精度降低，因此我们需要对原始数据进行去噪处理。

根据小波去噪理论［4］的分析，结合本文实验的需要，基于小波工具箱GUI实现方式，在消噪过程中，采用Db4小波对原始信号进行三层分析。为了获得好的去噪效果，合理选择阈值非常关键，常用的有4种阈值可供选择，本文选择heursure启发式阈值［5］。图2、图3所示为滤除高频噪声后S1、S2监测点累积沉降量的去噪效果。

图2 S1监测点累积沉降量的去噪效果

图3 S2监测点累积沉降量的去噪效果

从图2、图3中可以看出，在利用Db4小波去噪后信号已经不会有很大的抖动且逐步趋于平滑，达到去噪的目的，有效地去除了观测中的高频噪声，真实数据得到了释放，得到了预测所需要的数据。去噪后的具体数据如表2所示。

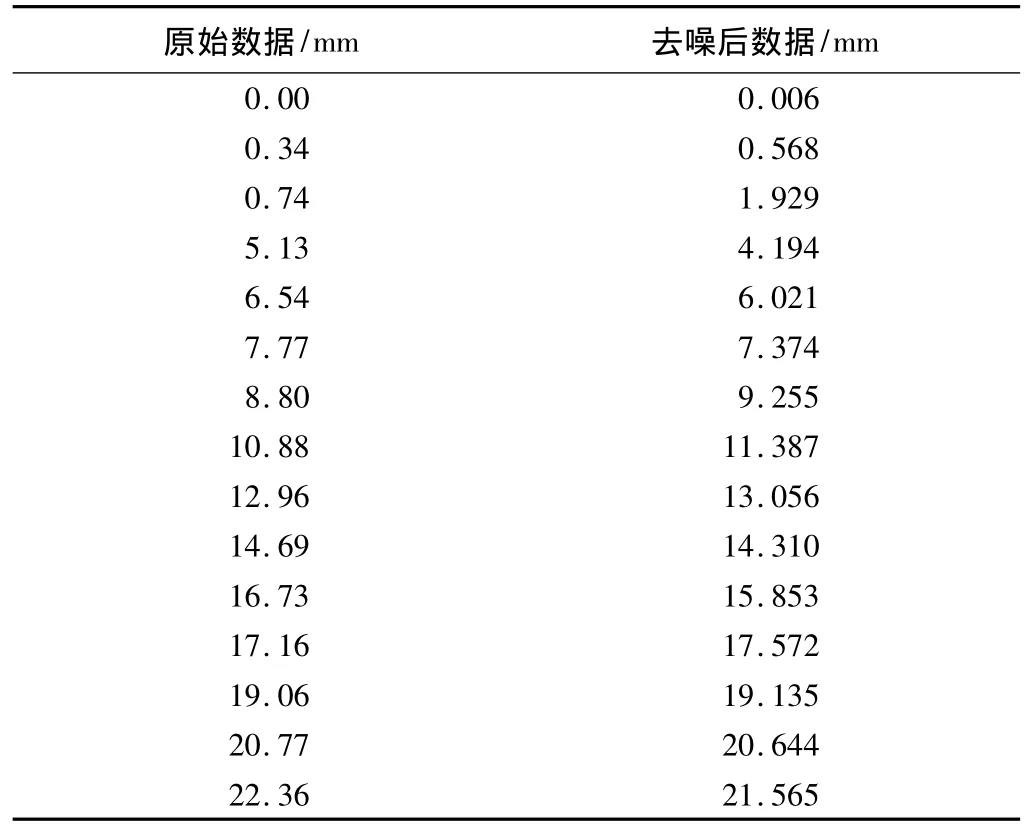
S1监测点原始数据和去噪后的数据表2

4 沉降变形预测

根据去噪后的数据，在灰色理论［6］的基础上，结合实际监测数据建立了灰色GM(1，1)预测模型。灰色理论是一种动态模型，即它是利用离散随机数经过生成变为随机性被显著削弱而且具有规律的生成数，建起的微分方程形式的模型，这样便于对其变化过程进行研究和描述，我们记其为 GM(Grey Model)［7］。

4.1 灰色建模步骤

GM(1，1)模型预测主要是对原始数据序列利用AGO生成进行趋势化，然后建立分方程，具体步骤如下［8］:

GM(1，1)模型需要进行精度检验，本文采用的是后验差检验方法，模型精度由均方差比值和小误差概率共同评定。后验差方法一般是按后验差比值C和小误差概率P两个指标综合评定预测模型的精度。具体步骤如下:

设 X(0)为原始序列(实际值)，^X(0)为 GM(1，1)模型模拟序列(预测值)，则残差:

精度检验要求后验差比值C尽可能小，指标P尽可能大。一个优秀的模型要求C＜0.35，最大不超过0.65;P＞0.95，不得小于 0.70。

4.2 灰色预测模型建立与分析

本文选取了S1监测点的2006年1月～7月沉降数据经过小波变换去噪后的数据为样本数据，对2006年8月～9月的数据做出预测。

预测数据为:X(1)的紧邻均值生成序列为:

通过该模型对经过小波变换去噪后的数据进行灰色建模预测，得到2006年8月和9月的预测值，将其和单纯的灰色预测结果进行比较，具体的计算结果如表3所示。

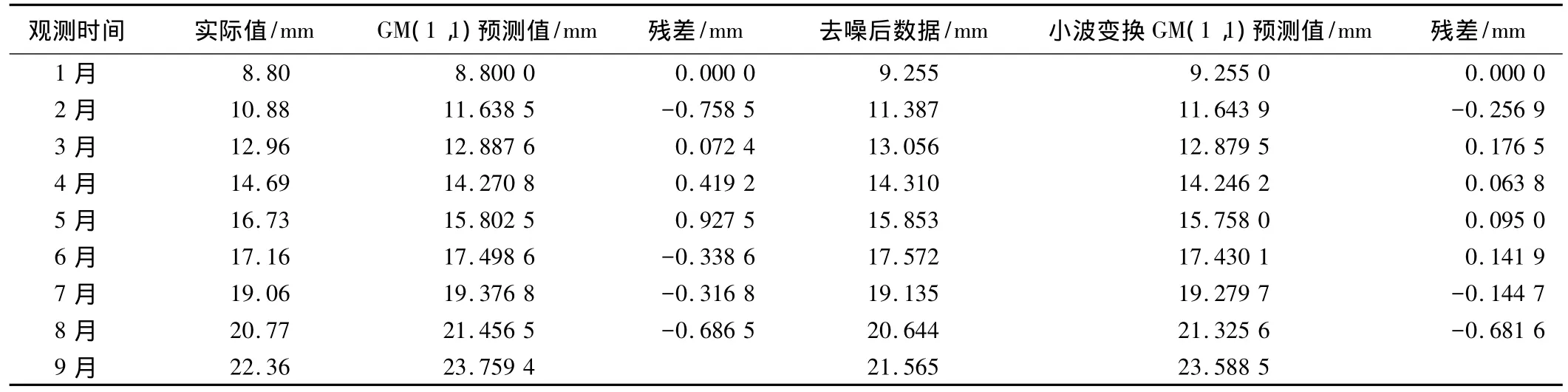
S1监测点灰色预测模型的相关数据对比表3

从表3中可以看出，8月份的灰色预测值为21.456 5 mm，小波变换灰色预测值为 21.325 6 mm，而去噪后的值为 20.644 mm，9月份的灰色预测值为23.759 4 mm，小波变换灰色预测值为 23.588 5 mm，而去噪后的值为 21.565 mm。通过编制的MATLAB程序，得出该GM(1，1)预测模型小误差概率P=1，预测精度为一级。对原始监测数据序列直接用灰色模型预测的后验差比值为 0.022 7，而经过小波变换去噪后再进行灰色模型预测的后验差比值为 0.002 1。精度检验要求均方差比值越小越好，比值小表明原始数据虽然很离散，但预测使用的样本数据与通过模型得出的计算值之差并不太离散。

由此可见，经过小波变换去噪后再进行灰色建模预测能够提高预测精度且小波变换灰色预测结果优于单纯的灰色模型预测结果。