基于混合优化算法的RLV 覆盖区求解
2012-02-07李惠峰孙国庆何睿智
李惠峰 孙国庆 何睿智
(北京航空航天大学宇航学院,北京 100191)
1 引言
近年来由于可重复使用运载器(Reusable Launch Vehicle,RLV)拥有大的纵程和横程机动能力,受到各国科研人员广泛的关注,各个国家均已投入大量人力、物力进行研究。当飞行器再入时,飞行器需要较长一段时间在大气层中飞行,将受到热流密度、动压、过载的严格约束,又由于飞行器需要进行主动姿态控制,给飞行器材料和内部设施热绝缘带来巨大的挑战,所以飞行器安全、可靠的再入成为非常重要的问题。
再入飞行器覆盖区是指飞行器以某一初始条件再入在地球表面能够获得着陆的范围,是评估再入飞行器航程覆盖能力的重要性能指标。当再入飞行器返回时,通过覆盖区的信息和飞行器的状态来确定飞行器的着陆点。
国内外的研究工作中主要有四种覆盖区求解方法:通过坐标旋转将覆盖区求解转化为在自由纵程下最大横程的参数搜索问题[1];利用直接法转换为轨迹优化问题[2-3];通过最大和最小阻力包线近似判定覆盖区外边界和内边界[4];文献[5-6]中论述在规定的纵程下,最近轨迹和最大横程问题,两个问题解决方法相同,将覆盖区问题转化为最近轨迹下的单一参数搜索问题。大部分方法在求解覆盖区问题时都需要进行参数搜索,而且往往是多参数搜索,传统的参数优化主要有基于极大值原理的间接法和基于非线性规划理论的直接法[7]。但无论是直接法还是间接法,都需要根据工程经验设置参数初值,然后通过试错法对这些参数进行调整,而目标函数对待优化参数的微小变化十分敏感,给全局寻优带来很大困难,很难找到全局最优解,并要花费大量的时间。所以优化结果的好坏在很大程度上取决于某些优化变量的初始猜测值以及优化算法的性能。
本文针对覆盖区求解过程中优化参数的初值选取和优化算法性能与效率问题,利用多学科优化软件,找到参数优化的初值点,基于参数的响应面特性,在分析全局优化算法和局部优化算法优缺点的基础上,设计了混合优化算法,将具有较好全局优化性能的遗传算法和局部优化性能突出的模式搜索法相结合,仿真结果表明混合优化算法具有精度高、收敛快等特点,能够准确且高效地获得再入覆盖区,有很好的工程实用价值。

图1 覆盖区示意Fig.1 Illustration of footprint
2 覆盖区问题建模
(1)覆盖区问题描述
本文在求解覆盖区时,采用定纵程下的最大横程方法来求解。如图1所示,E为再入点,ED 是最大的纵程,AD 和CD 是给定的纵程(EB1,EB2,…,EBK)下最大横程的集合,AC 是最小纵程的集合,覆盖区定义为被AD、CD 和AC 连接包围的范围。这里不考虑最小纵程的集合AC,主要考虑外边界AD 和CD 的求解。
(2)无动力再入运动方程
考虑地球为旋转圆球旋转时,引起的科里奥利力(Coriolis Force)和牵引力引起的影响,RLV 无动力再入飞行器,在极坐标系下的量纲一运动方程为

为了提高数值计算精度,对各变量进行归一化处理,即用原变量除以对应的归一化系数,其中r为地心矢径长度,归一化系数为地球半径R0;V 是速度,归一化系数为L,D 是气动升力和阻力,归一化系数为mgn,相应的升力系数为CL,阻力系数为CD,m 是飞行器质量;γ是航迹倾角;σ是滚转角;θ,φ是经度和纬度;ψ 是方位角;Ω 是地球自转角速度。时间t采用进行归一化,控制变量为滚转角σ和攻角α。如无特别说明,下文中变量均为归一化变量。
采用以下假设条件:重力加速度为常值gn;满足准平衡滑翔条件;高度为常值且r=1;不考虑地球自转,忽略哥氏加速度与牵连加速度。经简化处理得到三自由度运动方程:

(3)平衡滑翔约束条件
对于再入飞行器而言,再入过程受到动力学和物理学约束,比如气动加热,过载及动压约束[6],再入飞行器以高超声速在大气层中飞行时,空气受到强烈的压缩和摩擦作用,大部分能量转化成热能,导致周围空气温度急剧升高,而且热能迅速向飞行器表面传递,引起严重的气动加热问题。如果气动加热过度,会损坏飞行器和内部设备,所以对温度的限制十分有必要;而机体结构和运载器表面放热材料的强度决定了飞行器的动压约束;飞行器在飞行时受到载荷作用,当载荷超过承受极限,飞行器结构和内部仪表可能会遭到破坏,因此也需要对飞行器所受的总过载进行限制。这些常规约束对再入过程影响很大,此外为保证平滑再入飞行,还要考虑准平衡滑翔约束。
对具有高升阻比的再入飞行器,在进行滑翔飞行时,其法向加速度较小,从而导致航迹倾角以及航迹倾角变化率很小。由此,高声速飞行器三自由度再入运动方程组中,表示航迹倾角变化的微分方程,就可以通过将航迹倾角变化率近似为零进行简化,这个代数式就是平衡滑翔条件。平衡滑翔条件给出了飞行器滑翔轨迹上速度与高度很重要的关系式,通过将其应用到升力体飞行器再入相关问题的研究中,能够显著降低问题的维数与难度。但是,在对平衡滑翔的实际应用中发现,飞行器的航迹倾角变化率不会理想地保持为零,它随时间在很小的范围内缓慢变化,很多情况下航迹倾角出现小幅值的长周期震荡动态。在这种情况下,平衡滑翔条件在实际应用中改称为准平衡滑翔条件(Quasi-Equilibrium Glide Condition,QEGC):

利用QEGC中给出的速度-高度关系可以将飞行器再入中的过程约束转化为对滚转角控制量σ最大值的约束,热流率约束、动压约束以及过载约束对应的滚转角最大值分别用σmax_Q(V)、σmax_q(V)和σmax_n(V)表示,具体值计算:
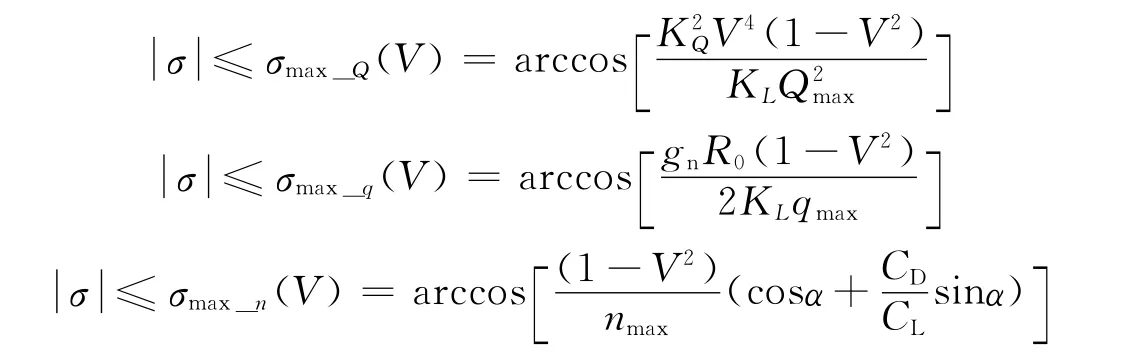
式中 Qmax、qmax和nmax为飞行器所允许的最大热流率值、最大动压值以及最大过载值;KQ为与飞行器自身有关的常数;KL=R0SrefCL/2m,Sref为飞行器参考面积,m为飞行器质量。综上所述,滚转角的最大取值为
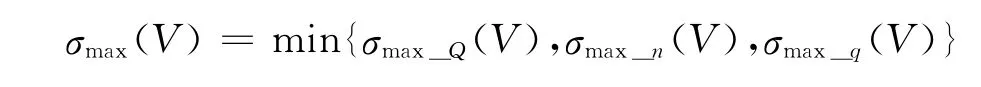
3 最优控制问题
(1)给定纵程下的最大横程问题
对定纵程下最大横程问题,通过轨迹最优控制,使得飞行器从再入点E(由经纬度θE和φE表示),在给定纵程SP(对应点P,由经纬度θP和φP表示)下,达到最大横程SF(对应点F,由经纬度θF和φF表示)。优化目标是使得横程SF最大,性能泛函

终点约束条件主要有两个:达到预设的末端能量;EP 与PF 的夹角为直角:

式中 rf和Vf是终端高度和速度。
哈密顿函数可写为

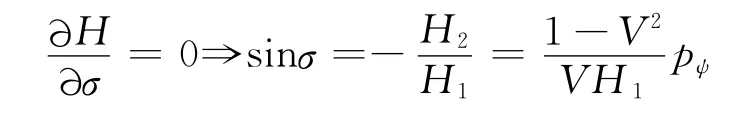
由于时间t并不显含于哈密顿函数中,所以有:

式中 P为伴随变量矢量;x为状态变量矢量;c0为常数。则可得:

同时由H2和H3的表达式可以得到:

经过一系列推导(具体过程参见文献 [8]),最终可得到滚转角最优控制律为
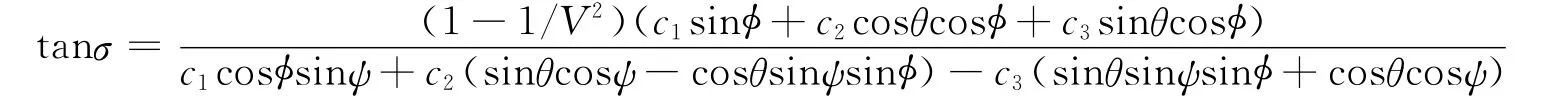
在滚转角表达式中,分子分母都是积分常数c1,c2以及c3的线性表达式,由此可见,滚转角表达式的值只与其中两个独立变量有关,最终的优化目标也就是要找到这两个独立变量的具体值。结合最大滚转角约束条件可得:

式中 σ*为设计的滚转角控制律,且|σ|<π/2。由于末端航迹偏角不固定,可以是任意值,由最优化理论易知:

参数c1,c2和c3中只有两个独立变量,假设:c2=sink,c3=cosk,上式整理可得:

至此定纵程下最大横程优化问题表述为:在满足终点约束条件的前提下,利用一系列的寻优算法求解最优控制参数c1和k的值。
(2)最大纵程问题
对于最大纵程问题,性能泛函为

终点约束条件为末端能量约束,如式(1)所示,对于第2节中的再入动力学方程,从初始再入点开始,采用零度滚转角控制律对轨迹进行积分,当再入轨迹的能量变量满足终端能量停机条件时,轨迹积分停止,得到的轨迹终点即为最大纵程点D,计算得到该轨迹对应的纵程即为最大纵程ED。
4 参数优化分析
在第3节的问题求解中把能量条件设置为停机条件,当飞行器能量因子达到预设值,那一时刻的飞行器所处点就作为再入轨迹飞行的终端点,需要求解两个参数(c1,k)以使其满足非线性终端约束方程:

对于该双参数寻优问题,基于这两个非线性函数,构造一个性能泛函J(c1,k):

令ω1=ω2=1,得到性能泛函J(c1,k)在区间c1∈[-1.5,1.5],k∈[-π,π]的扫描图(图2)。这是一个很不规则的参数响应面,具有很多局部凹槽,并且对参数的微小变化十分敏感。可以看出将非线性函数J1(c1,k)与J2(c1,k)取平方和会造成新的性能泛函J(c1,k)出现很多凹凸面,使得在基于梯度方法进行搜索时很容易陷入局部最优的情况,很难找到全局最优解。
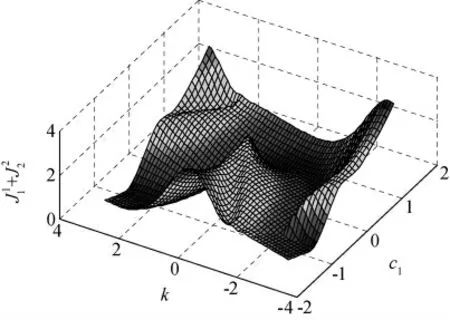
图2 性能泛函J 扫描Fig.2 Performance index J
通过对整个可行域内的参数响应分析,可以发现对于该具体的飞行器寻优问题,在整个可行域内有4个最优点,通过编程求解方程必定可以得到初始的一个解,对于其他的解,则可以通过一定的波动或者改变搜索范围进行查找。但由于滚转角控制律中,分子分母均为参数的线性表达式,所以导致了这4个最优解实际的物理意义有所不同,实际上只有两个解是最优解,一个是左边最优点,一个是右边最优点。另外两个“最优点”虽然对于该飞行器再入阶段的滚转角控制量是一样的,但在二阶特性中,是不满足条件的,应该舍弃。
优化算法可以分为两大类:全局优化算法、局部优化算法。相比较而言,全局优化算法收敛速度较慢,而局部优化算法收敛速度快。但局部优化算法存在一个初始点的选取问题,如果初始点选取不够准确,将有可能使搜索进入局部极值,结果不准确。
基于多学科优化软件OPTIMUS所集成的优化算法对典型的优化算法进行测试。全局优化算法包括:差分进化、自适应进化、模拟退火。局部优化算法包括:序列二次规划、非线性二次规划、广义简约梯度。六种优化算法所对应的优化结果精度分别为:0.000 26,0.000 22,0.000 38,2.556 13×10-5,0.000 56,3.391 79×10-5。通过对比分析优化结果,得出如下结论:1)全局优化算法不需要给定初始点,在整个参数可行域内进行概率搜索,得到的优化结果往往较接近于全局最优点,但精度不高;2)如果给出的初始点位置较好,局部算法要明显短于全局优化算法,而且局部算法可以设置非常短的迭代步长,精度较高;3)局部算法出错的可能性较高,这是由局部算法本身的特性所导致的,局部搜索算法依赖于给定的初始点,敏感性非常强,如果给定的初始点离全局最优点较远的话,往往容易陷入局部极值点,得到错误的结果。
从平台全局算法的优化结果,可以看出当得到最优结果的同时,也得到了全局最优点,可以将其作为初值点写入局部优化算法中,以缩短局部寻优时间。
5 混合优化方法
根据第4节分析,提出一种结合不同方式的优缺点的混合优化方法,将全局优化得到的优化结果点作为局部优化的初始点进行进一步精确搜索,得到更加精确解,满足全局最优性,而且可以极大地降低错误率。
5.1 遗传算法
遗传算法的特点在于其直接对结构对象进行操作,不需要导数信息或者要求函数连续,具有很好的全局搜索能力,不需要给出初始点,采用概率化的寻优方式能自适应地调整搜索方向。其算法分为以下步骤:
1)第一步:编码。将可行域中的优化设计向量进行编码。在规定的搜索区间内(c1可行域[-1,1],k可行域 [-π,π]),对两个变量进行编码,编码形式为码长100的二进制码,前50个表示参数c1,后50个表示参数k。
2)第二步:形成初始群体。随机选择若干个体形成初始群体,初始种群个数设置为1 000个。
3)第三步:计算适应值。与目标函数直接相关,有相同的极值点。
4)第四步:选择。将适应值累加,利用赌轮盘法进行选择。
5)第五步:交叉。选择交叉概率为0.6,从交配池中随机取出几个个体配对,确定交叉点,将选中的个体在交叉点以后的编码数字进行交换。
6)第六步:变异。选定变异概率为0.01,对应编码的每一位也用随机小数表示,小于变异概率就求补运算,进行变异。
对于初始种群中的所有样本点,计算其适应值,利用赌轮盘的方法进行选择交叉,同时以之前设定好的变异概率对种群中的“基因”进行变异。不断迭代循环,每一步记录下该步迭代的最优点,直至最终的遗传代数达到设定值20。搜索结束,记录下迭代最后的“最优点”。
5.2 模式搜索法
模式搜索法是一种从几何意义上提出的参数直接寻优局部搜索算法。该算法不需要对目标函数求导,可以解决不可导函数以及求导复杂函数的参数寻优。基本方法为:从初始点开始,依次向四周进行搜索,一旦发现比当前点的函数值更优的点,就将该点作为下一个搜索周期的起始点进行下一步迭代,直至最后的点的四周均没有比当前点更优的点时,寻优结束。模式搜索法受初始搜索点的选取影响很大,具有较快的收敛速度,但并不具有全局最优特性,容易进入局部最优“凹槽”,搜索步长也需要根据具体问题进行选取。具体步骤为:
1)确定初始搜索点。将遗传算法得到的“最优点”作为模式搜索法局部搜索的初始点。
2)求周围点函数值。以初始搜索点为中心,建立一个立方体,将该立方体的八个顶点作为第一次迭代的样本点,分别计算其函数值。
3)判断是否搜索到更优点。将上一步得到的八个样本点函数值进行统计,如果其中有一点的函数值比中心初始搜索点的函数值更优,则记为找到下一个搜索初始点,重新回到步骤2)进行下一步搜索。否则,进行下一步。
4)改变搜索步长。增大搜索步长,在更大的搜索范围内进行搜索,如果找到更优点,回到步骤2)。如果还没有找到更优点,进一步增大搜索步长,直至搜索步长超过一定值,停止搜索。
通过这样一种全局与局部优化算法组合的方法,结合了两种优化方式的共同优点,兼顾了全局性和精确性,其精度能达到10-5。
5.3 覆盖区求解策略
在解决给定纵程下的最大横程问题后,为了求出完整的覆盖区,需要首先找到最大纵程,然后在最大纵程轨迹上选取不同的纵程点,分别应用给定纵程下的最大横程求解方法,结合混合优化算法进行优化搜索,从而求得最大横程以及所对应的终端点,将所有的终端点连起来,就获得了再入覆盖区。由于混合优化算法在快速性和准确性上的优势,即使选取较多的纵程点,也不会影响覆盖区的求解效率,从而可以快速地获得飞行器的精确覆盖区。
6 仿真结果
飞行器基本参数:质量37 362.9kg,参考面积149.388m2,最大允许热流率为794 425W/m2,最大允许动压为14 364Pa,最大允许过载为6 gn,攻角α变化范围为 [0°,45°];马赫数Ma 变化范围为 [3,25];高度变化范围为 [0km,120km]。最大升阻比在1~1.4之间,随马赫数的增加,升阻比减小;在正攻角情况下,升阻比随攻角增大先增大后减小;最大升阻比出现在8°~10°攻角附近。仿真初始条件和终端条件如表1所示。

表1 仿真初始条件与终端条件Tab.1 Initial and terminal conditions of simulation
先给出在给定纵程为9 871.1km 时的最大横程问题的仿真结果,给定纵程下的对应左右两边各有一个最大横程,且由于受地球自转的影响,右边横程大于左边横程,图3是左右两条轨迹的最优滚转角控制曲线。由于存在滚转角约束,在超过最大约束值时,取最大约束值;在速度5 000~8 000m/s左右,约束起作用,如图4所示。图5是再入轨迹,很好地满足了热流、动压和过载的约束,图6是航迹倾角。

图3 滚转角控制曲线Fig.3 Bank angle profile

图4 存在过程约束时的滚转角曲线Fig.4 Bank angle profile with path constraint

图5 速度-高度轨迹曲线Fig.5 Velocity-altitude trajectory

图6 航迹倾角变化曲线Fig.6 Flight path angle profile
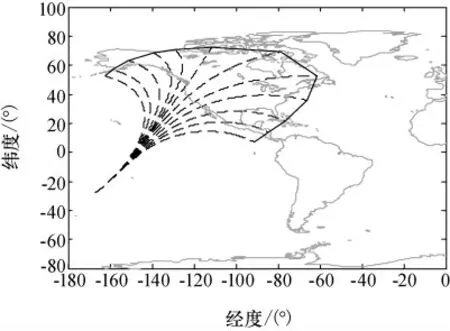
图7 覆盖区Fig.7 Footprint
在最大纵程上取多个点(这里取6 个点,如果要进一步提高覆盖区的精度,可以选取更多的点),然后对每一个纵程求最大横程,把每个横程的终点连起来,就得到了飞行器的覆盖区,如图7 所示。可以看到,右半部分要比左半部分大,这是由地球自转所导致的。
[1]VINH N X.Optimal trajectories in atmospheric flight[M].New York:Elsevier Scientific Publishing Company,1981.
[2]AMITABH SARAF,JAMES A LEAVITT,KENNETH D MEASE.Landing footprint computation for entry vehicles[C].AIAA Guidance,Navigation,and Control Conference and Exhibit,Providence,Rhode Island,2004.
[3]雍恩米,唐国金,陈磊.高超声速无动力远程滑翔飞行器多约束条件下的轨迹快速生成 [J].宇航学报,2008,29(1):46-52.YONG ENMI,TANG GUOJIN,CHEN LEI.Rapid trajectory planning for hypersonic unpowered long-range reentry vehicles with multi-constraints[J].Journal of Astronautics,2008,29(1):46-52.
[4]HALE JR N W,LAMOTTE N O,GARNER T W.Operational experience with hypersonic flight of the space shuttle:Proceedings of 2002 AIAA Guidance,Navigation,and Control(GN&C)Conference,AIAA,Orlando,FL,2002 [C].
[5]SHEN Z J.On-board three-dimensional constrained entry flight trajectory generation [D].Ames:Iowa State University,2002.
[6]LU P,XUE S B.Rapid generation of accurate entry landing footprints[J].Journal of Guidance,Control and Dynamics,2010,33(3):756-767.
[7]T B JOHN.Survey of numerical methods for trajectory optimization [J].Journal of Guidance,Control and Dynamics,1998,21(3):193-207.
[8]LU P.Entry trajectory optimization with analytical feedback bank angle law [C].AIAA Guidance,Navigation and Control Conference and Exhibit,Honolulu,2008.
