基于失真敏感性的可见光遥感图像压缩补偿

杨凯 姜宏旭

（北京航空航天大学计算机学院，北京 100191）

1 引言

随着传感器分辨率的提高，成像数据量呈几何级数增长，而星载系统传输带宽却相对有限。海量遥感数据与有限带宽的矛盾日益突出，已成为制约遥感技术发展的瓶颈。因此，遥感图像高倍有损压缩不可避免。然而高分辨率可见光遥感图像纹理细节表达丰富，景物目标分布情况复杂，高倍有损压缩后，容易出现失真的不均衡现象，影响图像整体视觉效果和后续判读应用。

对于静态图像压缩的失真补偿主要利用图像恢复技术解决。文献［1］利用改进的隐马尔可夫树模型拟合图像小波系数的分布，将其作为先验信息进行图像恢复。文献［2］针对图像压缩中的振荡现象，提出一种基于小波变换的K 邻域平均法，有效地消除了图像灰度边缘的锯齿状振荡，降低了小波压缩的Gibbs效应。这类方法仅针对失真图像建立退化模型，并未对原始图像的数据及真实的压缩失真数据进行分析，因此补偿常常无法恢复实际像质，容易出现错补偿。同时，现有的图像补偿研究主要集中于减少像素失真的绝对误差［3－4］，即提高恢复图像的峰值信噪比（Peak Signal to Noise Ratio，PSNR）值，针对改善恢复图像主观感受的补偿研究很少，由于像素的绝对误差与主观失真感受之间存在明显差异，因此现有方法对像质的改善常与主观感受不相一致。

本文针对高分辨率可见光遥感图像压缩的失真进行了深入的分析，构造了适合遥感压缩评价的失真敏感模型，在此基础上结合遥感压缩失真数据的分布特点及其对恢复像质的影响，设计实现了基于失真敏感性的可见光遥感图像压缩补偿方法，有效地改善了恢复图像中失真敏感区域的像质。

2 失真敏感性模型

由于人类视觉系统的特点，人眼对于不同特点图像区域中不同程度的数据损失感受不同。因此，要针对压缩恢复图像失真敏感区域进行补偿，需要分析人眼对真实失真数据的敏感程度，寻找与人眼失真感受相吻合的描述模型。图像压缩品质的评价，本质上就是对于恢复图像失真程度的描述。因此，可以利用评价模型作为失真敏感程度的度量标准。

结构相似度（Structure Similarity，SSIM）是目前基于人眼视觉系统（Human Visual System，HVS）的客观评价方法的代表，它认为HVS的主要功能是提取图像和视频中的结构信息［5］。其核心函数定义为

式中 x，y分别是原始图像信号和失真图像信号；l（x，y）是亮度比较函数；c（x，y）是对比度比较函数；s（x，y）是结构比较函数；α＞0，β＞0，γ＞0是权重因子。根据文献［5］的研究，SSIM 的评价效果优于大多数客观评价方法，与人眼失真感受更为接近。

当前SSIM 的研究主要基于对自然景观图像不同类型失真的分析，对可见光遥感图像压缩失真的评价针对性不足，为此本文深入研究了结构相似度对于遥感压缩失真的评价效果。首先，构造了可见光遥感图像压缩失真图像库。选择以遥感图像为主的10幅不同复杂程度的测试原图像，采用5种不同原理的压缩算法（JPEG，JPEG2000，FACTRAL，HD－PHOTO，BPP）［6－8］，分别按照不同压缩位率压缩并恢复，构成具有250幅不同图像特征和失真特点图像的测试库，并挑选5名图像判读员采用双刺激方法对失真图像打分，加权得到主观质量评分（Mean Opinion Score，MOS），详细建库过程可参考文献［9］。在此基础上，对SSIM 和PSNR 的评价效果进行了比较。根据多种相关性度量指标的对比发现，SSIM 与MOS的一致性比PSNR 更好［10］。因此，可以认为，使用SSIM 作为评价模型寻找遥感图像压缩失真敏感区域时，可以取得比以PSNR为代表的客观评价方法更好的结果。

为更加准确地定位失真敏感区域，本文进一步将SSIM 核心函数中的l（x，y）、c（x，y）、s（x，y）及l（x，y）c（x，y）、l（x，y）s（x，y）、c（x，y）s（x，y）与MOS的相关程度进行了分析。表1是各函数与MOS的相关性度量，其中Pearson相关系数（Correlation Coefficients，CC）和Spearman秩相关系数（Spearman Rank Order Correlation Coefficient，SROCC）值越大表示函数与MOS相关程度越高。由表1可知，c（x，y）与MOS的相关性最大，即c（x，y）与人眼对压缩失真的评价最一致。因此，在对遥感图像压缩失真进行评价时，使用c（x，y）函数代替SSIM（x，y）更为合适。

表1 各函数与MOS的相关性度量Tab.1 Correlations of MOS and SSIM component functions

根据人眼视觉敏感性的特点和遥感图像判读的标准可知，背景亮度会对失真的敏感程度产生明显影响。因此，本文构造图像区域平均亮度的函数f（L）＝m（L（x））n（其中L（x）为图像x 的平均亮度；m、n为权重因子）作为评价模型c（x，y）的权值，最终得到图像区域失真敏感性模型，记为cSIM。

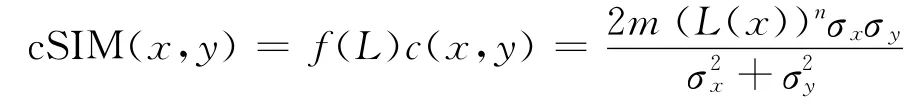
为比较失真敏感模型的定位效果，本文选择5幅512像素×512像素遥感图像进行12倍压缩，将原始图像与失真图像分块计算cSIM 值，依据cSIM 值标定失真最为明显的32个图像块，cSIM值越小（失真越明显），块亮度越大。挑选2名判读人员对比失真图像和原始图像，判读主观失真感受明显区域。结果发现，cSIM 选定区域与主观失真明显区域基本吻合（如图1所示），可以认为使用cSIM 值作为失真敏感度量是恰当的。

图1 失真敏感定位显示Fig.1 Location of distortion sensitivity

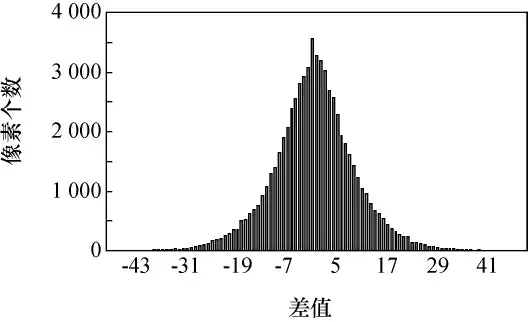
图2 差值柱形分布Fig.2 Histogram of image distortion

3 基于失真敏感性的补偿

失真的感受是对图像空域数据丢失的敏感，常见的补偿方法主要依据恢复图像数据求取滤波器参数，容易出现错补偿，造成像质的进一步下降。因此，本文设计了对图像空域差值数据压缩回传的策略用于补偿恢复。

为保持固定的压缩位率，需要对差值数据进行有损回传。分析原始图像与恢复图像的差值分布（如图2所示）可以发现，图像差值主要集中于零值，差值较大的数据较少，近似于正态分布。根据HVS的特点可知，人眼对非常小的像素值变化感受并不明显，而差值较大数据又因其所处位置对失真感受有不同影响。本文将原始图像进行边缘提取（见图3（a）），比较不同大小的差值在图像中所处的位置，发现差异最大的数据主要集中于边缘等对比度变化明显的像素突变处（见图3（b））且数量较少，由于掩蔽效应不易被察觉；差值介于几至几十之间的数据丢失数量众多，又常位于图像纹理细节、暗弱目标处（见图3（c）），容易被分辨造成失真感受，影响判读。因此，本文设计补偿策略时仅对易感数据有损量化回传，过大或过小的差值均进行相应的量化处理。

图3 差值分布位置比较Fig.3 Comparision of image distortion distribution

对多幅图像的差值分布图分析发现，纹理复杂、压缩倍数高的图像差值分布更为平缓、分散，纹理简单、压缩倍数低的图像差值分布更为集中。因此，具体的量化值设定应更为自适应。综合多幅图像补偿的对比效果和后续位平面熵编码的原理，将差值数据量化至3个位平面。假设图像差值数据为正态分布，定义分布密度函数为

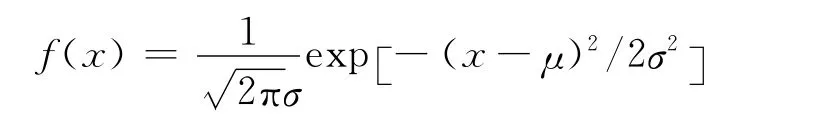
令μ＝0，x′＝x／σ化为标准正态分布，其分布密度函数为分布函数为

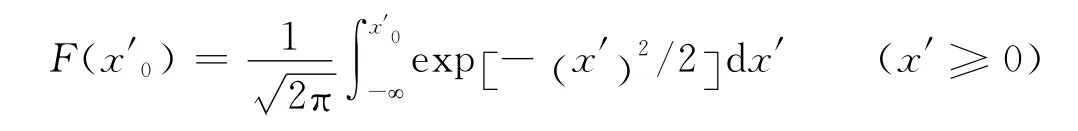
则P｛｜x｜≤Δ｝＝P｛｜x′｜≤σΔ｝＝F（σΔ）－F（－σΔ）。

若令ε＝0.95，求F（x′）的α分位点。令α＝0.5，用ZP表示F 的P 分位点，则x′＝Z1－α／2，可得x＝σZ1－α／2＝1.96σ。

4 试验与分析

根据以上基于失真敏感性补偿的思想，本文实现了一个结合图像补偿的遥感图像压缩算法，算法在固定位率压缩的编码端计算恢复图像的失真敏感区域，量化并回传敏感区域失真数据供解码端补偿。具体操作步骤如下：

1）原始图像X 进行固定位率Q 编码时，预留码流空间q，仅编码Q－q并记录编码截断点；

2）将截断点前小波系数反变换为恢复图像Y，并对图像X 和Y 进行多尺度分块，分别记为X＝｛xi｜i＝1，2，…，N｝和Y＝｛yi｜i＝1，2，…，N｝；

3）计算各cSIM（xi，yi）并依据排序确定失真敏感优先级；

4）依据优先级求取差值数据Di，并依据本文上一节所述方法量化为D′i，连同位置信息一起送入编码器编码长度为q的码流；

5）解码时，将回传补偿数据依据位置信息补偿到恢复图像的对应位置，实现像质改善。

为比较本方法的补偿效果，本文在相对性能最好的自有遥感图像压缩算法BPP［8］的基础上，将本文方法进行实现（记为cBPP），并用5幅可见光遥感图像进行试验对比。图像数据均来源于网络，图像尺寸为512像素×512像素，压缩倍数分别设为8、12、16倍，编码预留的补偿空间设为压缩码流的压缩倍数分之一。最终结果由2名判读员通过主观判读，对比cBPP 算法恢复图像与BPP恢复图像获得（见表2）。由表2 可知，与BPP 相比，cBPP 算法明显改善或相当的比例为83.33%，因此在不同压缩倍数下，加入补偿方法的cBPP算法能够有效改善大多数图像的主观质量。同时，由于预留码流空间的原因，部分图像会由于其他区域的失真造成像质的明显下降。

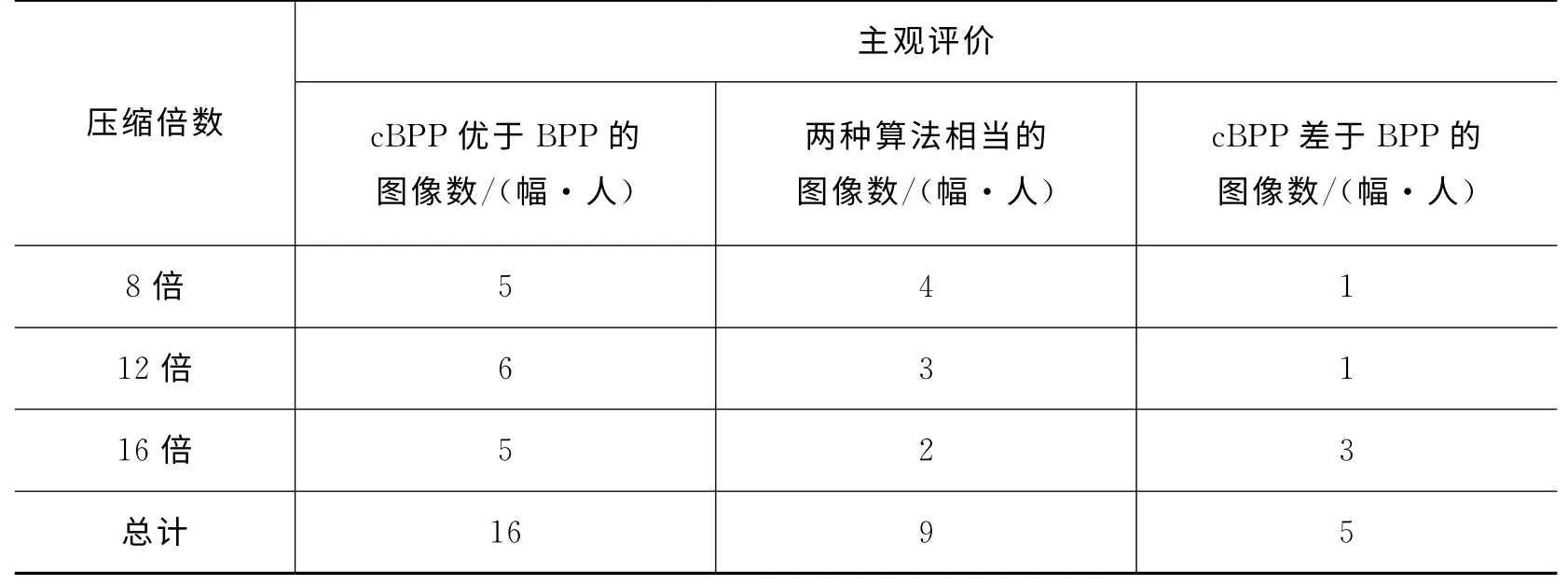
表2 主观对比结果统计Tab.2 Subject comparison statistics

图4为某原始图像、BPP算法12倍压缩恢复图像及cBPP算法恢复图像的部分对比显示。对比图4可以发现，cBPP算法在预留部分码流空间后并未对图像总体质量产生明显影响，而由于局部的补偿作用，图4（c）总体感觉比图4（b）清晰。对比局部放大图可见，图4（e）中两辆车辆已模糊不清，马路边缘也明显抖动甚至消失，而图4（f）中车辆仍清晰可见，车头处的车窗仍能辨识，马路边缘亦较为清楚，无明显形变；图4（h）中的小目标已模糊丢失，马路边缘明显模糊，而图4（i）中小目标与图4（g）相比虽已出现模糊但仍能辨别，马路边缘清晰笔直，无明显失真。

图4 恢复图像主观对比Fig.4 Subject measure of images

5 结束语

本文针对遥感图像高倍有损压缩后恢复图像局部失真影响图像整体品质的问题，构造了有效的压缩失真敏感性模型，设计了基于失真敏感性可见光遥感图像的压缩补偿方法，实现了对遥感图像局部明显失真的有效补偿。该方法研究过程中更加侧重图像主观品质的恢复，在失真敏感模型的建立、量化策略的选择和恢复质量的评价等过程中，均进行了相应的主观判读分析。同时必须说明的是，主观评价方法虽然能够真实反映人眼感受，但其本身易受判读员及观察环境等影响，且不便于数学定量描述，因此本方法的研究亦存在相应的局限。下一步工作的重点将侧重于失真敏感性模型的预测计算、补偿方式的改进以及主观评价定量描述等方面。

［1］FAN GUOLIANG，XIA XIANGGEN.Wavelet－based texture analysis and synthesis using hidden Markov models［J］.IEEE Transactions on Circuits and Systems I：Fundamental Theory and Applications，2003，50（1）：106－120.

［2］赵晨萍，郭运瑞，李登峰，等.一种基于K 邻域平均法的小波图像恢复算法 ［J］.现代电子技术，2009，32（2）：148－150.ZHAO CHENPING，GUO YUNRUI，LI DENGFENG，et al.Algorithm of wavelet image recovery based on K neighborhood average method ［J］.Modern Electronic Technique，2009，32（2）：148－150.

［3］JAVIER MATEOS，TOM E BISHOP，RAFAEL MOLINA，et al.Local Bayesian image restoration using variational methods and Gamma－normal distributions ［C］.16th IEEE International Conference on Image Processing（ICIP），Granada，Spain，2009.

［4］BAO QIANGZONG，LI QINGCHUN.Image restoration with significant curvelet coefficients index set constrains［C］.2010 IEEE International Conference on Information Theory and Information Security（ICITIS），Xi′an，2010.

［5］WANG ZHOU，ALAN CONRAD BOVIK，HAMID RAHIM SHEIKH，et al.Image quality assessment：from error visibility to structural similarity ［J］.IEEE Transactions on Image Processing，2004，13（4）：600－612.

［6］YUVAL FISHER.Fractal image compression：theory and application［M］.New York：Springer－Verlag，1995.

［7］THE INTERNATIONAL TELEGRAPH AND TELEPHONE CONSULTATIVE COMMITEE.Information technology－digital compression and coding of continuous－tone still images［S］.British Standards Institute，Draft International Standard ISO／IEC 10918，1992.

［8］焦润海.图像压缩中的高效预测编码及其优化实现技术 ［D］.北京：北京航空航天大学，2008.JIAO RUNHAI.High efficient prediction coding and its optimization in image compression ［D］.Beijing：Beihang University，2008.

［9］文义红，杨凯，李波.静态图像压缩评估方法测评 ［J］.中国空间科学技术，2010，30（1）：72－77.WEN YIHONG，YANG KAI，LI BO.Performance test for image quality assessment［J］.Chinese Space Science and Technology，2010，30（1）：72－77.

［10］YANG KAI，JIANG HONGXU.Optimized－SSIM based quantization in optical remote sensing image compression ［C］.Sixth International Conference on Image and Graphics（ICIG），Hefei，2011.