第13届亚洲物理奥林匹克竞赛实验试题简介

杨 景，荀 坤，陈晓林

（北京大学物理学院，北京100871）

1 引 言

第13届亚洲物理奥林匹克竞赛于2012年5月1日至5月8日在印度首都新德里举行.代表中国参赛的8名中学生全部都获得了金牌，并且包揽了总分前三名.其中姚文杰同学还获得了总分第一和实验第一的好成绩，而刘尚同学则获得了理论第一的好成绩.

本届竞赛的2道实验题分别是“摩擦系数”和“电磁感应”.因原题较长，我们不得不作缩略，但会尽可能保留原貌.试题解答采用赛会提供的标准答案，并在必要时作简短评论.

2 试 题

2.1 试题1：摩擦系数

图1 摩擦系数实验示意图

由于摩擦力的作用，绕过圆柱的细绳的两端张力会不同（见图1）.要拉住细绳一端悬挂的物体，在细绳另一端加的力可以比物体所受的重力小.随着细绳在圆柱上缠绕圈数的增多另一端所需加的最小力会以令人吃惊的速度减小.基于此，水手在固定船只时会将缆绳在泊桩上绕很多圈.本实验拟系统地探究负载W（＝MWg）、最小平衡力P（＝MPg）及缠绕角θ三者之间的关系.

2.1.1 实验装置

实验装置如图2所示.在平台的中间竖立一钢管，在其四周各平置一钢管.在其中一平置钢管前，放一有机玻璃刻线板（间距为1.5mm），用于检测细绳是否移动.用来缠绕钢管的绳子有花色和粉色2种.在绳子的两端可分别悬挂塑料秤盘和重物.放大镜上的蓝色滑块用于开关照明灯.含挂架的塑料秤盘的质量Mpan标在秤盘的侧面，秤盘内可放置不同质量的砝码，计有500.0，200.0，100.0，50.0，20.0，10.0，5.0，2.0，1.0g等规格.1个质量未知的物体，其质量用Mu表示.1个带挂钩的重物串，每件质量均为100g，总质量为800g.

图2 摩擦系数实验装置图

2.1.2 实验任务

1）研究负载W、最小平衡力P以及缠绕角θ之间的关系（注：在此部分使用花色绳）.

以带挂钩的重物串作负载MW，将其系在所给花色绳（其质量可忽略）一端，并在绳的另一端系上秤盘（质量已知）.通过使细绳跨过或绕过2个或更多个钢管可以改变缠绕角θ（见图3）.平衡力由秤盘和加在其中的砝码提供.

当细绳不接触竖直钢管横跨在2个平行钢管上时得到的缠绕角θ最小（见图3）.通过使细绳绕过竖直钢管，及将秤盘和砝码挂放在不同的水平管上，可使缠绕角θ以π／2的步长变化.负载应放置在装有刻线板的水平管一侧.

理论上，可以通过观察MW相对于刻线板移动的临界状态来确定MP（克服静摩擦力）.但实际上只能确定该值所处的区间[MP－，MP＋].测量时应使该区间尽可能小.

图3 缠绕角分别为π和3π／2的示意图

a.固定θ角，研究MP与MW的关系.（2.2分）

在θ＝π时，改变负载，测量不同负载时MP的大小.要利用所给砝码使测量范围尽可能宽.要估算测量值包含因子为2的扩展不确定度.画图确定MP与MW之间的关系.

b.固定负载MW，研究MP与θ之间的关系.（5.2分）

改变θ角度，测量平衡时MP的值.画出必要的图线，综合各图线得到MP与θ之间的关系.

c.综合各图线得到所需的方程.（0.6分）

分析所得数据，将P用W和θ表达出来.P的表达式中还会含有与钢管和细绳间的摩擦有关的项.从P的表达式中找出此项，令其等于系统的摩擦系数μ，并估算此系数的扩展不确定度.

2）测量未知物体质量Mu和粉色绳与钢管之间的摩擦系数μu.（2分）

写出用以求得Mu和μu的方程.利用任务1）中得到的关系式，在θ＝π时作必要的测量来确定未知重物的质量Mu以及粉色绳与钢管之间的摩擦系数μu，并估算它们的扩展不确定度.

2.2 试题2：电磁感应

2.2.1 引言

在1个耦合线圈系统中（2个线圈），通过线圈1磁通量为φ1＝L1i1＋M12i2，式中，i1和i2分别为流过线圈1和线圈2的电流，L1是线圈1的自感系数，M12是互感系数.当线圈2通有电流时，磁通量与上式类似，并有M21＝M12＝M.

当角频率为ω的交流电流过串联的电阻R和电感L时，会有电压降.设电流i＝I0sinωt，则电阻和电感上的电压降分别等于I0Rsinωt和I0ωLcosωt，ωL称为感抗，用符号X表示.称

为总阻抗.可以将R和L上的总压降表示为I0Zsin（ωt＋θ），其中

交流电压和交流电流的有效值V和I满足类似于欧姆定律的表达式：V＝IZ.由此有

不同于直流电路中电阻由欧姆定律来决定，交流电路中电阻的概念是与电磁能的耗散相联系的.

若电路中还有其他电阻或电感与L和R组合串联，回路中的总电压降等于总电阻上的电压降和总电感上的电压降平方和的平方根.

由式（2）和（3）可以得到：

如果在1个含有线圈和1个已知电阻R′的组合回路上，加上电压VA（如图4所示），那么电压VA和R′上的电压降VR′，线圈上的电压V和角度θ的关系为

式（6）中除θ外的所有量都能够测量得到.

图4 测量线圈感抗和电阻的电路图

因此，测量出3个电压VA，VR′和V，并利用式（4）～（6），θ，R，Z和X就能够被确定：

若知道交流电的频率，则还能够计算出L.

对于由2个线圈组成的耦合回路，电源供给初级线圈的能量，部分消耗在初级线圈中，部分消耗在与之耦合的次级线圈中.当不存在机械功时，能量仅消耗在电阻上.电感不耗能，只是将电能以磁能的形式储存起来.对于自感系数为L的电感，当电流为I时，其平均储能等于LI2／2.

当电流流经次级线圈时，其在初级线圈中感应出的电动势会导致初级线圈中的电流变化.可以将次级线圈的影响包含在初级线圈的等效电阻和等效感抗中，使初级和次级线圈中消耗的总能量就好像是消耗在初级线圈的有效电阻上一样.

初级线圈等效电阻RPE和等效电感LPE与从次级线圈“反射”的电阻RR和“反射”的电感LR有关.在初级线圈中，反射的电阻RR所消耗的（平均）功率必须等于次级回路中电阻RS消耗的功率，即

类似地，反射的电感LR和次级回路中电感LS满足：

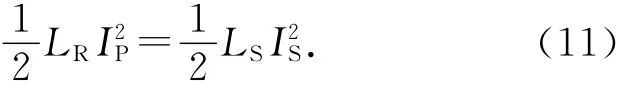
由于初级线圈中交变电流IP的改变，而在次级线圈中感应电动势的大小等于ωMIP.根据基尔霍夫回路方程，可以写出初级和次级线圈中电流满足的方程式中ZS是次级回路中的总阻抗.当次级回路中阻抗为无限大时，感应电动势就好像作用于开路的次级线圈上.

2.2.2 实验装置

实验装置如图5所示.频率1 000Hz时输出为10V（有效值）的正弦波发生器；数字万用表；2组绕在同一个无磁性非导体圆柱状中空绕线筒上的同轴耦合线圈；能够插入中空绕线筒的铝棒；安装在绝缘板上的电阻排（每排10个电阻：其中一排的电阻值均为100Ω，另一排的则均为10Ω，都含有香蕉插孔）；所需要的负载电阻RL或者取样电阻R′可以用电阻排和导线连接来进行选取，当电阻排用作负载电阻时，还有另一个300Ω的电阻可用作取样电阻；带香蕉插头的5根黑线和5根红线.

频率为1 000Hz的正弦波发生器可用于产生交流电压.使用万用表的20V量程测量交流电压的有效值.若有需要，可以从测量到的初级回路中R′上的电压和次级回路中RL上的电压，计算得到电流IP和IS.

图5 电磁感应实验装置图

2.2.3 实验任务

1）测量无芯（空气芯）线圈和铝芯线圈的电阻和电感.（3.4分）

如图6所示，将线圈1（接线柱为蓝色）和电阻R′（从电阻排上取）串联，并连接到正弦信号发生器的两端.

交换连接数字万用表的“V／Ω”和“com”插口的表笔得到的读数会有些许不同，每次测量时都要交换万用表的表笔，并取2次测量值的平均.

请选适合的R′，使VR′和V值大致相等.这样，电压测量的系统误差对阻抗Z的影响可忽略.

图6 测量线圈电阻和电感的电路图

a.测量VA，VR′和V，以及另一线圈两端的电压VO，得到线圈1（蓝色端点）的电阻R1和电感L1，并估算测量值的不确定度.（0.9分）

b.连接线圈2（接线柱为绿色），通过测量确定R2和L2.估算测得值的不确定度.（0.9分）

c.将铝棒插入线圈中，重复a.，找出线圈1的电感L＊1和电阻R＊1及相应的不确定度.（0.8分）

d.重复b.，得到带铝芯的线圈2的电感L＊2和电阻R＊2，并估算不确定度.（0.8分）

下面第2），3），4）部分，不需计算不确定度.

2）互感和耦合常数.（3分）

e.互感M可以从VR′和VO[在1）部分中已测量]中得到.分别给出不带和带铝芯的线圈1和线圈2的互感的平均值.耦合线圈的互感和自感之间的关系由M＝k（L1L2）1／2给出.确定耦合常数k的值.（0.4分）

f.如图7所示，用线圈1（蓝色接线柱）作初级线圈，线圈2（绿色接线柱）作次级线圈.将初级线圈与取样电阻R′＝300Ω串联，并接于信号发生器的输出端.将次级线圈与可变电阻RL相联.测量RL两端的电压以得到输出电压VO.改变RL，测量每个RL时的VA，VR′，V和VO.（0.8分）

g.将式（12）重写成展开式，可作出线性图.其斜率可用来获得互感M，截距可用来获得次级线圈的感抗XS.给出线性图的表达式.（0.2分）

h.使用f.中的数据，算出一些必要的物理量，并画出对应于g.中表达式的图.（0.9分）

i.作图，并得到M和XS的值.（0.7分）

3）初级线圈的等效阻抗和次级线圈的反射物理量之间的关系.（2.4分）

j.使用2）中得到的数据，找出对应次级回路中各个RL取值时，初级线圈的等效电阻RPE和等效感抗XPE.（0.6分）

图7 测量线圈互感的电路图

k.使用2）中得到的数据，对所有RL，计算式（10）中所定义的反射电阻RR和反射电抗XR[参见式（11）].（0.6分）

l.作出XPE随XR变化的曲线.请考虑作图所绘各量的不确定度，写出初级线圈的等效感抗和反射感抗之间关系的表达式.（0.6分）

m.在所研究的取值范围内，用图像表示出RR和RL的关系，并找出反射电阻达到最大时RL的取值.如有需要，可进一步测量得到更多数据，以便更加精确地找出上述最大值.（0.6分）

4）涡流效应.（1.2分）

n.通过分析3）中得到的数据，可以使用一种模型来估算金属芯中的涡流所感受到的电感和电阻的比值.通过分析2）中h.和i.的数据，可以得到RPE＝RP＋RR.而XPE和XR之间的关系从3）中l.得到.参照1）中c.得到的数据，分别对线圈1和线圈2接上电源的情形，估算铝芯中涡流所感受到的电感和电阻的比值.（0.8分）

o.按照2）中图3所示连接线圈，并插入铝芯.给出铝芯的功率损耗ΔP的表达式.取R′＝300Ω，RL＝1 000Ω，将VA调到9.0V.通过测量，得出铝芯中涡流引起的功率损耗.（0.4分）

3 试题解答

3.1 试题1解答

3.1.1 研究负载W、最小平衡力P以及缠绕角θ之间的关系

a.按图3（a）的方式固定θ＝π，测量在不同的负载MW下，达到平衡时所需的MP值，测量数据见表1.

表1 MP与MW的关系测量数据（θ＝π）

表1中的测量数据点如有4个得0.4分，每多测1个数据点多得0.1分，测满8个数据点得0.8分.如有5个数据点的不确定度ΔMP＜5g得0.4分，每增加1个不确定度ΔMP＜5g的数据点多得0.1分，全部数据点的不确定度＜5g得0.7分.在MW＞500g时，若ΔMP＜1g，不得分.

作图区域占据作图纸的70%以上得0.1分.如有3个点在直线上得0.1分；如有4个点在直线上得0.2分.2个坐标轴单位标注正确得0.1分.图8中的直线斜率在0.6～0.8之间得0.3分，在0.5～0.6或者0.8～0.9之间只得0.1分.

图8 与MW间关系图

b.固定负载MW，研究MP与θ之间的关系.

取负载MW＝800.0g.通过使细绳绕过竖直钢管，可使缠绕角θ以π／2的步长变化.改变θ角，测量平衡时MP的值，测量数据见表2.

表2 MP与θ的关系测量数据（MW＝800.0g）

表2中测量数据点有6个或7个得0.5分；如有8个数据点得1分，在此基础上每增加1个数据点多得0.1分，直至得满1.4分.如有8个数据点的不确定度ΔMP＜5g得0.8分，每增加1个不确定度ΔMP＜5g的数据点多得0.1分，直至得满1.2分.但不确定度ΔMP＜1g不得分.

作图区域占满作图纸的70%以上得0.2分.2个坐标轴单位标注正确得0.2分.曲线平滑得0.6分；如曲线大体平滑（至少有一半数据点在曲线上）得0.4分.

图9 MP与θ间关系图

c.综合所得实验结果，得到P，W和θ的关系表达式.为了验证上述指数衰减关系，可以作ln MP－θ或者ln（MP／MW）－θ图.如果二者成线性关系，就表明

或者

结合所得的关系（13）和（14），可得到

常数k可以定义为摩擦系数μ，

考虑到θ＝0时，P＝W，常数C为1.因此可以得到P，W和θ之间的关系：

作ln（MP／MW）－θ图，如图10所示.由图10的斜率得到μ＝0.106.根据ΔMP可得到Δμ＝0.011，换算成标准差uc（μ）＝0.006 2.扩展不确定度U（μ）＝0.012≈0.01.因此μ＝0.11±0.01.

图10 ln（MP／MW）与θ间的关系曲线图

图10中作图区域占满作图纸的70%以上得0.2分.坐标轴单位标注均正确得0.1分.有4个点在直线上得0.4分，5个点得0.5分，6个点得0.6分.图10中的斜率在0.09～0.13之间得0.5分，在0.08～0.09或者0.13～0.14之间只得0.4分.斜率的不确定度计算方法有0.1分，扩展不确定度小于等于0.02再得0.1分.能将式（17）中θ前的系数确定为摩擦系数μ得0.1分.式（17）正确得0.5分.式（17）中将重量P和W混淆成质量MP和MW只能得0.2分；常数C没有判断为1的也只能得0.2分.

3.1.2 测量未知物体质量Mu和粉色绳与钢管之间的摩擦系数μu

将未知重物Mu和秤盘MP分别悬挂于粉色绳的两端（缠绕角θ＝π），在秤盘内加入砝码使粉色绳静止.当秤盘达到向上运动和静止间的临界状态时，摩擦力阻碍未知重物下落，

当秤盘达到向下运动和静止间的临界状态时，摩擦力阻碍秤盘下落，

分别测量秤盘向上和向下2种临界状态时的质量MP.秤盘处于向上临界状态时，MP1的范围为73.6～77.6g.秤盘处于向下临界状态时，MP2的范围为184.6～192.6g.

Mu的不确定度计算为

μu的不确定度计算为

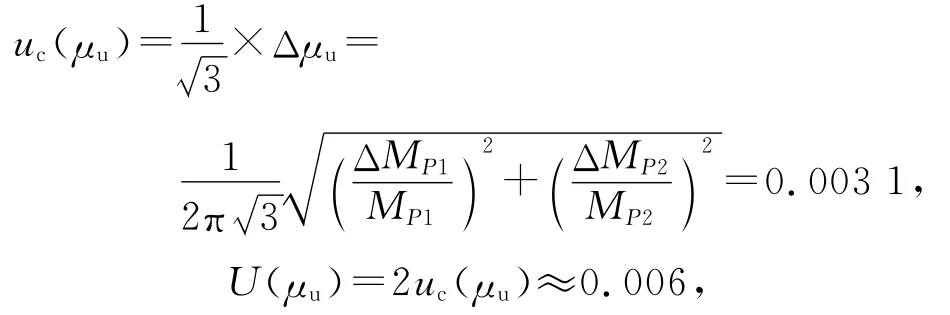
求解式（18）和（19）正确得0.4分，测量Mu和μu的方法正确得0.6分.测量[MP1－，MP1＋]和[MP2－，MP2＋]得0.4分.Mu的值在115～121g之间得0.2分，如在113～115g或121～123g之间只能得0.1分.Mu的扩展不确定度≤4g得0.1分.μu的值在0.13～0.20之间得0.2分，μu的扩展不确定度≤0.01得0.1分.

3.2 试题2解答

3.2.1 测量无芯（空气芯）线圈和铝芯线圈的电阻和电感

按照图6，分别测量VA，VR′和V，根据式（7）和（9），得到线圈的电阻和电感.分别对a.线圈1空气芯、b.线圈2空气芯、c.线圈1铝芯和d.线圈2铝芯共4种情况进行测量，测量数据见表3.

表3 电压测量数据

根据前面的公式计算出线圈参量，得到表4.

表4 线圈参量数据

这一部分实验内容要求计算不确定度.此处实验的测量过程是用数字万用表对电压进行测量，因此系统误差由万用表说明书给出.在20V量程范围内，万用表电压挡的系统误差ΔV＝±（1.0%×读数＋4个字）.表1中ΔVA，ΔV和ΔVR′的数值即据此得到.ΔV看作是极限误差，按照均匀分布规律换算成标准差us（V）＝ΔV／除此之外，还要求考虑数字万用表的分辨率误差，即读数最后一位的半值.由于测量在20V量程范围内，最小分度为10mV.因此分辨率带来的标准误差为ur（V）＝0.005／＝0.002 9V.由式（7）及（8）可以进行误差计算，得到R的系统误差us（R）和分辨率误差ur（R）及Z的系统误差us（Z）、分辨率误差ur（Z）.最后得到的合成误差为和uc（Z）＝通过公式X2＝Z2－R2可以得到感抗误差uc（X）和电感误差uc（L）.最后的误差结果要求用包含因子为2的扩展不确定度来表达，即U（R）＝2uc（R）和U（L）＝2uc（L）.误差计算结果见表5.

表5 误差计算结果

对上述4种情况的测量，即：a.线圈1空气芯、b.线圈2空气芯、c.线圈1铝芯、d.线圈2铝芯，评分标准基本一样.首先要求选择适当的R′，使得｜V－VR′｜≤0.15V.这样可以减少电压测量给阻抗Z带来的系统误差.满足上面的要求，a～d每一种情况各得0.1分，共0.4分.

其次对于空气芯线圈的测量a.和b.，交换电表探头测量电压2次，a.和b.各得0.2分；只测量1次各得0.1分.Z1在435～465Ω，得0.1分；R1在40～47Ω，得0.1分，L1在69～73mH，得0.1分.us（R1）在1.1～1.2Ω之间得0.1分；U（R1）为±3Ω，得0.1分；U（L1）为±0.2mH，得0.1分.Z2在335～365Ω，得0.1分；R2在40～47Ω，得0.1分，L2在52～59mH，得0.1分.us（R2）在0.85～0.97Ω之间得0.1分；U（R2）为±3Ω，得0.1分；U（L2）为±0.1mH或者±0.2mH，得0.1分.

对于铝芯线圈的测量c.和d.，评分标准与a.和b.略有不同.交换电表探头测量2次，c.和d.中各得0.1分，若只测量1次，则不得分.在280～310Ω，得0.1分；在100～110Ω，得0.1分，在42～46mH，得0.1分.us（）在1.1～1.4Ω之间，得0.1分；U（）为±3Ω，得0.1分；U（）为±0.2mH，得0.1分.在275～285Ω，得0.1分；在64～76Ω，得0.1分，在40～44mH，得0.1分.us（）在0.91～1.2Ω之间，得0.1分；若U（）为±2Ω或者±3Ω，得0.1分；U（）为±0.2mH，得0.1分.

3.2.2 测量互感和耦合常数

按照图7连接电路图，注意此处实验要求使用的是线圈1作为初级线圈，线圈2作为次级线圈，并且是空气芯的情况.改变可变电阻RL，测量VA，VR′，V和VO.将式（12）展开，

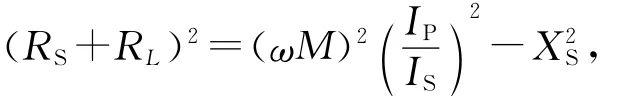
实验数据如表6所示.

测量5组数据点得0.4分，6组数据得0.5分，7组数据得0.6分.如果超过7组数据并且RL是按100Ω步长递增，再得0.1分.交换电表极性测量电压2次得0.1分.

作图所依据的公式即式（12）的展开式正确，得0.2分，计算作图参量，有4个数据点得0.2分；5个数据点得0.4分；6个数据点得0.6分.IP和IS计算正确各得0.1分，（RS＋RL）2计算正确，特别是RS应选为线圈2空气芯的电阻，得0.1分.

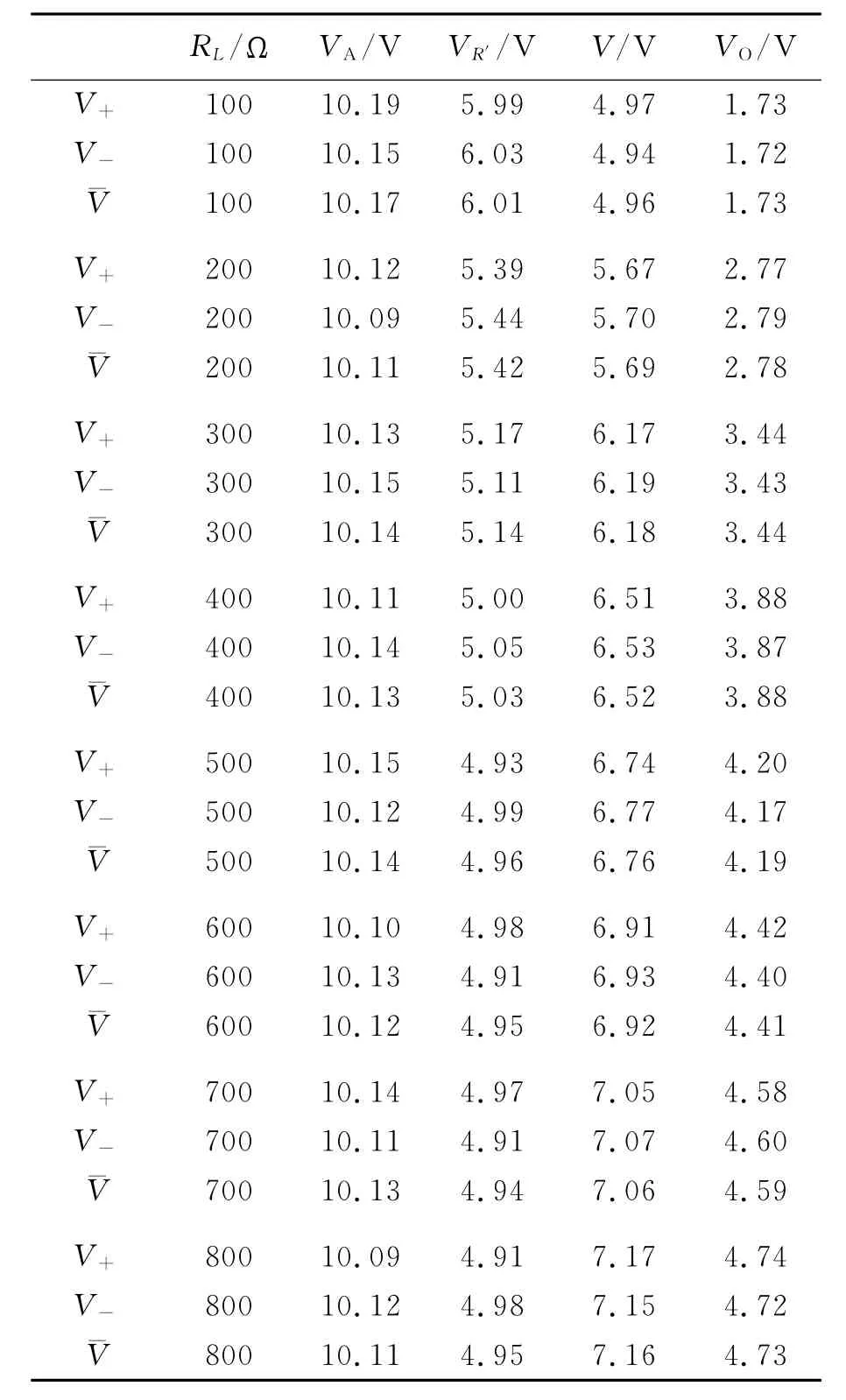
表6 改变可变电阻RL测量电压数据

表7 和作图所用参量数据

表7 和作图所用参量数据

RL／ΩIP／A IS／A（IP／IS）2（RS＋RL）2／Ω2 100 0.020 0 0.017 1.35 20 438.25 200 0.018 1 0.014 1.69 59 030.73 300 0.017 1 0.011 2.24 117 623.21 400 0.016 8 0.010 2.99 196 215.69 500 0.016 5 0.008 3.90 294 808.17 600 0.016 5 0.007 5.03 413 400.65 700 0.016 5 0.007 6.31 551 993.13 800 0.016 5 0.006 7.77 710 585.61

图11 和的关系图

作图区域占满作图纸的70%以上得0.1分.恰当地选取原点坐标得到截距，得0.1分.从斜率中计算得到的M在50～54mH范围内，得0.1分；如更精确地处在51～52mH范围内得0.2分.从截距计算得到的XS在320～385Ω范围内得0.1分；如更精确地处在335～360Ω得0.2分.如有5个点以上在直线上得0.1分.

3.2.3 初级线圈的等效阻抗和次级线圈的反射物理量之间的关系

首先要求计算等效阻抗和反射阻抗，再研究二者之间的关系.对于等效阻抗，是从初级线圈的角度出发，将次级线圈在初级线圈中产生的感应电动势等效为初级线圈阻抗的变化对电流的影响.反射阻抗是从次级回路的角度出发，将次级回路上的能量损耗根据能量守恒定律等效为初级回路中的反射阻抗.具体计算公式如（10）和（11）所示.因此直接利用3.2.2部分的电压测量数据，代入线圈阻抗计算式（7）和（9）即可得到等效电阻和等效感抗，而代入定义公式（10）和（11）即可得到反射电阻和反射感抗.注意在代入公式（10）的过程中，次级回路的电阻应为线圈的电阻RS和串联的可变电阻RL之和，即式（10）应为具体数据见表8.

表8 等效阻抗和反射阻抗随RL的变化数据

等效电阻的计算公式正确得0.1分.计算5个数据点得0.1分；计算6个及以上得0.2分.等效感抗、反射电阻和反射感抗的评分标准均与等效电阻相同.

作XPE随XR的变化曲线，得到二者成线性关系，如图12所示.观察图中直线的斜率和截距，可得斜率为－1，截距为线圈1空气芯的感抗XP.因此有关系式XP－XR＝XPE.

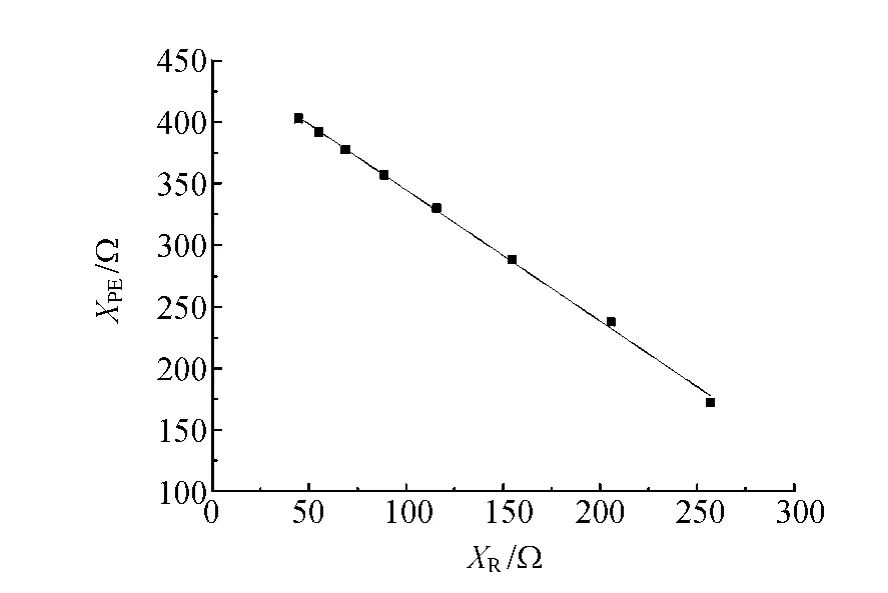
图12 XPE和XR关系图

作图区域占满作图纸的70%以上得0.1分.恰当地选取原点坐标得到截距，得0.1分.斜率在－0.9～－1.1范围内，得0.1分；截距等于第（1）部分中所测得的线圈2空气芯的感抗，误差在＋20Ω范围内，得0.1分.如有5个点以上在直线上得0.1分.推导出关系式XP－XR＝XPE得0.1分.

试题还要求研究RR和RL的关系.观察前面的测量数据，可以发现当RL＝300Ω左右时RR有最大值.进一步在RL＝300Ω附近进行细致测量，可得到反射电阻有最大值时的RL取值.此处要求作图，数据如表9所示，关系图见图13.

根据图13可知当RL＝300Ω时，RR有最大值.其实RR和RL之间的关系也可以通过推导得到.将式（12）代入（10），可得当RL＝XS－RS时，RR有最大值.

作图区域占满作图纸的70%以上得0.1分.曲线光滑得0.1分.有明显的峰得0.1分.RL在理论值（XS－RS）附近＋20Ω范围内，得0.1分；如更精确地处在±5Ω范围内得0.3分.

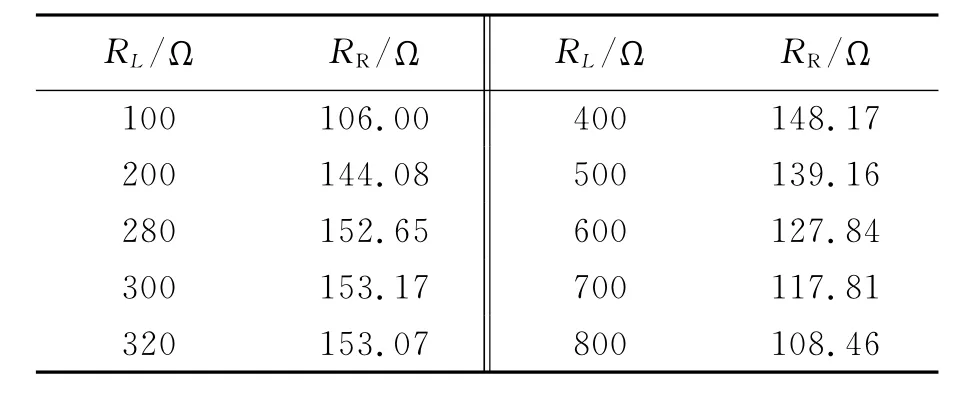
表9 反射电阻RR随可变电阻RL的变化

图13 RR和RL的关系图

3.2.4 涡流效应

此部分研究线圈中插入金属芯产生的涡流效应，测量数据见表10.首先要求估算铝芯中涡流受到的电感和电阻的比值.由式（10）和（11）之比看出：铝芯中涡流受到的电感和电阻之比等于反射电感和反射电阻之比.根据前面得到的反射阻抗和等效阻抗的关系，有分别代入线圈1和线圈2的相关参量，可得到比值4.85×10－4s和4.50×10－4s.

从等效阻抗和反射阻抗的讨论可得出，初级线圈中反射电阻消耗的功率等于铝芯损耗功率与次级线圈电阻消耗的功率之和，即ΔP＝（RPERP）－（RS＋RL）.取R′＝300Ω，RL＝1 000Ω，VA＝9.0V，通过相应的测量计算可以得到铝芯中涡流引起的功率损耗为1.65×10－2W.

表10 铝芯功率损耗电压测量数据

评分标准对物理概念、公式和数据都有要求.估算涡流所感受到的电阻和电感比值时，物理概念清晰，公式正确得0.4分，2个比值计算正确各得0.2分.计算涡流功率损耗时，交换万用表探头极性各测1次得0.1分，功率损耗物理概念正确得0.2分，计算值正确，误差在±0.001W范围内再得0.1分.

4 结束语

本次亚赛的实验考题总体风格与前几届相同，都是让考生按给定的方法完成任务.本次实验注重对基本实验素养的考察，如误差的计算、作图中的各种细节；注重对基本物理实验技能的考察，如第1题中通过物理量的测量推导函数关系；注重考察物理概念和物理图像的理解，如第2题中等效阻抗、反射阻抗以及损耗功率的计算等问题.与12届以色列亚赛实验题目相比，难度有所减小，但题量增加不少.特别是第2题需要进行多次的电压测量，这导致时间严重不够，学生最多只能做到第2题的第3部分.这就要求学生除了具有扎实的实验素养和实验技能外，还要求具有较快的解题速度.中国学生在此次比赛中也出现了一些本可以避免的问题导致失分，如第1题中改变角度的测量和第2题中改变可变电阻RL的测量，不少同学测量数据点个数偏少；第2题中测量线圈的电阻和电感中，R′没有仔细调节使得V和VR′差值足够小，等等.然而总体来说，本次亚赛中国学生了体现扎实的基本功和较高的实验素养，临场发挥出色，取得了近几年来在亚赛赛场上的最好成绩.

本次竞赛中要求用包含因子为2的扩展不确定度来作不确定度的估计，我们认为不必要.其实，只要给出了标准差，任何置信度下的不确定度都可以通过由标准差乘以相应的包含因子得到.其次，在第2题中计算用万用电表测量电压的不确定度时，除了万用表说明书给出的系统误差外，出题者还要求考虑万用表电压挡分辨率带来的误差，即最小分度引起的误差（最小分度的半值）.万用表说明书给出的系统误差ΔV＝±（1.0%×读数＋4个字）已经包含了某一挡末位的误差（4个字），此时再另外考虑电压挡0.5个字的分辨率误差显然没有必要.

[1] 吕斯骅，段家忯.新编基础物理实验[J].北京：高等教育出版社，2006.

[2] 马秀芳，沈元华.第八届亚洲物理奥林匹克竞赛中实验考题的分析[J].物理实验，2007，27（12）：29－33.

[3] 廖慧敏，荀坤，陈晓林.第12届亚洲物理奥林匹克竞赛试题介绍与解答[J].物理实验，2011，31（10）：16－25.

[4] 荀坤，王若鹏，陈晓林，等.第41届国际物理奥林匹克竞赛试题介绍与解答[J].物理实验，2010，30（11）：26：33.

[5] 荀坤，张朝晖，刘树新，等.第42届国际物理奥林匹克竞赛试题介绍与解答[J].物理实验，2012，32（4）：19：23.