时变采样周期网络控制系统混合H2／H∞动态输出反馈控制

樊金荣

（华中科技大学控制科学与工程学院，湖北武汉，430074）

在网络化系统（NCS）的研究中，大多数假定传感器采样间隔为已知定常数。实际上，网络带宽资源有限，负载变化、器件故障及外部干扰等因素会导致采样周期在一定范围内波动［1－2］。时变采样周期NCS的建模有三种方式：①连续系统方法：当采样周期比较小时，把系统建模成一个带有时变输入时延的连续系统模型［3－4］；②混合系统方法：将系统建模成有限脉冲系统［5－6］。文献［7］认为，这两种方法对时延大于采样周期不能普遍适用；③离散系统方法：它可分为离散切换系统［8－10］和带范数有界不确定性系统［11－12］。前者假定采样周期在已知集合内按某种规律（或随机）取值，显然有限个随机值不能完全表示采样周期的连续波动；后者选取采样周期的标称值，将采样周期的不确定性部分转化为范数有界不确定性系统结构参数。然而在该处理过程中，通常假定时延为常数或忽略时延。目前，在时变采样周期控制器设计方面基本上是状态反馈控制器，有关满足混合H2／H∞性能指标动态输出控制方面的研究少见报道。为此，本文采用矩阵Jordan分解变换方法，将具有时变采样周期和时延的NCS建模为离散时间凸多面体不确定系统，以线性矩阵不等式的形式，给出满足混合鲁棒H2／H∞性能的动态输出反馈控制器存在的充分条件和具体参数表达式，从而获得系统动态性能和稳定性两方面的平衡，数值仿真结果表明所设计的控制器能够保持系统渐近稳定。

1 NCS数学模型

考虑如下连续线性系统：

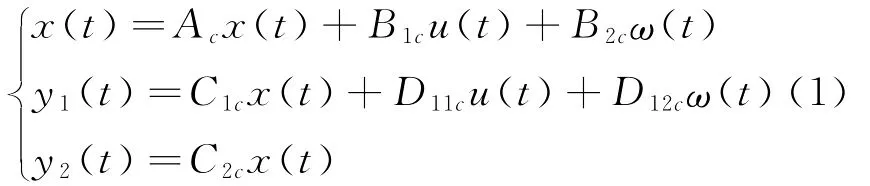
在继续讨论之前，先作如下合理假设：①网络控制系统中传感器时钟驱动，两个连续采样时刻的间隔定义为采样周期，即采样周期和时延时变、未知但有界，即这里仅考虑短时延的情形，其中数据没有丢包发生，所有的数据都能到达执行器。

基于上述假设，对系统（1）进行离散化，得到：

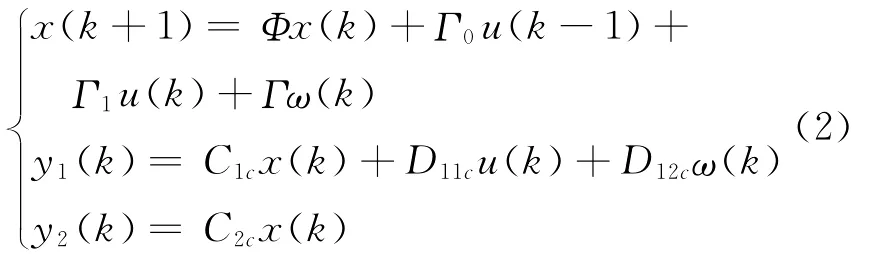
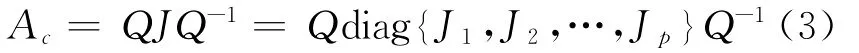
其中：Ji，i＝1，2，…，p称为Jordan块，对于互异实特征值互异共轭复根0），相应的Jordan块的指数函数可分别写为

参数k描述Jordan小块的维数（大小），Ti为模式矩阵，

使用Jordan分解和式（4）描述的Jordan块，对实数和复数特征根，相应的矩阵指数函数eAct可分别写为

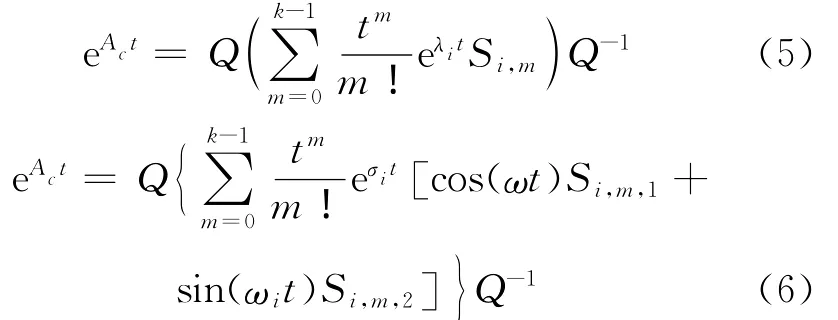
Si，m为一个与相对应的矩阵，在元素出现的地方置1，其他元素全部为0；的定义与此类似。由于指数函数的定积分仍是指数形式，可以把式（2）中包含变量可得到：

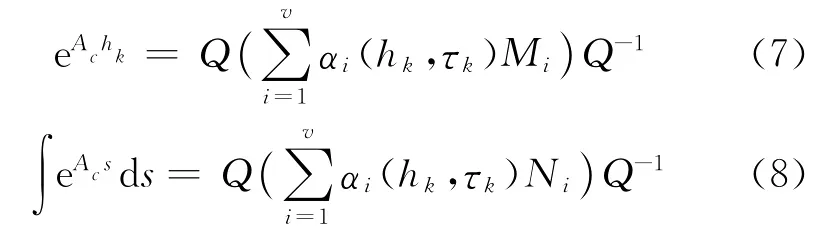
其中：v为系统矩阵Ac的最小多项式次数。对应的时变函数ai（t）（i＝1，2，…，v）在特征根为非零实数λi∈ℝ时，可写为tmeλit的形式。若特征根为0，则写为αi（t）可用Kronecker符号函数δ1，l描述，l＝1，取为1，其他为0。若特征根为共轭复数λi＝σi＋jωi，αi（t）可写为tmeσitcos（ωit）和tmeσitsin（ωit）。这里有两个变量hk和τk，t分别被取代为tahk和tahk－τk。则时变函数αi（t）的数量为ζ＝2v。Mi和Ni可通过式（5）和式（6）计算得到，是确定的矩阵。

若采样周期和时延有界，则ai（hk，τk），i＝1，2，…，ζ，也是有界的，其最小值和最大值可通过下式计算得到：

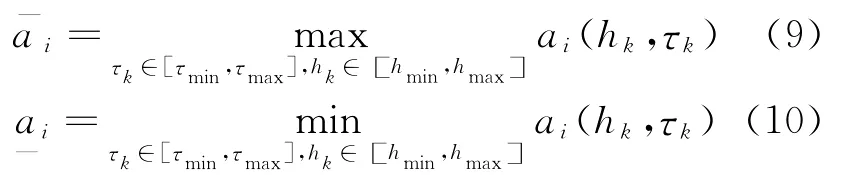
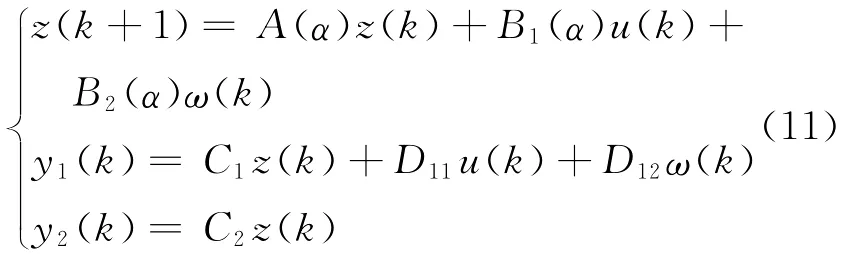
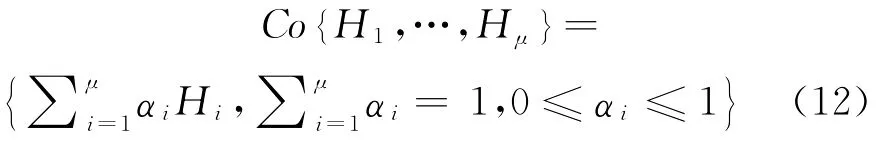
至此，将网络控制系统中的时变采样周期和时延建模成凸多面体描述的离散时间不确定系统，这是本文分析与设计的基础。

2 问题描述和预备知识

所设计的全阶动态输出反馈控制器为

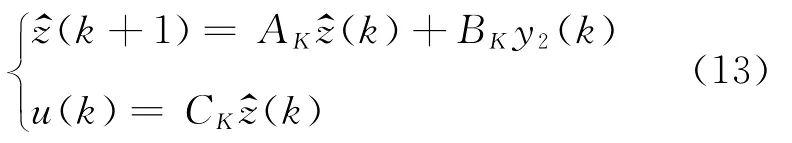
其中：z＾（k）为控制器的状态，AK、BK、CK为待确定参数。在其作用下，相应的闭环系统为

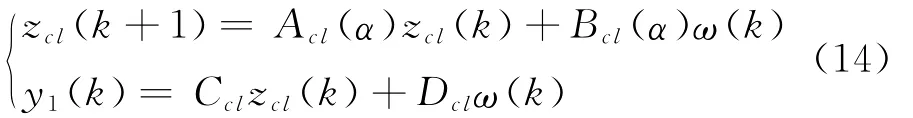
混合鲁棒H2／H∞控制问题的任务是，对于离散凸多面体不确定系统（11），要求设计的动态输出反馈控制器（13），使得对于所有允许的采样周期和时延的不确定性，闭环系统（14）渐近稳定，同时满足如下性能指标：

（1）鲁棒H2性能：最小化η，使得ω（k）到y2（k）的闭环传递函数其H2范数最小，

（2）鲁棒H∞性能：给定γ＞0，即ω（k）到y1（k）的闭环传递函数其H∞范数满足

为了解决混合鲁棒H2／H∞控制器设计问题，需要如下引理。

引理1［13］以下结论是等价的：

（1）存在对称正定矩阵P＞0，使得：

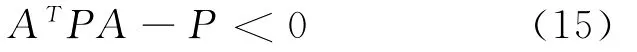
（2）存在对称正定矩阵P＞0和一般矩阵G，使得：

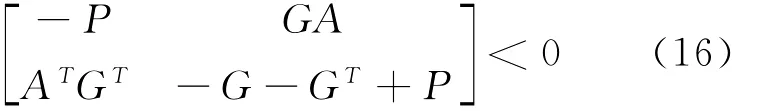
引理2［14］对于给定的η＞0，闭环系统（14）渐近稳定，且其充要条件为存在实对称正定矩阵对所有的时变参数，且满足：

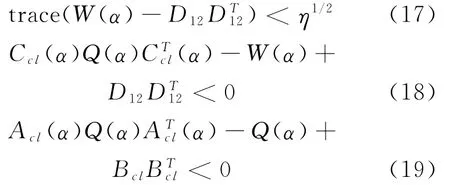
3 主要结果

由于参数α∈L的不确定性，对称正定矩阵Q（α）未知。式（18）和式（19）中，存在着未知矩阵变量Q（α）和系统矩阵Acl（α），Ccl（α）的耦合非线性性项和Acl（α）Q（α）需要引入一个自由变量，从而将其解耦，使之变成线性矩阵不等式的形式。

下面的定理给出与引理2等价且具有参数依赖Lyapunov函数的H2性能准则。

定理1 对于给定的η＞0，闭环系统（14）渐近稳定，且其充要条件为存在实对称正定矩阵和一般矩阵G，对所有的时变参数α∈L，且满足H2：

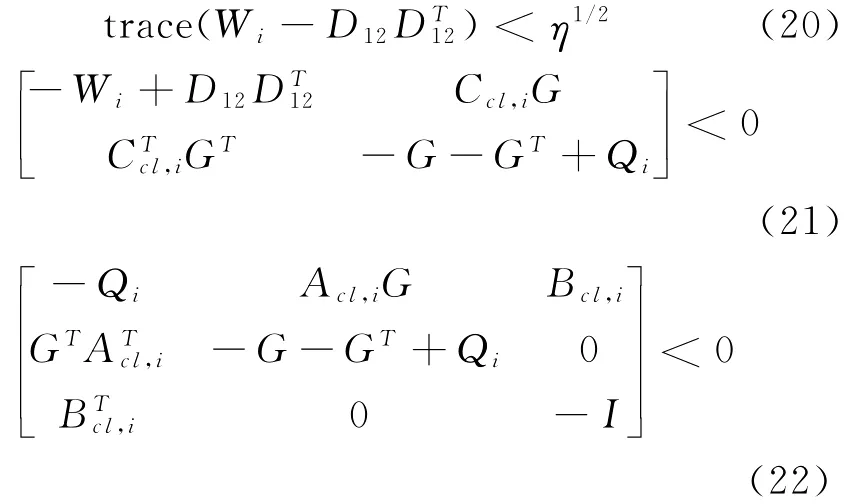
证明：式（20）左边乘αi后求和，可以直接得到式（17），式（21）和式（22）左右同乘αi后求和，运用矩阵Schur补定理和引理1，可以直接得到式（18）和式（19）。证毕。

由离散时间系统的有界实定理［15］，可得到Lyapunov函数矩阵Pi与闭环系统矩阵Acl，i解耦的H∞性能准则。

定理2 给定常数γ＞0，若存在实对称正定矩阵Pi，i＝1，2，…，μ，对所有的时变参数有和一般矩阵G，满足：

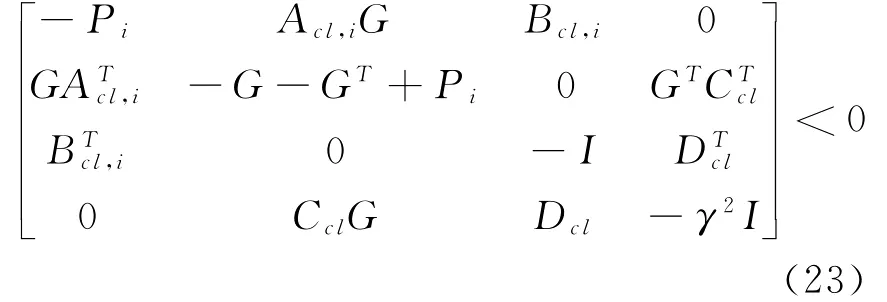
则闭环系统（14）渐近稳定且满足H∞性能指标。

证明：过程同定理1，同样要用到引理1和Schur补定理，其过程略。

需要说明的是，在式（20）～式（22）中，若令W＝Wi，Q＝Qi，Γ＝Γi，得到参数不依赖的Lypaunov函数，对应的H2性能称为参数不依赖H2性能准则。与之相对应，在式（23）中，若令P＝Pi，则得到的H∞性能也相应地称为参数不依赖H∞性能准则，其结果具有保守性。

定理1和定理2分别给出了时变采样间隔和时变时延网络控制系统H2、H∞性能的条件。如果上面两个定理同时成立，那么闭环系统（14）就同时具有混合H2／H∞性能。若令Qi＝Pi，式（23）包含式（22）的条件，因此就有如下定理。

定理3 给定常数γ＞0，若存在实对称正定矩阵一般矩阵Z、H和适ii当维数矩阵2，…，μ，若以下凸优化问题

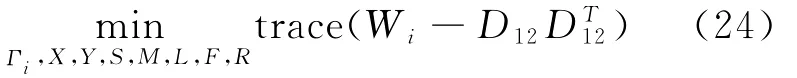
约束于：

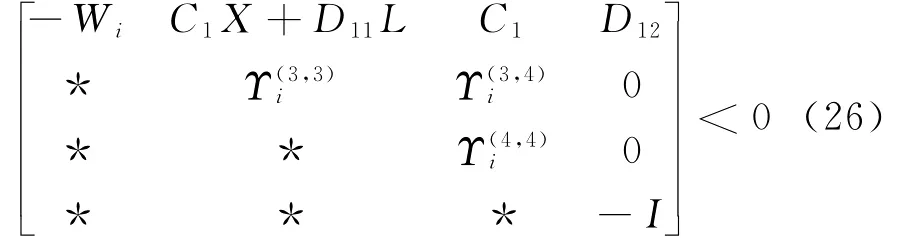
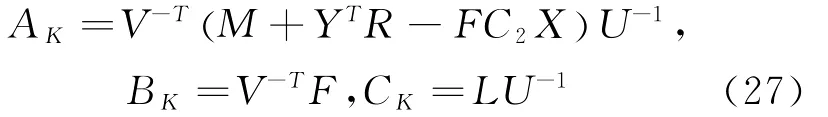
证明：由式（22）和式（23）可知G非奇异，G－1存在，取不失一般性，假定X＞0、Y＞0、U和V分别行满秩、列满秩。定义变化矩阵这样有：在式（23）两边左右乘diag及其转置，进行合同变换。并令得到：

对H2性能指标，运用相同的证明过程，对式（21）两边同乘及其转置，进行合同变换，很容易得到式（26）。在式（25）和式（26）中，有暗含着：

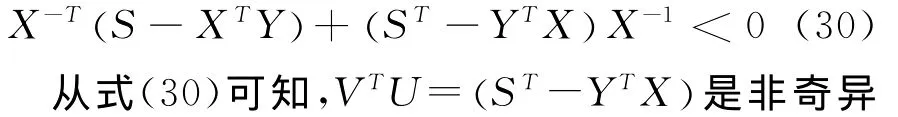
的，即V和U是非奇异的。优化问题式（24）是一个具有线性矩阵不等式（LMI）约束和线性目标函数的凸优化问题，因此可以应用LMI工具箱中的mincx求解器来求解，得出X、Y、S、M、L、F和R值。若U和V可调用Matlab函数［V1，U1］＝则有将上述参数代入式（27），得到动态输出反馈控制器的参数。证毕。

值得注意的是，在式（24）～式（26）中，令W＝Wi，Γ＝Γi，得到参数不依赖的Lypaunov函数，对应的H2／H∞性能称为参数不依赖H2／H∞性能准则（二次稳定准则）。约束条件更强（变量参数少），得到的性能具有保守性。

4 仿真实例

这里引用文献［8］中的例子，连续时间系统如下：

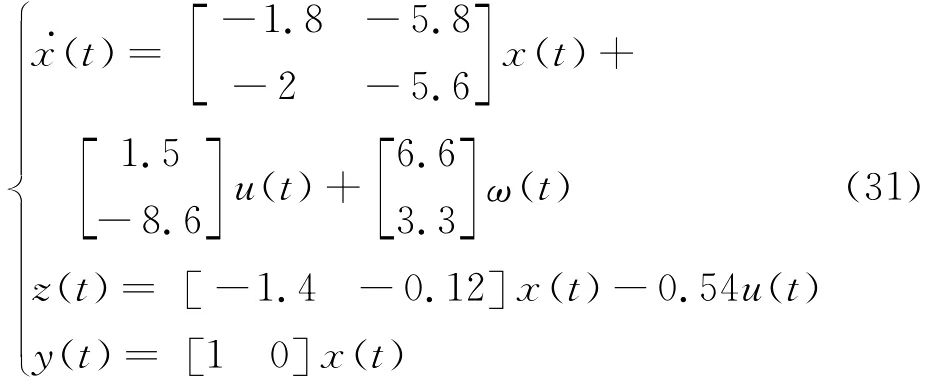
在文献［8］中，系统采样周期hk在集合中切换，对应的时延上限为显然时延也随采样周期切换而变化。在这里，我们设定采样周期和时延连续变化，未知有界，即0，0.1［］s，这样更具有普遍性。连续系统矩阵Ac的特征根为λ1＝0.2，λ2＝－7.6，连续时间系统是不稳定的。

（1）首先考虑鲁棒H2、H∞性能，由定理1和定理2分别得到ηmin＝4.717 1，γmin＝12.136 74。

（2）考虑混合H2／H∞性能指标，即寻找优化问题式（24）约束于式（25）和式（26），分别用参数依赖和参数不依赖的Lyapunov函数取不同的γ＞0值，得到不同H2性能指标ηmin。图1给出在混合H2／H∞鲁棒控制器作用下相应闭环系统的实际鲁棒H2性能与鲁棒H∞之间的关系。若取γ＝12.136 74，优化问题式（24）无解。由此可看出，H2性能指标ηmin随抑制扰动γ增加而减小，说明系统鲁棒性与其动态性能之间存在矛盾，提高系统鲁棒性是以降低其动态性能为条件，反之依然。同时也说明，采用二次Lyapunov函数得到的控制器具有很强的保守性。

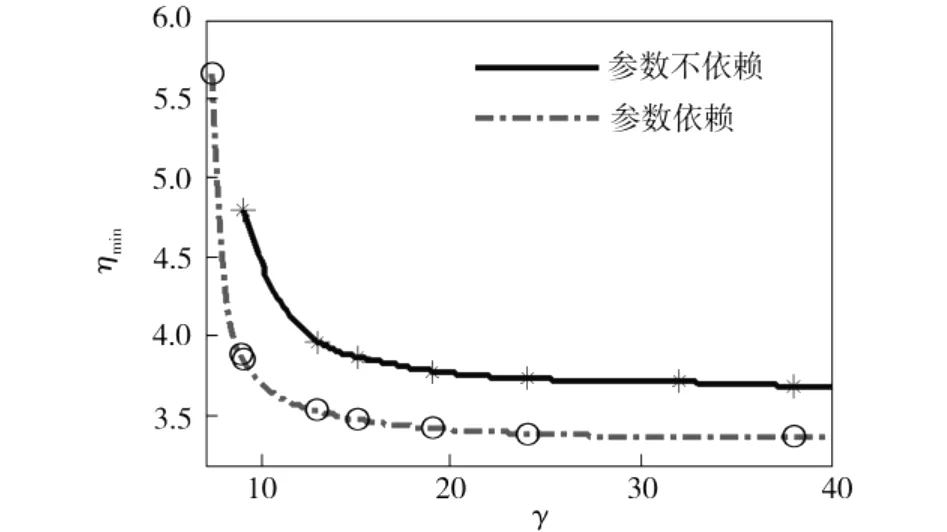
图1 H2性能指标与抑制扰动γ之间的关系Fig.1 Relationship between H2 andγ

设外部干扰信号ω（k）取值，其中n（k）表示零均值，协方差为0.1的正态分布噪声。即：

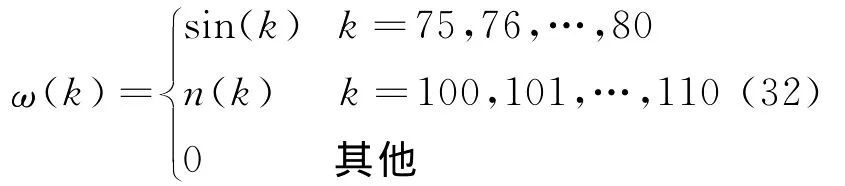
假设在第一个控制信号到达被控对象之前，控制信号u（k）＝0（k＜0），对应的离散时间系统中，初始状态z（0）＝［1－1 0］T，取γ＝17时，求解优化问题式（24）。选用参数依赖的Lypaunov函数方法，即在式（24）中，取不同的Wi，在约束式（25）和式（26）中，取不同的Γi，i＝1，2，…，μ，得到参数依赖混合棒H2／H∞动态反应器如下：

图2为时变采样周期和时变时延NCS系统在有外界干扰情形下的闭环系统状态响应。由图2可看出，对不稳定的连续系统，所设计的动态输出反馈控制器能使系统保持渐近稳定，同时对外界干扰具有很好的抑制性。

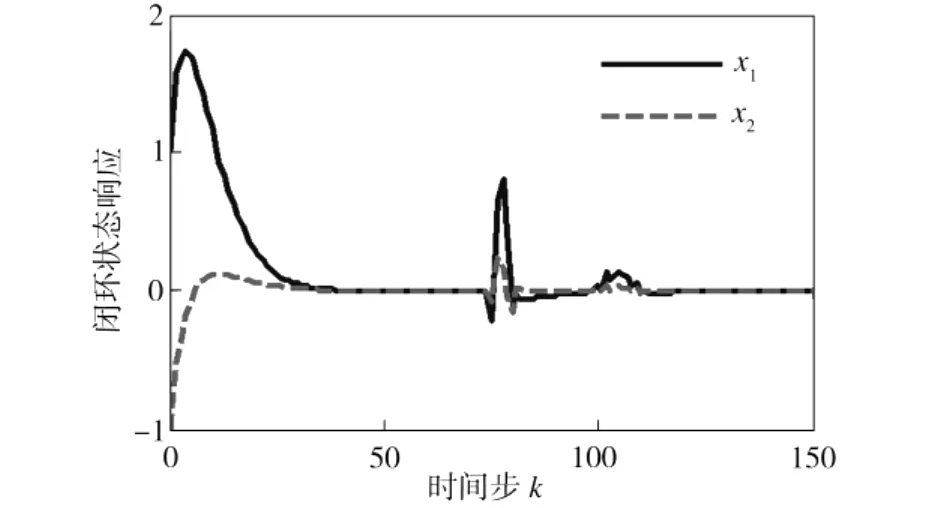
图2 闭环系统状态响应Fig.2 Response of the closed－loop systeM State

5 结语

本文将时变采样周期和时延的NCS建模为离散时间凸多面体不确定模型。以线性矩阵不等式的方式给出满足混合H2／H∞性能的动态输出反馈控制器可解条件及求解算法。数值仿真验证了所提出设计方法的有效性。本文在离散时间系统框架下进行动态输出反馈控制设计，为时变采样周期的NCS研究开辟了新的途径。

［1］ W P M H Heemels，D W N Van，M C F Gielen.Comparison of overapproximation methods for stability analysis of networked control systems［C］∥Proc of the 13th International Conf on Hybrid Systems on Computation ＆Control，Stockholm，Sweden，2010：181－190.

［2］ E Fridman.Arefined input delay approach to sampled－data control［J］.Automatica，2010，46（2）：421－427.

［3］ H Fujioka.Stability analysis of systems with aperiodic sample－and－hold devices［J］.Automatica，2009，45（3）：771－775.

［4］ E Fridman，A Seuret，J P Richard.Robust sampled－data stabilization of linear systems：an input delay approach［J］.Automatica，2 0 0 4，4 0（8）：1 441－1 446.

［5］ P Naghshtabrizi，J P Hespanha，A R Teel.Exponential stability of impulsive systems with application to uncertain sampled－data systems［J］.Systems＆Control Letters，2008，57：378－385.

［6］ P Naghshtabrizi，J P Hespanha，A R Teel.Stability of networked control systems with variable sampling and delay［J］.Transactions of the Institute of Measurement and Control，2010，32（5）：511－528.

［7］ Y S Suh.Stability and stabilization of nonuniforMSampling systems［J］.Automatica，2008，44（12）：3 222－3 226.

［8］ 王玉龙，杨光红.具有时变采样周期的网络控制系统的H∞控制［J］.信息与控制，2007，36（3）：278－284.

［9］ R A Borges，R C L F Oliverira，C T Abdallah，et al.RobustH∞networked control for systems with uncertain sampling rates［J］.IET Control Theory Appl，2010，4（1）：50－60.

［10］L Montestruque，P Antsaklis.Stability of modelbased networked control systems with time－varying transmission times［J］.IEEE Transactions on Automatic Control，2004，49（9）：1 562－1 572.

［11］薛燕，刘克.变采样网络控制系统的鲁棒控制［J］.计算机工程与应用，2008，44（27）：240－244.

［12］I Michal，G Daniel，L Steven.Stabilization of systems with variable and uncertain sampling period and time delay［J］.Nonlinear Analysis：Hybrid Systems，2010，4（2）：291－305.

［13］M C Oliverira，J Bernussou，J C Geromel.A new discrete－time robust stability condition［J］.Systems and Control Letters，1999，37（4）：261－265.

［14］俞立.鲁棒控制－线性矩阵不等式处理方法［M］.北京：清华大学出版社，2002：34－40.

［15］Xu Shengyuan，Lam James，Zou Yun.New versions of bounded real Lemmas for continuous and discrete uncertain systems［J］.Circuits Syst Signal Process，2007，26（6）：829－838.