非对称混合梁独塔斜拉桥风致颤振分析

杨从娟

(石家庄铁道大学工程力学系,石家庄 050043)

1 概述

斜拉桥是典型的柔性结构,在风力作用下极容易发生振动和变形。斜拉桥的气动弹性颤振问题是该桥型急需更深入研究的课题。斜拉桥的风致颤振是斜拉桥在施工的不同阶段和成桥阶段空气流动场和桥跨结构相互作用,桥跨结构从气流中获得能量,引起结构振动的能量大于结构阻尼所耗散的能量时,会产生桥梁结构发散振动的气动弹性失稳现象[1-7]。

斜拉桥抗风设计中,风致颤振已成为控制设计关键要素。研究不同结构的斜拉桥的风致颤振问题具有较深的应用价值。

2 工程情况

新建海河大桥位于天津新港船闸北岸,是典型的非对称双索面独塔斜拉桥,主桥孔径布置310 m+2×50 m+2×40 m；主梁在主孔采用钢与混凝土混合型钢箱梁,长300 m；主桥其余主梁均为预应力混凝土箱梁结构,梁高3 m,桥面宽23.17 m；独塔采用“钻石型主塔”,塔高165.8 m。此桥桥址位于海河入海口处,季节性风力明显；桥址历年平均风速4.5 m/s；最大风速24 m/s；基本风压412 Pa,频率1.2%,10 min平均最大风速为22 m/s。

截止现在,该桥完成了主塔的施工,预应力箱梁部分的主梁已采用支架现浇完成,为保证主塔和主梁施工过程的安全性和运营阶段的安全性,有必要进行抗风分析。

3 新建海河大桥风致颤振分析

3.1 计算模型的建立

利用Midas有限元软件,考虑各种墩塔梁等结构的刚度、质量和不同结构间的边界条件,建立有效的三维空间模型,如图1所示。其中,主墩、主塔、锚固墩等桥墩采用梁单元模拟,斜拉索采用索单元模拟；扁平流线形钢箱梁和预应力混凝土箱梁也采用梁单元模拟,其截面形式见图2、图3。全桥共1 004节点；梁单元876个,索单元78个,共计954个单元。

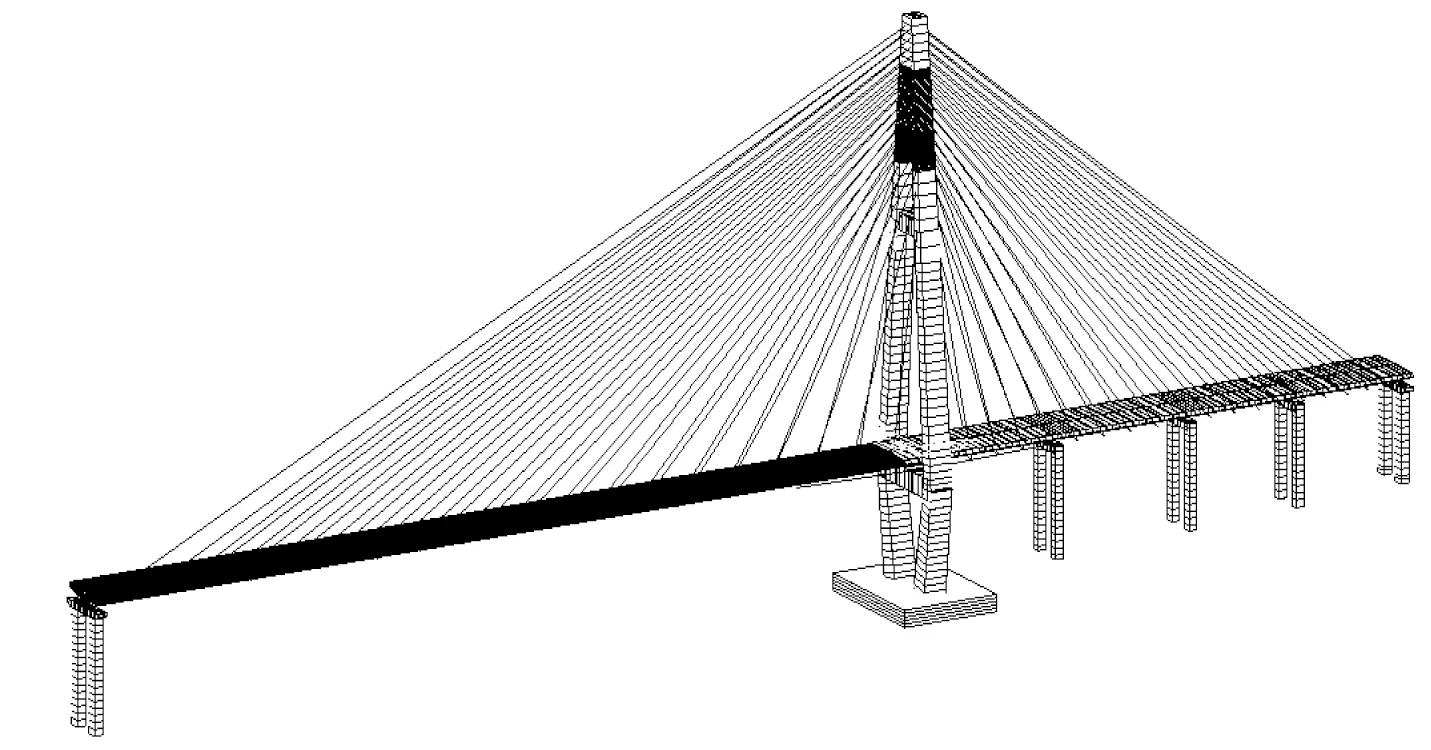
图1 空间计算模型

图2 扁平流线形钢箱梁截面

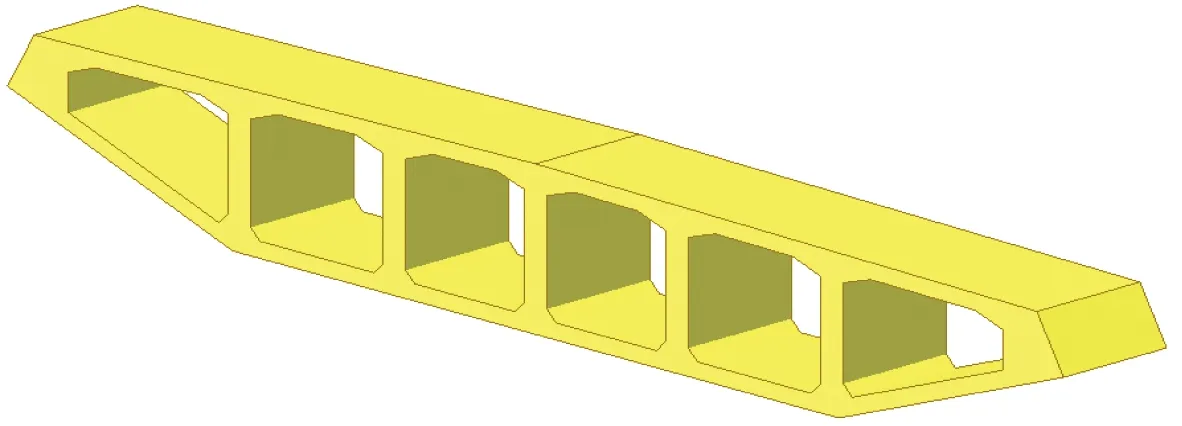
图3 混凝土箱梁截面

3.2 2种状态动力特性计算分析

本桥的施工采用先主塔施工,后预应力混凝土箱梁支架现浇,然后是扁平流线形钢箱梁分节吊装安装。根据该桥的施工过程,桥梁结构动力分析,按钢箱梁主梁最大单悬臂和成桥运营2种工况进行自振特性分析,考虑振型的贡献每种工况采用子空间迭代法求出前50阶振型,图4表示施工中钢箱梁最大单悬臂状态第1振型图(频率为0.198 Hz),图5表示成桥状态第1振型图(频率为0.213 Hz)。由于篇幅有限,仅列出2种状态下前10阶动力特性值，见表1、表2。

根据振型特征和周期分析,可以得出新建海河斜拉桥的动力特性为：

(1)成桥状态基本周期为4.7 s,第1振型为纵飘,属较长周期结构,符合半漂浮体系斜拉桥的特征；

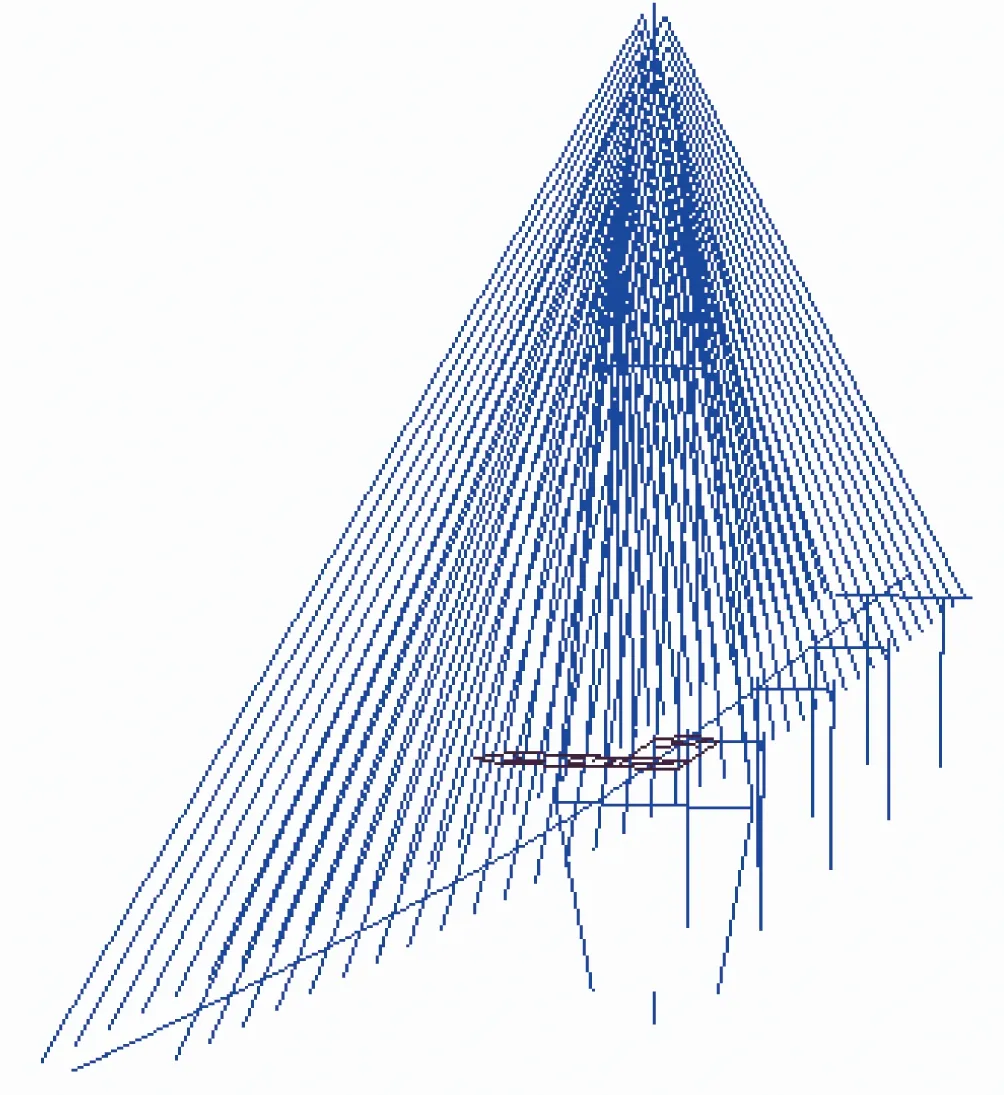
图4 最大单悬臂状态第1振型(频率0.198 Hz)

图5 成桥状态第1振型(频率0.213 Hz)

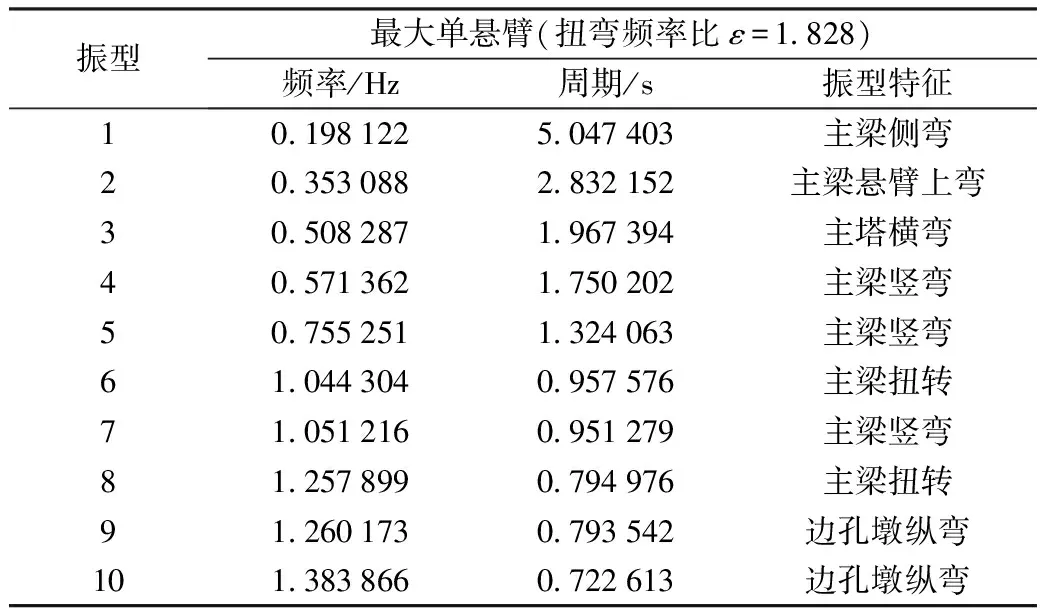
表1 最大单悬臂动力特性值

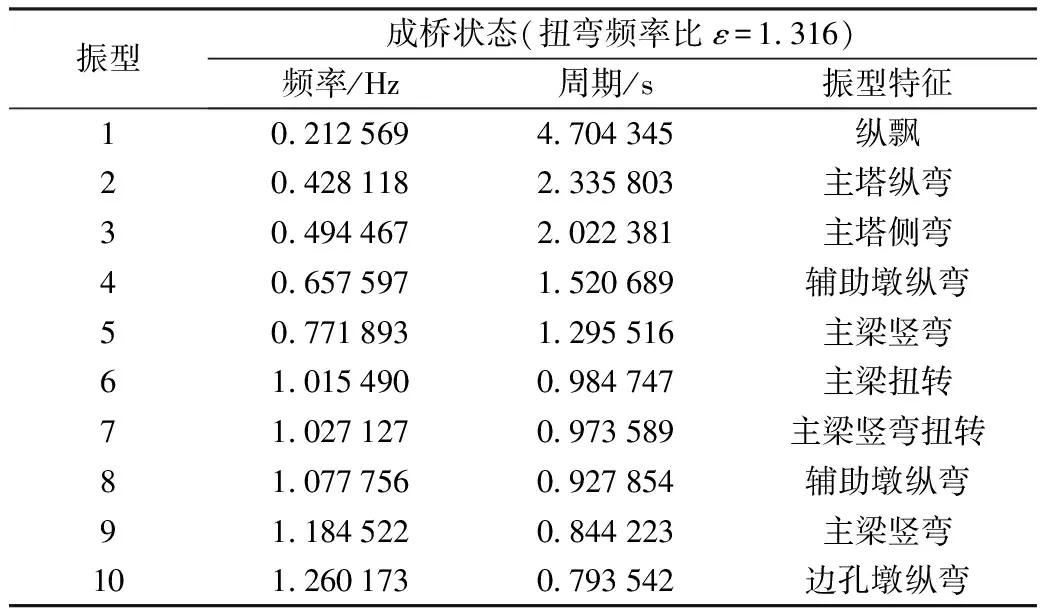
表2 成桥状态的动力特性值

(2)长周期对斜拉桥抗风稳定有利,但会引起主梁的纵向漂移位移过大,因此设计中索塔横梁上设置2组纵向阻尼器,以防主梁纵向位移过大。

3.3 颤振临界风速的评估

通过上述单悬臂状态和成桥状态的振动特性分析,2种状态下的主梁竖弯基频低于扭转基频,也就是说,弯扭耦合颤振临界风速低于纯扭转颤振的临界风速,因此,弯扭颤振临界风速大于检验风速,就不必计算纯扭转颤振的临界风速。

弯扭耦合颤振临界风速采用下列公式计算[8-9]

式中,μ为桥梁与空气的密度比；ηa为攻角效应系数；ηs为主梁断面形状影响系数；ωh为基阶竖弯自振圆频率；ε为扭弯频率比；r为惯性半径；b为半桥宽。

分离流耦合颤振临界风速由下列公式确定[8-9]

在最大单悬臂和成桥状态下弯扭耦合颤振临界风速和分离流耦合颤振临界风速的计算结果见表3。

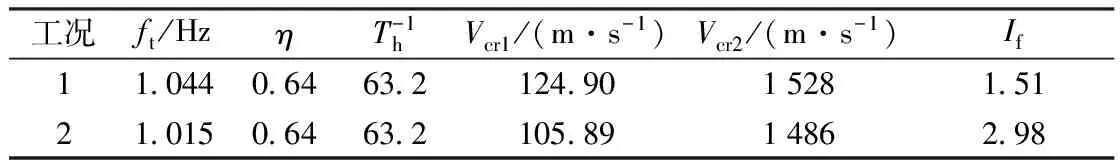
表3 2种工况状态下的计算结果

注：η=ηsηa；If=[Vcr]/(ftB)

成桥运营状态,主梁设计基准风速[10]

Vd=Vs10(Z/10)α=46.87 m/s；

成桥颤振检验风速

[Vcr]=1.2μfVd=70.25 m/s；

施工阶段颤振检验风速

[Vcr]=ηVd=36.56 m/s。

根据表3,从2种状态下的临界风速和检验风速对比看,分离流耦合颤振临界风速远大于相应状态颤振检验风速；颤振检验风速36.56 m/s远小于处于最大单悬臂状态主梁弯扭颤振临界风速为124.90 m/s,；颤振检验风速70.25 m/s小于成桥状态主梁弯扭颤振临界风速为105.89 m/s。

通过上述分析,该斜拉桥在当地最大风速下不会发生颤振失稳。

由表3可知：该桥最大单悬臂施工阶段颤振稳定性指数If小于2.5；成桥状态稳定性指数If大于2.5小于4.0[10]。

4 结论

(1)通过分析,新建海河大桥最大单悬臂施工阶段和成桥状态,主梁自激风振的检验风速均小于颤振临界风速,因此,该桥钢箱梁悬臂拼装全过程和成桥运营状态均能抑制自激风振。

(2)成桥稳定性指数2.5

参考文献：

[1] 王冬立.结构和气动非线性机翼的颤振与控制研究[D].天津：天津大学,2005.

[2] 曹海滨.大跨度混合梁斜拉桥抗风性能分析[J].铁道标准设计,2005(10)：36-38.

[3] 张新军,陈艾荣,项海帆.大跨度桥梁的三维非线性颤振频域分析[J].同济大学学报：自然科学版,2001(1)：20-24.

[4] 葛耀君,项海帆.随机风荷载作用下的桥梁颤振可靠性分析[J].土木工程学报,2003(6)：42-46.

[5] 李朋主.大跨度桥梁颤振分析与研究[D].沈阳：东北林业大学,2006.

[6] 刘海英.具有立方非线性机翼极限环颤振的研究[D].天津：天津大学,2004.

[7] 白玉磊.FRP斜拉桥抗风性能初探[D].大连：大连理工大学,2009.

[8] 陈政清.桥梁风工程[M].北京：人民交通出版社,2005.

[9] 李国豪.桥梁结构稳定与振动[M].2版.北京：中国铁道出版社,1992.

[10] 项海帆,鲍卫刚,等.公路桥梁抗风设计规范[S].北京：人民交通出版社,2004.