“等速率追击”问题研究
2012-01-23王光宇
王光宇
(上海松江区教师进修学院附属立达中学 上海 201600 )
1 问题由来
诸多物理文献均论及这样一道竞赛题.
题目:如图1所示,有一只狐狸以不变的速率v1沿直线AB逃跑,一猎犬以不变的速率v2追击,其追击的方向始终对准狐狸,某时刻狐狸在F处,猎犬在D处,FD⊥AB,FD=L假设v2>v1,试求此时猎犬的加速度是多少?

图1
追击问题在运动学部分比较典型,此类问题综合性较强,与生活联系较为紧密.但多数问题是同一直线上的追击,相对而言容易解决.本题论及的问题较特殊,因为追赶者的速度方向不断发生变化,其追逐的轨迹为曲线.
将猎犬和狐狸抽象为质点模型,狐狸在逃逸过程中其速度保持不变做匀速直线运动,猎犬在追逐狐狸的过程中保持不变的速率,故将本问题称之为“等速率追击问题”.狐狸沿AB方向,猎犬追击狐狸且始终瞄准狐狸,其运动方向不断发生改变,加速度和速度分量随之变化,其运动轨迹应是一条曲线.
本文仅就这一过程,研究猎犬运动的轨迹曲线方程、速度分量的变化规律和加速度的变化规律等问题,笔者对这个问题作如下探讨,以供读者在教学或竞赛指导中参考.
2 问题讨论
2.1 猎犬在D点的加速度
解析:猎犬的速率不变,追击过程始终要瞄准狐狸,其速度方向不断变化,运动为变速运动.如图1所示,假设在开始的一段无限短时间Δt内,狐狸和猎犬分别到达F′,D′,过D′作D′C⊥DF′,直角△DD′C与直角△F′FD相似,对应角相等,即∠DCD′=∠FDF′=α.由于α角很小,DD′可近似看成半径为R一段圆弧.
猎犬的速度方向转过的角度
(1)
狐狸奔跑的距离为
v1Δt=αL
(2)
由式(1)、(2)可得猎犬在D点的加速度
(3)
2.2 猎犬追上狐狸所需时间
解析:如图2(a)所示,猎犬追击狐狸的某一时刻,猎犬到达D′点,狐狸到达F′点,沿D′F′方向两者相互接近的速度为
Δv=v2-v1cosθi
(4)
由式(4)得Δt时间内相对缩短的距离
Δli=(v2-v1cosθi)Δt
(5)

图2
由式(5)累加得
即
(6)
沿x轴方向上相互接近的距离为
Δlix=(v2cosθi-v1)Δt
(7)
猎犬追上狐狸,即它们相互接近的距离为零.由式(7)得
(8)
由式(6)、(8)联立可得
(9)
2.3 猎犬追击狐狸的运动轨迹

图3
解析:如图3所示,以F点为坐标原点,FD为x轴正方向、FB为y轴正方向建立平面直角坐标系,假设经过时间t,猎犬到达坐标系中的D′点(x,y),由于猎犬在追击的过程中方向始终对准狐狸,故在该时刻v2的方向应指向F′点,狐狸在该时刻的位置为F′点(0,v1t),假设猎犬运动的轨迹方程为
y=f(x)
因为D′F′为该点猎犬运动轨迹的切线,所以
即
(10)
将式(10)两边对x求导得
(11)
由ds2=dx2+dy2得
(12)
由式(12)得
(13)
将式(13)代入式(11)得
(14)
令
则
式(14)可化为
(15)
微分方程(15)的初始条件
解微分方程式(15)得
(16)
由式 (16)得
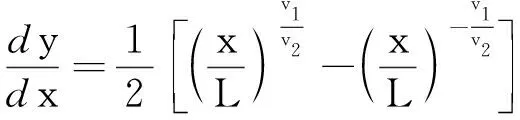
(17)
微分方程(17)的初始条件为y(L)=0,解方程可得
(18)
猎犬到达D′(x,y)通过的路程
(19)
由式(17)、(19)得
(20)

2.4 猎犬追击狐狸速度分量的变化
解析:式(20)两边对x求导得
(21)
由式(21)得
(22)
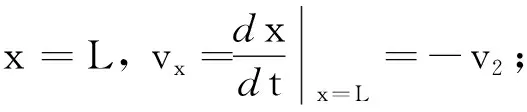
由式(17)、(22)得
(23)
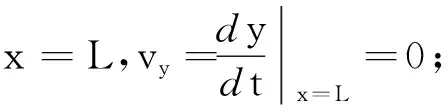
2.5 猎犬追击狐狸加速度的变化
解析:由式(17)得
(24)
(25)
由式(25)得
(26)

为方便起见,本文取v2= 20 m/s,v1=10 m/s,L=100 m ,使用Excel绘图工具绘制式(18)、(26)的函数曲线,图像如图4所示.

图4
从图像可见:x=0;y=0为其轨迹的两条切线;猎犬两速度分量严格单调变化;加速度大小先增加后减小,中间出现一个极大值,极值点对应的位置猎犬所受到的摩擦力最大,也是猎犬追击过程中最易打滑“摔跤”的地方.
3 结语
通过对“等速率追击”问题的研究,系统地呈现了猎犬追击狐狸过程中物理量的变化规律,其问题的解析体现了研究物理问题的诸多方法,比如模型法、近似处理法、微元法和微分方程法等.若在教学中针对某一问题能采用多种方法进行逐层深入的探讨与分析,对拓宽学生的知识视野大有裨益.
参考文献
1 程稼夫.中学奥林匹克竞赛物理教程·力学篇.合肥:中国科技大学出版社,2004
2 漆安慎,杜婵英.普通物理学教程·力学(第二版).北京:高等教育出版社,2004
3 四川大学数学系高等数学教研室.高等数学(第二册).北京:高等教育出版社,1995
