修正Terzaghi理论在吹填土固结计算中的应用

郭帅杰，王保田，张福海

(河海大学 a. 岩土力学与堤坝工程教育部重点实验室，b. 岩土工程科学研究所， 江苏 南京 210098)

Terzaghi一维固结理论自提出以来在土体固结沉降计算中得到广泛应用，具有简单实用的优点，经受了大量工程实践检验，在此基础上发展出适于吹填土固结的各种修正方法扩展Terzaghi理论的应用范围[1]。但Terzaghi理论主要应用于大范围线弹性小变形饱和土体固结计算，对压缩性大、孔隙比高的吹填土体固结问题存在理论应用上的局限[2]，计算结果与土体实际沉降相差甚远。Gibson[3]等采用流动坐标代替空间坐标避免土体沉降引起的坐标误差建立大变形固结方程，在吹填土、淤积土、河、海相新沉积粘土等软土体大变形固结计算中得到广泛应用。

Terzaghi理论方程建立过程中并没有小变形约束，仅在利用边界条件求解固结方程解析解时采用小变形假定，小变形固结方程是Gibson大变形固结方程某些假定情况下的简化处理[4]。Terzaghi理论在固结方程建立流程上不存在小变形限制，那么通过有限应变理论与固结参数固结过程中的连续修正方法将经典固结理论推广到软土地基的大变形固结沉降计算是可行的。

Mikasa和Gibson[5]作为一维大变形固结理论的主要开拓者，都致力于将Terzaghi小变形理论推广到更普遍的大变形固结理论。谢新宇[6]等对大变形固结系数进行研究，得到不同情况下固结系数的变化趋势。Duncan[7]的研究指出假定固结系数在固结过程中恒定是不合理的，土体在固结过程中表现出非线性非弹性特点。因而，应用非线性土体本构方程表征固结参数的变化趋势，以及在固结沉降计算中的具体应用是值得深入研究的内容。

Terzaghi固结方程求解的关键是固结系数固结过程中的常数性假定。土体固结系数与渗透性、压缩性相关，而渗透性、压缩性随土体固结过程连续变化可分别表达为孔隙比的非线性函数，固结系数也不为常数，随固结过程不断变化，将固结系数表达为孔隙比表达式更能反映吹填土固结系数在固结过程中变化规律[8]。Terzaghi固结方程解析解应满足小变形假定，将大变形沉降应用有限应变理论分段表达，满足小变形条件(1%～5%)，逐级叠加求解各步长沉降量，得到固结沉降曲线。

1 Terzaghi固结方程

Terzaghi理论以超孔压为控制变量，根据边界条件与初始超孔压分布求解固结方程。为便于控制应变步长与时间步长，以孔隙比作为方程变量，根据边界条件与初始条件获得方程解析解。

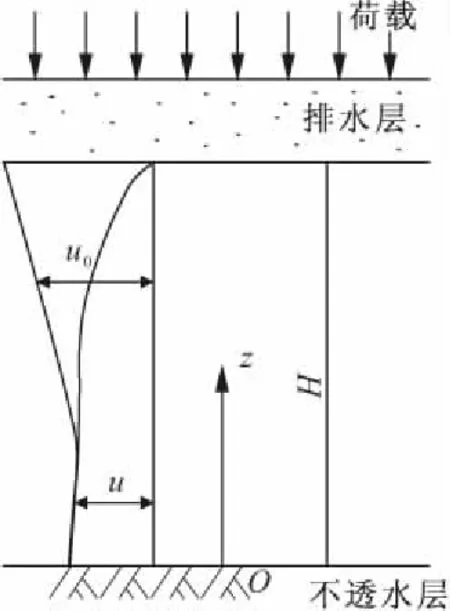
图1 土层单向固结示意图

1.1 超孔隙水应力固结方程及解析解

图1所示固结土层场地条件下，土层坐标零点位于底部不可压缩层，方向竖直向上，排水上边界，下边界不透水，初始超孔压分布为u0，静孔压分布为u。超孔压控制变量固结方程为

(1)

式中，u为超静孔隙水应力；cv为固结系数；t为固结时间维度；z为固结土层空间坐标。

(2)

式中，Ω为排水边界；Γ为不透水边界。

应用分离变量法，(1)式在(2)式条件下解析解为

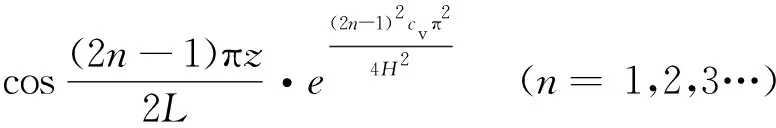
(3)

1.2 孔隙比固结方程及解析解

图1中土层固结示意图中边界条件下，孔隙比控制变量固结沉降归结为(4)式固结问题。

(4)

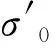
应用分离变量法，方程(4)式解析解为

(5)

式中，n为自然常数(n=1,2,…)。式(5)可得单面排水情况下任一点、任意时刻相对初始状态沉降量S(z,t)与平均应变固结度Ut

(6)

式中，St，S∞为固结历时t后沉降量和稳定沉降量。

2 修正Terzaghi理论

2.1 固结参数固结过程中的变异性

渗透性、压缩性作为最重要的固结参数在吹填土体固结过程连续变化，不满足Terzaghi常量假定，两固结参数在固结过程中变化趋势如图2所示，固结过程中渗透系数、压缩系数均非常数。

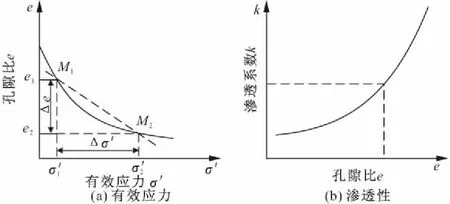
图2 土体非线性本构关系

Gibson[3,5]大变形固结方程求解时假定方程参数g(e)，λ(e)为常量，得到有效应力、渗透系数关于孔隙比的半对数表达式；方开泽[9]、洪振舜[10,11]等由淤泥渗透固结试验，测定有效应力、渗透系数与孔隙比间非线性关系，采用半对数函数关系式进行拟合；Fox[12]应用孔隙比与有效应力、渗透系数间分段线性关系代替非线性关系，形成的大变形数值模型在离心试验中得到较好应用。Lucas[13]根据室内沉降柱模拟粘性泥沙沉降试验结果采用(7)和(8)式拟幂次函数关系表达土体非线性本构关系。

σ′=Kσ(1+e)n

(7)

k=Kk(1+e)m

(8)

式中，e为孔隙比；σ′为有效应力；Kσ为有效应力参数；n为有效应力指数参数；k为渗透系数；Kk为渗透参数；m为有效应力指数参数。

2.2 固结系数

一维沉降固结系数采用土体非线性本构关系修正，在经典Terzaghi固结系数计算基础上，引入修正固结变量参数，反映大变形固结沉降中固结参数的非线性特点。固结系数cv一般定义为

(9)

将式(9)中k与mv作为固结参数变量以(7)(8)式代入，得到修正一维固结系数cv表达式

(10)

为得到cv在土体固结过程变化趋势和主要影响因素，将固结系数cv关于孔隙比e求导。

(11)

(11)式中Kk、Kσ为正值，固结系数导数正负由-n(n+m)正负性确定，可预测固结系数在固结过程中的变化趋势。根据淤积泥沙沉降柱试验结果，n=-3.40；m=7.72，cv′>0恒成立，即固结系数在固结过程中保持减小趋势[14,15]。

2.3 修正Terzaghi理论在大变形固结中应用

为修正大变形问题中经典Terzaghi固结理论的适用性问题，修正Terzaghi固结理论以土层有限应变固结理论为基础，采用分段计算方法，控制每一个沉降计算步长上的应变步长，使其满足小变形要求；计算每一应变步长上对应时间步长，经沉降累加与时间累加计算得到吹填土体时间维度上的固结曲线。根据计算得到的土体内部实时孔隙比，调整每一应变步长上固结参数，主要包括平均孔隙比、渗透系数、体积压缩系数、固结系数等固结参数调整，每一个应变步长均采用(5)、(6)式独立求解。

限定应变步长ε，由初始孔隙比分布及固结参数代入式(5)计算第i个时间步长Δti上孔隙比分布ei(z)，由式(12)计算土层平均孔隙比及应变。

(12)

εi<ε，不改变固结参数，增大时间步长Δti计算(12)式；εi≥ε，循环计算时i=i+1，T(i)=T(i-1)+Δti为固结历时；固结参数由(12)式修正。固结参数修正为

(13)

边界条件为

(14)

代入式(5)进行新应变步长计算ei+1(z)。最后一级应变步长一般达不到ε，设定时间步长限值tlimit，当Δti>tlimit时强制结束循环求解过程。

2.4 程序实现流程

根据修正Terzaghi理论计算流程，采用Matlab工具内部语言编制计算程序，通过循环调整计算得到固结计算结果。程序实现流程如图3所示。

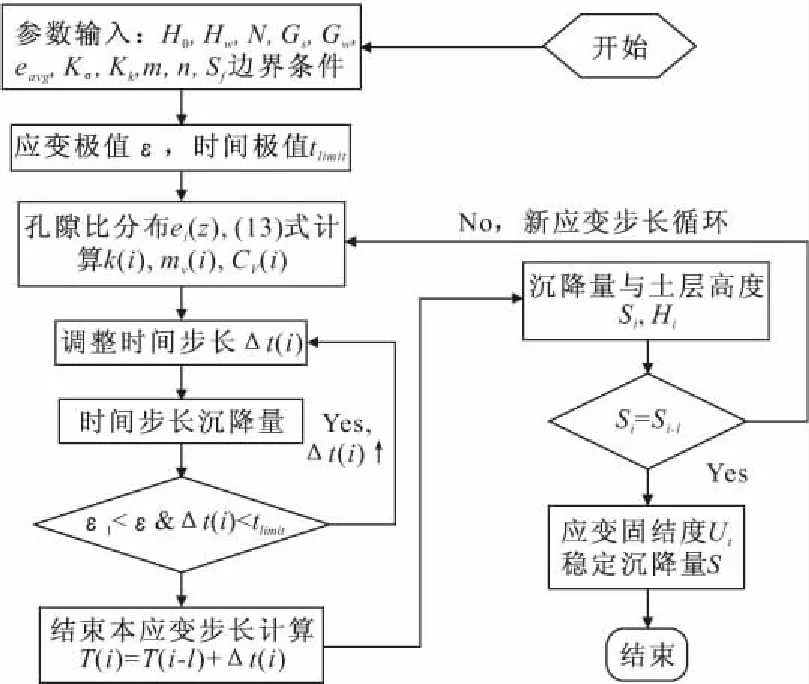
图3 修正Terzaghi方法程序实现流程

3 修正Terzaghi算例验证

应用算例从三个方面对修正Terzaghi理论适用性及预测精度进行验证：(1)小变形问题修正方法对比计算；(2)压缩系数、渗透系数保持不变的大变形固结问题；(3)固结参数随固结过程连续变化的大变形非线性固结问题。算例均采用图1土层条件。

3.1 小变形固结问题

为验证修正Terzaghi理论计算固结问题的可行性，将其与小变形固结问题计算结果进行对比，根据沉降曲线计算结果的稳定性与收敛性验证修正Terzaghi理论的可靠性。算例中，饱和粘土层厚10 m，底边界不透水不可压缩，均布荷载240 kPa，初始孔隙比e1=0.8，av=2.5×10-4kPa-1，k=6.342×10-10m/s，稳定应变量为4.8%，属于小变形固结问题。采用Terzaghi方法与分段修正方法计算结果如图4所示，其中边界条件与固结系数均不进行修正。

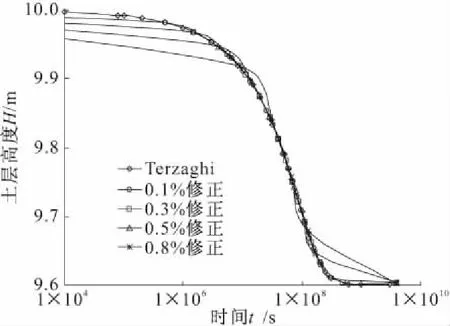
图4 小变形、线弹性固结问题

图4中小变形固结问题计算结果表明，固结参数不变情况下，采用修正Terzaghi理论固结曲线具有很好的收敛性，说明小变形条件下修正方法能够与经典理论保持一致，能够应用于小变形固结计算。

3.2 压缩性参数调整固结问题

对于大变形固结问题，固结参数在固结过程中连续变化，采用修正体积压缩系数方法修正，渗透系数在固结过程中保持不变，但固结系数连续变化。将修正理论与Terzaghi理论计算结果进行对比，根据沉降曲线计算结果的差异确定修正Terzaghi理论计算大变形固结的可行性。验证算例中，饱和粘土层厚10 m，不透水不可压缩底层，均布荷载100 kPa，初始孔隙比e1=4，av=2.0×10-5kPa-1，k=1.0×10-8m/s，稳定应变量为47%，属于大应变固结问题。采用Terzaghi方法与分段修正方法计算结果如图5所示，其中边界条件不修正为常量。

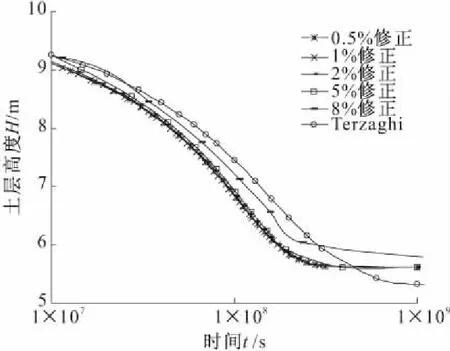
图5 压缩性修正求解大变形固结问题

图5结果表明大变形固结问题采用修正固结参数方法能够反映出土体大变形固结特性，一定程度上克服基本假定引起的计算误差。采用修正方法计算最终稳定沉降量略小于Terzaghi方法，但是修正方法达到80%固结度固结历时仅为Terzaghi方法的一半，符合大变形固结进程快于小变形的一般结论。

3.3 固结参数双修正计算

固结参数双修正方法以室内沉降柱模拟粘性泥沙沉降试验为基础，采用式(13)渗透系数、有效应力及固结参数修正公式进行固结计算。土层基本参数为：固结起始态饱和土层厚0.430 m，底层不透水不可压缩，自重固结稳定，初始孔隙比e1=11.45，Gs=2.75;初始态压缩系数av(1)=0.14 Pa-1，k(1)=5.6×10-6m/s，体积压缩系数mv(1)=0.01125 Pa-1，固结系数cv(1)=4.98×10-8m2/s，稳定应变为52%，属于大应变固结问题。固结土体采用式(7)、(8)拟幂次形式本构关系，代入方程参数进一步表达为(15)式，有效应力、渗透系数与孔隙比关系如图6(a)、(b)所示。

(15)

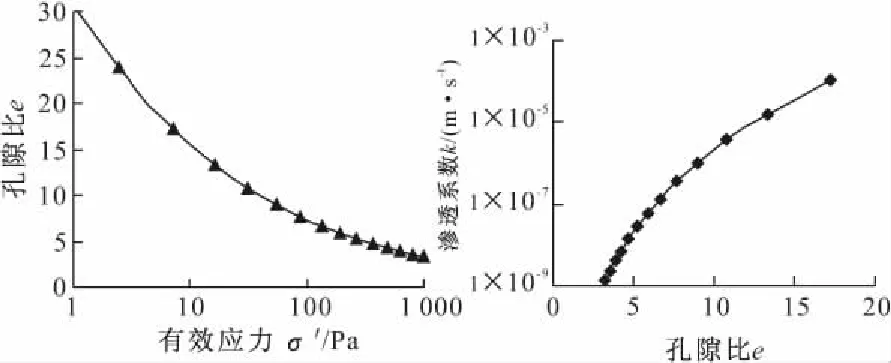
图6 土体非线性本构关系

采用Terzaghi方法与固结参数双修正方法计算结果以及沉降柱试验曲线如图7所示。计算过程中，上边界条件et=11.45保持不变，下边界条件孔隙比关于坐标的导数随固结过程根据式(14)连续调整修正。采用1%应变修正方法，自重固结孔隙比在固结过程中沿深度分布及发展曲线如图8所示。

图7 压缩性修正求解大变形固结问题

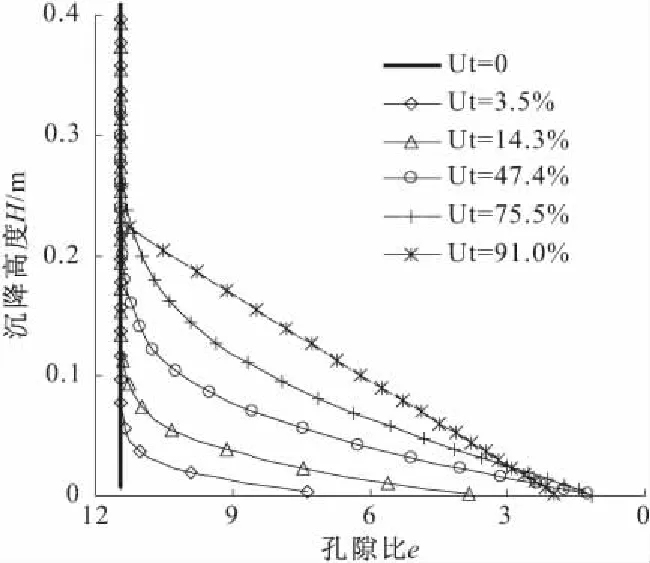
图8 孔隙比分布及固结过程中发展变化

图7实际沉降曲线与不同层次应变修正方法计算曲线及Terzaghi方法计算曲线对比表明修正Terzaghi方法能够满足土体大变形固结沉降特点及计算要求，与实际沉降曲线符合良好；经典Terzaghi理论计算结果与实际沉降曲线相差甚远，固结进程远慢于土体实际沉降进程，在大变形固结计算中存在较大误差。图8中孔隙比在固结过程中的变化规律基本满足土体自重固结过程特点，孔隙比分布与不排水下边界条件处理相关，由于边界条件在固结过程中的变化，下边界附近孔隙比在固结后期有增大膨胀现象，与土体实际情况不相符，边界条件的合理处理对提高修正Terzaghi方法的计算精度具有重要意义。

Terzaghi理论求解大变形固结问题的误差来源于沉降量引起的较大坐标误差以及固结参数在固结过程中的变异性误差，采用单一不变固结参数无法反应固结过程的非线性大变形特点。修正方法以有限应变理论分步计算为基础，应变步长满足小变形要求并根据固结进程实时进行固结参数调整修正，反映出固结参数在固结过程的非线性与变异性，扩展Terzaghi理论在大变形固结领域中的应用范围。

4 结 论

(1) Terzaghi固结方程在建立过程中不存在小变形限定，基于有限应变理论的修正Terzaghi方法在满足小变形解析计算、收敛于小变形解析解基础上能够应用于吹填土大变形固结沉降计算，计算结果反映出土体固结的大变形非线性特点，沉降预测曲线与实际沉降符合良好。

(2) 采用基于试验数据的拟幂次函数关系表征有效应力、渗透系数与孔隙比间非线性关系能够反映出固结参数在固结过程的非线性变化规律。根据三个算例的计算验证，得到修正Terzaghi方法收敛于小变形固结计算，固结参数的变化对固结进程影响巨大以及考虑双参数修正方法能够得到与实际沉降曲线相匹配计算结果的结论。

(3) 孔隙比控制变量固结方程边界条件处理是方程求解的困难所在，由于固结参数的变化，孔隙比边界条件一直改变，赋值不当极易造成较大计算误差。不排水孔隙比边界条件的处理是孔隙比变量固结计算的关键，特别是考虑吹填土体自重应力的欠固结土固结计算，这也是修正Terzaghi方法改进的方向。

(4) 应变步长对固结计算结果有较大影响，但小变形与大变形固结的分界一直没有严格限定。根据修正计算、大变形固结计算以及Terzaghi固结计算结果的对比分析确定不同土体大小变形固结界限具有重要工程意义。

[1] 魏汝龙. 从实测沉降过程推算固结系数[J]. 岩土工程学报, 1993, 15(2): 12-19.

[2] 殷宗泽. 土工原理[M]. 北京: 中国水利水电出版社, 2007.

[3] Gibson R E, Eengland G L, Hussey M J L. The theory of one dimensional consolidation of saturated clays:Ⅰ. Finite nonlinear consolidation of thin homogeneous layers[J]. Geotechnique, 1967, 17(2): 261-273.

[4] 谢康和, 郑 辉, Leo C J. 变荷载下饱和软粘土一维大应变固结解析理论[J]. 水利学报, 2003, 10(10): 1-10.

[5] Gibson R E. On Cryer’s problem with large displacements and variable permeability[J]. Geotechnique, 1990, 40(2): 627-631.

[6] 谢新宇, 朱向荣, 夏建中. 饱和土体一维大变形固结固结系数研究[J]. 浙江大学学报, 1998, 23(3): 319-324.

[7] Ducan J M.Limitations of conventional analysis of consolidation settlement [J]. Journal of Geotechnical Engineering, 1993, 119(9): 1333-1359.

[8] Mesri G,Tavenas F.Discussion of permeability and consolidation of normally consolidated soils [J]. Journal of Geotechnical Engineering Pivision, 1983, 109(6): 873-878.

[9] 方开泽, 高新科. 冲填土一维非线性固结计算[J]. 人民黄河, 1979, 10(3): 66-78.

[10] 洪振舜. 吹填土一维大变形固结计算模型[J]. 河海大学学报, 1987, 15(6): 27-36.

[11] 洪振舜. 大变形固结计算模型及定解条件的探讨[J]. 河海大学学报, 1988, 16(5): 104-112.

[12] Fox P J, Lee J, Qiu T. Model for large strain consolidation by centrifuge[J]. International Journal of Geomechanics, ASCE, 2005, 5(4): 267-275.

[13] Lucas L M. Consolidation and strength evolution of soft mud layers[D]. Delft: Delft University of Technology, 2000.

[14] 谢新宇, 朱向荣, 谢康和, 等. 饱和土体一维大变形固结理论新进展[J]. 岩土工程学报, 1997, 19(4): 30-38.

[15] 林 鹏, 许镇鸿, 徐 鹏, 等. 软土压缩过程中固结系数的研究[J]. 岩土力学, 2003, 24(1): 106-112.