基于谱分析法的半潜平台疲劳强度研究

2012-01-23

船海工程 2012年1期

关键词：谱分析海况传递函数

(海洋石油工程股份有限公司设计公司浮体设计部，天津 300451)

1 谱分析法原理

1.1 海浪及平稳随机过程

谱分析法的理论基础是随机过程理论中的线性系统变换。

船舶与海洋工程结构是一种典型的动力系统，作用在结构上的波浪过程是系统的输入，结构内由于波浪作用引起的交变应力X(t)则是系统的响应，见图1。

图1 系统输入与系统响应的关系

在一般情况下，系统的响应过程与输入过程之间的关系可写成

X(t)=L[η(t)]

(1)

式中：L——把η(t)变换成X(t)的算子。

当L为一线性算子的时候，系统就称为是线性的。本文讨论的半潜平台结构的疲劳分析，所应用的波浪载荷计算和结构分析都是基于线性理论。在这个条件下，波浪若是一个平稳的随机过程，经过变换得到的交变应力也是一个平稳的随机过程。由随机过程理论，上述两个平稳随机过程的功率谱密度之间有下列关系。

(2)

式中：H(ω)——线性动力系统的传递函数或频率响应函数；

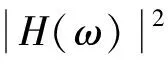
传递函数H(ω)的物理意义是，它是在线性动力系统做圆频率为ω的简单谐振时，响应过程的振幅与输入过程的振幅之比。当输入过程为波浪，响应过程为交变应力时，传递函数就是结构在圆频率为ω的规则余弦波作用下，应力幅值与波幅之比[1]。

1.2 海浪谱

海浪谱，反映的是不同频率下，各子波所具有的能量，是一种能量谱。在疲劳应力短期预报中，海浪谱十分重要，因为就海洋工程结构系统而言，不同的海浪能量输入将引起不同的输出。目前海洋工程结构疲劳评估的谱分析方法，波浪的功率谱密度多使用ISSC推荐的双参数的Pierson-Moskowitz谱(简称P-M谱)。P-M谱可以写成不同参数的表示形式，如果用有义波高Hs和平均跨零周期Tz两个参数来表示，海浪谱的表达式为

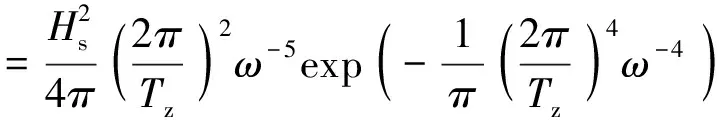
(3)

1.3 响应谱

用波浪载荷计算程序得到平台在浪向角为θ，圆频率为ω的规则波中的平台运动以及外部水动压力的响应。将外部水动压力和与平台运动有关的各种惯性力施加到平台结构有限元模型上，得到应力响应。将所得的应力幅值与波浪幅值相比就得到该浪向角和圆频率下的传递函数。

(4)

实际计算中，直接输入的是平台在单位波幅规则波中的运动响应和动压力的值，所以计算结果直接就是传递函数的值。

因此，由式(2)可以得到应力的响应谱GXX(ω)。

1.4 波浪扩散函数

上述波浪谱和响应谱都是针对长峰波的情况，即海浪来自于同一个方向。真实的海浪不只来自一个方向，而是不同方向的海浪的共同贡献，因此，还要考虑波浪的扩散性，即短峰波效应的问题，描述这种特征的函数称为波浪扩散函数。

1.5 应力范围的短期分布

在船舶与海洋工程中，海洋波浪的长期状态通常看成是由许多短期海况的序列所组成。每一海况由表征波浪特性的参数以及该海况出现的频率来描述。对每一短期海况，通常把波浪作为一个平稳正态随机过程来研究。相应地，平台结构因波浪引起的交变应力过程也可以看成是由许多短期海况的序列所组成。对于工作在海洋中的平台而言，对每一海况，给定浪向和频率，交变应力过程是一个均值为零的平稳正态过程，其相应的应力范围分布称为短期分布。根据平稳正态交变应力过程的统计特征，应力范围的短期分布可用连续的理论概率密度函数来描述。

实际应用中，一般将某一海况中在给定浪向下的交变应力过程作为均值为零的窄带平稳随机过程，则根据随机过程理论可知，其应力峰值服从Rayleigh分布，概率密度函数为

≤y<+∞

(5)

式中：y——应力峰值；

σX——交变应力过程的标准差。

1.6 应力范围的长期分布

综合所有海况的应力范围短期分布以及各海况和浪向出现的频率，就得到了应力范围的长期分布，其形式是分段连续的。平台在寿命期内遭遇的各种海况由有义波高和平均跨零周期的联合概率组成的海浪散布图来描述。根据平台工作的特定海域，使用相应的海浪散布图。

在上述条件下，应力范围的长期分布可表示为各短期分布的加权组合，其分布函数为

·pj·Fsij(S)

(6)

式中:ns——海浪散布图各短期海况总数；

nh——可能出现浪向总数；

pi——第i个海况出现的概率，取为海况分布资料中各海况出现的频率；

pj——第j个浪向出现的概率；

Fsij(S)——某一海况的概率分布函数。

1.7 疲劳累积损伤度计算

疲劳累积损伤度，可直接用各短期分布疲劳累积损伤度的组合得到，则设计寿命期的疲劳累积损伤度D为

(7)

式中：Td——平台的设计疲劳寿命；

A,m——所用S-N曲线的两个参数；

ns——海浪散布图中各短期海况总数；

pi——各海况出现的概率；

nh——可能出现的浪向总数;

pj——各浪向出现的概率；

rij——海况i和浪向j下响应平均过零与总平均响应过零率的比值；

ν0——考虑所有海况、浪向的应力响应总平均过零率。

2 应用实例

对整个模型所有的节点的粗网格疲劳结果进行大范围搜索，选取疲劳损伤大且对平台整体强度有重要作用的典型节点。使用局部模型方法对选取的节点进行局部细网格疲劳分析。以某一半潜平台cross pontoon与cone连接处为例，说明局部模型疲劳计算过程。节点在整体模型中的位置见图2。

2.1 有限元结构模型细化原则

1) 疲劳热点区域的单元形状为4节点矩形壳单元，大小为t×t，t为板厚；

2) 热点区域的t×t矩形单元，应至少向各向延伸10个单元；

3) 热点区域内的梁单元的面板和腹板均采用壳单元细化；

图2 局部模型在整体结构中的位置

4) 由细网格向粗网格过渡区域的单元尺寸尽可能平缓过渡。

局部模型和热点处细化区域网格见图3和图4。

图3 GeniE局部模型示意

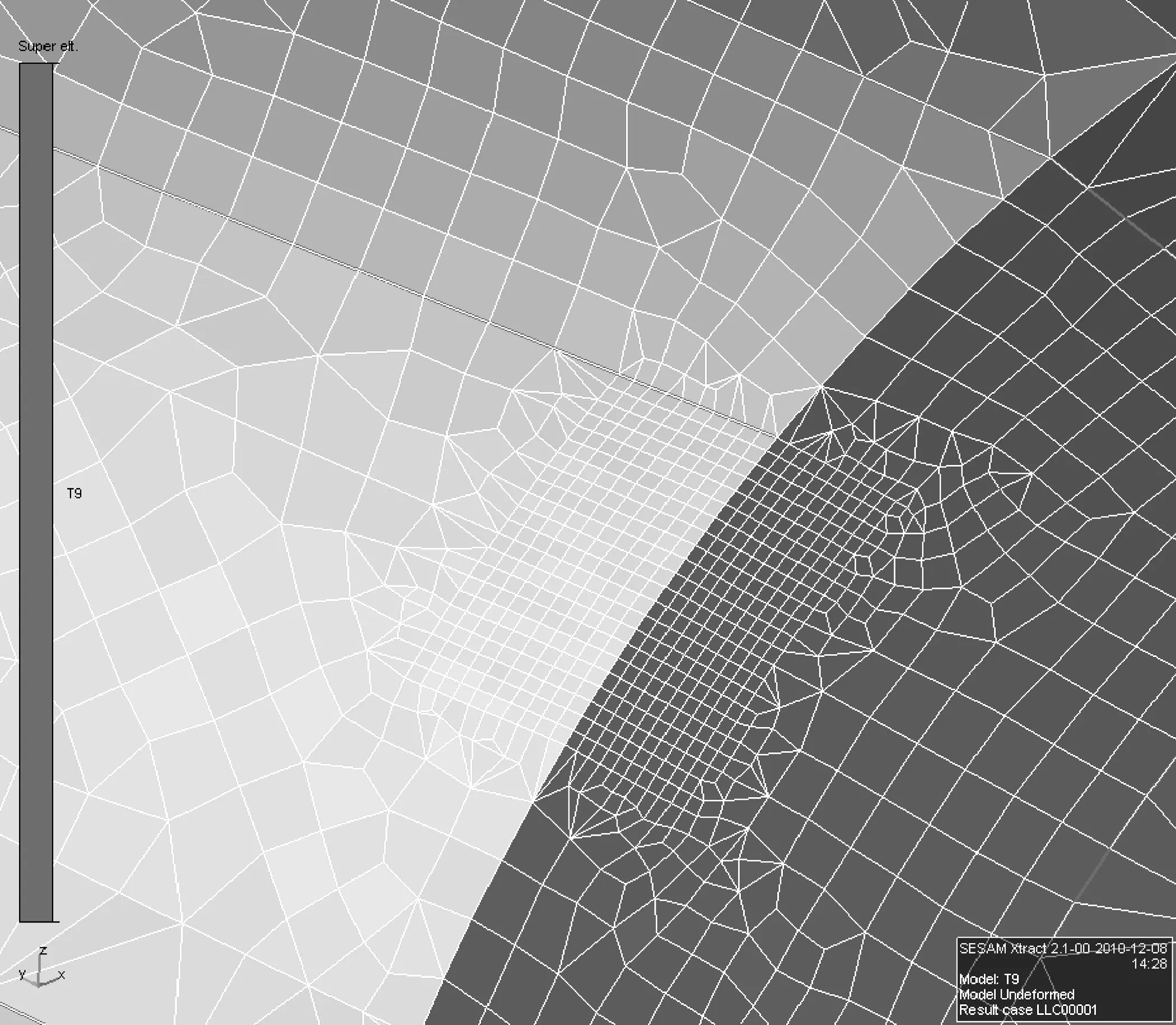
图4 热点处细化网格区域

2.2 疲劳载荷

疲劳损伤是由载荷的长期作用累积形成的，因此，选择作业工况为计算工况。

在HydroD中作如下设置。

1) 海况参数。

频域分析工况：浪向，0～360°，间隔45°；

频率，0.2～2.0 rad/s，间隔0.1 rad/s。

海况：海浪谱取P-M谱；

波浪传播主方向；

波能扩散函数。

2) 建立Panel模型(平台整体湿表面模型)，Morison模型(平台整体杆件模型)，Mass模型，以施加水动力载荷，拖曳力，惯性力载荷等。

3) 输入局部结构模型。应用Wadam程序，基于三维势流理论进行线性频域水动力分析，计算出波浪载荷和惯性力的传递函数。

2.3 局部模型边界传递

利用Submod模块，在局部模型边界处，获取整体模型相应位置处位移，使局部模型边界处的位移与整体模型位移协调一致。边界位移传递模型见图5。

为了验证位移的一致性，分别读取局部模型边界处与整体模型相应位置处若干节点的位移，见图6和图7，表明二者一致。

图5 Submod边界位移传递

图6 局部模型边界处节点位移

图7 整体模型相应位置处节点位移

2.4 局部结构计算

将Wadam计算得到的波浪载荷传递函数，通过Sestra模块，投影传递，施加到局部结构上，进行准静态有限元计算，得到疲劳应力的传递函数。

2.5 热点疲劳损伤计算

在Stofat模块中，输入海浪谱，特定工作海域散布图，波浪扩散函数，各浪向出现概率，S-N曲线等[2]，以及前一步得到的应力传递函数(R文件)，进行线性插值后，即可得到该热点焊趾处的疲劳累积损伤度。线性插值方式见图8,热点位置ccome,板厚9 mm,S-N曲线为ABS-E-CP，工作海域为中国南海，安全系数为2时疲劳计算结果为目标寿命40年，疲劳损伤度1.16，疲劳寿命34.5年。

可见，此热点处疲劳强度不满足，将板厚从19 mm增加至22 mm后，疲劳损伤降为0.92，满足疲劳强度要求。