燃气轮机转子支承刚度计算研究

，，

(海军工程大学 船舶与动力学院，武汉 430033)

燃气轮机作为高速旋转机械，其转子动力特性对燃气轮机的安全性有重要影响[1]。支承的刚性对转子的动力特性有着至关重要的影响。现代燃气轮机转子大都采用“柔轴”设计，为避开转子的临界转速及减小轴承作用力，在支承结构中大都采用了弹性阻尼支承，见图1。

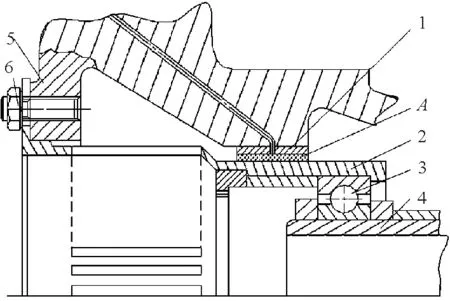
1-油膜环；2-弹性支座；3-轴承；4-转轴；5-螺栓；

弹性支座用螺栓5固定在机匣6上，悬臂地支承转子。支承的弹性来自于具有较低刚性的鼠笼条7。在转子横向载荷作用下，弹性支座上的表面A挤压油膜，起到减振作用。在燃气轮机的初步设计阶段，对支承刚度进行近似计算，使其与转子动态特性参数匹配得当非常重要[2]。燃气轮机转子支承的刚度计算必须考虑支承各结构的刚度特性，主要包括机匣、弹性支承、油膜阻尼器及轴承。

1 支承系统各组件刚度

1.1 机匣

燃气轮机机匣的支承刚度计算是一个静力学问题，可以用解析法、能量法或者有限元法求得数值解。通常由于发动机的转子支承系统结构和传力路线等很复杂，涉及的零件多，而有限元法适合求解复杂结构及边界条件，所以机匣的支承刚度多选用有限元法进行计算分析。根据线刚度的计算公式可以方便地求出机匣的径向支承刚度。

Kδ=F/δ

(1)

式中：Kδ——机匣支承的刚度系数；

F——施加在轴承外环的径向力；

δ——在F下响应的径向位移。

对于有弹性支承的转子系统的支点，机匣的刚度一般要远大于弹性支承的刚度(1个量级以上)。因而在计算采用了弹性支承结构的支承系统时，可将机匣考虑为刚性体。

1.2 弹性支承

燃气轮机转子-支承系统通常都采用弹性支承，其刚度相对于转子的刚度较低，即所谓低刚性弹性支承。这样可以使得转子系统的临界转速降低到要求的数值而不削弱转子本身的刚性，且通过临界转速时，转子的振幅和通过轴承座的外传载荷很小。图2给出的是某转子不平衡响应的幅频特性。

由图2可见，采用弹性支承后，低阶临界转速降低到发动机工作转速范围以下；而高阶临界转速则由原来刚性支承时的临界转速值提高到发动机工作转速范围以上。同时，采用阻尼器时，临界转速时的响应峰值将大大减小，从而保证发动机转子平稳地通过这些临界转速区。

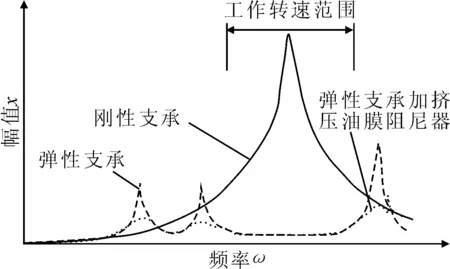
图2 转子不平衡响应的幅频特性

目前，燃气轮机上采用的弹性支承结构多种多样，主要分为笼条式和环式两类。笼条式弹性支承与弹性环式支承相比，所占空间大，质量也大，但其支承结构简单，加工和装配也方便，生产和使用经验丰富，可靠性高。笼条式弹性支承包括鼠笼式和拉杆式。它们均可以分别加挤压油膜阻尼器或其它挠度限制器构成弹性阻尼支承。

1.2.1 鼠笼式弹性支承

鼠笼式弹性支承的弹性由鼠笼条提供。由于笼条比较细长、柔软，轴承安装座及安装边与之相比，可以视为刚性固定端，见图3。

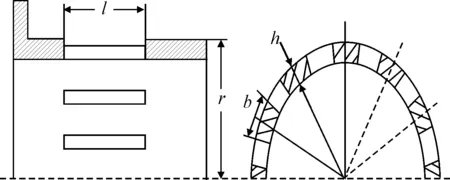
E-材料弹性模量；b-笼条截面宽度；

如果杆的数目较少，当不平衡力作用方向变化时，弹性支承的刚度瞬时可能是变化的，因而会显示出各向不均匀性。但当弹性杆数目较多时，这种各向异性就基本消失了。将笼条截面近似成矩形，得到刚度计算式[3]

(2)

式中：n——笼条数。

应用此公式应考虑以下两点[4]。

1) 由于公式推导中认为支承两端为绝对刚性，因此，只能用于计算低刚性的弹性支承。计算肋条数很多的高刚性支承，应采用有限元方法。

2) 肋条在靠近根部处必然存在圆角R，因此，按上述公式计算的刚度值要比实际刚度值偏低，可利用实验结果获得修正曲线。对计算的刚度值进行修正，可以使计算精度得到提高。

为此，文献[5]基于鼠笼弹性支承实物，分别用近似公式(1)、有限元法进行了刚度计算，并且进行了刚度试验研究。通过对试验结果的分析获得了鼠笼结构参数对刚度的影响规律，并进一步得到刚度计算修正公式。

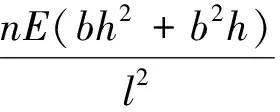
(3)

1.2.2 拉杆式弹性支承

拉杆式弹性支承与鼠笼式弹性支承原理结构基本相似，但拉杆式把矩形断面的笼条改为圆形断面的弹性杆。弹性杆两端与相邻零件的连接一般采用高温钎焊等方法，以保证连接刚度与接头的抗疲劳性能。这种弹性支承所提供的刚度计算方法与鼠笼式一样，只是其中各弹性杆的抗弯断面惯性矩与杆的位置无关。拉杆式弹性支承刚度计算式为[6]247

(4)

1.2.3 波纹环式弹性支承

图4所示为波纹环式弹性支承(又称曲杆式弹性支承)。

图4 波纹环式弹性支承

其主要弹性元件是一个在内、外表面制有相互错开的均匀分布的若干凸台的环形件——波纹环。其内表面的凸台与轴承安装座外表面配合，外表面的凸台则与支座的承力环内表面配合。在任一瞬间，波纹环上的曲杆有一半是不受力的，另一半则按正弦分布规律承受不同大小的径向力。另外，由于凸台的尺寸、圆角以及加工精度等各方面因素的影响，使得这种波纹环式弹性支承的刚度难以比较准确地计算，其近似计算公式为[6]248

(5)

式中：n——波纹环内侧或外侧的凸台数；

h——波纹环的厚度；

b——波纹环的宽度；

a——凸台长度；

Dm——波纹环的平均直径，

Dm=(D1+D2)/2；

H——凸台的厚度，H=h+s；

其中：D1、D2——波纹环的内、外直径；

s——凸台的凸出高度；

d——凸台与圆弧段的过渡圆直径。

1.3 滚动轴承

滚动轴承是一种高载荷流体动力摩擦副，不仅存在固体接触的弹性变形，而且有流体动力润滑油膜的影响，弹性变形与润滑油膜之间又相互耦合。因此，滚动轴承动力学实际上是一个流固耦合问题，必须联解耦合的流体润滑的雷诺方程、弹性变形方程及压(温)粘方程。目前只能在某些简化的假设条件下，通过数值迭代进行计算，求解这些非线性方程组。

转子动力学分析一般采用滚动轴承静刚度的统计数据，其范围为2×107～1×109N/m；或采用某些经验公式作估算[7-8]。以往形成的经验公式计算出的刚度值会因载荷等自变量的变化而产生较大的误差区间带[9]。据此由线弹性理论导出滚动轴承刚度的理论公式，并指出基于线弹性理论的理论公式中载荷等自变量的变化适用范围比经验公式要宽得多；采用具体轴承实测参数，基于赫兹接触理论导出刚度计算公式，能更好地反映实际刚度值。

1.4 挤压油膜阻尼器

高速转子支承系统成功地采用挤压油膜阻尼器的减振技术，是现代转子动力学发展中的重要成就。关于挤压油膜阻尼器的优化设计，是研究的重要领域。一定工况下，挤压油膜阻尼器具有油膜刚度和油膜阻尼，它反映了挤压油膜阻尼器的承载能力与减振能力。对于挤压油膜阻尼器的减振机理分析、实验研究和工程应用，人们进行了大量探索，建立合理的数学模型、选择使用便利的方法计算油膜反力，至今仍是这个领域有待解决的重要问题。在分析转子动力特性时，除转子-支承系统自身的刚度外，还要计及油膜刚度。Navier-Stokes方程和Reynolds方程是建立在动压润滑理论基础上的油膜运动方程，将其应用于带定心弹簧(即与弹性支承组合使用)的挤压油膜阻尼器，在π油膜假设下可以推导出等效刚度和等效阻尼计算式[10]：

(6)

(7)

式中：μ——润滑油的动力粘度系数；

R——油膜环的平均半径；

L——油膜轴承宽度；

c——油膜环间隙；

e——油膜内环圆轨迹进动的半径；

ε——偏心率；

ω——油膜环进动较频率。

2 算例

某型燃气轮机低压压气机转子的前支承采用径向止推滚珠轴承，由鼠笼式弹性支承、挤压油膜阻尼器和滚珠轴承组成，计算支承刚度。相关参数见表1、2。

表1 轴承结构参数

表2 鼠笼支承结构参数

对于采用弹性支承的转子系统，可以将支承模化为两自由度的振动模型，其等效刚度Keq为

(8)

式中：Kb——滚动轴承刚度；

Ks——弹性支承刚度。

根据相关参数对该燃气轮机前支承刚度进行计算。

1) 滚动轴承刚度。分别利用文献[9]给出的刚度改进公式(9)及经验公式(10)：

(9)

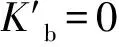
(10)

计算得到滚珠轴承的刚度值为

Kb=2.645×108N/m，

二者误差为4.27%。

2) 弹性支承刚度。鼠笼弹性支承刚度的计算采用式(2)，计算得Ks=2.158×107N/m。

3) 总刚度。将经验公式计算的轴承刚度和鼠笼刚度带入式(7)得到前支承总等效刚度为Keq=2.001×107N/m。

文献[11]给出了该型燃气轮机转子前支承刚度值为1.899×107N/m，误差为+5.4%，误差处在初步设计允许范围之内。

3 结论

1) 采用某型燃气轮机前支承实际结构参数对支承刚度进行计算，对比相关文献结果，对于该结构的弹性阻尼支承系统，刚度值在一定精度范围内的初步计算可不考虑油膜刚度的影响。

2) 随着计算和测试技术的发展，对于支承刚度更准确的计算，可通过试验修正经验公式，进而获取考虑油膜刚度影响时的系统等效刚度。

[1] 晏砺堂.航空燃气轮机振动和减振[M].北京: 国防工业大学出版社,1991.

[2] 闻邦椿,顾家柳,夏松波,等.高等转子动力学[M].北京: 机械工业出版社,2000.

[3] Vo00016航空发动机设计手册总编委会.航空发动机设计手册：第19册——转子动力学及整机振动[M].北京：航空工业出版社,2000.

[4] 张大义,母国新, 洪 杰.航空发动机转子支承系统刚度计算中的几个问题[J].战术导弹技术,2005(2):20-23.

[5] 徐方程.燃气轮机转子-鼠笼-挤压油膜阻尼器动力学特性研究[D].哈尔滨:哈尔滨工业大学,2009.

[6] 顾家柳,丁奎元,刘启洲,等.转子动力学[M].北京:国防工业出版社,1985.

[7] 陈 忠.滚动轴承及其支承的刚度计算[J].煤矿机械,2006,27(3):387-388.

[8] LIU J G,UWE F,ANDREAS S.Accuracy improvement of impedance measurements by using the self-calibration [J]. Measurement J. of the International Measurement Confederation,1999,25(3):213-225.

[9] 王 刚,郭茂林.航天航空滚动轴承刚度[J].哈尔滨工业大学学报,2001,33(5):644-645.

[10] MUSZYSKA A.Whirl and whip rotor/bearing stability problems[J].Journal of Sound and Vibration,1986,110(3):443-453.

[11] 关 琦,金 鹤,新 力.某型燃气轮机低压涡轮压气机转子动力学分析[J].舰船科学技术,2010,32(8):127-145.