供应链协同下的库存成本优化及分配分析研究

马斌，宋以楠

（太原理工大学经济管理学院，山西太原030024）

现代企业正处于一个不可预测、复杂多变、竞争激烈的环境，高新技术的出现和更迭瞬息万变，产品的生命周期越来越短；消费者成为市场需求的主导，消费者的多样化、现代化、个性化产品需求给企业的运营方式带来了新的挑战与新的机遇；人们生活质量的提高和市场环境的变化，向企业提出了更高的生产与服务要求等。传统的供应链已经不能满足客户对产品质量和服务水平提高，对响应时间缩短的要求，大部分的企业开始意识到它们不能独立的在企业间的竞争中获得优势，而应该与整个商业联盟的成员共同合作来得到利润最大化。因此供应链协同就成为解决现在企业问题的最有效方法，并且已经成为供应链管理里面的最前沿的研究课题。

供应链协同是在继VMI、CPFR、连续补充等一系列战略思想不断出现后，由咨询界和学术界正式提出来的。供应链协同是指供应链中各节点企业为了提高供应链的整体竞争力而进行的彼此协调和相互促进，是针对供应链网络内各职能成员间的合作所进行的管理。［1］

供应链协同下库存管理模式就在于追求整个供应链的整体效率和系统费用的最优化，使供应链系统总成本降至最低，能够使供应链上的企业获得并保持稳定持久的竞争优势，进而提高供应链的整体竞争力。

但当前，供应链协同管理下成本管理研究还存在不足。它没有给出整条供应链的最优成本，只是分别对各阶段的库存成本进行最优化。目前对供应链协同管理的库存成本分析和优化的研究比较少，还没有比较详尽的对比分析。本文的研究目的是提供一套科学的供应链分配方法。以供应链整体效益最低为研究基础，利用相应的成本分析法，通过对比供应链协同前后库存管理的成本，分析方法的有效性，在此基础上利用效用函数对供应链中成员进行利润分配，为供应链协同提供决策依据。

一、库存成本模型

库存以不同形式 （原材料、在制品、半成品、产成品）存在于供应链的各个环节中，供应链管理中库存控制具有举足轻重的地位。持有库存决策量对于整个供应链中各个企业的成本决策都有重大影响。供应链管理的目的在于提高整体系统效率和整个系统的费用有效性，使供应链总成本达到最小，其中包括供应链中的库存成本。［2］所以，供应链管理并不是简单地使库存或运输配送成本达到最小，应该运用更科学更系统的方法进行运行与管理。综合以上所述，本文采取对比的方法比较供应链协同管理前后供应商和制造商库存的成本变化，由此可证明供应链协同管理的必要性，并以此作为供应链协同的定量化依据。

基于供应链协同的库存成本对库存整体上进行管理，而不是单单对供应链上各个节点分别管理。当供应商、制造商、分销商合作决定产量和最终价格时，可以将供应链看做一个整体，一个组织，供应链上各组织的目的是实现整个供应链的利润最大化。

（一）模型参数定义 （见表1）

（二）假设

本文在建立模型的过程中，不失一般性，只研究一个供应商和一个制造商组成的供应链，并且制造商采用连续库存补充 （Q，r）订货策略，订货提前期为零，补货瞬时完成。［3］由于供应链协同后信息共享程度高，协同制造商的后缺货成本和供应商的处理成本大大降低，符合本文结论。所以本文假设无缺货和损耗。

表1 参数定义

（三）模型建立

供应商则采用经济生产量（Economic Production Quantity，EPQ），制造商根据成本最小化计算经济订货量（Economic Order Quantity，EOQ）。为不失一般性，本文采用该模型的计算原则对传统供应链与协同后的供应链进行模型的推导和对比分析。

在传统供应链情况下，制造商的库存成本为

供应商的库存成本为

在供应链协同前，制造商根据自己库存成本最低原则决定采购量Q，即

得

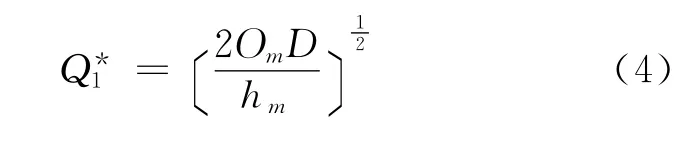
供应链协同前，其供应链的库存成本就是供应商与制造商库存成本简单的相加，所以供应链协同前供应链总成本为：

在供应链协同后，供应链所有成员采用成本最低原则决定采购量，制造商与供应商共同管理库存，即以整个供应链的成本为基准进行库存决策。这时制造商不用耗费过多精力和金钱来对库存进行管理，也不用耗费订购成本、维持成本甚至缺货费用，在资金得到极大利用的同时还充分地满足顾客需求，供应商一次订单的处理成本就变为原先分别处理的合并费用，单位商品维持成本同样处理。而且在供应商同时管理两个仓库的同时，产品的磨损或变质基本不会存在，所以可以忽略对供应链的影响。［6］

得：

所以在供应链协同后，供应链总成本为

对比供应链协同前后供应链的库存成本，由公式 （5）和公式 （8）可得

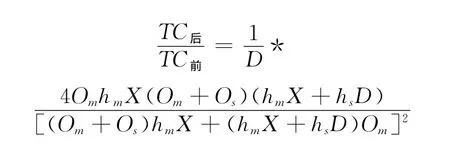
因为D≥1，此时只需比较分母-分子是否大于等于0，即

由此可知

TM后≤TM前

即供应链协同下，供应链的总成本小于传统供应链的总成本。

供应链协同后，供应商和制造商的合作使得供应链管理达到理想状态。在这种形式下，既不单纯从供应商的角度考虑也不单纯从制造商的角度考虑，而是从整个供应链的集成角度来决定供应商的生产批量和制造商的订购批量，从而使整个供应链的总库存成本最小。

（四）算例分析与问题

相关参数取值如表2：

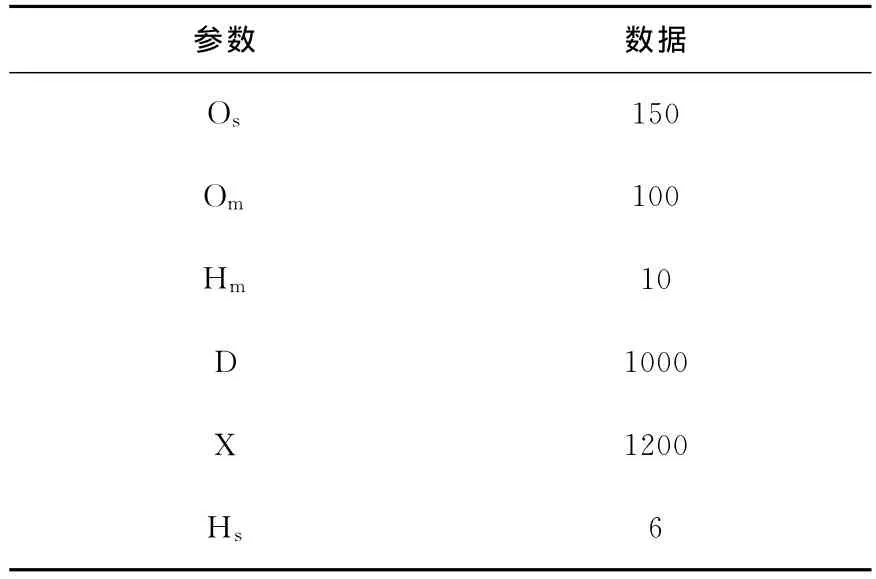
表2 参数取值表

通过计算可得，供应链协同前供应商库存成本为1414，制造商的库存成本为1414，整个供应链的库存成本是2828。供应链协同后供应链的总库存成本为866，远远小于供应链协同前的库存成本。

二级供应链协同管理下，原来各自管理库存的供应商和制造商共同管理库存。从供应链层面实现库存管理的最优化，更大程度地减少了库存管理的费用，优化了整体供应链的库存成本，对供应链的好处不言而喻，不但可以节省企业在库存上的管理费用，也可以把这部分的资金用于企业周转，实现更具柔性和竞争力的供应链，而且企业更容易实现如敏捷制造，精益生产，准时制生产 （JIT）等先进的管理思想，使企业能更大程度满足客户需求。

由算例分析可知供应链协同后，供应链的整体库存成本由2888缩减到866。可以看到供应链协同后，制造商的库存成本和供应商的库存成本大幅度缩减，达到了协同后的预期效果，使整个供应链的协调性和竞争能力得到了很大幅度的提高。

应注意到，制造商在供应链协同后减少了对库存的持有成本、订货成本和维护成本。这些成本都转移到了供应商，在供应商理性选择下，可能不愿意参加供应链协同，这样供应链库存成本最优就很难实现。解决这个问题的有效路径之一就是转移支付，制造商对供应商进行转移支付，这样就会大大提高供应商参与供应链协同的积极性。［4］

二、基于转移支付的协调策略

企业获得利润的过程也就是整个供应链获得的利润在参与企业中进行分配的过程。为缩小二级供应链因为供应链协同运作下带来的供应商单方面的库存损失，避免整体供应链资金分配不合理，这就需要转移支付来解决这些问题。以达到解决供应商与制造商因利润分配不均而引发的矛盾，来提高整体供应链长期的柔性和竞争性。

转移支付（Transfer Payments）的经济思想在西方经济学中由来已久，原意是 “转移”、“转帐”，美国经济学家格林沃尔德将转移支付定义为 “政府或企业的一种不以取得商品或劳务补偿的支出”。转移支付有很多形式，本文以效用函数来确定转移支付量。［5］

（一）建立效用函数

我们可以使用 “效用”这样一个概念来定量供应商和制造商的支付决策对风险偏好和厌恶的程度，衡量不同人主观上对同一期望值的价值。效用以度量决策分析中各种可能结果，使之能在数量上进行比较。在运用效用理论进行决策分析时，要根据决策者的效用函数 （效用曲线）来计算各方案可能结果的加权期望效用值，以最大的期望效用值作为选择方案的依据。

设成本转移的各可行方案有多种可能的结果值 （收益值）c，依据供应商的主观愿望和价值取向，每个结果值对供应商均有不同的价值和作用。记u＝u（c）为效用，反映结果值对供应商价值和作用大小的量值。

（二）测定效用值

设有转移支付决策系统，其收益值集合为V＝｛c1，c2，……cn｝，记c＊≥max｛c1，c2，……cn｝为最大收益，c0≤min｛c1，c2，……cn｝为最小收益，测定各收益cj的效用值u（cj），步骤如下：

1.设u（c＊）＝1，u（c0）＝0。

2.建立简单事态体L＝ ［c＊，x；c0，（1-x）］，其中x称为可调概率。

3.通过反复对供应商和制造商的提问，不断改变可调概率值x，让决策者权衡比较，当x＝pj，L＝［c＊，pj；c0，（1-pj）］时，得到无差异关系：

cj～L＝［c＊，pj；c0，（1-pj）］。

4.测得结果值cj的效用：

u（cj）＝pju（c＊）＋（1-pj）u（c0）＝pj。

不难看出，cj的效用值就等于概率值pj。

（三）测定效用值绘制效用函数曲线

换一个角度来讲，我们设效用函数的自变量x为决策过程中的损益值，函数u（x）是在决策者心中的效用值。首先确定A、B两个方案，询问决策者选择哪个方案。选择A方案代表决策者可能以概率p得到m元，后者以 （1-p）的概率无获得。选择B方案则可以无任何风险获得m／2元，且m＞m／2＞0。

在某条件下，决策者可以视为A、B方案等价，即

m／2～L＝［m，pj；0，（1-pj）］

第一步，提问：当p为多少时，以概率p获得m及以（1-p）概率无获得与确定获得m／2等价？假设决策者回答p＝0.7，则

u（m／2）＝pu（m）＋（1-p）u（0）＝0.7＊1＋0.3＊0＝0.7

分别在图中 （m／2，0.7）处作横纵轴的平行虚线交于点E。

第二步，提问：当p为多少时，以概率p获得m／2及以（1-p）概率无获得与确定获得m／4等价？假设决策者回答p＝0.4，则

u（m／4）＝pu（m／2）＋（1-p）u（0）＝0.4＊1＋0.6＊0＝0.4

分别在图中 （m／4，0.4）处作横纵轴的平行虚线交于点D。同样的步骤可以作出点F，连接各点则为该决策主体的效用函数曲线。

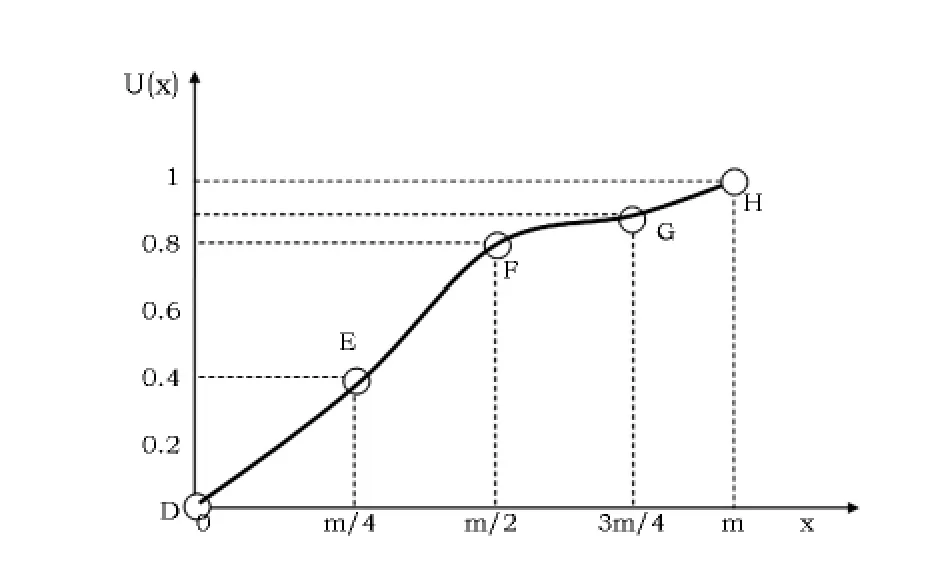
图1 效用值测定过程示意图

根据效用函数的原理，在只有一个供应商和制造商的二级供应链中，制造商应用询问的方法绘制供应商在库存上的得失的效用函数曲线，再以供应商在整体供应链中控制库存的表现为基准，对应效用函数，确定制造商应支付供应商的转移支付量。

（四）效用函数类型

制造商在绘制供应商的效用曲线时会得到以下三种曲线，对应的曲线可表现出供应商对收益的关注程度和对得失的风险保有什么样的态度。

一般效用函数分为中立型效用函数、保守型效用函数和冒险型效用函数。［7］

（1）中立型效用函数：设有效用函数u＝u（x），若结果值x1＜x2，有

由函数可知，此效用函数表明效用与结果值呈线性关系，表明决策主体对风险持有中立的态度。

（2）保守型效用函数：设有效用函数u＝u（x），若结果值x1＜x2，有

该效用函数表明随着结果值的增加效用值也递增，但递增速度随着结果值的增加而下降，说明决策主体对亏损十分敏感。

（3）冒险型效用函数：设有效用函数u＝u（x），若结果值x1＜x2，有

该效用函数表明随着结果值的增加效用值也递增，但递增速度随着结果值的增加越来越大，说明决策主体对收益十分关注。

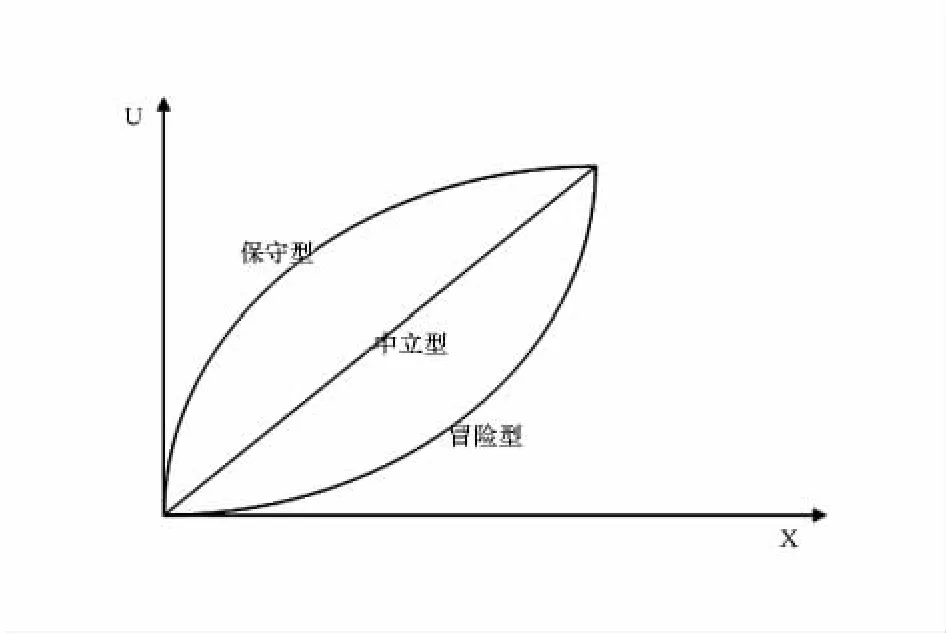
图2 效用函数类型

从图中可知，尽管效用函数不相同，但可分为线性、凹和凸三种效用函数。中立型曲线反映的是一种中间型的供应商，其效用曲线是线性的，他们完全按照期望收益准则选择方案，其风险是中性的，供应商对风险保持中立的态度。保守型曲线所反映的供应商的特点认为稳得一个收益值的效用要大于有风险的相同甚至更大的期望收益值的效用。随着结果值的增加效用值也递增，但递增速度随着结果值的增加而下降，说明这类供应商对亏损十分敏感。保守型的供应商对供应链协同后能获得的额外收益反应比较迟缓，而对因此而获得损失比较敏感，这类供应商对风险的态度是规避的，从事谨慎。冒险型曲线的供应商的特点与保守型正好相反，随着结果值的增加效用值也递增，但递增速度随着结果值的增加越来越大，说明供应商对收益十分关注。他把注意力主要放在收益上，这类供应商不怕风险，谋求更大利润。

（五）确定转移支付量

在这三类中，不论哪种类型的供应商，制造商在供应链协同下库存管理过程中对供应商的各种指标完成率进行客观评价，根据打分情况给供应商分配适当的效用值，从而利用上述等式求得相应的收益值，这个收益值就是制造商给供应商的转移支付额。

首先确定供应商决策的各个方案的损益值x。

应用期望值算子有以下几种表达：

这就标识具有凹效用函数特性的供应商决策主体可用分布效用值去替代一个非随机性的分布后果的效用值。由此可得，供应商决策主体肯定能得到一个后果值，这个后果值的效用值和分布效用值相等价，该后果值即等价确定值CE为：

则π（x）＝E（x）-CE（x）表示供应商决策主体接受此补偿后，愿意视两者为等价。所以制造商可以根据π（x）对供应商进行补偿。［7］

采用效用函数作为转移支付量确定的依据，很好的解决了供应商与制造商之间的成本转移问题，即由制造商对供应商定期测评并得到其效用函数，在供应链协同管理的过程中供应商的业绩表现确定制造商要满足供应商的效用值，从而得到相应的转移支付量。

四、结论

可见供应链协同给整个供应链中的企业带来的好处非常明显，供应链整体的库存成本也得到了优化，使供应链中的企业能更快适应市场变化，更具有柔性，在竞争中展现更大的优势。供应商在供应链协同下会管理制造商库存，使得本身库存有所增加，但是整体供应链的库存成本大大降低，为提高供应商与供应链协同，制造商就要对供应商进行转移支付。本文的局限性是只研究了二级供应链，在供应链中还有零售商，分销商等没有考虑，再者就是本文只是从成本的角度来进行对比分析，实际供应链中还应该考虑到牛鞭效应和客户服务水平等绩效评价指标。

［1］张广霞.联合库存管理法在供应链库存控制中的应用［J］.中国市场，2008，15（14）：14-15.

［2］Bernhard J.Angerhofer，Marios C.Angelides，A model and a performance measurement system for collaborative supply chains［J］.Decision Support Systems，2005.

［3］李建军.供应商管理库存（VMI）的实施研究［J］.商业研究，2007（3）：107-109.

［4］THANGAM A，UTHAYAKUMAR R.A two-level supply chain with partial backordering and approximated poisson demand［J］.European Journal of Operational Research，2008，187（1）：228-242.

［5］Nozick L K.Turnquist M A.A two-echelon inventory allocation and distribution center location analysis［J］.Transportation Research Part E，2001（37）：425-441.

［6］徐琪，徐福缘.供需网的一个节点：供应链协同管理与决策 ［J］.系统工程理论与实践，2003（8）：31-35.

［7］张所地.管理决策论 ［M］.北京：中国科学技术出版社，2005：1.