基于古诺模型的产业集群知识转移分析
2012-01-22邱俊芳
邱俊芳
(中国矿业大学管理学院,江苏徐州221000)
产业集群是在相同的产业领域内互相联系的企业和机构聚集在地理位置上邻近的地方的一种产业形态。主要包括相互依赖性很强的企业 (供应链上的同质的企业和上下游企业)、知识生产机构 (大学、研究机构和工程设计公司)、中介机构 (经纪人和咨询顾问)。对于知识而言,产业集群是具有创造、共享、转移知识能力的特殊区域创新网络。王缉慈[1]认为,产业集群促进了知识转移与流通:其一地理位置上的邻近,便于企业、机构之间面对面地接触,使企业容易寻找到所需要的知识源,降低了知识的搜索成本。其二业务上的相似性,便于产业集群内知识的传播者之间的沟通与理解,促进集群内组织间正式和非正式的交流,降低了知识转移的交易成本。
当前,知识是企业取得竞争优势的最主要资源,而产业集群竞争力同样源自知识。如何建立产业集群良好的知识转移机制,推动知识与信息的流动已经成为产业集群研究的热点问题。马歇尔分析集群形成原因,提出了知识溢出是企业集群产生与发展的驱动力;Dayasindhu以印度软件产业集群为例,研究了产业集群和知识转移问题;张生太和段新民运用系统动力学方法,建立了企业集团成员之间隐性知识传播的微分动力学模型;卢兵等在此基础上建立了组织间隐性知识转移的微分动力学模型;王娟茹运用博弈论建立了基于企业集群的隐性知识转移模型。[2~6]但是现有的产业集群及知识转移研究,很少通过定量的方法分析集群内组织间知识转移发生的原因。本文假设每个企业都在追求其个体的利益最大化的前提下,以古诺模型为基础,根据产业集群内企业知识转移的投入 (主要包括知识成本)和知识转移所取得的收益 (主要包括企业战略目标完成、业务量增长、市场份额增加以及生产成本和交易成本降低等),建立一个二阶段博弈模型,来分析集群内企业在知识转移中如何决策,以及决策条件和效果。
一、古诺模型
假设产业集群中有n个同质企业,生产和销售相同产品。市场对某种产品的容量是有限的,因此市场出清某产品的价格P (可以将产品全部卖出去的价格)是投放到市场上该产品总量Q的减函数。即(a为常数)。为了使问题简化,现以2个企业为例来研究。假设产业集群内厂商1和厂商2独立确定本企业某产品的产量,生产前两厂商不进行相互协商,也不受彼此生产的限制,并且他们是在同一时间决定本企业该产品的产量。假设这2个企业某种产品产量分别为q1和q2,那么该产品市场出清价格p=p(Q)=a-q1-q2,两厂商的此产品单位生产成本分别为c1和c2,他们同时决策各自的产量,那么各自的得益为ui=qi(a-q1-q2)-ciqi(i=1,2)。
此古诺模型存在唯一Nash均衡解。[7]
二、集群内企业间知识转移模型分析
(一)集群内企业间知识转移模型
假定企业1是知识高位势企业,进行知识移出,企业2是知识低位势企业,进行知识的移入。由于不同企业的知识含量不同,每个企业的单位成本不同,集群内企业通过知识转移,获得知识,以降低本企业产品的成本,降低的幅度大小取决于企业在知识转移中获取新知识的量。R2(Z)是企业2转移到新知识Z带来的单位产品成本降低函数。
R2(Z)函数为二阶可微的凹函数,满足:
1)Z≠0时,0<R2(Z)<1;
2)Z=0时,R2(Z)=0;
3)Z≥0时,R2′(Z)>0,R2″(Z)<0。
假设新知识Z的成本函数是M (Z),则c1=c1;c2=c2-c2R2(Z)。则根据古诺模型,这两个企业的利润函数为:
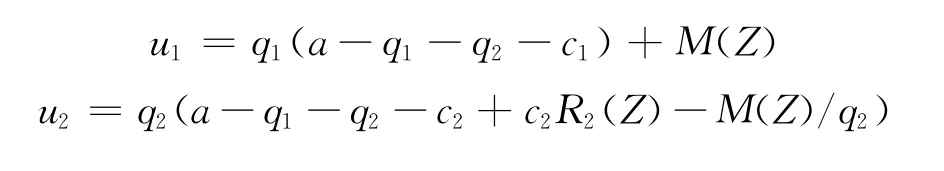
(二)博弈分析
产业集群内企业间知识转移可以看作一个二阶段博弈过程,第一阶段为知识转移阶段,第二阶段为产品市场竞争阶段。可以运用逆序归纳法来求解子博弈纳什均衡,首先求解第2阶段也就是产品市场竞争阶段古诺模型的纳什均衡,然后再求解第1阶段也就是知识转移阶段博弈的纳什均衡。
1.产品市场竞争阶段
第2阶段是产品竞争阶段,在此阶段产业集群内同质企业面对市场需求,进行非合作古诺生产竞争。无论在第1阶段的决策是什么,也就是说无论是否进行知识转移,在第2阶段两企业都独立决定自己产品的产量。此阶段是一个静态非零和博弈,存在纳什均衡。使企业1、企业2的利润(对产量)一阶条件

联立 (1)、(2)解得第2段的古诺竞争纳什均衡产量
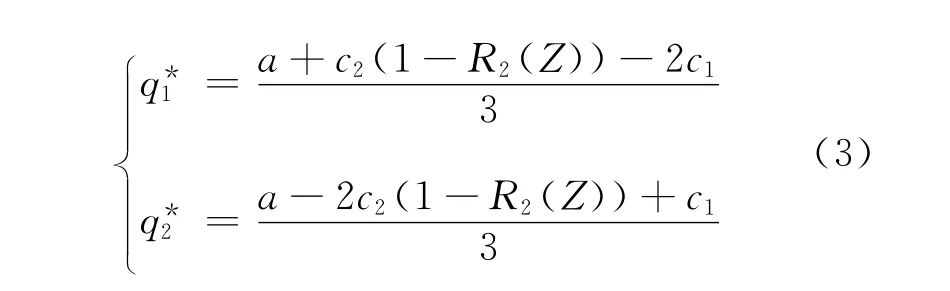
由此看出,产业集群内同质企业的均衡产量,要受到知识转移的影响。不仅与自身知识投入量、自身吸收新知识的能力以及应用新知识减少成本的能力有关,同时与对手企业获取新知识,应用新知识减少成本有关。自身知识转移得到的新知识使产品成本降低越大,则产量越高,而对手得到新知识使产品成本降低越大则自己产量降低。
由(3)可得:

从以上结果可知,产业集群内企业的产量只与企业单位产品的成本有关,企业的单位产品成本越高则该企业的产品产量越低。采用新的知识可以降低企业单位产品的成本,从而可以提高产品的产量。
将 (3)式代入 (1)、(2)式可以得到企业1和企业2的利润。
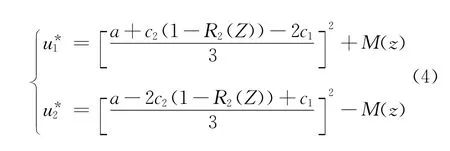
2.知识转移阶段
在完全信息条件下,产业集群内企业1和企业2双方根据以上第2阶段的博弈结果,在第1阶段同时决策各自的知识转移水平Z。影响产业集群内企业知识转移水平的因素有很多,一般不论是作为处于知识高位势的知识移出方,还是作为处于知识低位势的知识移入方,在进行知识转移水平Z决策时,主要考虑2个方面的因素:(1)产品的产量规模;(2)知识转移后本企业的利润。
(1)以产品的产量规模为博弈目标
对于处于知识高位势的企业c1而言,在博弈第二阶段产品市场竞争阶段的均衡产量是。其与企业c1是否进行知识移出无关,而与企业c2是否有知识移入有关,如果c2有知识移入,则企业c1的产品产量规模会减小。当R2(Z)=0时,即c2没有知识移入时,c1的产量最高。
对于处于知识低位势的企业c2而言,在博弈第二阶段产品市场竞争阶段的均衡产量是=。其与企业c1是否有知识移出无关,而与企业c2的知识移入有关,由于0≤R2(Z)<1,则q2的值增大,即企业c2产量规模会增大。当移入的知识,使得企业c2产品单位成本最低时,企业c2有最大产品产量。
由此可见,产业集群中企业,如果以扩大产品产量规模为目标,其必然要进行知识移入,掌握集群中最先进的知识,使产品的单位成本降到最低。这样就可以达到产品产量的最大规模。
(2)以知识转移后企业的利润为博弈目标
对于处于知识高位势的企业c1而言,要使企业利润最大,就是使取得最大值。而=0时,取得最大值。这里如果企业c2所移入的知识并不是c1所移出的知识,那么= 0,即是M′(Z)=0,那么M(Z)是一个与Z无关的常数时,企业c1取得最大利润。如果企业c2所移入的知识即是c1所移出的知识,即,+ M′(z)=0时,c2取得最大利润。
为简单起见,设R2(Z)是Z的线性函数,M(Z)是Z的线函数,即R2(Z)=R2Z,则:=。得到:
对于处于知识高位势的企业c1而言,要使企业利润最大,其转移的知识量Z应该满足。如果<0,则企业c1没有输出动力;>0,则当Z达到之前,企业c1有知识继续移出的动力,到达后输出动力减小。
对于处于知识低位势的企业c2而言,要使企业利润最大,就是使取得最大值。而= 0 时,取 得 最 大 值。-M′(z)=0时取得最大值。
为简单起见,设R2(Z)是Z的线性函数,M(Z)是Z的线函数,即R2(Z)=R2Z,M(Z)=MZ,则:
对于处于知识低位势的企业c2而言,要使企业利润最大,其转移的知识量Z应该满足。如果<0,则企业c2没有知识输入动力;>0,则Z达到之前,企业c2有知识继续移入的动力,达到之后输入动力减小。
三、结论
本文通过两阶段博弈分析,得到产业集群内企业之间知识移出与知识移入对企业产品产量、价格、收益影响,从而得到产业集群知识低位势企业知识移入和知识高位势企业知识移出的原因与动力。可以得出以下结论:产业集群内企业如果以产品产量规模为目标,知识低位势的企业必然进行知识移入。知识高位势企业,必然对同质企业减少知识输出,而对上下游企业知识输出没有影响。集群内企业如果是以取得最大利润为目标,知识输出企业,对于上下游企业始终保持知识输出动力。对同质企业知识输出,有一个最优评判,可以确定一个最优知识输出目标。而知识输入企业根据知识的价格与知识产生的效益也有一个最优评判,可以确定一个最优知识输入目标。应该指出的是,产业集群内知识转移应该是多个企业之间的博弈,本文为了研究方便,只选取了产业集群中两家企业之间的知识转移进行分析,同时没有能对新知识带来的单位产品成本降低函数进行具体分析,以至,只能分析出知识转移成本降低函数对均衡利润的影响,而不能得出准确的知识移出、移入与价格之间的关系。因此为了使模型更加接近实际情况,还需要作进一步的探讨。
[1]王缉慈.创新的空间:企业集群与区域发展 [M].北京:北京大学出版社,2001.
[2]Robert W.Helsley,William C.Strange.Knowledge barter in cities[J].Journal of Urban Economis,2004.
[3]N.Dayasindhu.Embeddedness,knowledge transfer,industry clusters and global competitiveness:a case study of the Indian software industry[J].Technovation,2002.
[4]王娟茹.基于企业集群的隐性知识转移模型[J].管理工程学报,2007(4):35-38.
[5]张生太,段兴民.企业集团的隐性知识传播模型研究 [J].系统工程,2004(4):62-69.
[6]卢兵,岳亮,廖貅武.组织间隐性知识转移的微分动力学模型 [J].系统工程,2005(11):44-48.
[7]谢识予.纳什均衡论 [M].上海:上海财经大学出版社,1999.
