双向密加筋板强度公式的推导及其修正
2012-01-22,
,
(武汉理工大学 交通学院,武汉 430063)
高速化和轻型化已成为船舶制造的发展趋势。减小板的厚度对减轻结构重量效果显著,但由此会引起板的稳定性、局部强度、局部振动性态的下降,焊接变形增大。针对这些问题,目前高速船广泛采用了双向密加筋板船体结构这种形式。由于双向密加筋板结构形式和常规的结构形式不同,故设计中多根据设计者的经验预选有关构件,再采用有限元方法进行强度校核。这既给设计者带来诸多不便,也带有较多的人为因素影响[1]。本文通过将双向密加筋板模型简化为正交异性板模型,将平衡方程进行无因次变换,最终利用各向同性板的弯曲要素表来确定双向密加筋板中的最大应力值。
1 板材料属性的转换
运用力学方法,将纵、横筋等效分摊在板上,从而将双向密加筋板等效为理想的正交异性板。
1.1 符号含义
Asx、Asy——x、y方向筋的截面积;
nsx、nsy——x、y方向加筋数;
L、B、t——加筋板的长、宽、板厚;
νxy(νyx)——x(y)方向伸长在y(x)方向收缩的泊松比;
Gxy——两个主方向x、y间夹角变化的剪切模数;
Dx、Dy——正交异性板x、y方向的抗弯刚度;
Ix、Iy——x、y方向加筋对中性轴的惯性矩;
zox、zoy——板中面到x、y方向加筋带板中性轴的距离;
twx、twy——x、y方向加筋腹板的厚度;
hwx、hwy——x、y方向加筋腹板的高度;
bfx、tfx——x方向加筋翼板的宽度、厚度;
H——正交异性板的有效扭转刚度;
M1、M2——正交异性板x、y方向最大弯矩;
Mx、My——各向同性板x、y方向最大弯矩。
1.2 弹性模量转换
(1)
(2)
1.3 抗弯刚度和抗扭转换
(3)
(4)
(5)
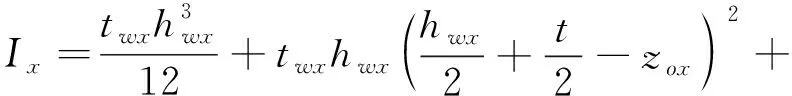

(6)
(7)
(8)
(9)
(10)
(11)
当为各向同性板时,则有
(12)
1.4 泊松比转换
根据Betti能量互换定律的推理,作用在x方向的力使y方向发生的变形,等于作用在y方向的力使x方向发生的变形,则有:
(13)

(14)


2 双向密加筋板强度公式推导及分析
2.1 强度公式推导
在均布载荷q作用下,正交异性板的弯曲微分方程式为
(15)
则式(15)转换为
(16)

(17)
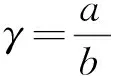
(18)
比较(18)和(19)可知,当γ1=γ2,即
(19)
时,正交异性板的弯曲要素可以借助各向同性板的弯曲要素准确地决定。当等式(19)不满足时,对于正交异性板的近似解可以选出某个各向同性板的计算边长比γ,借助于它使得正交异性板的弯曲要素以最小误差决定。因此,设
w0=w1+w2
(20)
式中:w0——正交异性板挠函数(无因次函数);
w1——各向同性板挠函数(无因次函数);
w2——修正值(无因次函数)。
将式(20)代入式(18)有
(21)
因为函数w1由方程式
(22)
决定,所以(21)减去(22)后,得到有关w2的方程
(23)
所选择的计算边长比必须使得修正值w2为最小。对于一般的密加筋板而言,可近似认为γ1和γ2足够接近,此修正值很小。采用伽辽金法来决定γ[3],让式(23)在第一次近似中的解恒等于零,得

(24)
将w1按照满足相应边界条件展开成三角级数的第一项,沿整个周界刚性固定的板有
w1=f1(1-cos2πε)(1-cos2πη)
(25)
(26)
将应力转换为无因次坐标形式为
(27)
(28)

利用各向同性板的弯曲要素表,将应力用弯矩的形式表达。弯矩的无因次形式为
(29)
(30)
可以导得
(31)
(32)
将上式联合最终得到构造正交异性板的应力表达形式
[zx(Mx-νyMy)λ2+zyνy(My-νxMx)]
(33)
[zxνx(Mx-νyMy)λ2+zy(My-νxMx)]
(34)

k4、k5经γ由各向同性板的弯曲要素表确定。
2.2 强度公式的分析
本文仅求得双向密加筋板最大应力值,而不考虑应力的分布。又在均布载荷作用下,正交异性板的最大应力值在其长边的中点,故仅用公式
[zx(Mx-νyMy)λ2+zyνy(My-νxMx)]
(35)
此时,要求L≥B。当L≤B时,可将L、B交换来计算结果。
3 有限元计算
3.1 有限元计算模型
板长取为定值L=1 800 mm,长宽比分别取0.8,1.0,1.2,1.4,1.6,1.8,2.2,2.4;
加筋类型及尺寸为
L60×40×4,L50×32×4,⊥4×60/4×40;
边界条件为沿周界刚性固定;
加筋数目(横筋×纵筋)为
3×3,3×4,3×4,4×4,4×5[4];
载荷为均布载荷,q=0.04 MPa。
3.2 计算数据分析
限于篇幅,表1给出加筋数为3×3,加筋尺寸为L60×40×4,板长为1 800 mm的双向密加筋板的计算结果。
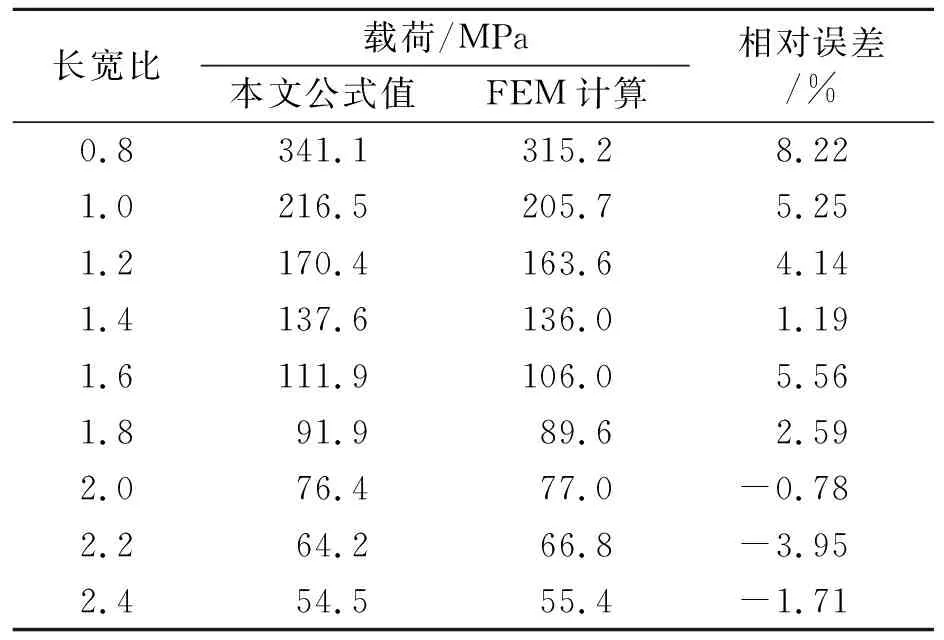
表1 最大公式值与FEM计算值比较(载荷)
图1包含了70个计算数据,显示出本文公式计算值与有限元计算结果之间相对误差的分布。其变异系数COV=1.29% 。
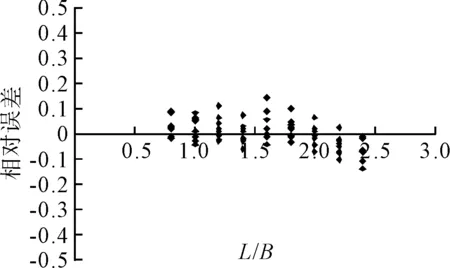
图1 本文公式与FEM计算结果的误差分布
3.3 计算挠度数据分析
构造正交异性板最大挠度为
(36)
式中k1通过γ由各向同性板的弯曲要素表确定。本文仅对长边为奇数筋的角钢通过使用1stopt软件对公式参数修正,得到
(37)
加筋数为3×5,加筋尺寸为L60×40×4,板长1 800 mm的双向密加筋板计算结果见表2。
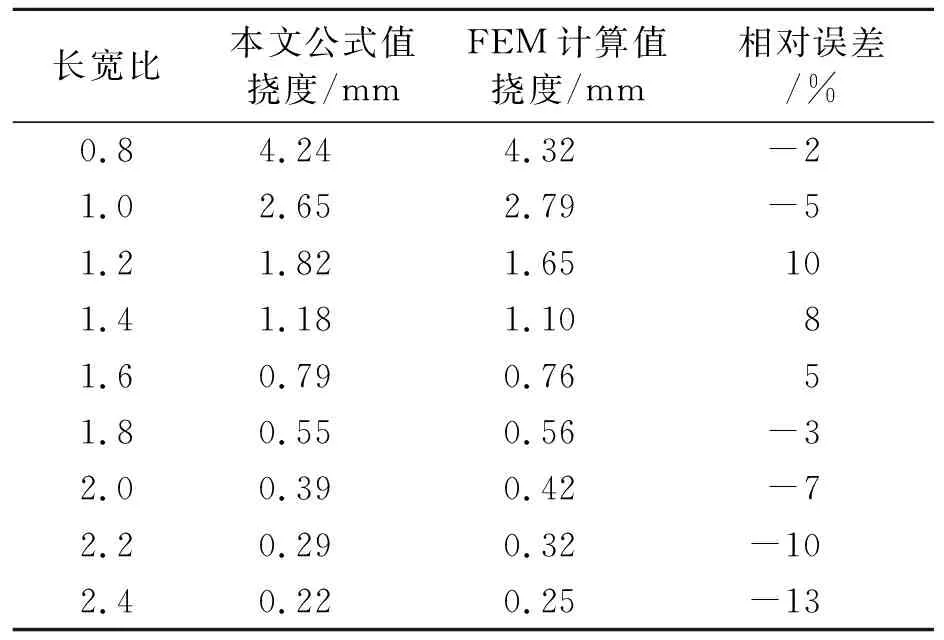
表2 最大公式值与FEM计算值比较(挠度)
4 强度公式的修正
相同尺寸的T型材、L型材仅一个方向的抗弯刚度相同,其抗扭刚度和另外方向的抗弯刚度是不一样的。故在有限元计算中,相同尺寸的T型材和L型材的应力值不一样,须对它们分别修正。又因本文所推导的公式需采用各向同性板的弯曲要素,而各向同性板的弯曲要素仅列出板两边中点的弯矩值。在均布荷重下四周刚性固定的各向同性板最大弯矩位于板长边的中点。故当长边加筋数为奇数时,其最大应力位置与最大弯矩位置相同;而当长边加筋数为偶数时,其最大应力位置与最大弯矩位置不同,也应分别修正。
通过对大量的有限元计算数据进行分析,综合考虑到以上因素以及误差的平均值、误差与边长比L/B的COV大小,利用最小二乘法,求得的修正系数见表3。
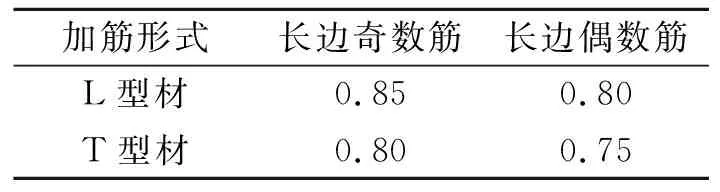
表3 公式修正系数
修正后的公式表达为
[zx(Mx-νyMy)λ2+zyνy(My-νxMx)]
(39)
式中:k——按表3所给数据选取。
5 结束语
大量计算验证了本文提供的修正公式能够对双向密加筋板的强度进行准确预报,公式形式简单,能够广泛运用于工程实际中。
[1] 刘彦峰,杨 平.密加筋板结构强度和稳定性的力学性能分析与结构设计[D].武汉:武汉理工大学,2006.
[2] PAIK J K, THAYAMBALLI A K, BONG J K. Large deflection orthotropic plate approach to develop ultimate strength formulations for stiffened panels under combined biaxial compression/tension and lateral pressure[J]. Thin-walled Structures, 2001(39):226-227.
[3] Я.И.考罗特金.板与圆筒形壳的弯曲及稳定性[M].陈铁,方译.北京:高等教育出版社,1958.
[4] 张征波.内河高速船的新型船体结构形式—双向加筋板船体结构[J].船舶工程,2004,26(1):22-25.
