The Magnetic Behavior of Fe Doped Into Hexagonal Boron Nitride Sheet
2012-01-19DENGXiaohui
DENG Xiao-hui
(Department of Physics and Electronic Information Science,Hengyang Normal University,Hengyang Hunan 421008,China)
0 Introduction
As possessing strange and interesting properties,the light element nanostructures,such as graphene,fullerene,carbon and boron nitrogen nanotubes,have been studied experimentally and theoretically[1-7].Hexagonal boron nitrogen sheet(h-BN)with sp2bond,consisting of III-and VIgroup elements may be implied in electronic devices in future.In contrast to the half-metal behavior of graphene,h-BN possesses polar B-N bond and wide band gap of 4.6eV,which promises the potential application of g-BN in this silicon age of the semiconductor.
Recently,the weak ferromagnetism in those compounds stimulated a research field of molecular magnets,which could be applied in high tempera-ture environment since metal magnets lost their ferromagnetic at high temperature.It is found that spin polarization could be induced by vacancy,impurity,and substitute in those systems.For example,Esquinazi et al.[8]detected a ferromagnetic signal from an oriented graphite that behaved quite differently from known magnetic impurities,suggesting an intrinsic origin of magnetism in graphene.Ma et al.[9]studied the magnetic properties of vacancies in graphite and carbon nanotubes.For graphite,the vacancy was spin polarized with a magnetic moment of 1.0.μBThe vacancy in carbon nanotubes could also induce magnetism,depending on their chiralities and structure configuration with respective to the tube axis.Wu el at.[10]found that carbon substitution in BN nanotubes can induce spontaneous magnetization.
For h-BN with d0ferromagnetism,has not been widely investigated except for some potential applications[10,12].Si et al.found the boron or carbon vacancy can induce an spontaneous splitting[13].For magnetic element doping,due to their intrinsic magnetization,may bring magnetic moment to nanostructures.When Fe is doped into h-BN,how is the magnetic behavior of Fe?In this paper,we focus on this topic.The density functional theory(DFT)calculations are applied to investigate electronic and magnetic properties on such systems.
1 Calculation method
Two cases,i.e.,Fe substitute nitrogen or baron atom named as SNand SB,are used.A 50atoms supercell is used to simulate 5×5pristine g-BN sheet.By randomly substituting a boron or nitrogen atom with Fe,the impurity systems SBand SNare constructed.Periodical boundary conditions are employed and adjacent layers are separated by a vacuum region 20Å.The DFT calculations are performed using a linear combination of atomic-orbital(LCAO)method[14]implemented in the SIESTA[15-16]code.For exchange correlation functional we choose the generalized gradient approximation(GGA)proposed by Perdew,Burke,and Ernzerhof.[17]The interaction between ions and electrons is described by the pseudopotential generated using Troullier and Martins scheme.[18]The double-zeta plus polarization atomic orbital basis set is employed in the calculation.The charge density project on real space grid and an equivalent plane wave cutoff energy of 500eV is used.a 5×5×1Monkhorst-Pack grid[19]is set for Brillouin zone sampling.The conjugate gradient minimization scheme[20]is used to perform atom position relaxation and cell optimization.The XCRYSDEN program[21]is adopted to calculate electronic spin density of state.
2 Results and discussion
The geometry structures of the pristine h-BN,SBand SNare fully optimized without any constrains upon them.Their initial structures are shown in figure 1.After relaxation,in the case of SB,lattice length a(or b)increases from 12.54Å to 12.80Å.With Fe substitute B,three adjacent N atoms expand outward because of the bigger atom radius of Fe comparing to the B and N.The final distances dFe-Nis 1.79Å.Atom site situations far from the dopant Fe remains almost unchanged comparing with the pristine h-BN.The dB-Nis 1.46 Åand that in pristine g-BN is 1.45Å.For the case of SN,the local symmetry of pristine g-BN is broken after Fe doping.Three dFe-Nare 1.74Å,1.76 Å.and 1.76Å,respectively.The Fe-N distances in case of SBare larger than the Fe-B distances in case of SN.We point out our B-N distance of pristine g-BN is 1.45Å,according to that reported by Si et al.[13].

figure 1 The structures for h-BN sheet.The a and b sites indicate the SNand SBcases,respectively.
In order to investigate magnetic properties induced by Fe substituting B or N.The electronic density of states(DOS)is calculated.The obtained DOS near Fermi energy(Ef)are shown in figure 2(b)and(c).For comparison,that for the pristine h-BN also is shown in figure 2(a).It can be found that the ground state of pristine h-BN is non-spin-polarized then the magnetic moment is zero.But for the sake of Fe doping,the pristine h-BN spin polarize.In the case of SB,near the Ef,majority DOS is different from minority DOS.A significant peak occupied by majority spin electrons and minority spin peak weaken.The half-metallic behavior is also found.The majority spin component posseses a band gap while the minority spin component is metallic.Such half-metallic behavior also were found in other doped system[13,22,23].Therefore,the SBcase is expected to have a big magnetic moment.But in SNcase,spin-polarization behavior is not obvious.Minority DOS only shift forward compared with Majority DOS near Ef.

Figure 2 The total majority and minority DOS and PDOS of Fe 3dorbitals(solid and dash lines,respectively)of(a)pristine g-BN,(b)the SBcase,and(c)the SN case.The Fermi energy is set to zero by a dot line.
To understand the influence of the Fe dopant on magnetism,here we analysis the interaction be-tween the orbital of the Fe and the h-BN from the calculated DOS.In figure 2(b)and figure 2(c)we also present the contribution of 3dpartial density of states(PDOS)of Fe atom to compare with the total DOS.The picture shows that the energy of Fe 3dmainly concentrates near the Ef,And the total DOS near Fermi energy level are mainly governed by Fe 3dstates.The minority spin of Fe 3d states move right relative to that of the majority,indicating the spin polarized splitting near the Efin both cases.From figure 2,we also found that proportion of Fe 3dstates to total DOS in SBis relatively lower however that in SNis relatively higher.So we conclude that the contribution of other atoms or orbitals on magnetism in SBis rather than that in SN.The quantity analysis will be carry out in the following part to make clear this point.
The total magnetic moment of the SBis 5.0μB.The magnetic moment mainly comes from Fe and three adjacent N atoms.Fe donates 3.953μBand every N atom 0.219μB.For main donator Fe atom,from standard Mulliken population analysis,we find that spin polarization mainly comes from its 3d orbital with value of 3.529μB.The s orbital of Fe atom donates 0.207μB.For the case of SN,the total magnetic moment is 1.0μB.As the same as SBcase,the spin density also comes from Fe atom.But for three adjacent B atoms,electronics is almost non-spin-polarized.The other magnetic moment come from six adjacent N atom polarized directly by Fe atom.

Table 1 Magnetic moments M(inμB)and occupied electrons numbers of Fe atom in substituted h-BN and in bulk Fe(BCC)from the standard Mulliken population analysis.Ppindicates polarized orbital.↑and↓indicate spin up and spin down.
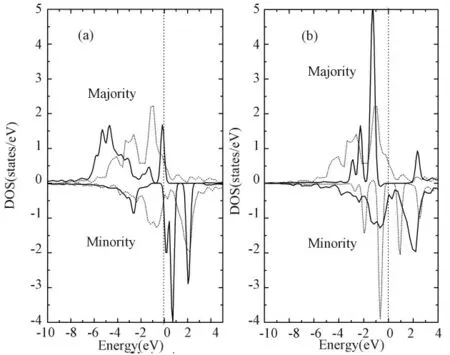
Figure 3 The total DOS of Fe atom in(a)the SBcase and(b)the SNcase(solid lines).Those in BCC bulk Fe are plotted in short dot lines.The Fermi energy level is denoted by dot lines.
The magnetic moments in the SBand SNare 5.0and 1.0μB,respectively.As we know,the magnetic moment of bulk Fe(BCC lattice)is~2.2μB.According to discussion above,the magnetic moments in SBand SNcome from 3dstates of Fe atom.How does the valence electron of Fe atom in substituted h-BN system behave?To explain this point,we list the occupied electronic charges and magnetic moments of Fe atom in substituted h-BN system from Mulliken population analysis in table 1.For comparison,the obtained occupied electronic charges in bulk Fe are also listed.On the SBcase,the magnetic moment of Fe atom is 3.953μB,which is larger than that in bulk Fe.The spin up(down)electrons in SBincreases(decrease)compared with bulk Fe.The two aspects result in that the magnetic moment increases from 2.352μBto 3.953μB.This feature also can be found from the total DOS of Fe atom in SBand in bulk Fe(seen from figure 3(a)).The total DOS of spin up electron of Fe atom broaden and the electron numbers occupied Fermi energy increase.A significant occupied minority spin peak vanishes.On the SNcase,the magnetic moment of Fe atom is 1.324μB,which is smaller than that in bulk Fe.The spin up(down)electrons in SNdecrease(increases)compared with bulk Fe(listed in table 1).The majority and minority spin DOS contract(figure 3(b)).The Fermi energy level has no occupied electron-ics.The minority spin DOS exceed the majority spin DOS by a small energy value indicating Fe atom in this system is not completely spin-polarization.
3 Conclusion
In summary,we have performed spin polarization calculations under the DFT to investigate the magnetic behavior of Fe atom doped into the h-BN sheet.We find that a nitrogen or boron atom substituted by Fe can induce magnetism.The total magnetic moments in SNand SBare 1.0μBand 5.0μB,respectively.A half-metallic behavior is found in the SBcase.The magnetic moment is mainly dominated by Fe 3dstates from standard Mulliken population analysis.The magnetic behavior of Fe in h-BN is interesting.In SNcase,the spin up electrons in SBincreases compared with bulk Fe,however,the spin down electrons decreases.Just two reasons result in the magnetic moment of h-BN.The situation is the opposite for SN.
[1]Wong S S,Joselevich E,Woolley A T,et al.Covalently functionalized nanotubes as nanometre-sized probes in Chemistry and Biology[J].Nature,1998,394:52-55.
[2]Ajayan P M.Nanotubes from carbon[J].Chem.Rev.,1999,99:1787-1800.
[3]Banhart F.Irradiation effects in carbon nanostructures[J].Rep.Prog.Phys,1999,62:1181.
[4]Bochrath M,Liang W L,Bozovic D,et al.Resonant electron scattering by defects in single-walled carbon nanotubes[J].Science,2001,291:283-285.
[5]Novoselov K S,Geim A K,Morozov S V,et al.Electric field effect in atomically thin carbon films[J].Science,2004,306:666-669.
[6]Ouyang M,Huang J L,Cheung C L et al.Atomically resolved single-walled carbon nanotube intramolecular junctions[J].Science,2011,291:97-100.
[7]Woodside M T,Mceuen P L.Scanned probe imaging of single-electron charge states in nanotube quantum dots[J].Science,2002,296:1098:1101.
[8]Esquinazi P,Setzer A,Hohne R,et al.Ferromagnetism in oriented graphite samples[J].Phys.Rev.B,2002,66:024429-024438.
[9]Ma Y,Lehtinen P O,Foster A S,et al.Magnetic properties of vacancies in graphene and single-walled carbon nanotubes[J].New J.Phys,2004,6:68.
[10]Wu R Q,Liu L,Peng G W,et al.Magnetism in BN nanotubes induced by carbon doping[J].Appl.Phys.Lett.,2005,86-122510-112512.
[11]Deng X H,Zhang D Y,Si M S,et al.The improvement of the adsorption abilities of some gas molecules on g-BN sheet by ccarbon doping[J].Physica E,2011,44:495-500.
[12]Schmidt T M.,Baierle R J,Piquini P,et al.Theoretical study of native defects in BN nanotubes[J].Phys Rev.B,2003,67:113407-113410.
[13]Si M S,Xue D S.Magnetic properties of vacancies in a graphitic boron nitride sheet by first-principles pseudopotential calculations[J].Phys.Rev.B,2007,75:193409-193412.
[14]E.Artacho,D.Sanchez-Portal,P.Ordejon,et al.Linear-Scaling ab-initio calculations for large and complex systems[J].Phys.Status Solidi B,1999,215:809-817.
[15]J.M.Soler,E.Artacho,J.D.Gale,et al.The SIESTA method for ab initio order-N materials simulation[J].J.Phys.:Condens.Matter,2002,14:2745.
[16]P.Ordejon,E.Artacho,J.M.Soler.Self-consistent order-N density-functional calculations for very large systems[J].Phys Rev.B,1996,53:R10441-R10444.
[17]J.P.Perdew,K.Burke,M.Ernzerhof.Generalized gradient approximation made simple[J].Phys.Rev.Lett.,1996,77:3865-3868.
[18]N.Troullier,J.L.Martins.Efficient Pseudopotentials for plane-wave calculations[J].Phys Rev.B,1991,43:1993-2006.
[19]Monkhorst J,Pack J D,Special points for brillouinzone Integrations[J].Phys.Rev.B,1976,13:5188-5192.
[20]D.M.Bylander,L.Kleinman,S.Lee.Self-consistent calculations of the energy bands and bonding properties of B12C3[J].Phys Rev.B,1990,42:1394-1403.
[21]A.Kohalj.Computer graphics and graphical user interfaces as tools in simulations of matter at the atomic scale[J].Comput.Mater.Sci.,2003,28:155-168.
[22]L.H.Ye,A.J.Freeman,B.Delley.Half-metallic ferromagnetism in Cu-doped ZnO:density functional calculations[J].Phys Rev.B,2006,73:033203-033206.
[23]M.S.Si,D.S.Xue.First-principles study of silicondoped(5,5)BN nanotubes[J].Europhys.Lett,2006,76:664.
杂志排行
衡阳师范学院学报的其它文章
- Oscillation for the Solutions of Hyperbolic Partial Differential Equation with Damped Terms and High order Laplace Operator
- EmployingMixed Ligands to Construct 3d-4f Framework:Hydrothermal Synthesis,Structure and Magnetic Properties
- Application of Materialized View as Aggregate Table in Data Warehouse
