关节式坐标测量机结构参数标定优化采样策略

奚 思，于连栋

(合肥工业大学仪器仪表学院，安徽合肥 230009)

关节式坐标测量机结构参数标定优化采样策略

奚 思，于连栋

(合肥工业大学仪器仪表学院，安徽合肥 230009)

利用高斯—牛顿法求解便携关节式坐标测量机的标定参数时，其参数的可辨识性与Jacobin矩阵的条件数有关，而Jacobin矩阵的条件数决定于标定采样点的坐标。因此，必须对参数标定的采样策略进行优化。文中以锥孔标准杆件标定法为例，提出一种优化的采样策略来增大各个关节取值范围，从而使条件数最小化。经实验验证，采用这种优化采样策略标定提高了测量系统的精度。

参数标定;采样策略;高斯—牛顿法;条件数

便携关节式坐标测量机具有灵活、便携、价格较低等优点，适宜于车间现场使用，因此发展迅速、应用广泛，其测量功能及测量精度已达到传统三坐标测量机中等精度水平［1］。便携式坐标测量机是一种串联开链结构，因此其误差因素复杂:第一，由于其机械结构串联导致各个关节的角度误差，通过杆件的长度被逐级放大;第二，加工及装配过程中难保证各个结构参数与测量机设计初始值一致。因此难以保证测量机的测量精度。由于便携关节式坐标测量机具有多个自由度，且其在应用中有便携的需求，导致其无法固定于特定的位置姿态，以便直观地检定各单项结构参数误差。因此，主要还是通过标定的方法获得关节式坐标测量机的结构参数，以便得到精确的测量方程，从而提高测量机的精度。

目前的便携式测量机结构参数标定方法，对标定过程中采样策略并未做具体研究，如标准杆件法，石英棒在空间放置位置具有一定的随机性。为得到理想的标定结果，只能无谓地增加标定次数。文中以标准杆件法为例，通过研究高斯—牛顿矩阵性态问题得出条件数对参数辨识性的影响，并通过模拟实验找出了采样点的各关节角度范围与条件数的关系，以此提出一种优化的采样策略。

1 标定过程中参数可辨识性

用D－H方法推出的测量机测量方程式中包含21项待辨识的参数:杆件长度 l1、l2、l3、l4、l5;杆件扭角α1、α2、α3、α4、α5;关节转角 θ2、θ3、θ4、θ5、θ6;杆件偏置量 d2、d3、d4、d5、d6;测头偏置量 l6，21 项参数记为 b1，b2，…，b21。对于可观测性的量 x 与 y 有［2］?

式中，x 是自变量;y 为变量，向量 b=(b1，b2，…，bn)为n维待辨识的参数，n=21。要标定出这21项参数，则要通过m(m＞n)组观测数据(x1，y1)…(xm，ym)寻求参数向量b的最佳估计值，这是典型的参数辨识问题。向量b的最佳估计值就是使得残差 r=yi－fi，i=1，…，m 最小。于是有目标函数［3－4］

采用高斯—牛顿法将上式的非线性问题转化为线性问题得线性方程

式中，A为 m ×21(m ＞21)阶 Jacobin矩阵;Δ=［Δ1，Δ2，…，Δ21］T为21项待辨识的结构误差参数增量。可看出Jacobin矩阵A与残差r直接决定了方程组的解;矩阵A的性态决定了方程组解对干扰的敏感性，残差r的大小取决于参数初值的选取以及测量机系统的稳定性等因素。

对于线性方程组Ax=b，关于矩阵性态有如不等式［5］

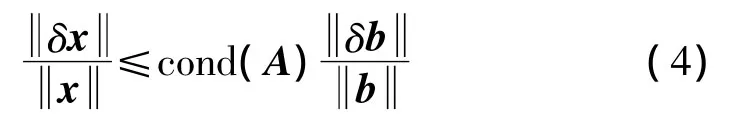
2 模拟实验

在实际进行便携式坐标测量机的参数标定时，采样点坐标决定Jacobin矩阵的条件数。这里做个模拟实验，采用基于两点距离的高斯—牛顿法对测量机参数辨识，给出两组柔性坐标测量机的关节空间坐标值A组和B组，其中A组数据各个关节变化范围大，B组数据则将各个关节坐标值变化控制在很小的范围内。将21项误差初始值取相同值，发现用A组数据计算得出的Jacobin矩阵的条件数量级在103，用B组数据计算得出的Jacobin矩阵的条件数量级在106，由此可见在柔性坐标测量机的实际应用中，能够通过增大测量机各关节空间的取值范围来有效的改善Jacobin矩阵的条件数。

3 优化采样策略

锥孔标准杆件标定法是分别记录下探测锥孔标准杆两端时关节式坐标测量机的姿态，并以两端锥孔时球心之间的距离作为基准量来逆解测量机的21项参数［6］。

根据以上理论研究及模拟实验的结论，为增大采样的各个关节的变化范围提出一种采样策略:将标准件在测量机测量范围内均匀放置，并在每一个位置采样时均匀旋转锥窝标准杆，可有效增大各个关节的取值范围。为验证这一策略的有效性，分别对比一下3种采样策略。

(1)A组实验将标准杆基座固定在与坐标机同一平面上，距离a=40 cm处，固定石英棒采样500组数据，如图1所示。处理所得结构参数如表1所示。

图1 锥孔标定示意图

(2)B组实验将标准杆件基座固定在与坐标机同一平面上，距离同样为40 cm处在空间内均匀旋转石英棒采样500组数据，处理所得结构参数如表2所示。

具体采样方法如图2所示。图中粗直线为两头带锥孔的石英棒，即标准杆件。在标定时，将石英棒在不同平面内均匀旋转采样，例如每隔10°放置标准杆并采样，同可得到36组比对结果，接着，依次在平面2、平面3、…、平面n内均匀采样，一直延续到整个测量空间［7］。

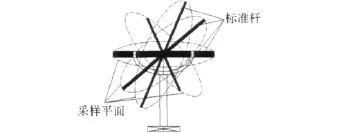
图2 石英棒示意图

(3)C组实验将标准杆件基座固定在与坐标机同一平面，保持测量机位置固定不动，标准杆件以测量机底座为圆心，40 cm为半径旋转，如图3所示，每隔60°放置一个位置采样500组数据，采样时石英棒的旋转类似于步骤(2)。处理所得结构参数如表3所示。

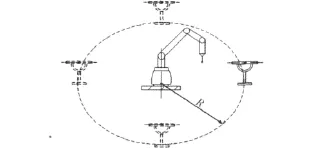
图3 石英棒围绕测量机旋转方式

表1 A组标定所得参数

表2 B组标定所得参数

表3 C组标定所得参数

将所求得的3组参数带入坐标测量机，并对300 mm的量块进行50次测量，量块摆放位置任意选定。测量数据处理结果如表4所示。由表4可得C组中在保证标准杆件基座与坐标测量机距离与采样次数均相同的情况下，空间内尽量均匀旋转整个标准件和石英棒这种采样策略标定得来的结果，相比另外两种采样策略要好得多，所得参数带入测量机后，测量值更加接近真实值。

表4 3组参数标定结果

4 结束语

针对便携式坐标测量机参数标定过程中运用高斯—牛顿法时矩阵性态的问题，指出了在标定柔性坐标测量机21项结构参数时，应减小Jacobin矩阵的条件数。为减小Jacobin矩阵的条件数，提出了一种增大各个关节取值范围的采样策略。以锥孔标准杆标定法为例，将标准件在测量机测量范围内均匀放置，并在每一个位置采样时均匀旋转锥窝标准杆，有效增大了各关节的取值范围。最后通过精度对比试验验证了这一策略增强了测量机参数系统误差的可辨识性，保证了便携式坐标测量机的精度。

［1］于连栋，程文涛，费业泰.基于激光跟踪仪的关节式坐标测量机参数标定［J］.中国科学技术大学学报，2009，39(12):1329－1332.

［2］程文涛.关节式坐标测量机标定技术研究［D］.合肥:合肥工业大学，2011.

［3］BAI YING，WANG DALI.On the comparison of interpolation techniques for robotics position compensation［C］.IEEE International Conference on Robotics ＆ Automation，2003:3384－3389.

［4］邓乃扬.无约束最优化计算方法［M］.北京:科学出版社，1982.

［5］陈志平，徐成贤.不精确高斯－牛顿法的收敛性［J］.工程数学学报，1997，14(4):1 －7.

［6］郑大腾.柔性坐标测量机空间误差模型及最佳测量区研究［D］.合肥:合肥工业大学，2010.

［7］汪平平.柔性坐标测量机精度理论及应用技术研究［D］.合肥:合肥工业大学，2006.

An Optimized Sampling Strategy of the Parameters Calibration for PCMM

XI Si，YU Liandong
(School of Instrumentation，Hefei University，Hefei 230009，China)

We use the Gauss-Newton method to find the parameters in the parameters calibration for PCMM(Portable Coordinate Measuring Machine).Then we find the relationship between the identification of parameters and the conditions numbers of Jacobin Matrix，and in practical the conditions numbers of Jacobin Matrix depends on the sample point.Therefore，the sampling strategy must be optimized.Using the cone and standard bar as a calibration standard，this paper presents an optimized sampling strategy to increase the value range of each joint and thus minimize the conditions number of Jacobin Matrix.Experiment results show that the sampling strategy of calibration greatly improves the measurement accuracy.

parameters calibration;sampling strategy;Gauss-Newton;the conditions numbers

TP274+.2

A

1007－7820(2012)08－132－03

2012-02-28

国家自然科学基金资助项目(51075117)

奚思(1988—)，女，硕士研究生。研究方向:精密仪器及机械。