机载雷达坐标转换及数据处理的建模与仿真

徐晚成，王 刚

(西安电子科技大学电子工程学院，陕西西安 710071)

机载雷达坐标转换及数据处理的建模与仿真

徐晚成，王 刚

(西安电子科技大学电子工程学院，陕西西安 710071)

通过对雷达常用坐标和数据处理的基本理论介绍，给出了机载雷达坐标转换和数据处理的算法，以算法为基础建立了仿真模型，给出了具体的仿真流程。仿真结果表明，坐标转换的算法精度达到了要求，数据处理能够完成对目标的稳定跟踪。

坐标转换;雷达数据处理;快速数据关联;扩展卡尔曼滤波

坐标转换是雷达数据预处理的重要组成部分，其精度直接影响后续处理的复杂程度和准确性。对雷达测量数据进行处理，可以有效地抑制测量过程中引入的随机误差，精确估计目标位置和有关的运动参数，预测目标下一时刻的位置，并形成稳定的目标航迹［1］。随着雷达体制的发展，相控阵雷达的数据处理系统，能够为相控阵雷达资源调度及天线波束指向提供依据，还可以为目标的识别和目标的拦截等提供条件。

1 坐标转换

在雷达跟踪系统中，目标量测所在的坐标系与数据处理所在的坐标系通常不一致。此时，需通过坐标转换技术，将所有数据信息格式统一到同一坐标系中。

1.1 坐标系之间的转换公式

(1)地理坐标系和大地直角坐标系之间的转换［1］。如图1所示。地理坐标系的原点选择在地球球心，Zg轴定义为地球的自旋轴，正向为从地球球心指向北极;Xg轴定义在赤道平面上，从地球球心指向格林尼治子午线的轴线;Yg轴由Xg轴和Zg轴确定，构成一个右手直角坐标系。大地直角坐标系的各个坐标轴定义与地理坐标系的坐标轴定义完全相同。但目标的位置表示是由目标在各个坐标轴上的投影位置来表示。

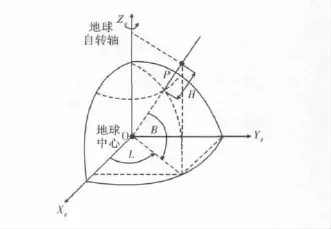
图1 地理坐标系和大地直角坐标系

目标点P在地理坐标系中的坐标可表示为(L，B，H)，L为大地经度，B为大地纬度，H为大地高。目标点P在大地直角坐标系中的坐标位置为(x，y，z)，则目标在地理坐标系和大地直角坐标系之间的位置变换关系为

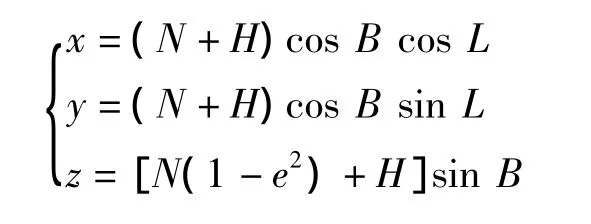
反变换为

其中，N为椭球的卯酉圈的曲率半径;e为椭球的第一偏心率。假设a、b分别为椭球的长短半轴。

(2)NED坐标系与地理坐标系之间的转换。如图2所示。NED坐标系的原点定义在载体的质心;N轴为地理指北针方向(北);E轴为地球自转切线方向(东);D轴为载体质心指向地球球心的方向。图中所示L为载机原点所在的经度;B为载机原点所在的纬度;H为载机原点的海拔;A为大地方位角。

图2 NED坐标系与地理坐标系

根据上述过程，可以得到以下两个旋转公式

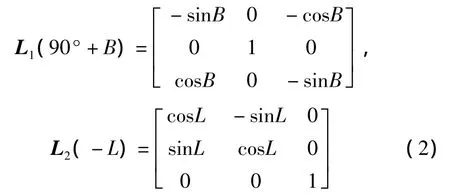
假设目标在NED坐标系中的坐标为N;在大地直角坐标系中的坐标为Xg;X为载机在大地之交坐标系中的位置。则两者间的转换关系为:Xg=L2(－L)L1(90°+B)N+X。再根据式(1)将(xg，yg，zg)转换为(L，B，H)，就最终完成了转换。

(3)NED坐标系(载机地理坐标系)与载机坐标系之间的转换。如图3(a)，图3(b)所示，载机直角坐标系的原点定义在载机的质心上。Xd轴定义为载机纵轴，正向定义为指向机头方向;Yd定义为由原点指向右机翼;Zd轴由Xd轴和Yd轴确定，构成右手坐标系，正向定义为由载机质心指向载机下方。

如图3(c)，图3(d)所示。假设载机横摇的角度为R，纵摇的角度为P，载机的航向和正北方向之间的角度为an。

图3 载机直角坐标系和NED坐标系的转换关系

根据坐标旋转的基本公式，可以得到以下3个基本旋转矩阵

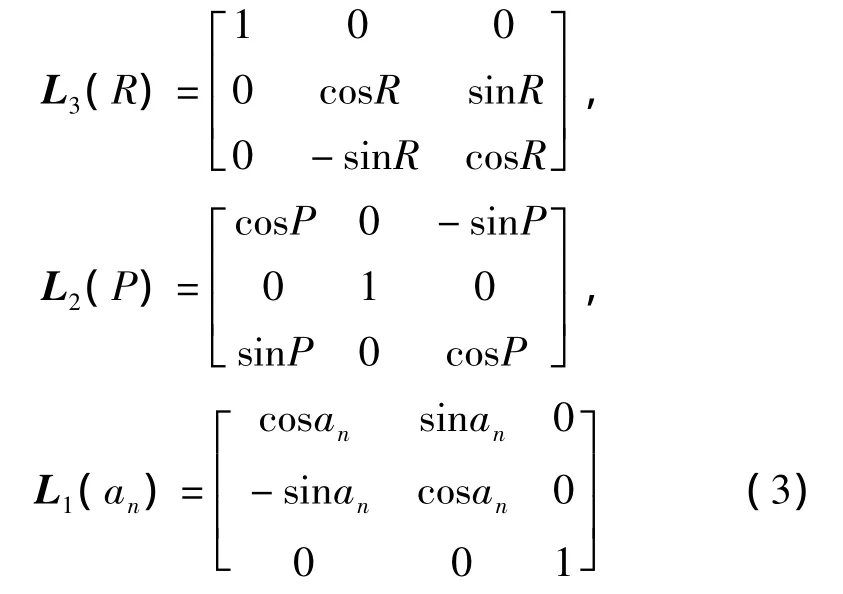
则根据上面3个矩阵，可以得到坐标变换矩阵为L=L3(R)·L2(P)·L1(an)。若需要从载机坐标系转换为 NED 坐标系，L'=L－1。

1.2 坐标系转换仿真

坐标系之间的转换过程如图4所示。

图4 坐标系之间的转换流程

由图4可知，4种坐标系之间可以相互转换。其中较容易发生误差的是大地直角坐标系到地理坐标系的转换。由于大地维度B和大地高H之间的相互制约关系，很难直接求得。所以在仿真中采用迭代法［3］求解，可以到达较高的精度。

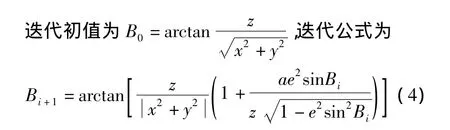
2 雷达数据处理

数据处理是对信号处理得到的点迹报告进行后期处理，以完成以下几个基本功能:(1)建立目标航迹，并进行航迹管理。(2)检测点迹与航迹的配对，即航迹关联。(3)目标的跟踪滤波及预测。

2.1 航迹起始和航迹终结算法

航迹的确认采用m/n滑窗准则，即如果在n次观测中，该目标航迹关联配对成功次数≥m，则判定该航迹确认成功，否则撤销该暂时航迹。通常可以设定航迹确认 m/n准则为 m=2，n=3，为正常航迹起始［1］。目标航迹终止采用了序列概率比检验(SPRT)算法［2］，具体算法如下

定义参数

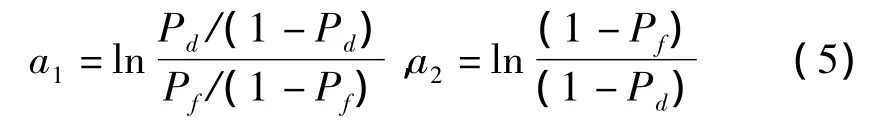
其中，Pd和Pf分别为检测概率和虚警概率。定义检验统计变量ST(k)为:ST(k)=ma1其中m为检测数，定义k时刻航迹撤销门限Tc(k)=lnc1+ka2，其中c1=β/1－α，α为漏撤概率，β为误撤概率。航迹终止决策逻辑可以表示为ST(k)＜Tc(k)，航迹撤销，否则航迹维持。

2.2 航迹关联算法

航迹关联算法［2］包括最近邻法(NNP)，概率数据互联法(PDAF)，联合概率数据互联法(JPDA)等。其中PDAF是一种实时性较好的关联算法。该算法计算量小，性能优于最邻近法。但其跟踪性能在回波密集时不太理想。JPDA则被认为是解决密集回波下多目标数据关联有效算法之一，其目标跟踪成功率在各种环境下都很高。但其计算量在目标和回波密集时呈“组合爆炸”的趋势，在实际工程中难以广泛应用。

快速数据关联滤波(Fast Data Association Filter，FDAF)算法重点对关联门相交区域中的公共回波进行分析，并综合考虑了关联门内其余候选回波对目标航迹更新的影响。以较小的计算代价得出与联合概率数据互联法(JPDAF)接近的关联概率，能够有效地降低密集回波下多目标数据关联计算的复杂性，并维持一定的跟踪性能。具体算法步骤见文献［2］。

2.3 跟踪滤波算法

对于弹道目标，通常采用常加速度模型(CA)来描述其运动状态，且采用扩展卡尔曼(EKF)滤波模型来完成跟踪。具体的算法步骤见文献［4］。

2.4 雷达数据处理仿真流程

根据雷达工作的模式，建立航迹头、暂时航迹和稳定航迹3种航迹表，其内都存储有航迹的距离、方位和俯仰角度信息;暂时航迹表另外含有威胁程度、起始逻辑滑窗、估计速度、预测下一位置以及预测误差信息;稳定航迹列表另外含有SPRT算法参数、航迹号、估计速度和加速度信息，另外定义结构体存储稳定航迹的EKF参数信息。并设定最多同时跟踪16条稳定航迹，如探测到多于16条的稳定航迹，则根据目标的威胁程度排序，跟踪威胁程度较高的前16个目标。

在仿真起始时，第一次接收到的自由点迹都起始为航迹头，然后与第二次接收到的点迹信息进行关联，形成一系列暂时航迹，并预测目标下一位置，形成关联门，并更新起始逻辑滑窗内容;没有关联上的点迹则起始为新的航迹头。第三次接收到的点迹信息先于暂时航迹进行关联，关联成功则判断起始逻辑滑窗内容是否满足起始条件，满足则转为稳定航迹，存入稳定航迹列表，分配航迹号，并建立Kalman滤波。剩余点迹与航迹头进行关联判断是否形成暂时航迹，重复以上过程直至建立稳定航迹为止，之后便如图所示的处理过程进行。稳定航迹的关联门为使用Kalman滤波参数定义的椭球门。整体仿真工作流程如图5所示。

3 仿真结果与分析

3.1 坐标转换精度分析

容易出现误差的部分为大地直角坐标系与地理坐标系的转换，设目标地理坐标为:L=140°，B=0.0231°，H=2 000 m，X= －4 887 468.101 099，Y=4 101 072.681 023，Z=2 553.535 807。a=6 378 137.0，b=6 356 752.314 1。表1为采用迭代法的次数与结果以及采用直接法的比较。

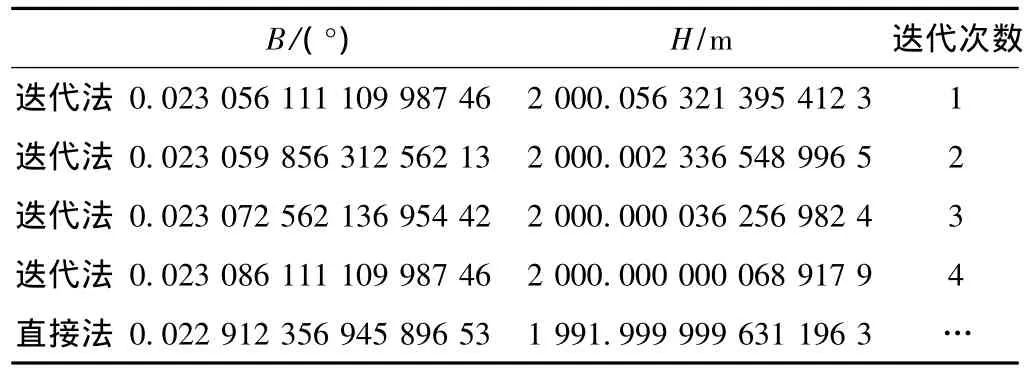
表1 大地直角坐标系与地理坐标系的转换的迭代次数比较

如表1所示，采用迭代法的坐标转换算法明显要精确于直接法的算法，且一般4次迭代就可达到较高的精度。

3.2 数据处理

在VS2005环境下以C++语言编写实现的雷达数据处理模块，仿真共设置4个目标，起始距离分别为6 000 km，15 000 km，25 000 km，40 000 km。在多目标跟踪模式下对目标进行跟踪。

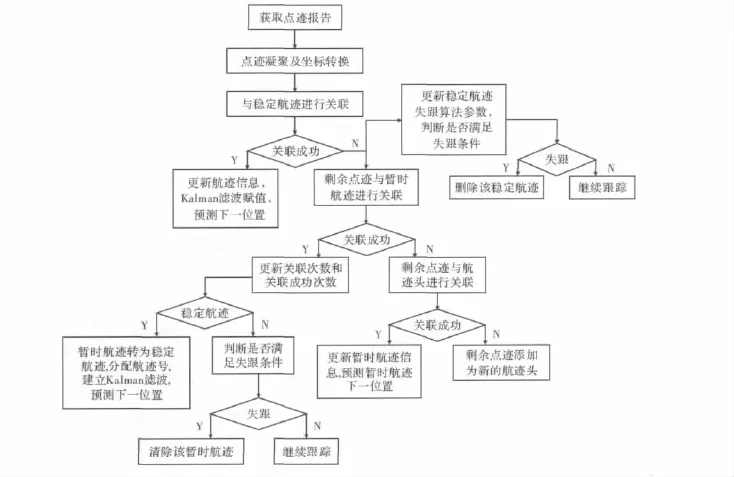
图5 数据处理流程

图6所示为调用数据处理模块两次后的界面显示图。其中共起始了6条暂时航迹，在第3次调用数据处理模块后，结果界面如图7所示，可见6条暂时航迹中有4条成功转为稳定航迹开始跟踪，剩余两条错误跟踪的暂时航迹保持跟踪判断的状态，继续存储在暂时航迹列表中。在继续调用跟踪中，数据处理模块能够稳定地跟踪这4个目标。

图6 调用数据处理模块后的界面显示

4 结束语

文中介绍了机载雷达常用坐标系的基本定义和转换关系，以及雷达数据处理的关联算法、滤波算法及航迹起始终结算法，设计了坐标转换与数据处理的仿真模型和仿真流程，通过编程仿真，坐标转换模块得到了较高的精度，数据处理模块也能够在有杂波剩余和干扰的情况下完成对目标航迹的确立和稳定跟踪。

图7 调用数据处理模块后的界面显示

［1］何友，修建娟，张晶炜，等.雷达数据处理及应用［M］.北京:电子工业出版社，2009.

［2］王雪松，肖顺平，冯德军.现代雷达电子战系统建模与仿真［M］.北京:电子工业出版社，2010.

［3］崔永俊.空间直角坐标系与大地坐标之间的变换方法研究［J］.华北工学院学报，2003(24):463－465.

［4］杨万海.雷达系统建模与仿真［M］.西安:西安电子科技大学出版社，2007.

［5］欧阳文，何友，斩煜.机载火控雷达训练模拟器的设计［J］.计算机仿真，2006(1):261 －265.

［6］张宏伟，张树平.基于起伏RCS模型的机载PD雷达相干视频杂波模拟［J］.电子科技，2007(3):47－51.

Modeling and Simulation of Coordinates Transform and Data Processing for Airborne Radar

XU Wancheng，WANG Gang
(School of Electronic Engineering，Xidian University，Xi'an 710071，China)

According to the basic theory of coordinates transform and data processing of radar，this paper introduces the detailed algorithms，and also gives the simulation model and specific simulation process based on those algorithms.Results show that the coordinates transform algorithms can achieve the required accuracy and the data processing can track targets stability.

coordinates transform;radar data processing;FDAF;EKF

TN957

A

1007－7820(2012)06－067－04

2011-12-31

徐晚成(1987—)，女，硕士研究生。研究方向:系统建模与仿真。王刚(1987—)，男，硕士研究生。研究方向:雷达对抗。