Singer模型在周跳探测中的应用

卢 超，卢艳娥，刘少鹏

（空军工程大学 电讯工程学院，陕西 西安 710077）

在高精度GPS数据处理中，由接收机所获得的载波相位是用于估计参数的主要观测量。在接收机进行连续的测量过程中，由于某种原因而导致整周计数发生错误，就会使相位测量值较之正常值出现一个整数周的跳跃，但不足一周的部分仍然正常，该跳跃被称为周跳。

对周跳进行处理，首先需要确定载波相位观测值的时间序列中所发生周跳的位置，即周跳检测。笔者介绍一种在Singer模型和kalman滤波基础上利用多项式探测周跳的方法。

1 kalman滤波的过程

1.1 载波相位模型

针对单频载波相位和码伪距测数值的情况，载波相位可表示为[1]：

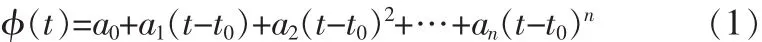
其中 t为观测历元时刻；a0、a1、a2…an为待定系数，t0为时间基准。

为了简化模型，设φ（t）服从二次分布，同时考虑噪声误差 w（t），w（t）为零均值高斯白噪声，则有：

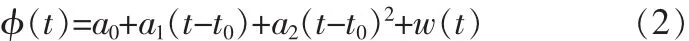
1.2 kalman滤波算法原理

在用卡尔曼滤波算法时，关键是确定状态向量、建立系统方程、量测方程和确定噪声统计特性等。

系统的状态向量：代估计量假设为singer模型，通过白噪声化，驱动噪声可以表示成Markov过程，即：

其中 w（t）是白噪声，并满足：

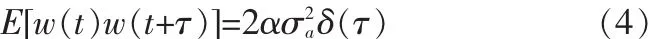
系统状态向量选取为：

则系统噪声向量为：

1.3 系统方程的推导

根据系统的误差状态向量、系统噪声向量和数学模型，得到的系统方程如下：

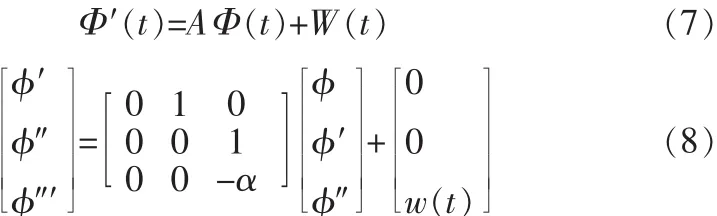
由离散时间系统与连续时间系统之间的关系，我们得到离散时间系统的状态方程为[2]：

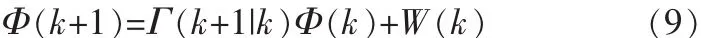
其中

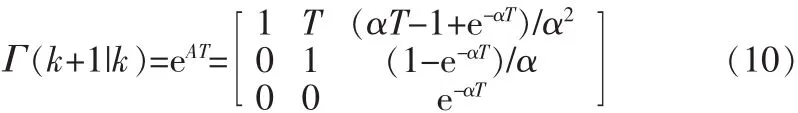
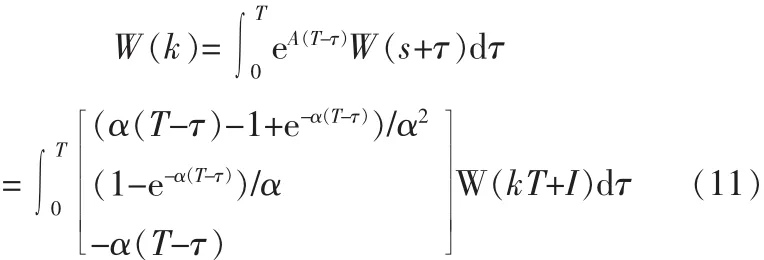
可以得到相应的W（k）的协方差矩阵：

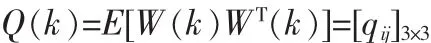
其中

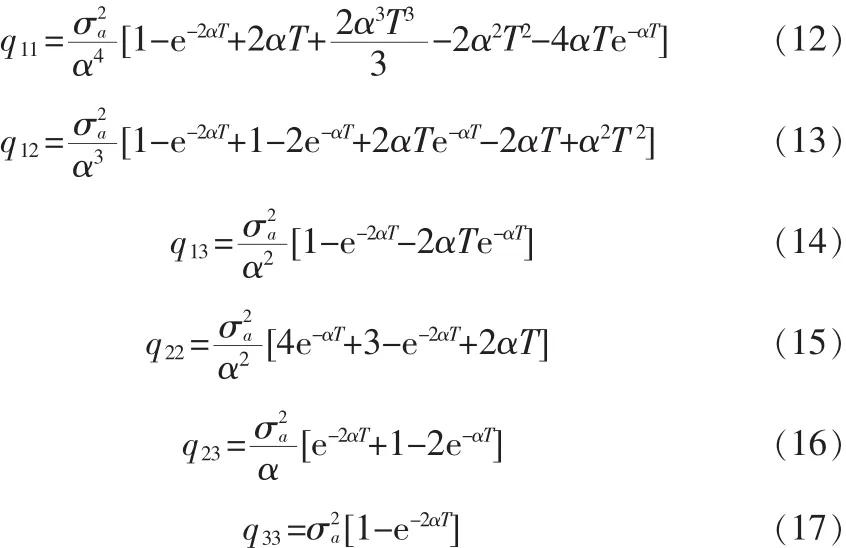
1.4 量测方程的推导

量测方程矩阵可以把观测量和状态向量联系起来。利用单频载波相位，由观测方程[3]（为多普勒频率），和载波相位观测方程求导（λ为载波波长，N为模糊度，δρI为电离层折射群延迟）、基本测距[4]公式可得：

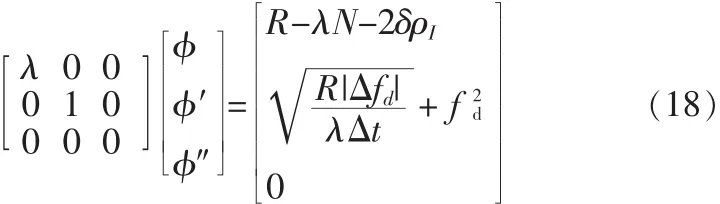
其中

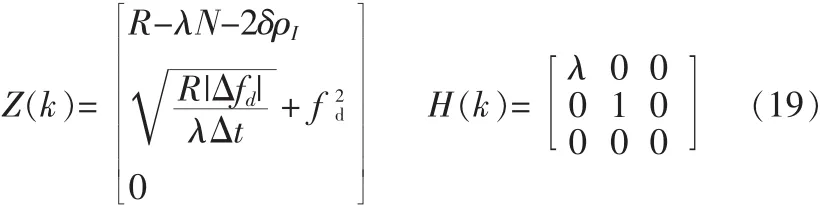
得到系统量测方程为：

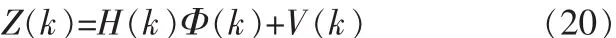
系统噪声和量测噪声是互不相关的零均值高斯白噪声序列。量测噪声方差阵V的对角线元素σ2v为，其它元素均为零。

滤波初值的选取：卡尔曼滤波是递推算法，需给定状态向量初始值 Φ（0）与初始估计均方误差矩阵[5]P（0）。 通常令 Φ（0）=0，同时令初始估计均方误差矩阵 P（0）=αI（其中 α 是比较大的正数，I为单位矩阵），这样可以保证滤波的结果是无偏的。

2 仿真实验

仿真过程中利用实测的卫星信号获取卫星的伪距，载波波长，多普勒频率等，代入已知量测方程和系统方程进行Kalman滤波，计算出下一时刻的载波相位计算值，与载波相位观测值比较，超过一定的误差范围则认为发生周跳。发生周跳时，可以用计算载波相位值的整数部分替代当前观测载波相位值的整数部分，当前观测载波相位值的小数部分保持不变[6]。

以NOVATEL双频接收机作为实验平台，采集实时数据（载波频率为1 575.42 MHz），通过数据预处理得到的载波相位的观测值如图1所示。

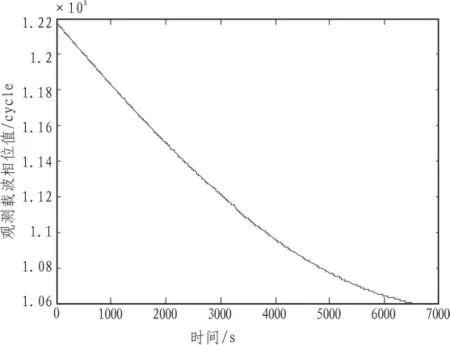
图1 观测载波相位值Fig.1 Observe the phase value of carrier wave

可选取1 000个历元进行计算，计算载波相位与观测载波相位的差值，如图2所示，说明计算值迅速收敛。进行局部放大，如图3所示。

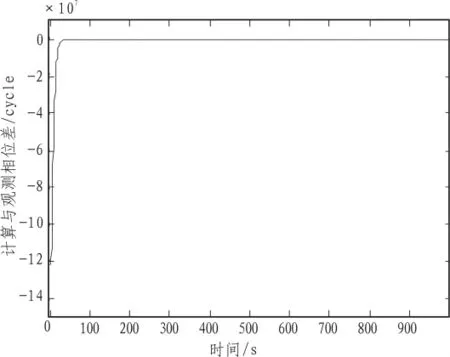
图2 观测与计算载波相位的差值Fig.2 Observe and calculate the phase difference of carrier wave

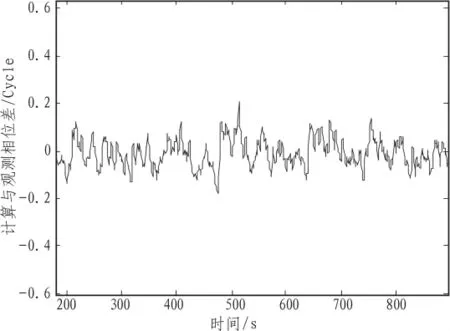
图3 局部放大后的差值Fig.3 Difference when it is partially enlarged

差值围绕零值上下波动，但在采样的时间里差值均小于门限值，说明没有发生周跳。在历元 400 s、600 s和700 s处分别加入-1周，2周和-2周的周跳，则从图4可以看出加入离散周跳的时刻的差值出现明显的跳变，成功地检测出周跳。在历元 399 s、400 s和401 s处分别加入2周，-1周和1周的周跳，则从图5可以看出加入连续周跳的时刻的差值出现明显的跳变，同样成功地检测出周跳。

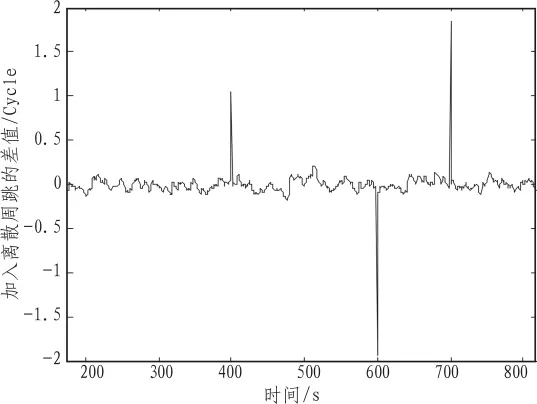
图4 加入离散周跳后的差值Fig.4 Difference when disperse cycle slip is added

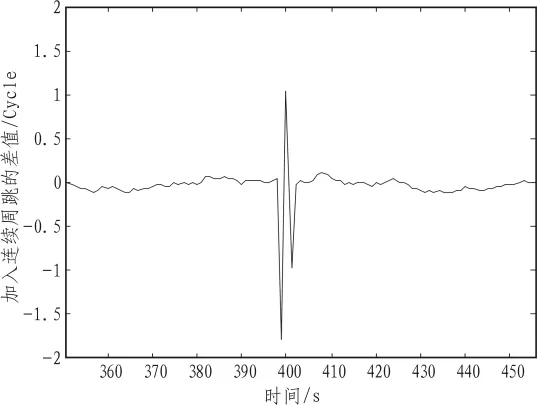
图5 加入连续周跳后的差值Fig.5 Difference when consecutive cycle slip is added

3 结 论

文中采用GPS的实时数据作为仿真的原始数据，从以上仿真可以看出，采用这种新的周跳检测方法可以很好地检测出周跳，对于连续的周跳，此方法的实用性也很高，同时针对了卫星的连续载波相位的跟踪探测。

[1]胡加星，刘立龙，宋元明，等.GPS周跳探测方法综述[J].全球定位系统，2010，35（4）：67-70.HU Jia-xing，LIU Li-long，SONG Yuan-ming，et al.Summary of GPS cycle slip detection method[J].Gnss World of China，2010，35（4）：67-70.

[2]李晓明，刘庆富，袁火平，等.基于BP神经网络修正的自适应Singer模型[J].微计算机信息，2008，24（6-1）：286-288.LI Xiao-ming，LIU Qing-fu，YUAN Huo-ping，et al.Adaptive singer model based on BP neural network modification[J].Microcomputer Information，2008，24（6-1）：286-288.

[3]程鹏飞，蔡艳辉，文汉江，等.全球卫星导航系统[M].北京：测绘出版社，2009.

[4]郁涛.基于多普勒频率的机载测距原理[J].信息与电子工程，2011，9（1）：22-25.YU Tao.Airborne ranging principle based on doppler frequency[J].Information and Electronic Engineering，2011，9（1）：22-25.

[5]李猛，文援兰，梁加红，等.基于卡尔曼滤波的周跳探测方法[J].测绘科学技术学报，2010，27（6）：407-411.LI Meng，WEN Yuan-lan，LIANG Jia-hong，et al.An algorithm of detecting cycle slips based on kalman filter[J].Journal of Geomatics Science and Technology，2010，27（6）：407-411.

[6]李征航，张小红.卫星导航定位新技术及高精度数据处理方法[M].武汉：武汉大学出版社，2009.

[7]张艳桃，袁兆强.基于双端不同步采样的同杆双回线故障测距算法[J].陕西电力，2009（9）:38-41.ZHANG Yan-tao，YUAN Zhao-qiang.Two-terminal asynchronous data based fault location algorithm for double-circuit transmission lines on one pole[J].Shaanxi Electric Power,2009（9）:38-41.