基于Turbo PMAC Clipper的伺服系统PID参数整定方法
2012-01-13邹丽梅
郭 波 邹丽梅
(武夷学院 电子工程系,福建 武夷山 354300)
基于Turbo PMAC Clipper的伺服系统PID参数整定方法
郭 波 邹丽梅
(武夷学院 电子工程系,福建 武夷山 354300)
本文介绍了PMAC测定PID参数软件PmacTuningPro2功能模块的运用,指明PID参数的变化对响应曲线指标的影响。分析了根据阶跃响应曲线整定PID参数方法与根据抛物线速度曲线整定前馈参数方法,为使用Clipper控制器开发机电设备打好基础。实践表明,此方法适合模拟输出速度环伺服系统,能提高显著提高系统响应速度等动态特性。
Clipper;PID参数;动态特性
在由PMAC控制器组建的高精度数控伺服系统中,当完成控制器、电机、传动结构与检测元件的选型构建后,就应当进行系统的自动控制调试。闭环数控伺服系统普遍采用的自动控制为PID(比例、积分、微分)控制,PMAC控制器还能引入前馈、滤波等算法,该控制对调校系统精度,获得良好动态特性有重要的效果。PMAC内置了PID算法,在实际调校中就是整定比例、积分和微分的三项参数值。工业控制PID整定方法到目前为止大约有几十种,如临界比例度法、反应曲线法、试凑法等[1],可是工业控制器及被控对象的特点千差万别,实际并没有一种适用于全部系统的精确整定方法。本文面向数控伺服系统,结合Turbo PMAC Clipper运动控制器PmacTuningPro2软件进行PID参数整定,通过总结整定流程,提高对类似系统的调试效率。
1 伺服系统的组成及PID软件介绍
Turbo PMAC Clipper控制器 (Turbo PMAC2 Eth-Lite)是美国Delta Tau公司推出的PMAC开放式多轴运动控制器家族的一员。其具备全部Turbo PMAC特征,提供最多32轴独立闭环控制,当前在我国主要用于数控机电产品开发。本实验伺服系统采用上位机+CLIPPER作为控制端完成信息处理;执行机构为日本富士伺服驱动器与电机(200W);机械本体采用X-Y十字滑台;反馈系统为伺服电机编码器,形成模拟输出,速度环闭环控制。
Clipper卡通过PmacTuningPro2软件为用户提供了PID、速度与加速度前馈和反馈滤波三类标准控制算法,这些需要整定的参数值以I变量的形式存储在卡内,点击菜单Interative Turing项可见PID参数集成整定对话框,如图1。

图1 PID参数集成整定对话框
该对话框涵盖了手动整定过程的全部参数设置,其中图中标示1~11项为PID参数设定区,用于手动输入需要测试的PID系列参数,分别为1、比例增益Kp;2、微分增益 Kd;3、速度前馈 Kvff;4、积分增益 Ki;5、积分模式 IM ;6、加速度前馈 Kaff;7、模拟量输出偏差;8、模拟量输出极限;9、伺服环周期扩展;10、摩擦前馈增益;11、跟随误差限制设定。这些参数存储在如图1所示变量Ixx30~Ixx11中,xx为电机号,Turbo PMAC2型控制器Clipper的取值范围为1~32。区域Ⅰ用于选择输入轨迹的类型,一般需要调整(1)Position Step阶跃位置信号输入,此整定过程涉及Kp、Kd、Ki、IM四个PID参数。阶跃位置输入信号在线性定常控制中为最差的激励信号,如果伺服系统能在此信号激励作用下满足控制要求,则其他外激励信号也就不会有问题。(2)Parabolic Velocity抛物线速度信号输入,用于调整速度前馈、加速度前馈、摩擦前馈增益这三个前馈参数。引入前馈环节能补充传统PID的精度控制缺陷,构成前馈反馈复合闭环,用于改善伺服系统速度误差与跟随误差。
区域Ⅱ用于设定输入信号参数值,现场调试应当尽量使输入参数接近伺服系统的运行工况。区域Ⅲ用于设定测出数据坐标轴的项目类型,可提供复合的测定曲线供调试人员参考。图1标示的按钮A用于被测电机的开闭,整定过程的操作为在PID参数设定区输入设定值后,鼠标点击按钮D运行内置的PLC程序开始测定指标,根据绘出的坐标轴曲线形状与测定指标更改PID参数,如此不断反复以便获得符合控制要求的动态特性。
点击按钮B (Notch Filter Calculator)或按钮C(Low Pass Filter Calculator)将进入陷波/低通滤波器调整模式,其涉及到Ixx36~Ixx39四个过滤器系数。该模式可自动整定过滤反馈噪音信号的过滤器系数,整定过程需要设定噪音频段。
2 PID参数的实际作用及曲线分析
PID参数在工程应用中可由理论计算和实验整定两种方法得到,当伺服系统参数不能完全掌握时,控制的结构与参数就必须依靠经验和现场调试来整定。依靠经验要求调试人员须了解PID参数代表的物理意义,该意义在许多文献均有详细说明[2];其次为掌握PID参数的变化对响应曲线指标的影响。
2.1 阶跃响应曲线
阶跃信号输入的响应曲线如图2所示,拥有阶跃指令位置线与实际位置线,比较两线差异得到指标,期望的指标应为:响应时间(Rise Time)应尽量小;带宽(Natural Freq)应尽量大;超调率(Over Shoot)应接近 0;阻尼比(Damping)维持在 0.6~1 之间。

图2 阶跃信号响应曲线
PID参数Ixx30比例增益的数值增加能提升系统刚性与响应速度,主要体现为曲线响应时间的减小、带宽的增加,阻尼比的减小。但是数值过大将影响系统的稳态特性,初始表现为超调率增大,响应时间增加。如果比例增益继续增加,系统将出现失稳,伺服系统将不断震荡。
Ixx31微分增益将引入阻尼。合适的数值增加能减低超调率,增加阻尼比,使伺服系统稳定在高比例增益下。如果微分增益数值过大,系统的响应时间将增大,带宽降低,阻尼比数值维持在1上。对于伺服系统,阻尼比应维持在0.6~1之间能够获得较好的响应特性。
Ixx33积分增益用于消除高比例增益带来的稳定误差,仅当伺服系统特性需要高比例增益带来高刚度或响应速度时才需要引入,一般系统采用默认值0即可。
Ixx34积分增益模式决定增益是否全程有效或控制速度为0时有效。
2.2 抛物线速度曲线
通过对抛物线速度曲线(如图3)的评估,可以发现伺服系统引前馈能减少系统跟随误差。所以,该曲线最重要的指标为最大跟随误差 (Max Following Error),其坐标值位于坐标轴右方,测定出的数值越接近0越好,单位为cts。
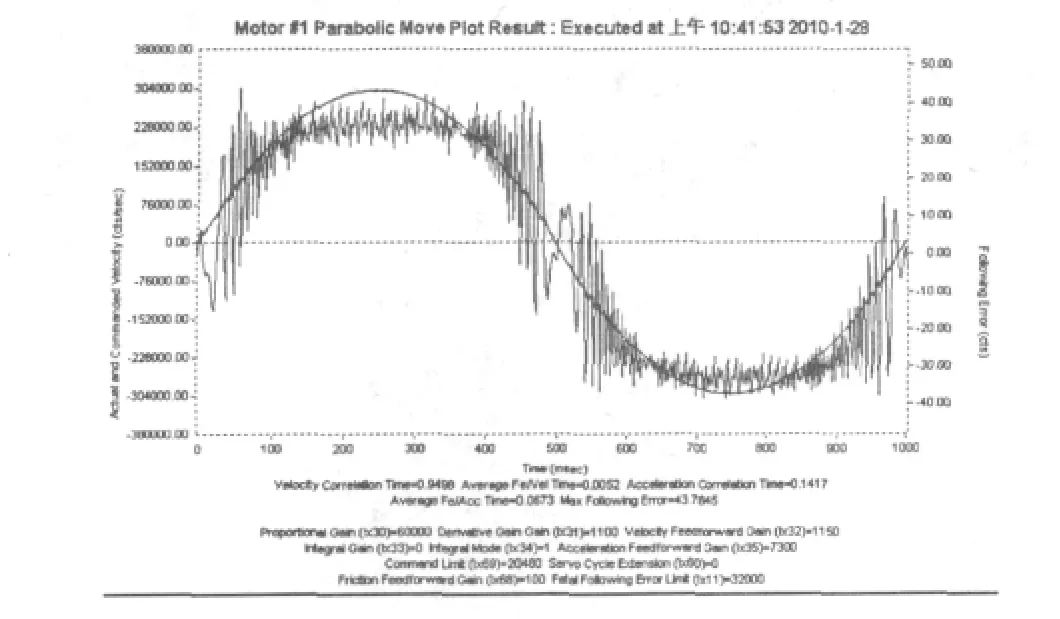
图3 抛物线速度曲线
Ixx32速度前馈可消除微分增益带来的跟随误差,Ixx35加速度前馈能减小系统惯性带来的跟随误差,Ixx68摩擦前馈增益能减小摩擦产生的跟随误差。
3 整定步骤及注意点
3.1 自动调定
PmacTuningPro2软件为用户提供了自动整定功能AutoTuning。该功能将快速运动电机并根据动态响应计算增益,但是遗憾的是该功能在多数带负载调整时并不能达到最优整定。自整定功能的用途主要在对系统的动态特性目标明确,且系统能达到的特性高于期望值很多的情况下。如果在负载条件下,自整定不能带来伺服系统希望的运动,那么只能手动整定电机伺服环的参数。关于自整定功能的使用,文献[3]有详细说明,这里不再赘述。
3.2 手动整定步骤
3.2.1 初始准备工作
1、将 Ixx30、Ixx31、Ixx32、Ixx33、Ixx34、Ixx35、Ixx60、Ixx68参数值修改为0。
2、选择菜单Position Loop中的DAC Calibration执行自动校正DAC,消除电机零飘,校正值输入Ixx29。
3、对于Clipper控制器,Ixx69设置应为1001,限制最大输出模拟电压值。
4、Ixx11设置为32000,限制测试最大跟随误差报警,防止不合适的PID参数引起系统超限震荡。
5、指令J/闭环电机,移动实验台至安全位置,通常为零点附近。
3.2.2 阶跃信号响应曲线的整定
第一步从较低的数值 (如100)开始,逐渐增加Ixx30比例增益,此时PID控制器为纯比例调节。随着数值的增加,将产生如图 4(a)至(d)四类曲线形状,其形状的意义见图4,与之对应的响应曲线指标开始变化:响应时间减小;超调率超过0;阻尼比(Damping)从1 开始逐渐下降至 0.1。在图(b)至图(c)阶段会出现响应时间随着数值的增加在最小的一个值保持毫秒级的跳动, 本实验系统为0.023s~0.025s。继续增加Ixx30,将会在某一数值,响应时间开始上升的情况,这时记录Ixx30的数值,取其70%作为初定值,则比例增益Kp确定。
第二步给定微分增益Ixx31一个较大的值,通常为Kp的两倍以上,测试结果一般来说,之前过大的超调率会减低为0,阻尼比会再次变为1,响应时间增大。这时逐渐减小微分增益,仔细观察曲线变化,根据指标响应时间变化,将会有一个合适的数值(此时可能需要微调比例增益Kp)控制响应时间达到第一步纯比例调节的最低值,同时带宽达到最大,如图4(d),至此阶跃信号输入整定完毕。
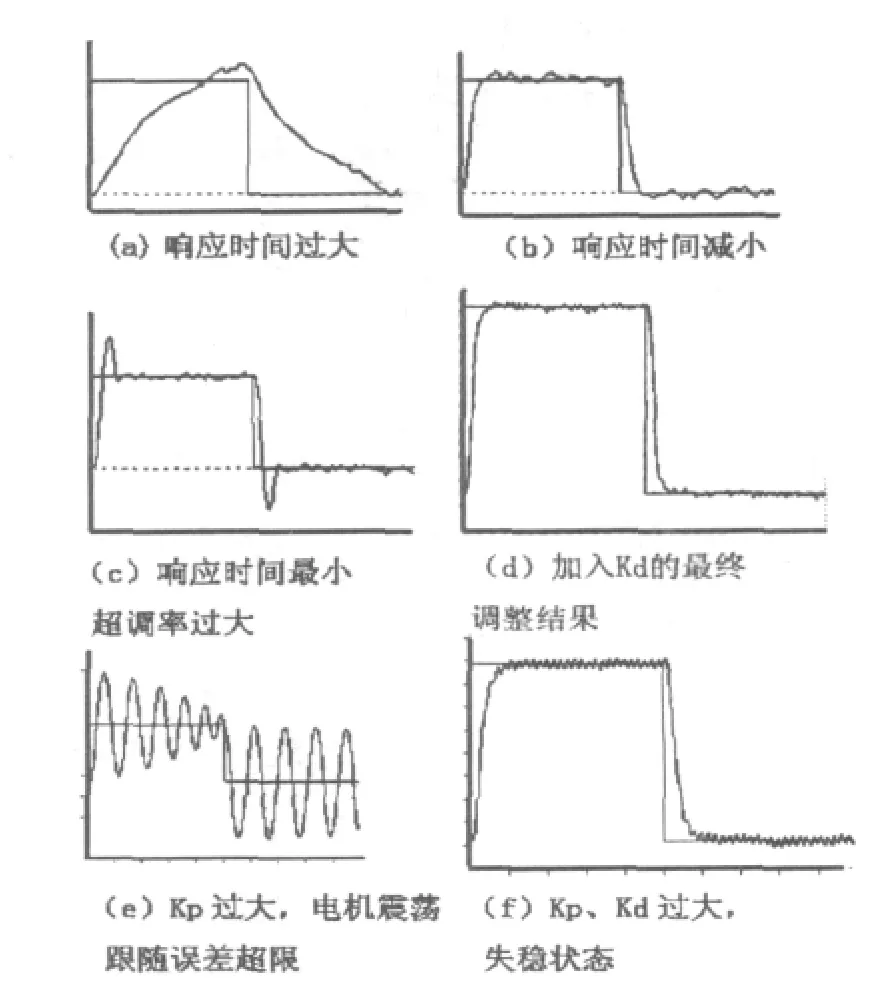
图4 常见阶跃曲线形状

图5 常见抛物线速度曲线形状
3.2.3 抛物线速度曲线的整定
在比例+微分控制条件下,选择抛物线速度输入,可以采用最小二乘法逐个输入Ixx32速度前馈参数,将得到的曲线与图5各阶段曲线形状对比。如Ixx32=1000曲线形状类似于图5(a),跟随误差线与指令速度线同相同位,属于速度前馈增益太小,再设定一个Ixx32=10000曲线形状类似图5(b),跟随误差反向,属于速度前馈增益太大,则再次输入5000对比,不断如此反复,直至得到一个最小的跟随误差值,如图5(c)。由于跟随误差有可能是负值,所以最小的值为最接近零的数值。
此时的跟随误差主要由系统惯性带来,最大误差集中发生在抛物线加速度变化最大处,如抛物线起点,中点和终点,从0开始逐渐增加Ixx35加速度前馈能减小这类误差,减低并稳定指标最大跟随误差(Max Following Error),如图 5(d)。但如果 Ixx35 数值过大也会增大最大跟随误差,所以不适用最小二乘法,只能通过不断比较曲线形状与特征值确定。
3.3 整定过程的注意点
1、检测到的指标是有误差的,同一组参数重复检测得到的指标并不会相同,但如果差异总是较大,说明反馈噪声影响较大,应尝试陷波滤波器设置。
2、比例增益与微分增益整定过程实际是一个寻找临界点的过程,比例增益需从小至大逐个尝试,微分增益应从大到小。如果随意尝试增益数值可能会带来较大的指标误差,对整定过程的曲线判断起干扰作用。
3、比例增益如果过大,测定时电机会震荡,如图4(e)此时应点击图1按钮A—killmotor关闭电机,减小比例增益再试。
4、在过高的Kp与Kd配合下,也可能获得较好的阶跃曲线指标,如图4(f)。但系统处于失稳状态,切换到抛物线速度曲线模式将引起过大的速度误差和跟随误差。
4 结束语
PMAC运动控制器用途广泛,受到广大机电工程人员的青睐。其PID参数整定是伺服系统正常工作的前提,是所有学习使用PMAC的工程师必须掌握的技术。由于其功能复杂,相关资料不全,其使用往往让初学者绕了很多弯路。笔者通过查阅资料、帮助文献并作实验对比,认为PMAC的整定过程是有规律可循的,希望此整定方法能对同行有所帮助。
[1]付冬梅.工业过程控制中的PID整定方法[J].自动化博览,1994(06).
[2]党大伟,武建新,杨晓军.基于PMAC-PCI运动控制器的PID 整定[J].机械工程与自动化,2009(03).
[3]赵保亚.基于PMAC的数控系统PID参数调节研究 [J].机械设计与制造,2007(10).
[4]DELTA TAU Data System,Inc.PMAC2Software Reference[Z],2004.
Based on the Turbo PMAC Clipper Serve System of PID Parameters Setting Method
GUO Bo ZOU Limei
(Department of Electronic Engineering,Wuyi University,Wuyishan,Fujian 354300)
This paper introduces the function module of software PmacTuningPro2 for PMAC setting PID parameters,point out The impact of PID parameters on the response curve indicators.Analysis the method of setting PID parameters by the step response curve and the method setting feed forward parameters by the parabolic velocity curve,the method can lay a basis for using the Clipper controller developing mechanical.The practice shows that this method is suitable for simulation output speed servo system,can improve the ring significantly improve the system response speed dynamic characteristics.
Clipper;PID parameters;dynamic characteristic
TM571
A
1674-2109(2012)01-0060-05
2011-10-08
南平市科技局项目(项目编号:N2009Z10-4)。
郭波(1979-),男,汉族,讲师,主要研究方向:数控技术。
