基于粒子群优化的连续发酵过程PID控制

刘毅，林传东，高增梁

（浙江工业大学化工机械设计研究所，杭州310032）

发酵过程的强非线性和自身特点造成其控制和优化较为困难。连续发酵过程菌体质量浓度的控制直接影响到最终产物质量和能量的消耗量，关系到企业的效益［1－2］。在能够保障和提高产品质量的前提下，应尽量选择简单和鲁棒性强的控制器，这也是比例－积分－微分PID控制器至今仍被广泛采用的原因［3－4］。通过参数整定方法获得优质的PID参数是提高过程控制质量的一种重要手段。因此，简单和高效的PID参数整定方法是值得研究的［3－4］。

据文献报道，目前广泛用于工业过程的PID控制器参数整定方法已超过200种，包括经典的Z－N和IMC等方法［4］。常规的PID控制器参数整定方法依靠经验。当过程对快速性、稳定性和鲁棒性等都有明确要求时，不易获得满足实际要求的最优PID参数。遗传算法等人工智能方法以其简单和快速收敛性为PID控制器参数的寻优开辟了一条新路［5］。但是，在优化具有参数强相关性的对象时，其搜索能力会变差，而且该算法存在过早收敛问题。

粒子群优化算法PSO（Particle Swarm Optimization）是一种全局优化算法，可用于解决非线性、不可微和多峰值复杂函数的优化问题，具有算法简单、容易实现、可调参数较少和应用效果明显等优点，获得了广泛的研究和应用［6－7］。最近，研究人员将PSO用于优化PID控制器的参数以提高控制效果［8］。但是，这类改进的PID控制器还很少用于发酵过程。因此，笔者针对发酵过程菌体质量浓度的控制问题，采用PSO优化PID控制器的参数，以获得更好的控制效果，最终提高发酵过程的控制质量。

1 PSO算法基本原理

PSO算法源于对鸟群和觅食行为的研究。研究者发现鸟群在飞行过程中经常会突然改变方向、散开、聚集，其行为不可预测，但其整体总保持一致性，个体与个体间也保持着最适宜的距离。通过对类似生物群体的行为研究，发现生物群体中存在着一种社会信息共享机制。它为群体的进化提供了一种优势，这也是PSO算法形成的基础［6－7］。

设zi＝（zi1，zi2，…ziP）为第i个粒子（i＝1，2，…，m）的P维位置矢量，根据事先设定的适应度函数计算zi当前的适应值，即可衡量粒子位置的优劣；vi（vi1，vi2，…，vid，…viP）——粒子i的飞行速度，即粒子移动的距离；pi（pi1，pi2，…，pid，…piP）——粒子迄今为止搜索到的最优位置；pg（pg1，pg2，…，pgd，…pgP）——整个粒子群迄今为止搜索到的最优位置。

在每次迭代中，粒子根据以下公式更新速度和位置［6－7］：

式中：d＝1，2，…，P；k——迭代次数；r1，r2——［0，1］的随机数，这两个参数用于保持群体的多样性；c1，c2——学习因子，也称加速因子；w——惯性权重，当w值取较大时，对全局搜索比较好，当w值取较小时，有利于局部搜索。式（1）等式右端的第二项是“认知”部分（cognition part），代表粒子对自身的学习。式（1）等式右端的第三项是“社会”部分（social part），代表着粒子间的协作。式（1）是粒子根据其上一次迭代的速度、当前的位置和自身最好经验与群体最好经验之间的距离来更新速度。然后粒子根据式（2）飞向新的位置。根据式（1）和式（2）对微粒的速度、位置进化，直到满足最大迭代的代数或满足所要求的精度为止［6－7］。

针对连续发酵过程的PID控制器参数优化问题，为了提高搜索效率，保证PSO算法在前期具有良好的全局搜索能力，后期要有良好的局部搜索能力，故让w呈线性递减，即：

式中：wmax＝0.9；wmin＝0.5［6－7］；t——当前迭代次数；Nmax——最大迭代次数。按照经验，本文PSO算法的参数选择如下：最大迭代次数为20，粒子个数为10个，c1＝c2＝1.5［6－7］。

2 连续发酵过程的仿真和讨论

2.1 连续发酵过程

所研究的连续发酵过程由以下微分方程组描述［9－11］：

式中：D——稀释率；X——菌体质量浓度；S——底物质量浓度；P——产物质量浓度；Sf——流加底物质量浓度；μ——比生长率，表现出典型的底物和产物抑制；μm——最大比生长速率；Pm——产物饱和常数；Km——底物饱和常数；Ki——底物抑制常数；Yx／s——菌体对底物的得率系数；α，β——动力学参数，其参数值和发酵操作条件见文献［9］。D通常作为调节变量，X，S，P都可作为输出变量。文献［9］的研究表明，通过合理控制X能够获得最优的生产能力。因此，文中选择X作为被控变量。

图1给出了发酵过程的示意图，通过调节D实现对X的控制。Henson和Seborg［9］采用IMC方法整定了相应的PID参数。文献［10］等设计了一种基于多项式的自校正控制器，其效果略优于整定的PID，但控制器设计复杂，且随多项式次数增加计算存在困难。文献［11］则采用模糊预测控制器，但需要大量样本（2 500个）用于建立模糊模型，且模糊规则通常较难确定。因此，这两类控制器都难以在实际发酵过程中得到应用。本文采用PSO优化PID控制参数，故相应的控制方法记为PSO－PID。

图1 连续发酵过程及其PID控制器

2.2 仿真比较及讨论

文献［9］采用IMC方法整定了一组PID参数。但是，发酵过程往往表现出生长率不一致的多阶段特性，X在不同区间反映出不同的生长特点，仅靠单一优化的PID参数通常无法同时满足各阶段的控制性能要求。因为X和最终的产物收率相关联［9］，所以，笔者采用多模型思路，提出将该连续发酵过程按照X值简单划分成三个子过程，并分别通过PSO优化每个区间的PID参数，获得三个子区间的PSO－PID控制器。

比较方法包括传统的、基于IMC优化的PID控制器，记为PID。此外，在IMC优化PID参数的基础上，对每一个子过程再通过网格搜索GS（Grid Search）获得一组PID参数，记为GS－PID。实际过程中，如果控制器大幅度、高频率进行调节，会降低执行阀的使用寿命。因此，文中约束调节变量D，使其每次变动范围为±0.5。

表1给出了PSO－PID，GS－PID，PID 3种控制器针对连续发酵过程不同质量浓度区间的X控制性能比较，包括过程有无噪声两类情况（实际发酵过程肯定有噪声，此处讨论的无噪声情况可视为噪声很小时的近似情况）。控制器的性能指标采用常用的误差平方积分指标ISE（Integral Square Error）。

当过程不加入噪声干扰时，X在高、中、低三种质量浓度下的控制结果比较分别如图2～4所示。PSO－PID的控制性能是最好的，GS－PID也能够获得比传统的PID更好的控制性能。当过程加入噪声干扰时，X在高、中、低三种质量浓度下的控制结果比较分别如图5～7所示。此时，PSOPID的控制性能依然是最好的。而在中质量浓度区，GS－PID的结果变得很差，很难对给定值进行跟踪。在低质量浓度区，GS－PID与PID的控制性能十分接近。

从表1的性能指标比较和图2～7的结果可以看出，IMC优化的PID参数其实更适合高质量浓度和中质量浓度区间的控制，因为各种质量浓度区间的控制一开始都有偏向高质量浓度的趋势。该发酵过程中，各个子区间优化得到的PSO－PID控制器参数是不同的。因此，采用多区间设计PSOPID控制方案是合理的。GS－PID是对传统PID优化参数进行再搜索，从而也表现出只适合高质量浓度区间的控制。因此，这一类没有进化能力的普通搜索方法的优化效果非常有局限性，尤其是针对的过程存在一定程度的噪声时。

针对该发酵过程，PSO优化PID控制器的程序运行时间约15min，而GS优化PID控制器的程序运行时间约1h，PSO优化效率更高。此外，针对该过程，PSO算法效率提高的原因是采用了式（3）的加速搜索策略。仿真表明，采用该策略的时间比不采用该策略时间减少了一半以上。因此，通过以上的讨论，最终可以得出所提出的多区间PSO－PID控制器的性能明显优于传统的PID控制器的结论。

表1 3种PID在不同质量浓度区的控制结果比较kg／m3

图2 PSO－PID和其他控制方法性能比较（高质量浓度下无噪声）

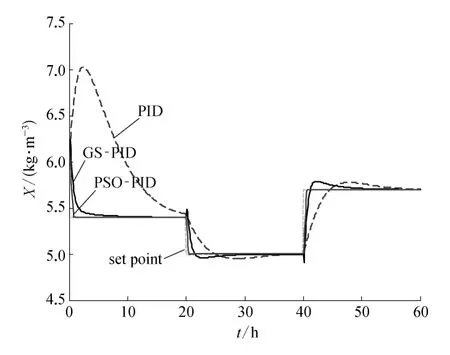
图3 PSO－PID和其他控制方法性能比较（中质量浓度下无噪声）

图4 PSO－PID和其他控制方法性能比较（低质量浓度下无噪声）

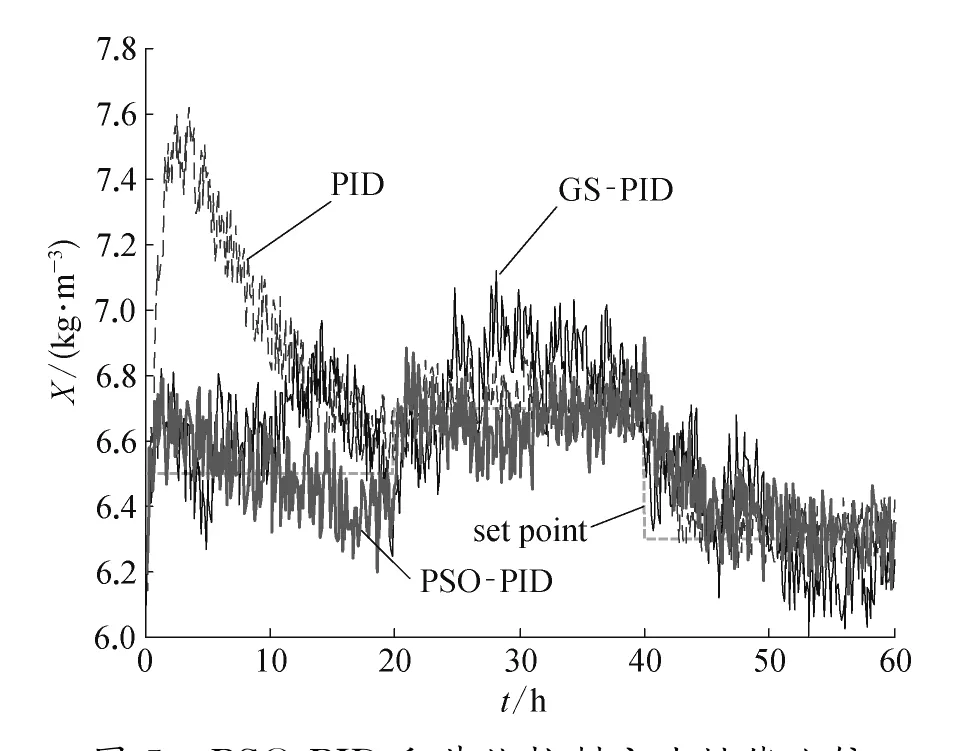
图5 PSO－PID和其他控制方法性能比较（高质量浓度下有噪声）

图6 PSO－PID和其他控制方法性能比较（中质量浓度下有噪声）

图7 PSO－PID和其他控制方法性能比较（低质量浓度下有噪声）

3 结束语

研究简单高效的控制算法是具有实际应用价值的。PSO是一类具有进化能力的全局优化算法。针对一类连续发酵过程，笔者按照菌体质量浓度特点将其分为三个子过程，并通过PSO优化每一个子过程的PID控制器参数。仿真结果表明，所提出的PSO－PID控制器的控制质量要优于传统的PID控制。

［1］ ALFORD J S.Bioprocess Control：Advances and Challenges［J］.Computers and Chemical Engineering，2006，30（10）：1464－1475.

［2］ 史仲平，潘丰.发酵过程解析、控制与检测技术［M］.北京：化学工业出版社，2010.

［3］ LI Y，ANG K H，CHONG G C Y.PID Control System Analysis and Design［J］.IEEE Control Systems Magazine，2006，26（01）：32－41.

［4］ OGUNNAIKE B A，MUKATI K.An Alternative Structure for Next Generation Regulatory Controllers Part I：Basic Theory for Design，Development and Implementation［J］.Journal of Process Control，2006，16（05）：499－509.

［5］ TAN W W，LU F，LOH A P，et al.Modeling and Control of a Pilot pH Plant Using Genetic Algorithm［J］.Engineering Applications of Artificial Intelligence，2005，18（04）：485－494.

［6］ 纪震，廖惠连，吴青华.粒子群算法及应用［M］.北京：科学出版社，2009.

［7］ 刘波.粒子群优化算法及其工程应用［M］.北京：电子工业出版社，2010.

［8］ 金翠云，王建林，马江宁，等.改进的PSO算法及其在PID控制器参数整定中的应用［J］.电子测量与仪器学报，2010，24（02）：141－146.

［9］ HENSON M A，SEBORG D E.An Internal Model Control Strategy for Nonlinear Systems［J］.AIChE Journal，1991，37（07）：1065－1081.

［10］ RADHAKRISHNAN T K，SUNDARAM S，CHIDAMBARAM M.Non－linear Control of Continuous Bioreactors［J］.Bioprocess Engineering，1999，20（02）：173－178.

［11］ VENKATESWARLU Ch，NAIDU K V S.Dynamic Fuzzy Model Based Predictive Controller for a Biochemical Reactor［J］.Bioprocess Engineering，2000，23（02）：113－120.