温度计保护套管的性能研究

汉建德，华霄峰

（1.中石化宁波工程有限公司，浙江宁波 315103；2.浙江拓峰科技有限公司，杭州 310012）

温度是一个基本的物理量，它是各类生产过程中应用最普遍、最重要的工艺参数。按照温度测量仪表的感温部分是否与被测介质相接触，可分为接触式与非接触式两大类。接触式的温度仪表（热电偶、热电阻、双金属温度计等）用于工业管道中进行温度的测量时，一般情况下都要配用温度计保护套管。

保护套管的性能涉及到强度和各种热效因素。一般来说，保护套管壁厚的增加能提高应力强度，但是壁厚的增加会增加传感器的热惰性，即传感器对温度反应变慢。保护套管各要素（不包括材料特性和结构形状等）之间的关系见表1所列。

表1 温度计保护套管各要素之间的关系

从表1中可以看出，设计和选用一个“合适”的保护套管，需平衡各种因素，以达到多快好省的目的。导致保护套管损坏的原因：保护套管在使用过程中承受了外部的静态压力、稳态流体的冲击力和振动荷载后，在其内部所产生的应力超过了材料本身的许用应力。因此，在保护套管设计和选用时，通过计算来确定材料本身的许用应力和使用过程中产生的应力之间的关系成为保证保护套管安全使用的关键。文献［1］就“温度计套管的振动频率内容”进行过简单的探讨，随着对此问题的不断关注以及相关标准的更新，笔者就温度计保护套管的性能、振动以及受力分析等内容作进一步的研究，以期与各位同行共同探讨。

1 保护套管的计算

1.1 保护套管计算的假定

保护套管计算主要从保护套管的振动和受力两方面考虑，而且在计算前必须做部分的假定，否则计算将无法进行。

a）假定保护套管沿其轴向（即管道径向）承受均布载荷。事实上，流体（如气流）在管内流动时，其速度分布呈抛物线型，沿管道径向各点流体的速度是不同的。

b）假定保护套管仅受外压，内压等于零。

c）假定套管的阻尼因素为零（即套管的振动为无阻尼的强迫振动）。

d）假定卡曼涡流形成的力等于流速压力。

上述这些假定，都是为了计算方便而给出的简化条件，同时也是保守而安全的假定。实际中套管的振动肯定存在一定的阻尼，而且卡曼涡流形成的力也是低于流速的压力。

1.2 保护套管的振动

当测量流动介质时，介质会有外力作用于保护套管上，这种力的作用所产生的激励频率fs愈接近保护套管自身的自然频率fn时，振动就会加剧；当fs＝fn时，温度计套管将由于强烈振动而损坏。这种现象叫做“共振”，在力学上也称之为“拍”的现象。

当流体流经保护套管时，由于保护套管对流体的遮挡作用导致流体的动量发生改变，而这将会在套管后部产生一个湍流尾流，并且这个尾流内会形成一个漩涡（卡曼漩涡）。卡曼漩涡直接作用于套管体上，对套管会产生两种周期性变化的力：流向力方向是沿着流体流动的方向；横向力与流体流动方向垂直。如图1所示。

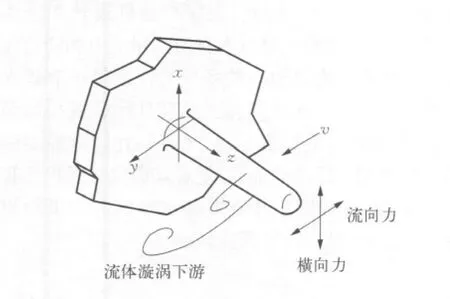
图1 温度计保护套管受力示意

1.2.1 fs的确定

当保护套管套入到被测介质时，在振动载荷的冲击下会产生无阻尼的强迫振动，此时保护套管被施以外力频率振动。此外力频率即为卡曼涡流产生的斯特劳哈尔（Strouhal）频率（也称激励频率），用fs表示。根据流体力学的相关理论得知，fs与介质流速成正比，与保护套管端部直径成反比，其计算公式为

式中：v——介质的流体流速，m／s；B——保护套管的端部外径，m；Ns——斯特劳哈尔系数，是一个无量纲的常数，它与管道中介质的雷诺数Re有关。对于圆柱体而言，Ns的确定可以通过查表或计算得出，计算公式如下：

Re与套管的端部外径、流体介质动力黏度、动黏滞率以及流体介质的密度有关，其计算公式如下：

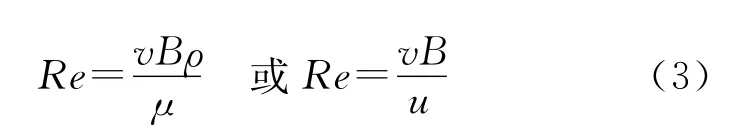
式中：μ——动态黏滞度；u——动黏滞率；ρ——流动条件下的流体密度。

在保护套管的设计选用过程中，Ns也可以经简化后，取一个较为保守的数值进行计算：

若Re近似为100，则Ns受流体黏度的影响将很小；若Re在103～5×105，只需保证此黏度在因数2以内；若Re大于5×105，则可以查阅相关参考文献来获得典型的黏度数值；如果黏度很难确定，则使用式（4）来计算Ns。

1.2.2 fn的确定

任何一个有质量的物体，均有其固有频率或称自然频率，用fn表示。决定保护套管fn的因素包括套管直径（包括外径和内径）、长度（包括外部长度和内孔长度）、套管的弹性模量、密度、被测介质的操作温度等。其中套管材料的弹性模量和密度将随着介质的操作温度升高而下降，并且弹性模量的降低要比密度的降低大得多。

关于fn计算，目前常用的有ASME PTC 19.3 TW—2010中所描述的方法、李滋法计算方法、天津中环温度仪表有限公司的“有限单元法”，除此之外还有雷列能量法、邓克利累加法等。下面将介绍几种常用的计算方法。

1.2.2.1 ASME PTC 19.3TW—2010中所描述的方法

在ASME PTC 19.3TW—2010第6.5节（保护套管的自然频率）中，对于怎样确定一支温度计保护套管的fn有较为详细的描述。温度计保护套管的自然频率是以下参数的函数：套管的弹性模量；套管材质的密度；小数值L／A的切变与转动惯量；支架匹配度；流体附加的质量；传感器附加的质量。

在该标准中，fn的确定是通过将一系列校正参数应用到一个将实际温度计套管直径进行平均的理想化的模型上，从而建立了fn的保守估计算法。同时该标准也认为，虽然一个温度计套管有无穷多个振动方式，但基频fn1是决定能否诱发共振的最主要因素，因而在计算fn时主要考虑fn1即可。基频fn1的计算和修正步骤如下：

步骤1：计算温度计套管的平均外径Da。对于圆柱形温度计套管，Da是圆柱的外径；对于锥形温度计套管，设Da＝（A＋B）／2；对于阶梯形的温度计套管，设Da＝A。

步骤2：计算温度计套管的近似自然频率：

式中：E——保护套管材料在使用温度下的弹性模量，KPa；I——第二转动惯量，I＝π（D4a－d4）／64；L——套管长度，m；m——套管每单位长度的质量，m＝ρmπ（D2a－d2）／4。

步骤3：计算校正参数Hf。对于圆柱形或锥形的温度计套管，使用关系式：

式中：A——温度计套管的根部直径；Da——温度计套管的平均外径，Da＝（A＋B）／2；d＝温度计套管的内径。

对于阶梯形温度计套管，使用关系式：

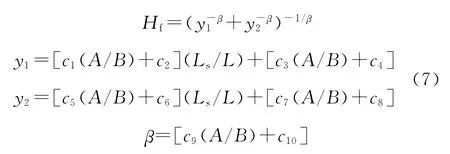
式中：ci——参数，可在文献［2］中第6.5.3节中查询；Ls——温度计套管小直径部分的长度。不允许对表6－5.3－1记录的数据进行插值，尽管设计者可以用近似的横柄模型或有限元法来确定其他尺寸温度计套管的Hf。

对于（L／A）＞10和A＝B的细长的温度计套管，Hf的值将近似为1；对于短的或那些A≠B的温度计套管，Hf的数值将根据具体的锥度比、内径及存在的阶梯数来决定，数值近似为0.6～1.5。

步骤4：计算流体的附加质量修正参数Ha，f：

或者作为另一种选择，对于蒸汽或类似低密度的气体设Ha，f＝1.0，对液态水设Ha，f＝0.94。对于高密度的液体，Ha，f也许会大幅减小（比如，对流体密度为1 600kg／m3和密度为8 000kg／m3的温度计套管设置Ha，f＝0.90）。

步骤5：计算传感器质量修正参数Ha，s：

式中：ρs——套管内的温度计的平均密度；ρm——温度计套管材料的密度。对一个具有可压缩的、无极隔绝的、金属覆盖构造的传感器（热电阻温度计或热电偶），一个典型的传感器密度为ρs＝2 700kg／m3（169lb／ft3），这个数值应在传感器设计时缺乏详细信息时使用。另外，对一个直径标称为6.35mm（0.25in）的传感器设置Ha，s＝0.96，或者对一个直径为9.53mm（0.375in）的传感器设置Ha，s＝0.93。

步骤6：温度计套管的自然频率（基频fn1）为

1.2.2.2 李滋法计算方法

李滋（W.Ritz）是19世纪后期在振动力学发展史上具有重要贡献的一位力学家。他不但找到了求解复杂系统fn1的计算方法，而且还成功地解决了求解系统的高阶频率和主振型的途径。李滋法是基于保守系统能量守恒原理的一种计算方法，这种方法求得的近似值与相应的精确值相比偏大。

采用李滋法在计算保护套管的振动时，将保护套管视为一个多自由度的系统。虽然李滋法在计算fn时不但可以计算基频，还可以计算高频，但是对于一般的工程设计而言，保护套管fn只需计算fn1即可。同时由于计算过程中为了确定边界条件和简化计算过程，下面计算fn1的方法仅适用于锥形保护套管（即变截面梁，结构示意如图2所示）的纵向振动，对于圆柱体而言，公式在总结过程中是给不了定解的。

图2 圆锥形保护套管的结构示意

李滋法计算方法的基本公式如下：

式中：E——保护套管材料在使用温度下的弹性模量，kPa（保护套管材料的密度和弹性模量可在文献［3］中查询）；D——锥形保护套管的外根部外径，m；d——锥形保护套管的外端部直径，m；d0——锥形保护套管的内孔直径，m。

1.2.2.3 天津中环的“有限单元法”

天津中环温度仪表公司研发的计算fn“有限单元法”是企业自身经过多年的生产实践并结合先进科学理论开发出的计算方法，该方法已申请专利，并已原始取得了“热安装套管fn计算程序V1.0”的软件著作权（软件著作权编号：软著登字第0145085号）。笔者在此也仅简介其原理，供读者了解。

“有限单元法”的核心思想是结构的离散化，就是将实际结构假想地离散为有限数目的规则单元组合体，实际结构的物理性能可以通过对离散体进行分析，得出满足工程精度的近似结果来替代对实际结构的分析，这样可以解决很多实际工程需要解决而理论分析又无法解决的复杂问题。单元越小（网络越细）则离散域的近似程度越好，计算结果也越精确。后处理则是采集处理分析，从而得出计算结果。

“有限单元法”求解问题的基本过程主要包括分析对象的离散化、有限元求解、计算结果的处理三部分。“有限单元法”是目前国际上应用于工业领域最先进最准确的计算方法之一。其利用“一分一合”的基本思想，进行单元分析和整体结构的综合分析，可以将任何复杂的连续体结构进行准确有效的数值分析，从而得出准确的结论。

1.2.2.4 雷列能量法

按照雷列能量法利用图解方式计算保护套管的fn。关于图解法原理、具体方法和步骤等在材料力学和有关书籍中已有述及，在此不再赘述。雷列能量法是指在以一定仔细程度作图的情况下，图解法求得的结果。此方法对于实用的目的而言，还是足够正确的。它的大致步骤如下：a）将所研究的零件分成若干段ΔXi，分别求出ΔXi段的质量及其重心；b）作出力多边形和索多边形及它的弯矩图并计算虚轴上的虚载荷；c）作出虚轴上的弯矩图；d）绘制相当弯矩图并定出虚力；e）求得各断面的静力挠度yci；f）按照雷列能量公式计算其基频fn1。雷列能量法对于一般的工程设计而言并不适用，此处的介绍也仅作为了解即可。

1.2.3 fn与fs的关系

1.2.3.1 共 振

共振发生时，强迫振动的振幅会随时间线性增大，需要经过无限长的时间，振幅才能达到无穷大。也就是说，共振需要一个相当长的建立过程，许多设备、机器（例如涡轮发动机）在正常运行时，激励频率肯定是远远超出系统的自然频率。但是在系统开车或停车过程中，都需要越过“共振区”，这也就是温度计保护套管的断裂为什么出现在装置开、停车期间甚至在系统吹扫期间的原因。对于机器而言，只要有足够的加速功率，一般是可以顺利通过共振区而不致于发生过大的振幅，必要时可以采用限幅器；但是对于保护套管而言，这种方法无法实现。因此，在工程设计过程中，只能根据fs和fn产生的机理和制约的因素，调整各自的数值，使两者最终达到“和平共处”。

1.2.3.2 fs和fn的限制关系

根据ASME PTC 19.3TW—2010中第6.8节（频率限制）中的最新描述得知：当流体经过保护套管时，保护套管会受到两种周期性变化的力：垂直于流体流动方向的横向力（将会产生激励频率fs）；平行于流体流动方向的流向力（将会产生激励频率2fs）。随着流体流速增加，涡旋脱落速率也线性地增加，与此同时，应力的大小随流体流速的平方增加。温度计套管根据应力的分布及变化做实时的弹性响应。当fs＝fn时，将发生共振并伴随动力学弯曲应力的显著增加。该共振发生时的流体流速被称为临界流速。每个温度计套管的fn都对应有两个临界流速的最小值：一个描述横向力，另一个描述流向力。

如果保护套管的fn与fs或2fs有部分重叠，会产生一个振动幅度很大的共振，从而导致保护套管故障（如图3所示）。因为fs与流体流速v成比例关系，流向共振发生的速率为横向共振的一半。尽管存在的流向力很小，但由于典型保护套管的低阻尼特性还是会导致很大的振动幅度。图4阐明了振动幅度与流体流速的变化规律。

由于保护套管的弹性响应与涡旋脱落过程联系如此紧密，所以即便实际的涡旋脱落过程是非线性的，仍有望根据保护套管的结构共振来捕捉与锁定。在fs接近保护套管的fn时进行捕捉。随着横柄的响应，涡旋脱落率会趋向于稳定在横柄的共振频率，并保持锁定在一个相当大的流速范围内。温度计套管的fn可能高达几千赫兹；由于伴随有锁区现象，使得一个温度计套管会在一次启动过程中遭遇上千次的疲劳周期，甚至涡旋脱落率与处于稳定工艺条件下的温度计套管的fn不匹配。

为了防止锁区现象的发生，并且将产生的振动幅度限制在一个安全的数值范围内，所安装的温度计套管的共振频率应该足够高于共振条件。只有当周期应力在共振条件下小得足以接受时，才允许超过流向共振限制情况下使用温度计套管。但是对于工程设计人员而言，即使一个温度计套管足够强韧以致能够承受流向共振，流向共振下的顶端振动也会是极大的，从而导致传感器衰退或损坏。

a）低密度流体的频率范围。对于Re＜105的且密度足够低的流体，温度计套管本身的阻尼足以抑制由涡旋脱落而产生的流向共振。普通温度计套管的固有阻尼系数ζ应保守地设置为0.000 5。

如果NS＞2.5且Re＜105，流向共振即被抑制，所安装的温度计套管的自然频率应满足：

如果NS＞64且Re＜105，那么流向与横向的共振都可被抑制。流体的流速可以超出式（12）的限制，但是应该考虑是否会激发高阶温度计套管共振。

b）一般情况的频率范围。如果NS≤2.5或Re≥105，可按照1.2.2.1节中描述的方法确定温度计套管的频率范围。此时如果温度计套管超过了在流向共振条件下允许运算的周期应力条件，则其安装的fn应满足式（12）。

如果温度计套管不符合在流向共振条件下允许运算的周期应力条件，则fn应足够大足以限制流向共振的激发，如图3和4所示。fn应满足：

c）当流向共振没有限制运算时的频率范围。在温度计套管超出流向共振条件下运算的周期应力条件的例子中，应注意在稳定状态下流体条件与温度计套管的共振是不匹配的。稳态的流体流速应满足以下的条件之一：

或者

形象地说，这些条件相当于介于图3两灰色方块之间的流体流速来进行运算。

1.3 保护套管的受力

保护套管的受力是指保护套管在使用过程中承受了来自于其外部的静态压力、稳态流体的冲击力和受振动荷载后，在其内部所产生的应力，当这种应力超过了材料本身在使用温度下的许用应力时，保护套管的使用安全性就无法得到保障。对温度计保护套管而言，不同的材料在不同的温度下所能承受的最大许用应力是不一样的。具体数值可在文献［3］中查询。

在保护套管使用过程中，其材料在使用温度下的许用应力小于测量介质对其的作用力时，保护套管将会被破坏，温度测量的准确性、安全性也就无从谈起。在测量过程中，测量介质对保护套管的作用力主要有：流体动压力产生的弯曲应力和流体对保护套管的静压力。

1.3.1 流体动压力产生的弯曲应力

在测量过程中，当温度计保护套管插入到流体中时，则有动压力作用于保护套管端部，其根部则为危险断面，此处所承受着由于弯矩而产生的最大弯曲应力σ。σ的计算公式如下：

式中：CD——阻力系数，它将考虑到沿保护管周围流体阻力分布是不均匀的。其中阻力系数CD取决于插入到流体中的保护套管形状，而投影面积S（见图2圆锥形保护套管的结构示意图）则由下式求得：

当然阻力系数也可在文献［3］中查表获得。

1.3.2 流体对保护套管的静压力

保护套管在测量时除了受到流体压力产生的弯曲应力以外，还将受到来自流体介质的外压以及半径方向与切线方向的径向应力和切向应力。

这两种应力可由下式求得：

式中：σr——在半径r的径向应力；στ——在半径r的切向应力；p——作用在保护管的外压，Pa；r1——保护管的内半径，cm；r2——保护管的外半径，cm；r——任意位置的半径（r1≤r≤r2）。

一般可假设，保护套管内的内压为0，则根据流体力学的理论得知，流体静压产生的最大应力应该是在圆的内侧面产生的切向应力。最大切向应力可由下式求得：

根据第四强度理论和力的叠加原理，对于保护套管的计算，即就是确保保护套管所受的总应力σ（最大弯曲应力与最大静压力之和）小于保护套管材料的最大许用应力，否则套管将会被损坏。

2 保护套管设计中改进的措施

根据以上的理论分析和实际的工程设计经验，温度计保护套管设计过程中应该对每一支套管进行振动和受力的计算。如果计算结果不满足相关要求，则必须进行改进。对于设计人员而言，按照下列几条措施改进后，最终可确保保护套管的安全，实现温度仪表的准确测量。

2.1 选择合理的套管材料

因为各种材料在不同的温度、压力下其性能差别很大，所以材料的选择是设计套管的第一步，也是最为关键的一步。材料选择的原则：能够承受被测介质的温度与压力；高温下物理与化学性能稳定；高温机械强度好，能够承受振动、冲击等机械作用；耐热冲击性能良好，不因温度急变而损坏；足够的气密性；不产生对测温元件有害的气体；导热性能良好；对被测介质无影响，不粘污；根据介质特性，需具有不同程度的耐磨防腐。

2.2 改变套管的内外径

在实际工程设计中，通常用“增大套管外径，减小套管内径”的办法，此办法增加了结构的固有频率，可以错开共振危险区。当然，在不影响相应时间的情况下，增加套管外径和壁厚，可以达到很好的效果。

2.3 改变温度计的安装位置

在安装温度计时，错开管道弯道、阀门、节流孔板附近等位置，以防止速度扰动，引起某一振动。通常可以将套管的安装位置选在弯头处，因为在弯头处流体流速比较低，但是低流速处温度测量的热交换不够充分，热响应速度会较慢，所以这条措施的采用需要在工程中慎重选择。

2.4 改变保护套管的外形结构

温度计保护套管从外形来分，主要有锥形套管、直形（即圆柱形）套管和阶梯形套管，其强度由强到弱排列顺序为锥形套管—直套管—阶梯形套管。因此，出于安全的考虑，建议尽量选用锥形保护套管。

2.5 缩短套管长度

缩短保护套管长度能有效提高套管固有频率，并提高套管强度。此方法也是实际中常用的方法，但缩短多少要看具体情况。当此温度信号作为控制信号时，缩短的长度是有限的，否则影响测量精度和响应时间，进而影响控制质量。但如果此信号只为显示信号，例如就地双金属温度计等，既不参与控制，可缩短的长度相对可以多一些。

2.6 增加其他辅助装置

如果上述几条措施实施以后还无法满足相关要求，则可以增加其他辅助装置的方法。具体措施为在保护套管的插入端增加一个保护圈，起到支撑作用。这样缩短了悬臂的长度，大幅减小了套管尖端的振幅。采用此改进措施的注意事项：保护圈和支管之间的距离公差为1mm，且支管内部需要打磨光滑以便于安装，如图5所示。

图5 保护套管保护圈

3 结束语

温度计保护套管的计算在工程设计中越来越受到重视，但是目前设计人员以及制造厂对于计算的方法，应该采用的标准，计算过程中应该注意的事项等有诸多争议。笔者在总结各位同行以及部分制造厂实际经验的基础上，列出了套管计算的几种方法和相关步骤，还提出了部分改进措施，采用这些改进措施能很方便地对不合理的套管尺寸进行重新设计，从而保证了温度计套管在使用中的安全性。但需要注意的是，保护套管的计算适用于流体流动测温的情况，而当测温流体处于静止状态时不需要对温度计套管进行计算。

［1］ 汉建德，郭峰，赵琼.温度计套管的计算［J］.石油化工自动化，2007，43（04）：69－70.

［2］ MCHALE M P，FRIEDMAN J R，KARIAN J H，et al.ASME.PTC 19.3TW—2010Thermowells Performance Test Codes［S］.ASME，2010：12－20.

［3］ FELDSTEIN J G，PASTOR T P.ASME Boiler and Pressure Vessel Code，Section II—Unfired Pressure Vessels［S］.ASME，2010：16－86.

［4］ 陆德明，张振基，黄步余.石油化工自动控制设计手册［M］.3版.北京：化学工业出版社，2000.

［5］ 游伯坤，阚家钜，江兆章.温度测量与仪表—热电偶和热电阻［M］.北京：科学技术文献出版社，1990.

［6］ 王魁汉.温度测量实用技术［M］.北京：机械工业出版社，2006.

［7］ 谢官模.振动力学［M］.北京：国防工业出版社，2011.

［8］ 蔡武昌，孙淮清，纪纲.流量测量方法和仪表的选用［M］.北京：化学工业出版社，2001.

［9］ 范玉久，朱麟章.化工测量及仪表［M］.北京：化学工业出版社，2001.

［10］ 孙海，李兆明.温度计套管的性能测试计算［J］.石油化工自动化，2008，44（04）：17－20.

［11］ 刘汉杰，王发兵，胡同印，等.有限单元法在温度计套管振动计算中的应用［J］.石油化工自动化，2009，45（05）：65－67.

［12］ 于洪波，李霞.热电偶套管断裂的原因分析及预防措施［J］.石油化工自动化，2008，44（02）：86－87.