响应变量缺失下线性回归模型的ERLS算法

刘力军

（大连民族学院理学院，辽宁大连 116605）

响应变量缺失下线性回归模型的ERLS算法

刘力军

（大连民族学院理学院，辽宁大连 116605）

针对线性回归模型，提出了一个新的期望递归最小二乘算法（Expectation Recursive Least Square，ERLS）。在响应变量数据存在部分缺失的条件下，ERLS取响应变量的期望值代替缺失值，基于该期望值与自变量数据，实现自适应的递归估计回归系数，避免了高维数据相关矩阵的求逆困难。ERLS算法充分利用了全部有效数据，实现了在线回归估计。数值实验结果表明，在观测数据存在野值时，通过引入非线性抑制函数，ERLS算法优于LS方法。

缺失数据;响应变量;递归最小二乘法（RLS）;线性回归

数据缺失现象在实际问题中经常发生，如可靠性寿命试验、遥外测数据提取、无线通信处理、模式识别等领域往往会出现大量缺失数据的现象［1－4］。EM算法最初由Dempster等［5］提出，主要用于计算后验分布的极大似然估计，如用于含缺失数据的线性与非线性模型的回归系数的估计问题［6－7］。针对响应变量存在随机缺失的线性模型的研究成为近期的热点［8－9］。

在自适应信号处理领域，如无线通信系统的信道估计中，一方面，数据样本的取得通常是通过传感器网络实时获取的，由于存储空间和传感器处理器运算速度的限制，传统的基于全部数据样本集进行似然估计的办法已无法应用，工程应用更希望获得运算复杂度低、只需较小存储需求的实时处理算法。这类算法通常只需要存储当前数据样本，无需存储全部数据集参与运算，因此这类实时处理算法被列为信号处理领域的典型研究课题［10］。另一方面，在自适应信号处理问题中，所处理的随机信号通常存在于非平稳环境中，这要求面向问题的算法要具有很好的适应性，在数据环境发生微小变化时，算法应具有较强的跟踪环境改变的能力。所有的物理采样系统，由于信道特性、环境噪声以及传感器设备的物理特性等因素，采样过程中得到的数据往往包含较大的随机误差，使得部分数据样本严重偏离目标真值，这些严重偏离目标真值的数据称为野值或者异常值［11］。实际应用表明，即使是包含少量的野值，对参数估计效果也会产生非常不利的影响，甚至导致算法结果明显地偏离系统状态真值［12］。

对于响应变量存在缺失的时变环境中，是否能够给出理想的实时自适应跟踪算法?对于线性回归问题模型，在响应数据随机缺失的前提条件下，在数据样本集存在野值时，能否得到更为稳健的自适应算法?本文针对上述问题提出了自适应ERLS算法，该算法基于EM框架，有效地解决了响应变量存在部分缺失时自变量数据如何有效利用问题;基于RLS增量式的递归算法结构，实现了递归估计极大化似然函数过程，通过引入非线性抑制函数，有效地解决了野值对算法的干扰;数值实验结果显示ERLS算法明显优于LS解。

1 响应数据缺失下的线性回归模型

设响应变量Y与自变量X1，X2，…Xm线性相关，n次观测数据D={（yi，xi1，xi2，…，xim）TєRm+1，（i=1，2，…，n）}满足以下多元线性回归模型:

假定Y随机缺失，即Y是否缺失只与X有关，而与Y无关，此时，若使用最小二乘解（4），一方面，矩阵求逆对于高维数据拟合会带来计算上的困难，另一方面，由于数据的部分缺失，只能抛弃与缺失数据相应的数据X，显见，单纯使用LS算法将会导致部分完整数据X无效，因此LS无法给出满意的解。

一个更合理的解决办法是基于不完全数据的统计处理方法——期望最大化算法（Expectation Maximization，EM），即依如下过程迭代计算θ（i） =（β（i），σ（i））（i=1，2，…）:

其中，观测数据集Dcomplete={Yobs，X}，Yobs为Y中观测到的数据，ymis为缺失分量Ymis的数据实现。在很宽的条件下，由EM算法产生的迭代序列{θ （i）}收敛到缺失数据线性回归问题的最优解［5］。

然而在一些实时处理领域，如信号处理和实时数据传输时，由于存储设备容量限制，通常获得整体是不经济的，甚至由于数据的流式传输，获得全部数据集也是不可能的。另一方面，在数据环境发生改变时，人们更希望所设计的算法能够自动适应这种环境的改变，从而给出自适应的最优解，而不是根据已经接收到的所有的样本集重新计算，因此它应当是增量式自适应的。为了有效解决野值数据问题，使算法应该能够依据数据特性做出自适应调整，抑制野值数据对算法的影响，本文给出了基于EM算法结构的期望递归最小二乘法（Expectation Recursive Least Square，ERLS）的线性回归算法，实现了对可用数据集似然函数的自适应递归估计。

2 期望递归最小二乘法（ERLS）

线性回归问题（2）的RLS算法［14］基于如下优化问题:

与封闭形式的最小二乘解（4）以及EM算法相比，RLS算法最大的特点是它特别适合于实时数据处理领域，因为每一次迭代它只需要最新的数据x（n）和yn，其算法复杂度为O（m2）。

在响应变量数据yi有部分缺失时，线性回归问题的RLS递归算法（9）不再适用。根据式（5），可知P（Y|X，β，δ）～Nm（Xβ，σ2Im），因此条件期望E（Y|X，β）=Xβ，从而E（yi|X）=xT（i）β，（i= 1，2，…，m）。在对应于自变量x（k）=（xk1，xk2，…，xkm）T的响应变量yk有缺失的情况下，一个自然的选择是以条件期望E（Yk|X，β）=xT（k）β代替yk，这类似于EM算法的E－step，同时，由于β未知，因此通过使用RLS算法，构造迭代序列β （i），进而计算E（yi|X，β（i））=xT（i）β（i），基于RLS结构的迭代过程，实现了M－step。

初始化:

应该注意到，ERLS算法的计算复杂度依然为O（m2），但有效地解决了缺失响应变量的不完全数据的线性回归问题，算法本质上是基于RLS的增量式递归算法。另外，在数据存在野值时，注意到误差|e（n）|=|dn－βT（n－1）x（n）|会变大，一种解决方案是取双曲正切sigmoid函数，即

其中，a＞0控制奇函数f（x）的形状，进而控制野值的影响范围。令e（n）=f（dn－βT（n－1）x （n）），数值实验结果表明，这一简单调整，可以有效抑制野值数据对回归算法的影响。另外，在yn丢失时，易见e（n）=0，即丢失y（n）并不参与运算，但是此时对应的x（n）依然参与运算，这从K（n）和P（n）的表达式可以看出。因此，ERLS算法充分地利用了所有可用的数据集。

3 数值实验

二元回归模型为

y=xTβ+ε=β1x1+β2x2+β3+ε，

式中，β=［β1，β2，β3］T=［1，2，3］T，x=［x1，x2，1］T，ε～N（0，0.01I2），随机生成1 000个样本点，取λ=0.99，δ=0.01，记ERLS算法给出的解为βERLS，LS算法给出的解为βLS，ERLS算法和LS算法给出的误差分别记为εERLS和εLS。通过如下四组试验分别测试算法的有效性、抗数据丢失性、抑制野值数据的韧性以及基于非线性变换的改进算法的有效性:

实验一响应变量无数据丢失，无野值数据

随机选择初值β（0）єR3，ERLS算法给出近似解βERLS=［1.0176，1.9876，3.0028］T，由方程（4）给出的LS解为βLS=［0.9877，1.9989，3.0097］T，二者的误差分别为εERLS=0.0218，εLS=0.0157。可以看到，对于无数据丢失、无异常值情况，二者均给出满意结果，此时LS解略优于ERLS解。无数据丢失时ERLS回归系数估计和误差曲线如图1和图2。可见，此时回归系数学习曲线和误差曲线都非常平滑，算法收敛速度快。

图1 无数据丢失时ERLS回归系数估计曲线

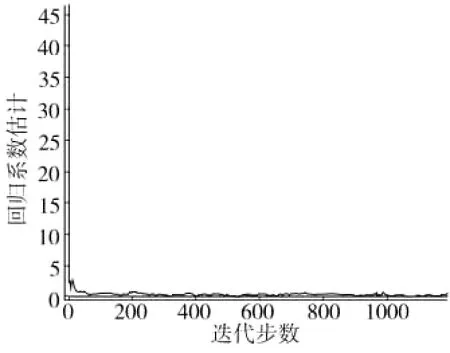
图2 无数据丢失时误差曲线

实验二80%响应变量数据丢失，无野值数据

随机选择初值β（0）єR3，ERLS算法给出近似解βERLS=［1.0085，2.0307，2.9688］T，由方程（4）给出的LS解为βLS=［1.0091，2.0462，2.9690］T，二者的误差分别为βERLS=0.0446，εLS=0.0564。回归系数和误差曲线如图3和图4。可以看到，对于有数据丢失、无异常值情况，二者均给出满意结果，由于ERLS基于EM算法结构，此时ERLS解略优于LS解。

图3 80%数据丢失时回归系数估计曲线

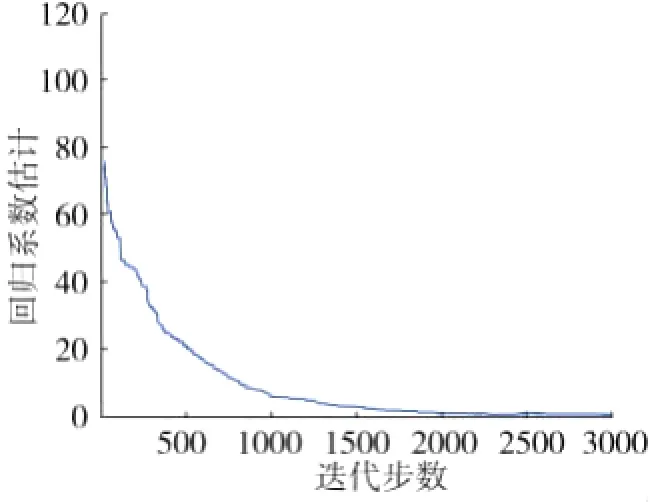
图4 80%数据丢失时误差曲线

实验三响应变量80%数据丢失，部分野值数据^d=d±100

ERLS算法给出近似解βERLS=［0.9785，1.9798，3.0303］T，由方程（4）给出的LS解为βLS=［0.6771，1.6003，3.27572］T，二者的误差分别为βERLS=0.0423，εLS=0.1608。部分野值数据时回归系数估计和误差曲线如图5和图6。可以看到，此时LS解给出解远远偏离真解，误差非常大，而ERLS算法依然给出相当满意的结果。回归系数学习曲线和误差曲线都非常平滑，但也由于野值数据影响出现了周期性的波动，可见异常数据对算法的影响非常大。

图5 部分野值数据时回归系数估计曲线

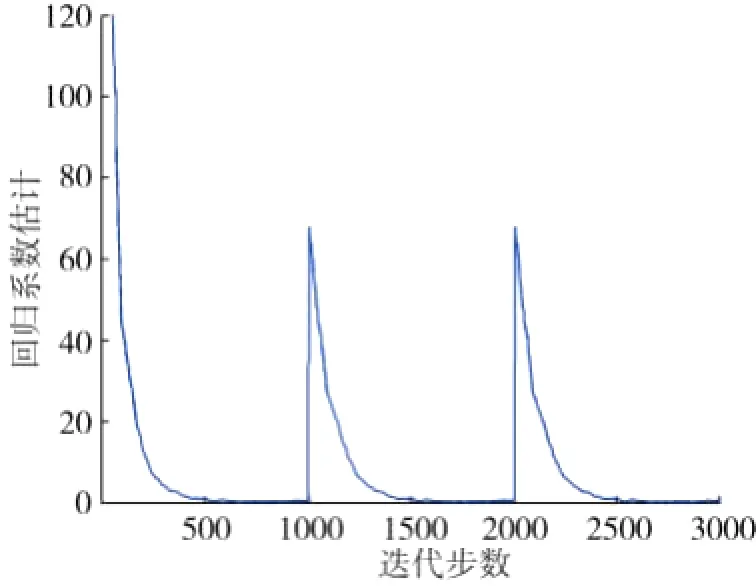
图6 部分野值数据时误差曲线

实验四取e（n）=f（dn－βT（n－1）x（n）），其中f（x）如方程（10）所示，且α=2，响应变量80 %数据丢失，部分野值数据^d=d±100。

ERLS算法给出近似解βERLS=［1.0036，1.9699，2.9736］T，由方程（4）给出的LS解为βLS=［－0.3302，0.2924，4.0065］T，二者的误差分别为βERLS=0.0402，εLS=2.3871。稳健ERLS算法回归系数估计和误差曲线如图7和图8。可以看到，此时LS解给出解远远偏离真解，误差非常大，而ERLS算法依然给出相当满意的结果，回归系数学习曲线和误差曲线都非常平滑，这正是由于sigmoid型函数对野值数据起到了积极抑制作用。

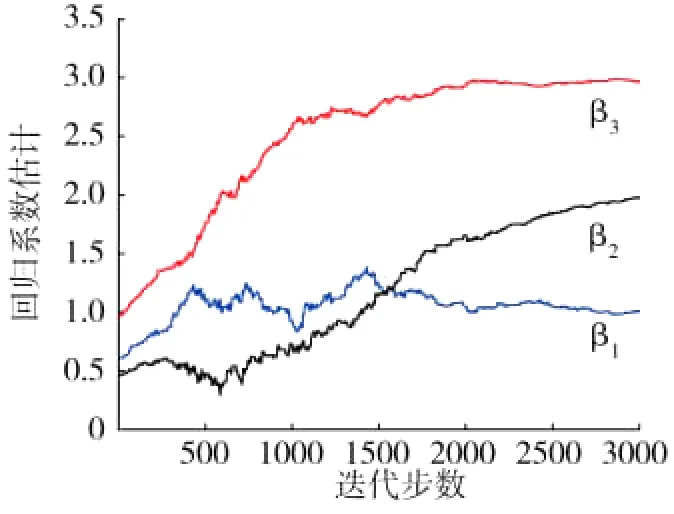
图7 稳健ERLS算法回归系数估计曲线

图8 稳健ERLS算法误差曲线

4 结论

本文提出了一个新的基于缺失数据模型ERLS算法，从分析结果可以看出，野值的存在使得LS解出现严重偏差，而使用本文提出的ERLS算法再结合非线性抑制函数，则可以自适应得到系统的最优解，算法回归曲线明显优于LS解。因此，ERLS算法能够有效地解决响应数据缺失问题和充分抑制动态数据中野值对滤波的影响。更为重要的是，ERLS算法通过对响应变量取期望值，对应自变量数据基于RLS算法迭代参与计算，从而充分地利用了全部有效数据集，且数值实验结果表明该方法简单有效。

［1］牟青，魏平.基于缺失数据模型的长码直扩信号的伪码估计［J］.电子学报，2010（10）:2365－2369.

［2］付惠娟，任美睿.无线传感器网络中缺失数据的估计［J］.计算机工程，2011，37（1）:90－92.

［3］沈奇，王池社.生物缺失数据处理的贝叶斯模型研究［J］.微电子学与计算机，2011，28（7）:110－112.

［4］刘鹏，雷蕾，张雪凤.缺失数据处理方法的比较研究［J］.计算机科学，2004（31）:155－174.

［5］DEMPSTER A P，LAIRD N M，RUBIN D B.Maximum likelihood from incomplete data via the em algorithm［J］.Journal of the Royal Statistical Society，B，1977，39 （1）:1－38.

［6］沈启霞，刘心声.含缺失数据线性模型回归系数的约束EM算法［J］.南京大学学报，2007，24（10）:122－131.

［7］周秀轻，王金德.随机删失数据非线性回归模型的最小一乘估计［J］.中国科学:A辑，2005，35（4）:387－403.

［8］杨宜平，薛留根，程维虎.响应变量存在缺失时部分线性模型的经验似然推断［J］.高校应用数学学报，2010，25（1）:43－52.

［9］赵丽棉，赵培信.响应变量随机缺失下变系数部分线性模型的借补经验似然推断［J］.应用数学，2011，24 （2）:215－219.

［10］张贤达.现代信号处理［M］.北京:清华大学出版社，2002.

［11］祝转民，秋宏兴，李济生，等.动态测量数据野值的辨识与剔除［J］.系统工程与电子技术，2004，26 （2）:147－149.

［12］李景熹，王宇，王树宗，等.观测值中野值的判别与处理方法仿真研究［J］.微计算机信息，2006，22:140－142.

［13］STRANG G.线性代数及其应用［M］.侯自新，译.天津:南开大学出版社，1990.

［14］TAMAL Bose.Digital signal and image processing［M］.New York:John Wieley＆Sous Inc，2004.

ERLS Algorithm for Linear Regression Model with Missing Response Variable

LIU Li－jun
（School of Science，Dalian Nationalities University，Dalian Liaoning 116605，China）

A novel Expectation Least Square（ERLS）algorithm is proposed for linear regression model.Under the condition that response is partly missing，ERLS uses expectation value of the response instead of the missing value.Based on the expectation value and the data of independent variable，ERLS adaptively estimates the regression coefficients，which avoids the difficulty of inversion operation to the correlation matrix of high－dimensional data.ERLS makes fully use of the available data and sovles the regression problem in an online manner.Numerical expriments show that，by introducing a nonlinear function of supression，ERLS is superior to LS solution under the existence of wild data points.

missing data;response variable;Recursive Least Square;linear regression

O212

A

1009－315X（2012）05－0469－05

2012－02－07;最后

2012－03－30

国家自然科学基金项目（61002039）;中央高校基本科研业务费专项资金资助项目（DC12010216）。

刘力军（1977－），男，满族，河北承德人，副教授，博士，主要从事神经网络算法研究。

（责任编辑 邹永红）