基于概率转移矩阵的氨基酸连接偏好性研究

张 堃， 唐旭清

（江南大学 理学院，江苏 无锡 214122）

基于概率转移矩阵的氨基酸连接偏好性研究

张 堃， 唐旭清＊

（江南大学 理学院，江苏 无锡 214122）

在Markov模型的基础上，提出了状态空间上合并映射的概念，以及合并过程下转移概率的计算方法。在已有氨基酸分类方法的基础上，结合Markov模型的概率转移矩阵，对氨基酸连接的偏好性进行了研究。结果表明：同一家族的蛋白质序列的氨基酸连接具有一定的偏好性，这种偏好性与氨基酸的分类有关，从而进一步说明了分类的科学性，同时这种偏好性对氨基酸序列的预测具有一定的作用。

氨基酸分类；合并映射；概率转移矩阵；偏好性

蛋白质空间结构的所有信息均隐藏在蛋白质的线性结构里面，确切的说，均隐藏在氨基酸序列里面。因此研究蛋白质序列就成了生物信息学研究领域的一个关键问题。目前已经发现的构成蛋白质分子链上的氨基酸类型有20种之多，直接研究蛋白质分子的折叠问题有困难，用分类法研究蛋白质结构，已有多种尝试，三联子串（氨基酸）依据其物理和化学特征，或者是依据氨基酸的空间结构特征来进行的不同的分类方式，目前的研究主要集中在几种简化的模型上。K.A.Dill等人［1］提出的HP模型将氨基酸分为4类。石秀凡及朱平等人［2］提出的拟氨基酸编码方法将氨基酸分为16类，杜晓林等人［3］应用信息聚类的方法将氨基酸分为5类，Soumalee Basu等人［4］在蛋白质序列的混沌游走表达一文中将20种氨基酸分为12类研究它们的分布情况。分类的依据和偏重不同，分类结果也不同。而这些分类事实上是一种状态合并的问题，即将具有一定关联的对象合并到一个类中，不同的分类对应着不同的粒度划分。在实际问题求解中，粒度划分是动态的，常用的氨基酸分类方法都是静态的。Markov过程是由其转移概率矩阵和初始概率分布构成的，其中的概率转移矩阵描述了其动态性。马氏链预测法［5］是通过对事物不同状态的初始概率及状态之间的转移概率的研究，预测事物的未来状态，在股票预测［6］，外汇收益预测［7］，基因预测［8－9］等方面都有广泛的应用。作者针对 Markov模型，结合氨基酸分类方法，对氨基酸连接的偏好性进行了研究，并以木聚糖酶家族［10］的蛋白质序列为例进行了分析。

1 材料与方法

1.1 数据来源

文中的数据来自Swiss－prot和Genebank中木聚糖酶家族的6条蛋白质序列O43097，P07528，P14768，P23030，P19127，P35811进行研究。另外文中的相关性分析是通过统计软件SPSS来完成的。

1.2 基于粒度下的Markov链

1.2.1 合并映射设 ｛X n，n≥0｝有限状态空间X上的齐次Markov链，其中X＝ ｛x1，x2，…，x N｝，如果将X中N个状态分类成M个状态分类成C＝｛C（1），C（2），…，C（M）｝，（M＜N）。对于给定的分类，建立了一个从X＝ ｛x1，x2，…，x N｝到Y＝ ｛y1，y2，…，y M｝的一个映射φ：∀x k∈X，∀y l∈Y，φ（x k）＝y1⇔k∈C（l），其中映射φ称为合并映射或压缩映射，C称为X的一个划分。同时这一过程｛Y n＝φ（X n）｝就成为相对于映射φ的合并过程［11］。

事实上，这里所给出的合并映射φ所起的作用就是给定了原始状态空间X上的一个商空间［12－13］Y＝ ［X］，以这个商空间作为状态空间（或观测空间）来研究原始马尔科夫链在这较粗状态空间（即X的商空间［X］下）的性质。在随机线性动力系统中，若给定输入 — 输出动力系统：x n＋1＝Ax n，y n＝Cx n，则在什么样的条件下，y n具有线性动力系统的性质，特别是当x n是随机变量X n的概率分布时，这个序列与Markov链相应，这里A是Markov链｛X n，n≥0｝的转移矩阵，而矩阵C就是压缩映射φ，即y n是随机变量φ（X n）的概率分布。1.2.2 合并过程的概率转移矩阵 若Markov链｛Xn，n≥0｝的状态空间为I＝ ｛1，2，…，N｝，设φ为从I到集合Y＝ ｛y1，y2，…，y M｝（M＜N）的合并映射，即，∀k∈I，∀y l∈Y，φ（k）＝y l⇔k∈φ－1（y l），此时称Y为I的商空间，｛Y n＝φ（Xn）｝就成为相对于映射φ的合并过程。若｛Xn，n≥0｝的初始概率向量为X0＝ （π1，π2，…，πN），则

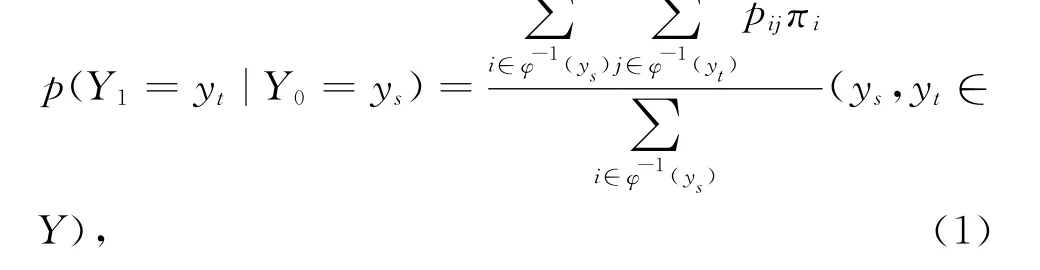
令ast＝P（Y1＝y t｜Y0＝ys），矩阵A＝（ast）s，t∈Y为合并过程｛Y n＝φ（X n）｝在状态空间Y上的转移矩阵。

1.2.3 应用举例 对于一条由610个氨基酸构成的蛋白质序列来说，作如下假设，设610个位置为610个时刻，｛A，F，I，L，M，P，V，W，Y，T，S，Q，N，G，C，H，K，R，D，E｝为由20种氨基酸构成的状态空间，该状态空间对应于一个号码集合I＝ ｛1，2，…，20｝，令X（n）表示氨基酸n后面所连接的氨基酸种类，显然X（n）是一个随机变量，｛X（n），n＝1，2，…，20｝是一个离散参数的随机过程，并且每个氨基酸后面所连接氨基酸与前面的状态无关，只与蛋白质序列本身有关，氨基酸i与氨基酸j连接的概率与i所在的时刻无关，因此氨基酸之间的连接过程可以看成是一个Markov过程。于是Markov预测模型可以定义为一个三元组（X，P，π），其中X为20种氨基酸构成的状态空间，P为一阶概率转移矩阵，π为初始分布。定义X到Y1＝ ｛y1，y2，y3，y4，y5，y6，y7，y8，y9，y10，y11，y12｝上 的 合 并 映 射φ1，X到Y2＝｛y1，y2，y3，y4｝上的合并映射φ2。

φ1（x i）＝y i，x i∈ ｛｛C｝，｛H｝，｛N｝，｛P｝，｛Q｝，｛W｝，｛Y，F｝，｛A，G｝，｛S，T｝，｛K，R｝，｛D，E｝，｛I，L，V，M｝｝

φ2（x j）＝y i，x j∈ ｛｛A，F，I，L，M，P，V，W｝，｛Y，T，S，Q，N，G，C｝，｛H，K，R｝，｛D，E｝｝

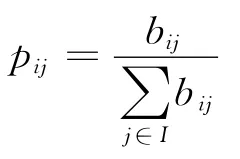
这样我们就得到了6个初始概率和6个20×20的一阶概率转移矩阵，通过合并映射φ1，φ2和公式（1）可得合并后的12×12，4×4转移矩阵。

2 结果与分析

2.1 相关性分析

衡量事物之间或变量之间线性相关程度的强弱，并用适当的统计指标表示出来，这个过程就是相关分析［14］。它是研究变量间密切程度的一种常用统计方法。主要分为线性相关分析，偏相关分析，距离相关分析3类，作者主要研究线性相关分析。线性相关分析是研究两个变量间线性关系的程度，相关系数是描述这种线性关系程度和方向的统计量，用r来描述，若变量Y与X间是函数关系，则r＝1或r＝－1；如果变量Y与X间是统计关系，则－1＜r＜1，一般地，｜r｜＞0.95存在显著性相关；｜r｜＞0.8高度相关；0.5≤｜r｜＜0.8中度相关；0.3≤｜r｜＜0.5低度相关；｜r｜＜0.3关系极弱，认为不相关。

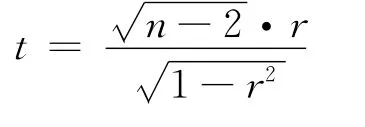
在1.2.3节中得到了6条序列的12×12和4×4概率转移矩阵，以序列O43097为例，令α＝（α1T，…，α2T，α12T）T，其中αi表示该序列所对应的12×12概率转移矩阵中的第i列，则α为含144个分量的列向量，同样的方法可以得到其他五条序列的所对应的列向量，利用SPSS软件对这六个列向量进行了相关性分析，结果如表2.1所示。按照同样的步骤可以得到4×4概率转移矩阵所对应的列向量，相关性分析如表2.2所示。

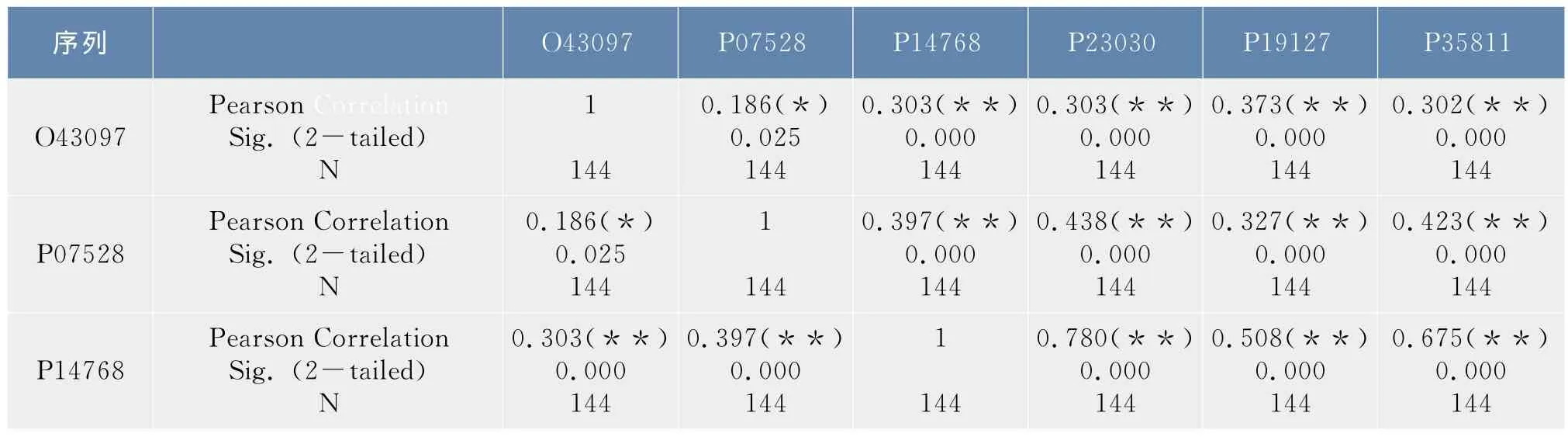
表1 合并映射φ1下6条序列概率转移矩阵的相关性分析Tab.1 Correlation analysis of the probability transition matrix of the six sequences under the lumping mapφ1

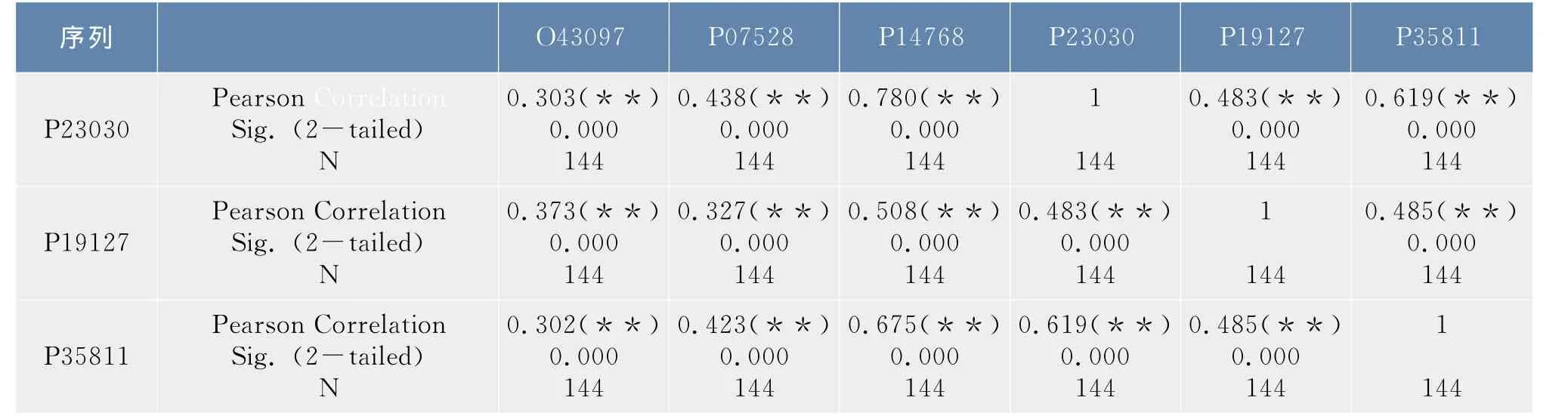
续表1

表2 合并映射φ2下6条序列概率转移矩阵的相关性分析Tab.2 Correlation analysis of the probability transition matrix of the six sequences under the lumping mapφ2

在上述相关性分析表中，Pearson Correlation表示的是相关系数r，Sig.表示的是显著性概率，N表示的是向量中分量的个数。

从表1中可以看出除序列O43097和序列P07528之间的显著性概率值介于0.01和0.05之间外，其他序列间的显著性概率均小于0.01，从表2中可以看出，所有序列之间的显著性概率值都小于0.01，均高度相关，而且相关系数均大于0.7，相关性都非常显著。这说明在映射φ1，φ2下6条序列都是高度相关的，因此可以将6条序列合并处理，得到了合并序列所对应的20×20概率转移矩阵及初始分布。

2.2 合并后的概率转移矩阵

根据1.1节得到的数据，包括木聚糖酶家族的6条蛋白质序列，按照1.2.3节定义的合并映射以及公式（1），得到了2.1节中合并序列在φ1，φ2下的概率转移矩阵，如表3和表4所示。矩阵中的元素表示两个氨基酸类之间的连接概率，例如，0.025 641表示的是氨基酸C后面连接的氨基酸为H的概率是0.025 641，0.307 692表示的是氨基酸C后面连接的氨基酸为A或者G的概率为0.307 692。

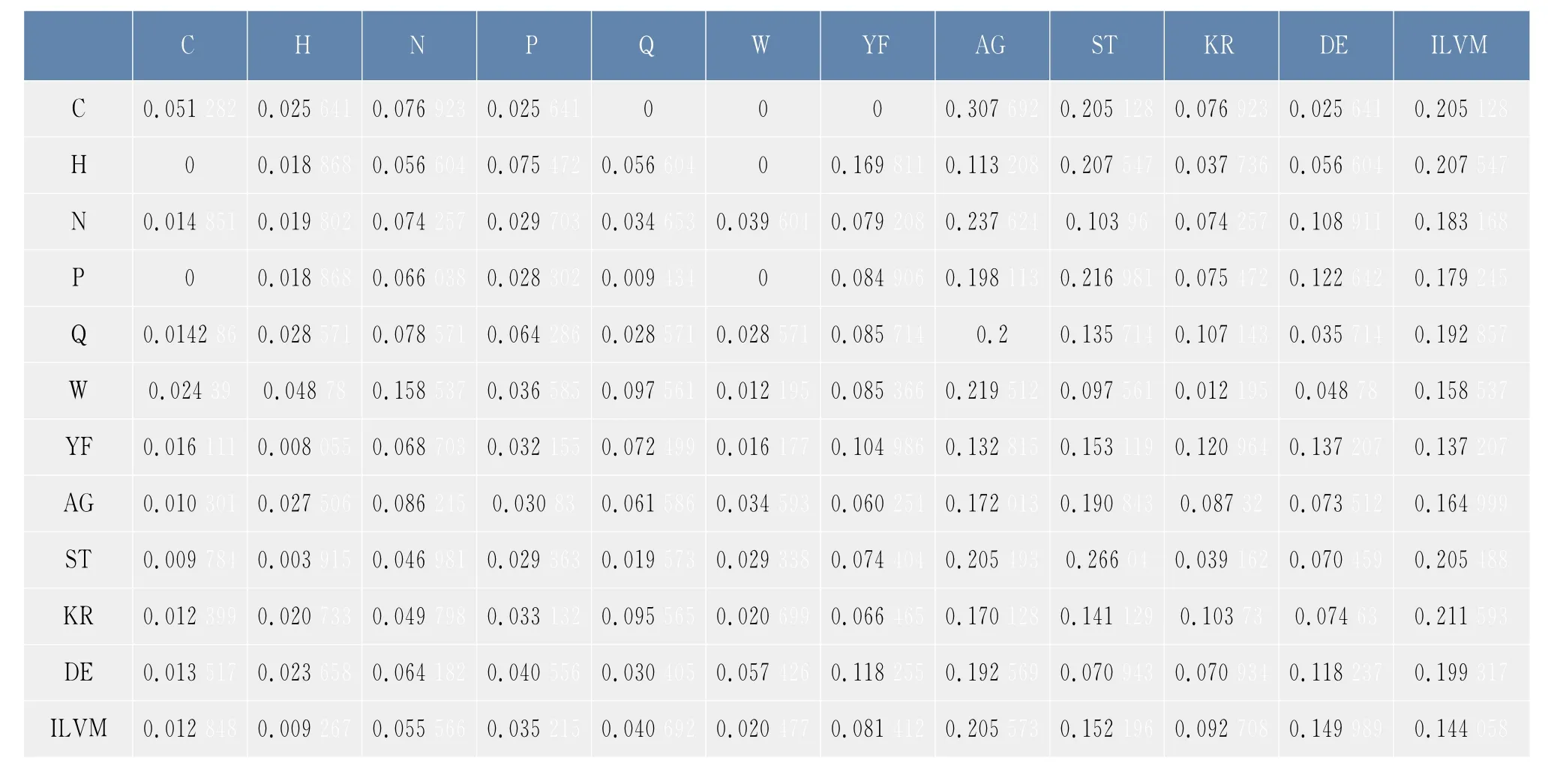
表3 合并序列在φ1下的概率转移矩阵Tab.3 Probability transition matrix of the lumped sequence under the lumping mapφ3

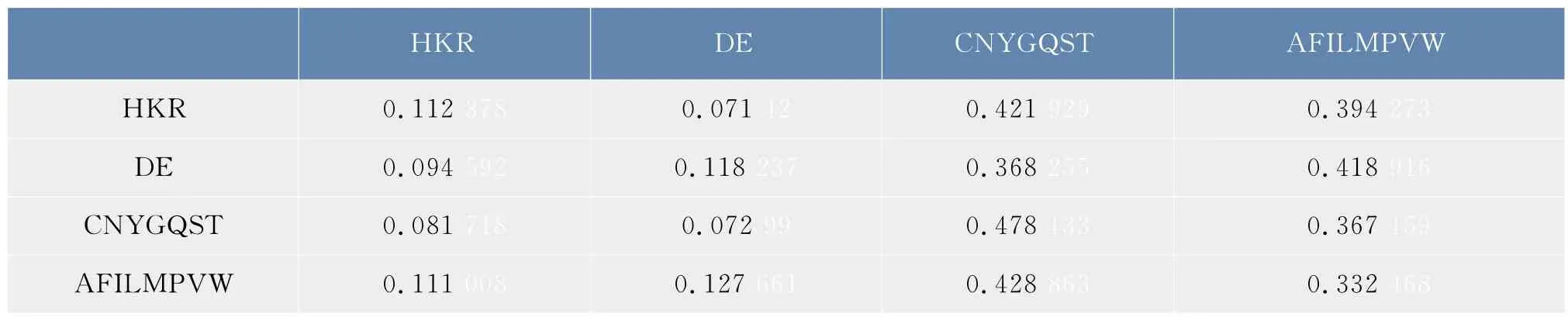
表4 合并序列在φ2下概率转移矩阵Tab.4 Probability transition matrix of the lumped sequence under the lumping mapφ2

观察表3和表4，可以发现氨基酸之间的连接具有一定的偏好性，通过比较两种分类方式的转移概率，发现该家族的蛋白质序列均偏好使用氨基酸A，G，S，T，I，L，V，M 均不偏好使用氨基酸 H，K，R，D，E等，同时还发现氨基酸之间连接的偏好性与氨基酸的分类有关，极性不带电荷R基团氨基酸，即｛C，N，Y，G，Q，S，T｝，后面连接｛C，N，Y，G，Q，S，T｝的概率接近二分之一，而与带正电荷的氨基酸｛H，K，R｝及带负电荷的氨基酸｛D，E｝相连的概率则非常小。

3 结语

氨基酸之间的连接并非随机的均匀的，而是具有一定偏好性的，作者在Markov模型的基础上，结合已有氨基酸的分类方法，提出了一种基于概率转移矩阵的氨基酸连接偏好性的研究方法，并以木聚糖酶家族的蛋白质序列为例进行了系统的阐述。研究表明，氨基酸之间的连接具有一定的偏好性，这种偏好性与氨基酸的分类密切相关，同时与密码子使用的偏好性有关。对于木聚糖酶家族而言，极性不带电荷R基团氨基酸，后面连接极性不带电荷R基团氨基酸的概率接近二分之一，而与带正电荷的氨基酸及带负电荷的氨基酸相连的概率则非常小。这些氨基酸之间连接的偏好性研究对于蛋白质结构预测具有一定的指导意义，一方面可以进一步说明氨基酸分类方式的科学性，同时对蛋白质氨基酸序列的预测有一定的作用，相对于实验室测序、拼装这样预测节省人力物力财力，这将是下一步研究的主要内容。

（References）：

［1］Lau K F，Dill K A.A lattice statistical mechanics model of the conformation and sequence spaces of proteins［J］.Macromolecules，1989，22：3986.

［2］朱平，高雷，徐振源.基于拟氨基酸编码方法下的同义密码子的偏好性仍与结合强度密切相关［J］.物理学报，2009，6：714－719.

ZHU Ping，GAO Lei，XU Zhen－yuan.The usage degree of synonymous codon is close correlated with the strength of combination based on the quasi－amino acid coding［J］.Acta Physica Sinica，2009，6：714－719.（in Chinese）

［3］杜晓林，郝玉兰.氨基酸数量化分类的研究初探［J］.生物数学学报，1994，9（5）：105－107.

DU Xiao－lin，HAO Yu－lan.Preliminary study on the quantified Classification of amino acid［J］.Journal of Biomathematiccs，1994，9（5）：105－107.（in Chinese）

［4］Soumalee B，Archana P，Chitra D，et al.Chaos game representation of proteins［J］.Journal of Molecular Graphics and Modelling，1997，15：279－289.

［5］Huseyin P，Wenliang D，Sahin R，et al.Private predictions on hidden markov models［J］.Artifical Intelligence Review，2010，34（1）：153－172.

［6］Md.Rafiul H，Baikunth N，Michael K.A fusion model of HMM，ANN and GA for stock market forecasting［J］.Expert Systems with Applications，2007，33：171－180.

［7］Dueker M，Christopher J.Neely.Can Markov switching models predict excess foreign exchange returns？［J］.Journal of Banking ＆ Finance，2007，31（2）：279－296.

［8］马宝山，朱义胜.基于隐马尔科夫模型的基因预测算法［J］.大连海事大学学报，2008，34（4）：41－44.

MA Bao－shan，ZHU Yi－sheng.Gene－prediction algorithm based on hidden Markov model［J］.Journal of Dalian Maritime University，2008，34（4）：41－44.（in Chinese）

［9］张新生，王梓坤.生命遗传信息中若干数学问题［J］.科学通报，2000，45（2）：113－119.

ZHANG Xin－sheng，WANG Zi－kun.Several methematical problems of genetic information of life［J］.Chinese Science Bulletin，2000，45（2）：113－119.（in Chinese）

［10］刘亮伟，杨海玉，胡瑜，等.F／10木聚糖酶研究进展［J］.食品与生物技术学报，2009，6：727－732.

LIU Liang－wei，YANG Hai－yu，HU Yu，et al.A review of F／10 xylanase［J］.Journal of Food Science and Biotechnology，2009，6：727－732.（in Chinese）

［11］Leonid G，James L.Markov property for a function of a markov chain：A linear algebra approach［J］.Linear Algebra and its Applications，2005，404：85－117.

［12］张铃，张钹.问题求解理论与应用：商空间粒度计算理论及应用［M］.北京：清华大学出版社，2007.

［13］Tang X Q，Zhu P，Cheng J X.The structural clustering and analysis of metric based on granular space［J］.Pattern Recognition，2010，43：3768－3786.

［14］朱建平，殷瑞飞.spss在统计分析中的应用［M］.北京：清华大学出版社，2007.

Research on the Connection Bias of Amino Acids Based on Probability Transition Matrix

ZH ANGKun，TANGXu－qing＊

（School of Science，Jiangnan University，Wuxi 214122，China）

In this manuscript，a novel concept of lumping map and a computing method of the transition probability in lumped process were suggested based on Markov model，to investigate the connection bias of amino acids.The results demonstrated that the connection of amino acids had a particular preference which was related to the classification of amino acids，and further verified the scientific of the classification of amino acids.At the same time，the preference would give some help for the prediction of amino acids sequence.

classification of amino acids，lumping map，probability transition matrix，bias

Q 71；O 29

A

1673－1689（2012）01－0106－06

2011－01－03

＊

唐旭清（1963－），男，安徽望江人，工学博士，教授，主要从事智能计算，生态系统建模与仿真及生物信息学研究。Email：txq5139＠jiangnan.edu.cn