关于高等代数中几何实例的初步探讨
2012-01-11黄娟霞
黄娟霞
(陇南师范高等专科学校 数学系,甘肃 成县 742500)
高等代数是高校数学专业的一门基础课程,其概念繁多且抽象难懂.因此,概念教学成为整个高等代数教学的灵魂.其实,之所以大家感觉高等代数的概念抽象是因为这些概念在实际的生活中得不到印证.经过笔者的教学经验,对于高等代数中一些抽象难懂及易于混淆的概念,如果能够找到恰当的几何实例,将概念的抽象性和具体性统一起来,那么在教与学的过程中会收到事半功倍的效果.
1 关于线性变换概念的几何实例
线性变换是高等代数中比较抽象的概念.任何科学概念的形成,一方面是对感性具体进行抽象的结果;另一方面是不断深入事物的本质,具体把握对象的矛盾运动的过程.因此,对于这种类型的概念,如果能够给出恰当的几何实例将会让教学有意外的收获.
定义1 设σ是F上向量空间V的一个变换. 若对于V中任意向量α,β及F中任意数k,都有
σ(α+β)=σ(α)+σ(β);
σ(kα)=kσ(α)
则称σ是V的一个线性变换.
例1 设{ε1,ε2,ε3}是V3的标准基,对V3的任一向量α=a1ε1+a2ε2+a3ε3,β=b1ε1+b2ε2+b3ε3,规定σ(α)=a1ε1+a2ε2+0ε3.下面验证映射σ是V3的线性变换.
解对V3中任意向量α=a1ε1+a2ε2+a3ε3,β=b1ε1+b2ε2+b3ε3及任意实数k,
因为
σ(α+β)=
σ(aε1+a2ε2+a3ε3+b1ε1+b2ε2+b3ε3)=
σ((a1+b1)ε1+(a2+b2)ε2+(a3+b3)ε3)=
(a1+b1)ε1+(a2+b2)ε2+0ε3=
(a1ε1+a2ε2+0ε3)+(b1ε1+b2ε2+0ε3)=
σ(α)+σ(β)
σ(kα)=σ(k(a1ε1+a2ε2+a3ε3))=
σ(ka1ε1+ka2ε2+ka3ε3)=
ka1ε1+ka2ε2+0ε3=
k(a1ε1+a2ε2+0ε3)=
kσ(α)
所以,σ是V3的线性变换.σ的几何意义是把V3的向量α投影到由ε1,ε2所决定的oxy平面上去.
2 关于易混淆的概念的几何实例
2.1 子空间的和与直和
定义2 设W1,W2是向量空间V的两个子空间,称 {α|α∈W1且α∈W2}为W1与W2的交,记作W1∩W2.称{α1+α2|α1∈W1,α2∈W2}为W1与W2的和,记作W1+W2.
定义3 设W1,W2是向量空间V的两个子空间,W=W1+W2.若W1∩W2={0},则称W是W1与W2的直和,记作W=W1⨁W2.
向量空间的和与直和这两个概念的区别关键在于有没有“W1∩W2={0}”,如果有,则是子空间的直和,如果没有,则是子空间的和.下面通过几何实例对这两个概念进行区分.
例2 在三维向量空间V3中,W1,W2是它的两个子空间.
(1)W1={在xoy平面内从原点出发的所有向量},W2={在yoz平面内从原点发出的所有向量}.
设任意α1∈W1,α2∈W2,则α1+α2=α3∈V3,故W1+W2=W3,而W1∩W2={从原点出发沿y轴方向或反方向的所有向量}≠{0}.因此,W1⨁W2≠V3(见图1).
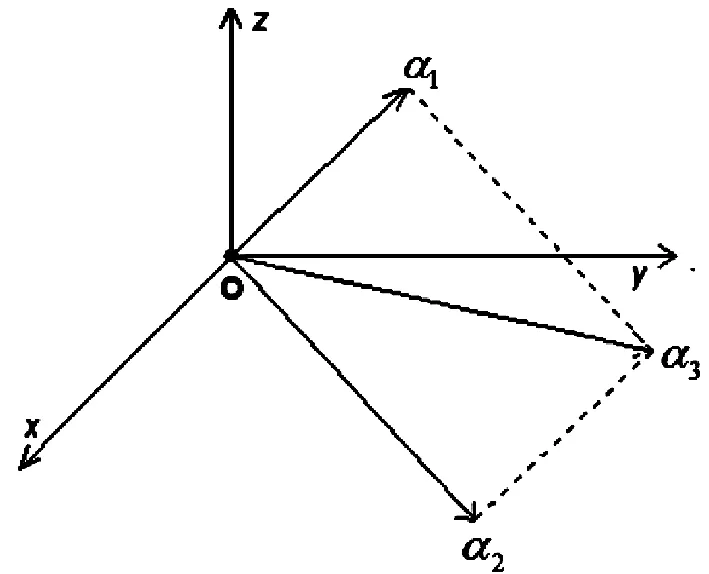
图1 两个子空间的和
(2)W1={从原点出发沿x轴方向或反方向的所有向量},W2={在yoz平面内从原点出发的所有向量}.
设任意α1∈W1,α2∈W2,则α1+α2=α3∈V3,故,W1+W2=V3,且W1∩W2={0}.因此,W1⨁W2=V3(见图2).
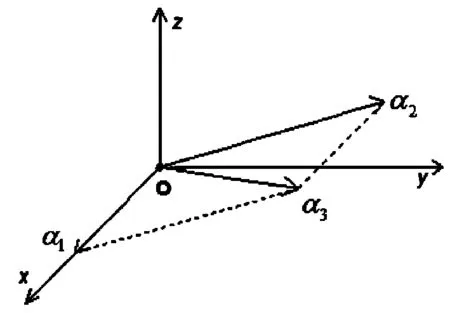
图2 两个子空间的直和
2.2 关于欧氏空间的正交变换与对称变换的几何实例
定义4 欧氏空间V的线性变换σ称为正交变换,如果它保持任意两个向量的内积不变,即对任意α,β∈V,有<σ(α),σ(β) >=<α,β>.
定义5α是欧氏空间V的一个线性变换.如果对V中任意两个向量α,β,都有<σ(α),β)>=<α,σ(β)> ,那么称σ为一个对称变换.
正交变换和对称变换是两个相类似的概念,这种概念往往容易混淆,下面通过具体的几何实例对这两个概念的异同进行比较.
例3 在欧氏空间V2中,σ是把V2中任意向量α都沿逆时针方向旋转θ角的变换,则σ是正交变换.

图3 正交变换
例4 在欧氏空间R2中,σ是把R2中任意向量α作x轴的正投影,则σ是对称变换.

σ(β)=(c,0) σ(α)=(a,0)
参考文献:
[1]北京大学数学系.高等代数[M].北京:高等教育出版社,2003.
[2]刘仲奎,杨永保,等.高等代数[M].北京:高等教育出版社,2003.
[3]黎伯堂,刘桂真.高等代数解题技巧与方法[M].山东:山东科学技术出版社,2003.
[4]李硕,刘福国.集合理论在高等代数课程教学中的特殊作用刍议[J].昌吉学院学报,2006(3):117-119.
