电感耦合等离子体原子发射光谱法测定铜合金中锆量的不确定度评定

雷宏田

（中国第一汽车股份有限公司技术中心，长春 130011）

电感耦合等离子体原子发射光谱法测定铜合金中锆量的不确定度评定

雷宏田

（中国第一汽车股份有限公司技术中心，长春 130011）

讨论了采用电感耦合等离子体发射光谱法测定铜合金中锆量分析结果不确定度产生的原因。建立了数学模型，对测量重复性，标准溶液，标准曲线变动，试液体积，试样称量，数字修约等引起的不确定分量进行评定，计算了合成标准不确定度和扩展不确定度，并给出铜合金中锆量测定结果的报告。评定结果表明：测量重复性，标准曲线线性回归引起的不确定度对总不确定度影响最大。所以在测定中应进行多次平行测定，特别注意标准曲线的校正和绘制校准曲线所用标准样品的选择。

电感耦合等离子体原子发射光谱法；铜合金；锆；不确定度

1 前言

测量不确定度［1－2］是指表征合理的赋予被测量值的分散性，是与测定结果相联系的参数。不确定度的评定方法有多种，按评定方法的不同分为A类和B类。前者由观测系列统计分析所做评定，后者由不同于对观测系列统计分析所做评定。二者并没有实质的差异，都基于概率分布，都可用方差或标准偏差来表示。

测量不确定度评定已有很多报道［3－5］。依据相关技术规范，用GB／T 5121.27—2008铜及铜合金化学分析法电感耦合等离子体原子发射光谱法进行测定，建立了数学模型，分析了其测定结果不确定度产生的原因，进行了分量评定，计算了合成标准不确定度和扩展不确定度，最后完成不确定度报告，从而获得较为完整的定量分析报告。

2 实验部分

2.1 主要试剂和仪器

Optima－4300DV双向观测全谱直读等离子体原子发射光谱仪（Perkin Elmer）。

锆标准储备溶液（国家钢铁材料测试中心，钢铁研究总院）（1000mg／L），盐酸（1＋9）介质；

锆标准溶液（100mg／L）：移取10.00mL锆标准储备溶液于100mL容量瓶中，以水稀释至刻度，混匀；

饱和硼酸溶液：称取70g硼酸于1L热水中，溶解后冷却至室温；

氢氟酸、硝酸、盐酸均为分析纯；

混合酸：盐酸－硝酸－水（1＋3＋4）混合溶液。

2.2 仪器工作条件

高频发生器功率：1.2kW，氩气纯度不小于99.99%，冷却气流量15L／min，载气流量0.8L／min，辅助气流量0.2L／min，试液提升量1.5L／min，观测高度15mm，波长399.19nm。

2.3 实验方法

2.3.1 试样的溶解

准确称取0.1000g试样置于100mL聚四氟乙烯烧杯中，加入混合酸10mL，2滴氢氟酸，加热溶解。待试样溶解完全后，加入饱和硼酸溶液5mL，混匀，冷却，移入100mL塑料容量瓶中，以水稀释至刻度，混匀。

2.3.2 标准曲线绘制

移取锆标准溶液0、1.00、2.00、3.00、5.00mL于一组100mL容量瓶中，分别加入混合酸10mL，用水稀释至刻度，混匀。在仪器工作条件下测量其光谱强度。以锆的质量浓度对相应的光谱强度绘制标准曲线。在标准曲线上查取试样溶液中锆的含量，计算试样中锆的质量分数。

3 不确定度的评定

3.1 数学模型的建立

元素含量与输入量的函数关系如下：

式中：wZr为试样中元素的质量百分数（%）；m为试样的质量（g）；c为工作曲线上查得的试液中元素的质量浓度（mg／L）；V为试液总体积（mL）；I为光谱强度；a为截距；b为斜率。

3.2 不确定度来源分析

由随机效应引起的不确定度来自于测量重复性，标准曲线线性回归，这类不确定度分量采用A类方法进行评定；由系统效应引起的不确定度来自于标准溶液、标准溶液稀释、分取、定容、称量误差、测量结果的数字修约等，这类不确定度分量采用B类方法评定。

3.2.1 测量重复性引入的标准不确定度u（s）

按试验方法对锆青铜标样（BY 1958－2）（锆的质量分数：0.43%）进行2次测定，测定结果分别为0.44%和0.45%，平均值为0.44%。属有限的重复性，可引用条件下操作的测试数据来评定其重复性不确定度。按GB／T 5121.27—2008铜及铜合金化学分析法 电感耦合等离子体原子发射光谱法，锆的重复性限r＝0.034%，s＝r／2.83＝0.012%。

3.2.2 标准曲线引入的不确定度u（ρ）

3.2.2.1 锆标准储备溶液的不确定度u（ρ）1

已知锆标准储备溶液（GSB G 62033－90）的质量浓度是1000mg／L，扩展不确定度U＝0.4%。

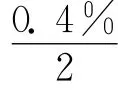
3.2.2.2 配置锆标准溶液（100mg／L）的不确定度u（ρ）2

1）容量瓶校准引入的不确定度

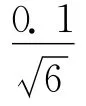
2）移取体积的标准不确定度

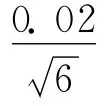
3）合成锆标准溶液（100mg／L）的相对不确定度u（ρ）2

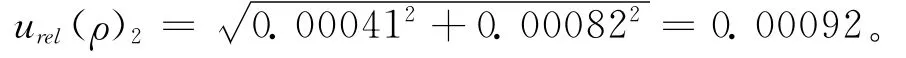
3.2.2.3 分取标准溶液体积的不确定度u（ρ）3

绘制标准曲线时，用一支5.00mL刻度移液管分别移取锆标准溶液0.00、1.00，2.00、3.00、5.00mL于 100mL容量瓶中，根据GB／T 12807—1991允许差要求，其体积误差分别为0、±0.008、±0.012、±0.012、± 0.015mL，按三角形分布处理，则相应的标准不确定度为0、0.0033、0.0049、0.0049、0.0061mL，按均方根计算，分取标准溶液体积误差引起溶液浓度的相对标准不确定度urel（ρ）3：

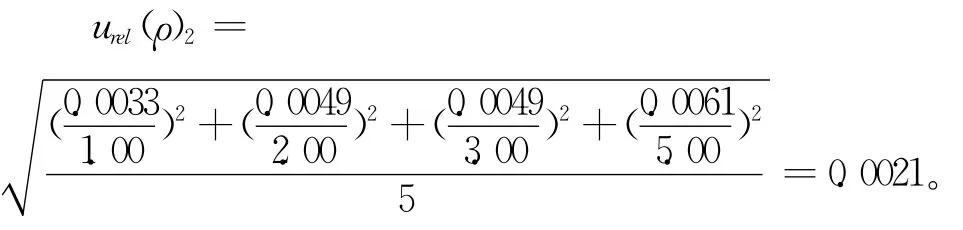
合成标准曲线用标准溶液引起的相对不确定度：

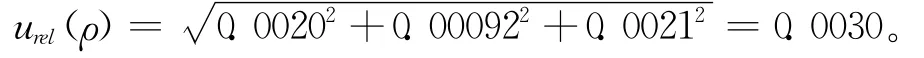
3.2.3 标准曲线变动性的不确定度u（r）

将标准溶液进行测定，结果见表1。

表1 校准曲线参数统计Table 1 Statistical parameters of the calibration curves

按表1的测试数据，用最小二乘法拟合线性回归方程，标准曲线线性回归的结果：

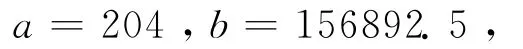
拟合的标准曲线方程为：

标准曲线的标准偏差

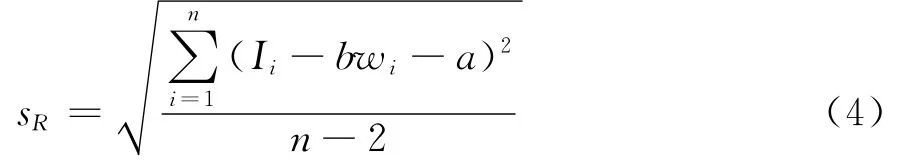
由标准曲线线性回归引入的标准曲线系数的标准不确定度：

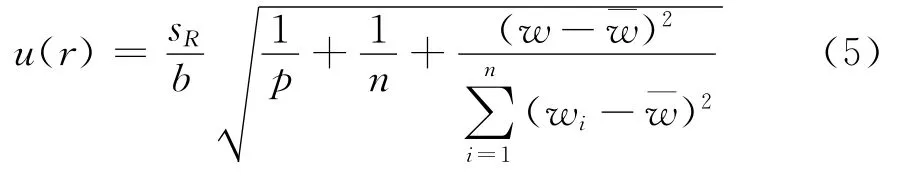
式中：a、b为标准曲线线性回归系数；p为试样测试的次数；n为测试标准溶液的次数；w为测试试样中元素的质量分数（%）；¯w为不同标准溶液的质量分数的平均值（%）；wi为第i个标准溶液的质量分数（%）；I为第i个标准溶液的光谱强度。

n＝5，由公式（4）得s＝709；

p＝2，由公式（5）得u（r）＝0.0073%，urel（r）＝0.017

3.2.4 试液体积引入的不确定度

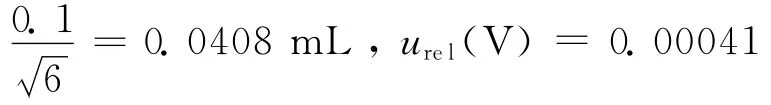
3.2.5 试样称量误差引入的不确定度u（m）

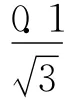
3.2.6 电感耦合等离子体原子发射光谱读数修约引入的不确定度urel（X）

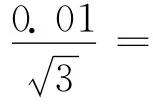
3.3 合成不确定度的评定

元素值和不确定度分量汇总，见表2。

各分量互不相关，按方和根计算合成相对不确定度，则

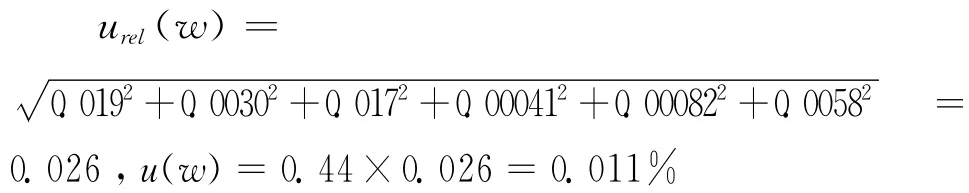
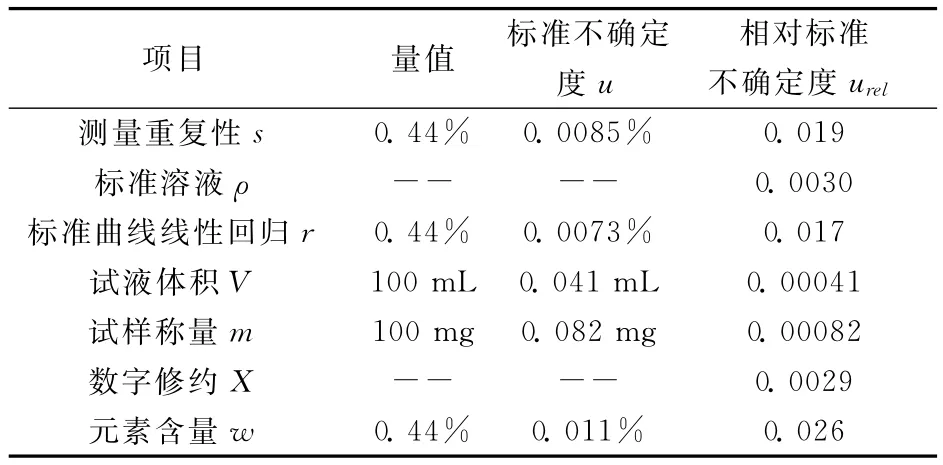
表2 元素量值及不确定度分量汇总Table 2 Summary of the element values and the uncertainty components

3.4 扩展不确定度的评定

在95%的置信概率下，kp＝2，U＝0.011× 2＝0.022%。

3.5 不确定度报告

电感耦合等离子体原子发射光谱法测定铜合金中锆的测量结果为w＝（0.44±0.022）%。

4 结论

从评定过程看出，测量重复性，标准曲线线性回归对不确定度影响最大。因此，测试试样时，应多重复次数；应增加标准溶液的测量次数，设置标准曲线时尽量使样品浓度位于标准曲线的中间，此外准确配置和分取标准溶液，严格按分析步骤操作，使用稳定性高的设备仪器，注意测量技巧等都是可以有效减小测量不确定度的措施。

［1］国家标准物质研究中心.JJF 1135－2005化学分析测量不确定评定［S］.北京：中国计量出版社，2005：4－9.

［2］中国计量科学院.JJF 1059—1999测量不确定度评定与表示［S］.北京：中国计量出版社，1999：10－20.

［3］曹宏燕.分析测试中测量不确定度及评定［J］.冶金分析，2006，26（2）：82－83.

［4］康志清，宋祖峰，穆新玉.等.X射线荧光光谱法测定萤石中CaF2含量不确定度的评定［J］.冶金分析，2010，30（11）：74－78.

［5］韦新红，魏雅娟，陈永欣，等.电感耦合等离子体质谱（ICP－MS）法测定高纯氧化铟中铜含量的不确定度评定［J］.中国无机分析化学，2011，1（2）：50－53.

Uncertainty Evaluation on Determination of Zirconium in Copper Alloy by Inductively Coupled Plasma Atomic Emission Spectrometry

LEI Hongtian
（ChinaFAWcroupCo.，Ltd.R＆Dcenter，Changchun，Jilin130011，China）

The causes for uncertainty for quantitative determination of zirconium in copperalloy by inductively coupled plasma atomic emission spectrometry（ICP－AES）were discussed.A mathematical model was established.The uncertainty caused by the measurement repeatability，standard solution，standard curve linear regression，test solution volume，sample weighing and rounding number，etc.were evaluated.The combined standard uncertainty and expanded uncertainty were calculated and the content of zirconium in copper alloys was reported.The evaluation results showed that：measurement repeatability and the standard curve linear regression uncertainty made the greatest contribution to the overall uncertainty.Therefore，the best quantitative analysis should be conducted by parallel repetitive measurements.Furthermore，special attention should be paid to the correction of a standard curve and the selection of standard samples.

inductively coupled plasma atomic emission spectrometry；copper alloy；zirconium；uncertainty

O657.31；TH744.11

A

2095－1035（2012）01－0070－04

10.3969／j.issn.2095－1035.2012.01.0017

2011－11－10

2011－12－11

雷宏田，女，高级工程师，主要从事汽车用材料化学与光谱分析及研究工作。E－mail：leihongtian＠rdc.faw.com.cn。