TCM好码在空时编码中的应用

吴军，孙涛，钟阳万，吴小波

（江西理工大学信息工程学院，江西赣州341000）

TCM好码在空时编码中的应用

吴军，孙涛，钟阳万，吴小波

（江西理工大学信息工程学院，江西赣州341000）

网格编码将调制器和编码器看成一个整体综合设计，使得编码后的信号序列之间有最大的欧式自由距离，它可以在不需要扩张带宽或提高功率的情况下取得更好的性能.文中介绍了网格编码（TCM）好码的简化搜索算法，并将搜索到的最小TCM好码应用于空时编码中，对空时分组编码（STBC）和级联了最小TCM好码的STBC在相同的符号发送功率、信息速率和频带利用率条件下的误比特率（BER）进行比较，验证了最小TCM好码和级联码的优良性能.

网格编码；空时分组编码；级联码

0 引言

所有的错误控制编码技术中，都是以某种方式在信息比特中加入额外的比特，因此比特错误率的改善是以增加带宽为代价的.在传统的数字传输系统中为了提高系统的性能，一般有两种方法：提高信号功率或者增加传输带宽.由Ungerboeck提出的网格编码调制理论（TCM，Trellis Coded Modulation）将调制器和编码器看成一个整体综合设计，这个方案在高斯白噪声（AWGN）信道下不需要带宽扩张或额外功率可以在相同信息速率下可获得3～6 dB的功率增益[1-2].

在考虑译码复杂度的基础上，空时编码设计的核心是获得最大的分集增益、编码增益和吞吐量.在典型的无线通信系统中移动收发机从电池获得的功率是有限的，而且它的尺寸也应当比较小，为了延长电池的使用期限，只能采用低复杂度的编译码算法；而另一方面，基站对功率和物理尺寸方面的限制并不严格，我们可以在基站一端设置多个相互独立的天线.因此，在很多实际应用中，一个理想系统应该具有多个发射天线而且复杂度低，空时分组码（STBC）[3-4]正好满足这些要求，它不仅能够为系统提供满分集增益，而且编码和译码的复杂度非常低.

TCM能为系统提供编码增益[5]，而STBC只能为系统带来分集增益，级联码的初衷是以适当的系统复杂度为代价同时获取两种编码的优势[6-7].文中将搜索到的最小TCM好码应用于Alamouti提出的空分组编码中，并且与未使用TCM编码的系统作比较，验证TCM好码和级联码的性能.

1 TCM编码过程

在TCM系统中，为了不增加信号的带宽，需要扩张调制信号集以提供编码所需的冗余度，同时必须最大化信号点间的欧氏距离.符号集分割是网格编码调制（TCM）方案的核心，分割的基本原则是将信号星座图划分成为若干个子集（subset）使得信号点之间距离变大.星座中共有2n+1个信号点，为使发送信号间欧氏距离最大化，将2n+1个信号点分割为若干个子集，新子集中信号点间的欧氏距离随着分割次数的增加而变大，即Δ1＜Δ2＜Δ3＜….图1给出了8 PSK调制信号集的分割过程.

图1 8PSK符号集的集合分割

将图1中最上层8 PSK信号集合逐次按照一分为二的方式进行子集划分.假设星座图的半径为单位1，则中各相邻点间的欧氏距第一次子集分割为集合B后，任意两个最近的黑色信号点的间氏距离与QPSK相同.第二次子集划分成集合C后，两黑色点间的距离进一步扩大为Δ3=2，欧氏距离与BPSK相同.显然Δ1＜Δ2＜Δ3，每次子集分割都使得信号点的欧氏距离不断变大.

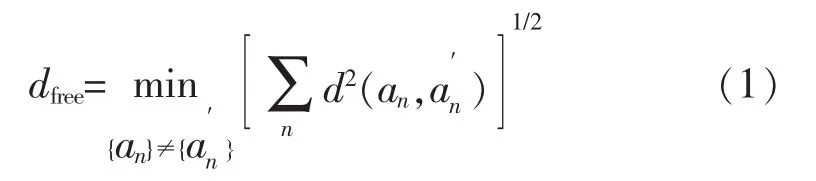
如果用此算法搜索TCM好码计算量很大，因此不得不对此算法进行简化.线性码的误差序列包含于信号集，定义误差序列为：

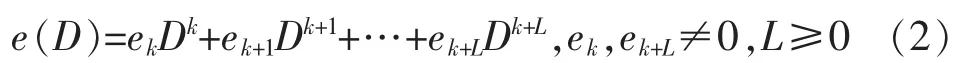
此外定义码字ei的欧氏重量：w（ek）=mind[a（z）,a（zei）]，其中z=「zm…z1，z0」，a（）表示码字到信号的映射，表示模2相加.则欧式自由距离等价于：

设q（ei）表示码字ei的尾零数，根据符号集分割规则可知码字ei的欧氏重量w（ei）≥q（ei），且在大多数情况下不等式取等号，则欧氏自由距离可以表示为：

满足上式的e（D）通常不止一个，因此取dfree=Δfree的风险比较小.采用上式搜索TCM好码时计算量显著减少，虽然使得欧氏距离精度下降，但是这个代价在允许的范围之内.在此基础上根据Larsen的自由距双向搜索算法[8]，同时采用若干舍去规则加快搜索速度[9].通过搜索可以得到具有最简编码器结构的好码，8 PSK系统最小TCM好码见表1.

表1 8PSK系统最小网格码好码

2 空时编码

Alamouti提出的空时分组编码[3]，为两发射天线系统提供完全的发射分集，随后Tarokh把Alamouti方案泛化到任意天线数目的发射天线环境中[4].STBC在接收端通过线性处理方式达到最大似然解码(ML).图2给出了Alamouti码的框图.

图2 Alamouti码的两天线发射分集机制

如图2所示，每1个符号周期都会有2个符号被分别从2副天线上发射.假设第1个符号周期中天线1上发射的信号为S1，天线2上发射的信号为S2.在下一个符号周期中，信号从天线1上发出去，天线2则发射信号.为考虑问题方便，先假设在连续的两个符号周期的时间内信道保持不变，有：

在t时刻从第一副和第二副发射天线到接收天线的衰落信道系数分别用h1和h2表θi（i=1，2）表示发射i到接收天线的幅度和相移.假定衰落系数在2个连续符号发射周期之间不变，在t时刻和t+T时刻接收端在2个连续符号周期内接收信号r1和r2可表示为：

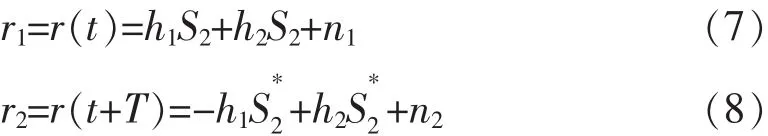
式中：n1，n2是均值为零、功率谱密度为N0/2的独立高斯变量，分别表示在t和t+T时刻AWGN的采样.

假设接收机完全地估计信道状态（信道衰落系数h1和h2已知），所有调制符的概率相等，最大似然译码准则（ML）是从所有调制符中选一对信使得下面的距离最小：

将上述两式代入上式，最大似然译码可以表示为：

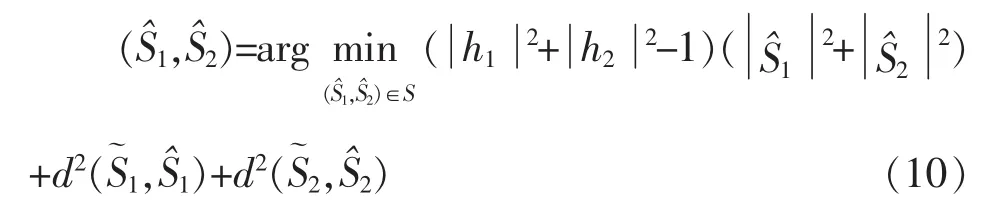
其中S是调制符所有可能的集合，d2（x，y）=是通过合并接收信号和信道状态产生的两个判决统计：

合并以上各式可以得到表达式：

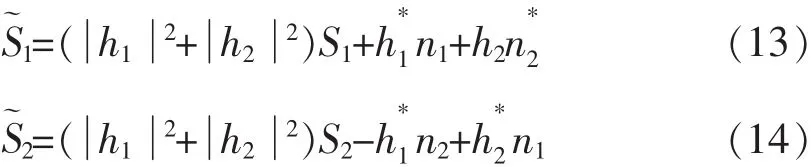
对于已知信道状态h1和h2，统计结1，2）是Si（i=1，2）的函数，可以将最大似然译码准则（ML）分解为两个独立的译码算法：

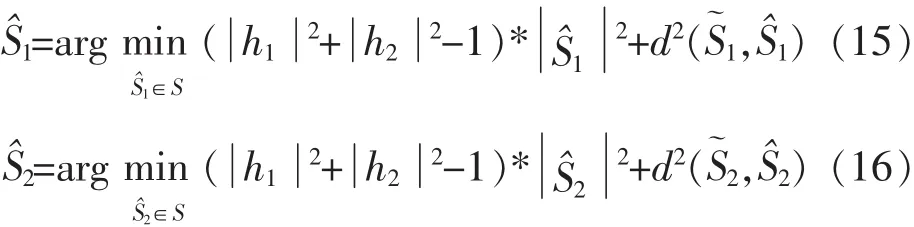
对于M-PSK星座，所有的调制信号的能量相等.因此译码准则可以写为

3 级联码方案

网格编码将编码和调制有机的结合在一起，可以为系统提供编码增益.空时分组码能够为系统提供满分集增益，而且编译码复杂度低.为了同时获得两种编码的优势将它们进行级联，图3为网格码和空时编码级联的结构图[10-11].

图3 编码STBC方案的编码器结构

如图3所示，在发送端信息比特流先经过TCM编码，然后将编码后的信息进行空时分组编码并进行发送；接收端先将接收到的信号进行合并，然后再将合并后的信息进行TCM译码并进行最终判决.TCM码选用搜索到的最简好码，码率为2/3，见表1.假定在某时刻输入4 bits信息经编码和8 PSK映射后得到两个符号S1和S2，然后对S1、S2进行STBC编码发送，经过信道后得到：

接收端对收到的信号进行合并得到：

信号合并方式与第2节相同，但是在译码的时候对得到的信号S˜1，S˜2不采用最大似然译码，而是直接送入TCM译码器，TCM解码器选择维特比译码[12].

4 性能仿真结果

为了验证上述方案的正确性和有效性，对其进行MATLAB仿真，比较STBC和TCM好码级联STBC方案两者之间的误码率.仿真采用Alamouti方案，两根发射天线和一根接收天线；每个信噪比下发送2000 bits信息统计其误码率；信道满足Rayleigh分布，两种方案经历的信道相同.STBC的调制方式选择QPSK，级联码采用8 PSK调制.相同带宽下，两者的频率利用率都为2 bit/s/Hz，且每根天线发送的符号功率都相同.仿真结果如图4所示.

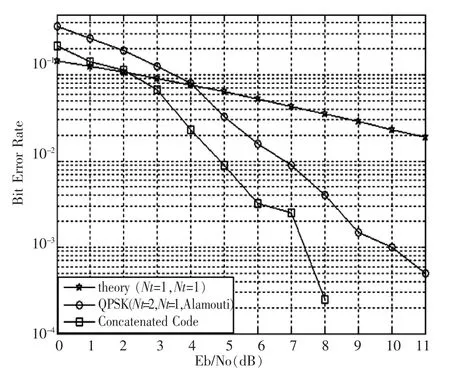
图4 STBC和级联码的性能比较

如图4所示，把QPSK调制下的STBC误码率曲线与传统的单发单收系统的理论误码率作比较，可以发现虽然STBC没有编码增益但是它可以为系统提供了很好的分集增益.再观察STBC+TCM方案的误码率曲线，它不仅和STBC一样拥有很好的分集增益，而且性能也比STBC方案更好.误码率为时，STBC+TCM方案比STBC有2.6 dB的性能提高.

5 结束语

TCM调制方式的性能比传统的调制方式有很大的提高，其设计核心是增大信号点间的欧氏距离，但是如果直接用欧拉公式搜索TCM好码计算量将非常大，为此不得不对该公式进行简化并且增加一些规则加快搜索速度.文中将搜索到的TCM好码应用于空时编码，TCM好码能够给系统带来编码增益，将TCM与Alamouti分组码级联并且与QPSK调制下Alamouti码的性能进行比较，虽然级联码增加了系统的复杂度，但是它在不提高天线发射功率或损失频带利用率条件下取得了更好的系统性能.

[1]Ungerboeck G.Channel coding with multilevel/phase signals[J].IEEE Transactions on Information Theory，1982，28(1)：55-67.

[2]严家明，张艳峰，仵敏娟.网格编码调制在无线信道下的应用[J].计算机仿真，2007，24(12)：134-137.

[3]Alamouti S M.A simple transmit diversity technique for wireless communications[J].IEEEJournalonSelectedAreasinCommunications，1998，16(8)：1451-1458.

[4]Tarokh V，Jafarkhani H，Calderbank A R.Space-time block codes from orthogonal designs[J].IEEE Transactions on Information Theory，1999，45(5)：1456-1467.

[5]胡炳轻.TCM网格编码调制技术编码增益分析[J].无线电工程，2008，38(16)：14-15.

[6]Yi Gong，Ben Letaiefn K.Concatenated space-time block coding withtrelliscodedmodulation in fading channels[J].IEEE Transactions on Wireless Communications,2002，1(4)：580-590.

[7]伍建辉，王毅.无线通信系统级联码的选择与实现[J].火控雷达技术，2011，40(3)：96-100.

[8]Larsen.Comments on“An efficient algorithm for computing free distance”[J].IEEE Transactions on Information Theory，1973，19(4)：577-579.

[9]曹志刚，居红兵.TCM好码的计算机搜索[J].电子学报，1991，19（6）：65-72.

[10]敖珺，马春波，敖发良，等.交织的空时分组码级联不对称网格编码调制方法[J].通信学报，2010，31(1)：100-104.

[11]居美艳，酆广增.网格编码调制与空时块码的级联和空时格码的比较[J].南京邮电学院学报，2004，24(4)：46-50.

[12]吴军，钟东波.OFDM基带系统接收器中高性能Viterbi译码器的FPGA实现[J].江西理工大学学报，2011，32(3)：60-64.

Space-time coding with powerful TCM code

WU Jun,SUN Tao,ZHONG Yan-wan,WU Xiao-bo

(School of Information Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China)

Trellis coded modulation(TCM)considers modulator and encoder as a whole and makes the Euclidian free distance between signal sequences maximum.It can achieve better performance without expanding the bandwidth or improving the power.This paper describes simplified algorithm to search for powerful TCM codes at first.Then the TCM code is applied to space-time code.Finally it compares performances of space-time block coding(STBC)with the concatenated STBC with minimal powerful TCM code in terms of bit error rate(BER)under the condition of same symbol transmit power,data rate and bandwidth efficiency.It verifies the wonderful performance of minimal powerful TCM code and the concatenated code.

Trellis coded modulation;Space-time block coding;concatenated coding

TN911.22

A

2012-03-28

江西省教育厅科技计划项目（GJJ12354）

吴军（1963-），男，副教授，主要从事空时编码和数字信号处理等方面的研究，E-mail：wswujun@126.com.

2095-3046（2012）03-0062-04