基于离散伴随方法的透平叶栅压力反设计研究

张朝磊，吴海燕

（1.江西理工大学机电工程学院，江西赣州341000；2.西安交通大学叶轮机械研究所，西安710049）

基于离散伴随方法的透平叶栅压力反设计研究

张朝磊1,2，吴海燕1

（1.江西理工大学机电工程学院，江西赣州341000；2.西安交通大学叶轮机械研究所，西安710049）

根据离散伴随方法理论和自动微分技术，由流场求解器源代码构造了相应的离散伴随场求解器.通过耦合参数化程序、网格生成程序、流场求解器和伴随场求解器，建立了适用于叶轮机械叶栅的气动优化设计系统.利用该系统，对某二维跨音速透平叶栅在给定叶型表面目标压力分布的情况下，通过构造合适的目标函数将叶栅反设计问题转化为叶栅气动优化设计问题，成功进行了气动反设计.反设计结果表明，文中建立的叶栅气动优化设计系统能够根据给定的叶型表面压力分布有效地进行压力反设计，验证了该方法的正确性与有效性.

离散伴随方法；自动微分；透平叶栅；反设计；灵敏度

0 前言

基于控制理论的伴随方法能够实现快速精确的敏感度分析，并且敏感度计算量与设计变量数无关，有效克服了传统敏感度分析方法计算量正比于设计变量数的问题[1].基于伴随系统建立方式的不同，伴随方法可以分为连续伴随方法和离散伴随方法.与连续伴随方法相比，离散伴随方法具有目标函数适用性广，伴随系统建立过程清晰、规范，存在成熟的自动微分工具用于辅助开发与考核伴随系统等优势.自上世纪九十年代以来该方法得到了相关研究者的关注[2-5].目前，离散伴随方法在外流领域取得了一定的研究成果，在机翼乃至整机的气动优化设计中得到了广泛应用.在内流领域，离散伴随方法自本世纪初以来逐步得到关注与发展，目前，研究人员已经成功将其应用于叶轮机械叶栅的气动优化设计与反设计[6-11].

基于文献[10-11]中的离散伴随求解器实现方法，编程实现了无粘环境下的离散伴随场求解器；建立了适用于透平叶栅气动反设计的设计系统，并利用该系统对某二维跨音速透平叶栅在给定叶型表面目标压力分布的情况下，通过构造适当的目标函数对该叶栅进行了气动反设计.

1 离散伴随系统原理

通过构造适当的目标函数，可以将叶轮机械叶栅的气动反设计问题转化为优化设计问题.通常，叶轮机械叶栅优化设计对应的最小值问题可表示为：

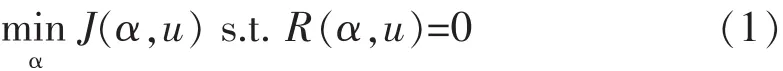
其中，目标函数J为设计变量α和状态变量u的函数，同时，状态变量u本身受状态方程（Euler方程）R（α，u）=0约束.引入伴随变量υ，定义新的目标函数I：

线性化上述目标函数，令目标函数对状态变量的变分系数为零，消除目标函数对状态变量敏感度的依赖，并引入时间相关项，可得到离散伴随系统方程如下：

伴随方程（3）中不存在对设计变量α的导数，因此伴随方程的求解独立于设计变量α的个数.在求得伴随变量υ后，目标函数的梯度可按下式计算：

由公式（3）和（4）可知，为了求解目标函数对设计变量的梯度，关键在于计算J/u、J/α、υT（R/α）以及υT（R/u），其中前三项的计算不需要迭代计算，而最后一项的求解必须迭代求解.

2 自动微分

自动微分是一种由某计算程序自动生成对应导数计算程序的技术，其理论依据为微积分的链导法则和程序各步操作可微性的假设.自动微分工具的实现方式主要包括两种，即基于源代码转换实现和基于运算操作符重载实现.通常，基于运算符重载的自动微分工具需要计算机语言支持运算符重载，自动微分过程不重新生成代码，一般情况下其导数程序计算效率较低；基于源代码转换的自动微分工具通常必须根据原有计算程序另外生成导数计算程序，并且生成的自动微分程序计算效率也比较高.

自动微分可分为两种模式，即前向模式和后向模式.通过自动微分，对于一个标量函数f和某一向量，前向模式给出了其方向导数Δf·，而其后向模式给出了其梯度Δf；而对于一个向量函数R和某一向量，前向模式给出了ΔR·，而后向模式给出了（ΔR）T·.因此，采用后向模式对计算流体力学源代码中残差子程序进行自动微分处理，即可获得公式（3）和（4）中所需要的各项.本研究中采用的自动微分工具为Tapenade[12]，该工具基于源代码转换实现.

3 离散伴随系统求解

3.1 灵敏度传递

在叶轮机械的数值计算中，从对应于某几何模型的一组设计变量α到某一确定的计算网格X，再到流场数值解U和目标函数J，其间关系可表述如下：

3.2 伴随场迭代求解

伴随场的迭代求解策略与文献[10,11]中相似，本研究中伴随变量的迭代求解公式可写为：

为了获得目标函数对设计变量的导数，在求得伴随场之后，利用公式（8）间接实现目标函数对设计变量梯度的计算.即：

4 优化流程

与文献[10]中建立的叶轮机械叶栅气动优化设计系统相似，文中建立的叶轮机械叶栅反设计系统包括参数化、网格生成、流场计算、伴随场计算、梯度计算及优化子程序六部分.其中叶栅参数化基于非均匀B-Spline实现；网格生成基于边界规范化方法和Laplace网格光顺技术实现；梯度计算过程中计算网格对设计变量的梯度基于中心差分方法实现，优化子程序基于拟牛顿法实现.整个叶栅反设计系统流程如图1所示.

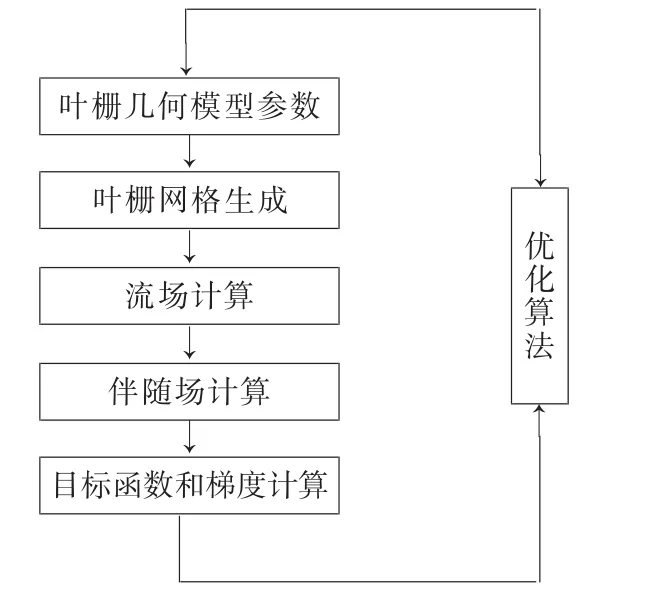
图1 反设计系统组成及流程

5 反设计算例

基于建立的叶栅反设计系统，针对某跨音速叶栅在粘性环境下进行了气动反设计.该叶栅的气动参数如表1所示.

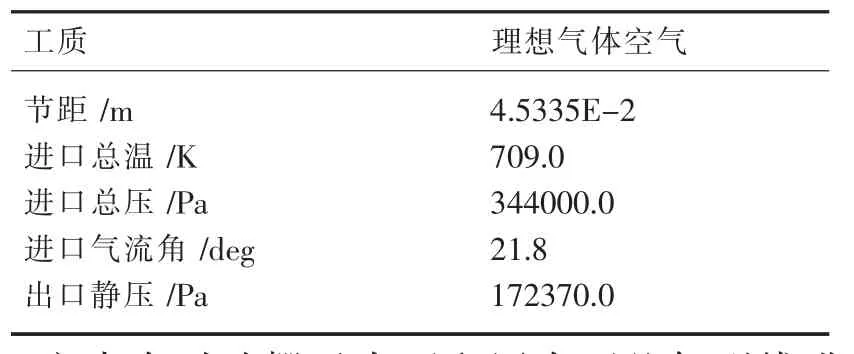
表1 叶栅气动参数

文中在对叶栅吸力面和压力面几何型线进行参数化之前，首先根据设定的前缘和尾缘比例因子进行叶栅前缘、尾缘和中间区域的分割，然后对吸力面和压力面的中部区域进行参数化.鉴于叶栅的优化或反设计过程中叶栅前缘和尾缘的几何型线通常是保持不变的.因此，采用文中的参数化方法，即仅针对中部区域进行参数化不仅可以保证叶栅的前缘和尾缘形状，减少参数化所需要的控制点数目，而且可以有效消除叶栅尾缘附近区域叶栅几何型线的波动.文中的叶栅参数化基于上述方法，首先设定叶栅吸力面前缘和尾缘占吸力面型线长度的5%为固定不变区域，其余部分为中部区域.分割后中部区域叶栅型线采用10个控制点进行参数化，参数化的结果如图2所示.在反设计过程中，控制点3rd-8th的坐标选为设计变量，变量总数为12.

叶栅网格生成采用H-O-H型网格拓扑结构，各块网格生成采用边界规范化方法，然后采用Laplace方法进行光顺，计算网格节点数均为9467.计算网格示意图如图3所示.

流场和伴随场计算过程中边界条件给定如下：进口给定总压、总温和进口气流方向；出口给定平均静压；叶片表面给定绝热无滑移壁面边界条件.计算区域为单通道，叶栅两侧面网格给定位移型周期性边界条件.

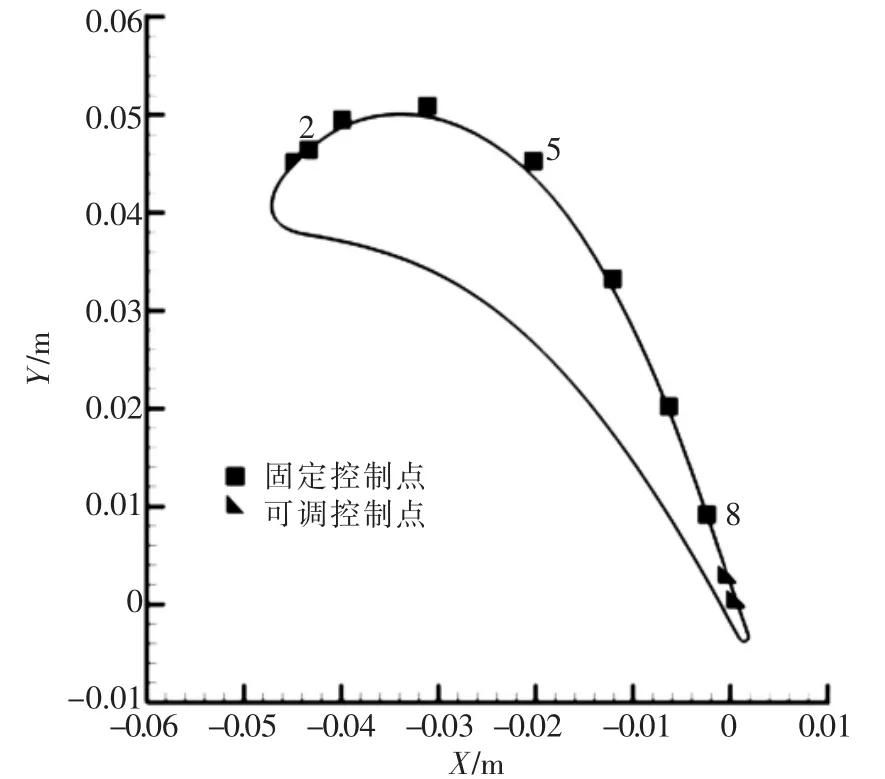
图2 叶栅参数化结果

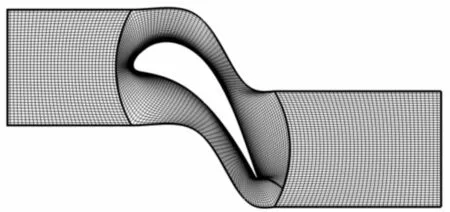
图3 计算网格

反设计过程中，通过给定叶栅表面目标压力分布，构造目标函数如下：

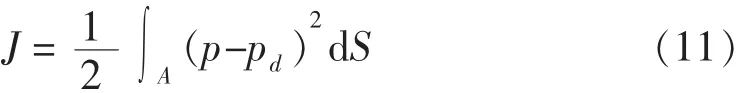
其中pd为目标压力分布.优化设计采用拟牛顿算法，反设计过程中目标函数收敛史如图4所示，图中目标函数值以初始值为参考进行了归一化处理，经过11次迭代后收敛，期间共计算了12次伴随场，24次流场.优化前后目标函数对设计变量的梯度对比如图5所示，从图可见，反设计结束时目标函数对设计变量的梯度趋近于零.

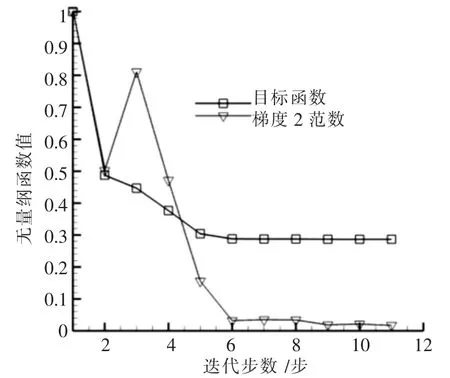
图4 目标函数收敛史

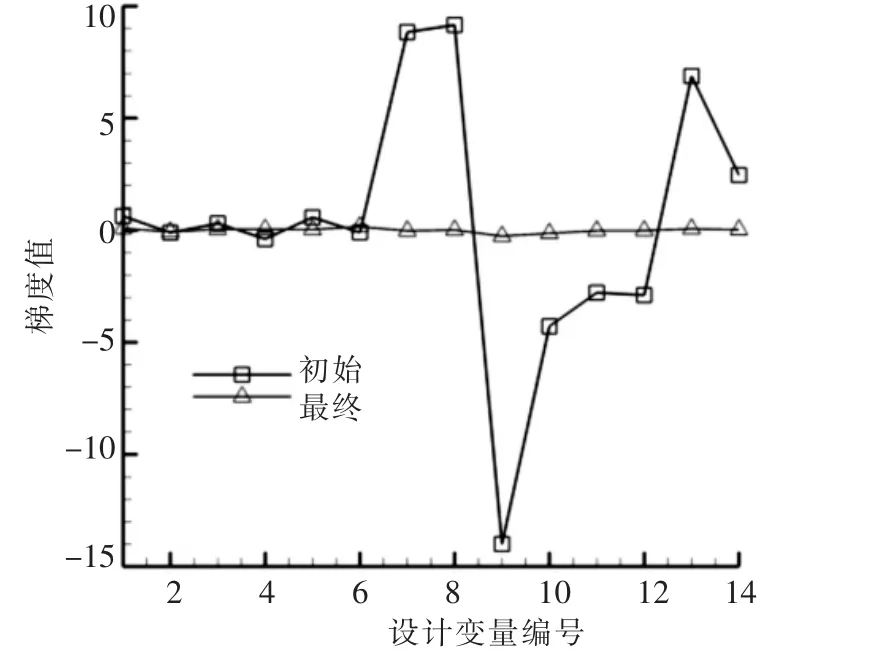
图5 设计前、后设计变量灵敏度对比

反设计前、后叶栅表面压力对比如图6所示.反设计前后叶栅型线对比如图7所示.从图可见，反设计后，叶栅表面压力与给定的目标压力分布基本重合，验证了文中建立的叶轮机械叶栅反设计系统的正确性与有效性.

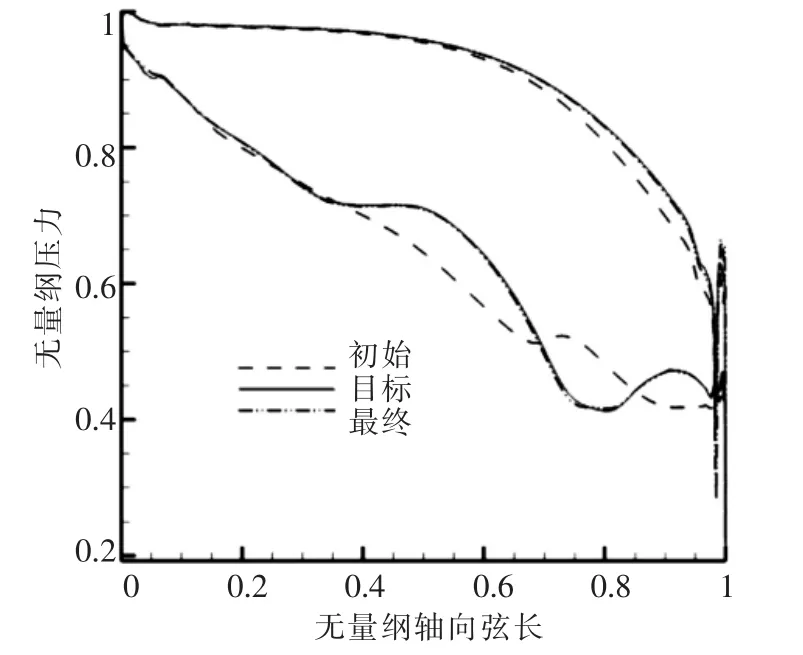
图6 反设计前、后叶片壁面压力对比

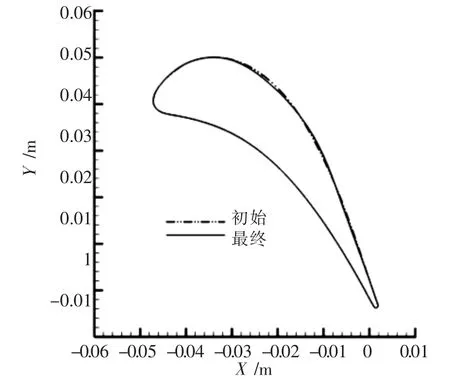
图7 反设计前、后叶型对比

6 结论

文中建立了基于离散伴随方法的叶轮机械叶栅气动优化设计系统，并利用该系统在无粘环境下根据指定的目标压力分布对一跨音速叶栅进行了压力反设计，反设计结果验证了文中建立的叶栅气动优化设计系统的正确性与有效性.文中提出的叶栅参数化方法和开发的离散伴随场求解器可直接应用于三维叶轮机械叶栅的气动反设计，为下一步叶栅三维反设计优化奠定了基础.

[1]刘静，丁凌蓉.基于Matlab的低矮式破碎机V带传动模糊优化设计[J].江西理工大学学报，2009，30(2)：24-27.

[2]Elliott J，Peraire J.Practical 3D aerodynamic design and optimization using unstructured meshes[J].AIAA Journal，1997，35(9)：1479-1485.

[3]Mohammadi B.Optimal shape design，reverse mode of automatic differentiation and turbulence[C].AIAA Paper，1997，97-99.

[4]Giles M B，Pierce N A.Adjoint equations in CFD：duality，boundary conditions and solution behavior[C].AIAA Paper，1997，97-1850.

[5]Marta A C，Mader C A，Martins J R R A，et al.A methodology for the developmentofdiscreteadjointsolversusingautomaticdifferentiation tools[J].InternationalJournalofComputationalFluidDynamics，2007，21(9-10)：307-327.

[6]FloreaR，HallKC.Sensitivityanalysisofunsteadyinviscidflowthrough turbomachinery cascades[J].AIAA Journal，2001，39(6)：1047-1056.

[7]Campobasso M S，Duta M C，Giles M B.Adjoint methods for turbomachinery design[C].ISABE Conference，2001.

[8]DutaMC，GilesMB，CampobassoM S.The harmonic adjoint approach to unsteady turbomachinery design[J].International Journal for Numerical MethodsinFluids，2002，3(3-4)：323-332.

[9]Campobasso M S，Duta M C，Giles M B.Adjoint calculation of sensitivities of turbomachinery objective functions[J].AIAA Journal of Propulsion and Power，2003，19(4)：693-703.

[10]张朝磊，厉海涛，丰镇平.基于离散伴随方法的透平叶栅气动优化设计[J].工程热物理学报，2012，33(1)：47-50.

[11]Zhang C L，Feng Z P.Aerodynamic shape design optimization for turbomachinery cascade based on discrete adjoint method[C].ASME Paper GT2011-45805.

[12]Hascoёt L，Pascual V.Tapenade 2.1 user’s guide.Technical Report 0300[R]，INRIA，2004.

Study on pressure inverse design of turbomachinery cascade based on discrete adjoint method

ZHANG Chao-lei1,2,WU Hai-yan1
(1.School of Mechanical and Electrical Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China;2.Institute of Turbomachinery,Xi'an Jiaotong University,Xi'an 710049,China)

A discrete adjoint solver is constructed according to the discrete adjoint theory and the automatic differentiation technology based on an in-house flow solver code.An aerodynamic optimization design system for turbomachinery cascades is established by coupling a parameterization program,a structured multi-block grid generator,a flow solver and the discrete adjoint solver established in this work.Based on the optimization system,the pressure inverse design problem could be translated to an optimization problem by constructing the objective function appropriately.An inverse design for a typical 2D transonic turbomachinery cascade is preformed under the inviscid flow environment according to the target pressure distribution specified beforehand.The inverse design result indicates that the optimization system established in this article could implement the pressure inverse design efficiently.The validity and efficiency of the optimization design system are proved.

discrete adjoint method;automatic differentiation;turbomachinery cascade;inverse design;sensitivity

V228.7

A

2012-02-13

国家自然科学基金资助项目（51076121）；江西理工大学科研基金项目计划（JXXJ11038）

张朝磊（1979-），男，在读博士，讲师，主要从事叶轮机械气动优化设计等方面的研究，E-mail：zhangchaolei@yahoo.cn.

2095-3046（2012）03-0047-04