基于可行域法的斜拉桥索力优化
2012-01-10郭钟群谢志华赵奎谢良林旭
郭钟群,谢志华,赵奎,谢良,林旭
(1.江西理工大学,a.建筑与测绘工程学院;b.工程研究院,江西赣州341000;2.上海大学土木工程系,上海200072)
基于可行域法的斜拉桥索力优化
郭钟群1a,谢志华1a,赵奎1b,谢良1b,林旭2
(1.江西理工大学,a.建筑与测绘工程学院;b.工程研究院,江西赣州341000;2.上海大学土木工程系,上海200072)
斜拉桥在合理成桥状态下的索力优化计算,是斜拉桥结构设计分析中的重要步骤.文中阐述了运用可行域法的索力优化算法,并运用MATLAB程序计算结果来实现对斜拉桥的索力优化计算.结合某斜拉桥索力优化的算例,把可行域算法结果与通用的优化计算结果进行比较,两者结果非常接近,表明可行域算法应用于斜拉桥的索力的优化结果有效,具有较好的实用价值.
斜拉桥;可行域法;索力;优化
0 引言
随着设计理论的不断完善、施工方法的改进和新型建筑材料的利用,斜拉桥建设正进入一个快速发展的时代[1].斜拉桥在合理成桥状态下索力的优化计算,是斜拉桥结构设计分析中的重要步骤.斜拉桥的结构体系确定以后,其成桥受力状态主要由斜拉索的索力决定.通过调整索力来改善结构的受力状态,可以使斜拉桥结构的受力更加合理[2].采用优化计算方法,总能找到一组索力,在固定荷载作用下,使反映某种受力性能的结构体系指标达到最优,在活载作用下主梁受力安全,这组索力所对应的成桥状态就是所谓的合理成桥状态[3].因此,斜拉桥成桥状态的优化计算也就转化为斜拉桥索力的优化计算问题,索力优化调整问题是大跨度斜拉桥结构优化设计的重要组成部分[4-6].文中阐述了基于可行域法的索力优化算法,结合某算例运用MATLAB程序来实现对斜拉桥的索力优化计算,并与通用的优化算法进行比较,探讨基于可行域法的斜拉桥索力优化计算结果的合理性与有效性.
1 斜拉桥索力优化方法
1.1 斜拉桥索力优化的概念
索力优化即在斜拉桥的结构体系被确定之后,寻找一组斜拉索力,使结构在确定荷载作用下,某种反映受力性能的目标达到最优[7-8].
在斜拉桥计算的索梁组成的一次超静定体系中(如图1所示),赘余力用拉索的张力N表示,梁的弯矩为:

若按变形协调条件计算赘余力,可得:
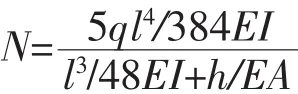
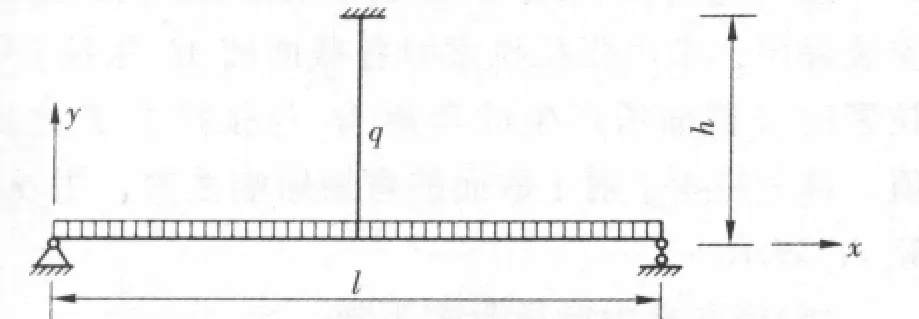
图1 斜拉桥计算的索梁组合一次超静定体系
对应的弯矩图如图2(b)所示,这一状态相当于优化后的斜拉桥恒载状态.这时的内力状态是通过索的张拉来实现的.相应的索力不能使结构满足变形协调,正是这一张拉力,改善了梁的受力状况[9].
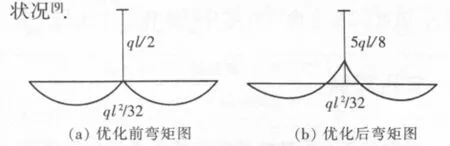
图2 斜拉桥计算的索梁组合处优化前后弯矩图
在斜拉桥的设计当中,对于合理成桥状态(如梁、塔中弯曲应变能最小)的确定通常可以先不考虑施工过程,只根据成桥状态的受力图来计算,然后按施工过程将索的张拉程序逐个细化[10-11].于是便出现了关于索力调整和索力的优化问题.斜拉桥的成桥状态索力优化问题可以分为两大类:无约束索力优化法和有约束索力优化法.
1.2 无约束索力优化法
无约束优化法的做法是设定某一目标,寻求一组索力来满足已设定的目标,这种方法仅关心反映受力性能的目标达到最优,而不关心索力的大小和分布.主要包括以下几种方法:①简支梁法;②刚性支承连续梁法;③零位移法;④内力(或应力)平衡法;⑤以结构的弯曲能量最小作为优化目标的弯曲能量最小法;⑥以结构弯矩平方和最小作为优化目标的弯矩最小法[12].
1.3 有约束索力优化法
有约束索力优化法是指在确定了总体优化目标的同时,又关心某些指定截面构件的内力、位移的优化方法.主要包括以下几种方法:①限定索力法;②用索量最小法;③最大偏差最小法;④可行域法.
2 基于可行域法的斜拉桥索力优化
可行域法从控制主梁应力的角度出发,索力过大或过小都有可能造成主梁上、下缘拉应力或压应力超限,因而期间必定存在一个索力可行域,使主梁在各种工况下各截面应力均在容许范围之内[13-14].
2.1 恒载平衡法索力初拟
对于主跨进行索力初拟计算(如图3所示),忽略主梁抗弯刚度的影响,则Gm为第i号索所支承的恒载质量,根据竖向力的平衡,得到:

拉索引起的水平力:

进一步考察边跨,忽略塔的抗弯刚度,则主、边跨拉索的水平分力应相等,得到:
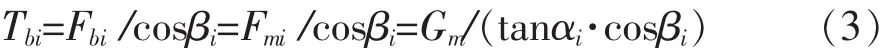
边跨第i号索支承的恒载质量Gb可依据Tbi作相应的调整:
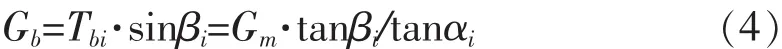

图3 索力初拟计算图
2.2 可行域法调索技术
主梁截面的应力控制条件按以下的公式表示.
2.2.1 拉应力控制条件
主梁截面上、下缘在恒载和活载共同作用下的上下缘最大拉应力应满足:
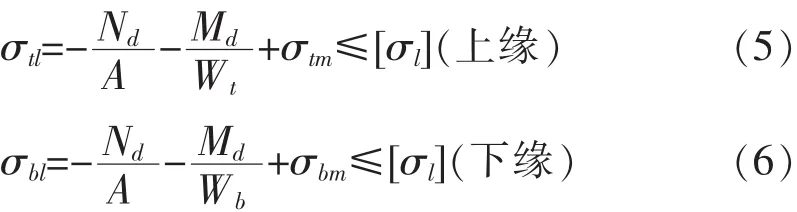
2.2.2 压应力控制条件
主梁截面上、下缘在恒载和活载组合作用下的上下缘最大压应力应满足:

式中:Nd、Md—全部恒载(包括预应力)产生的主梁截面轴力和弯矩,轴力以压为正,弯矩以下缘受拉为正;A、Wt、Wb—主梁的面积、上缘和下缘抗弯抵抗矩;σtm、σbm—其他荷载(除恒载)引起的主梁截面上、下缘最大应力(应力以拉为正,压为负,下同);σtn、σbn—其他荷载(除恒载)引起的主梁截面上、下缘最小应力.
2.2.3 主梁恒载弯矩的可行域
在以上应力控制条件的关系式中,Md是通过调索预期达到的恒载弯矩,系待求值,由式(5)~(8)可得:

在式(9)中,令:
Md1=min(Mdl2,Mda1)(控制恒载正弯矩)
Md2=max(Mdl1,Mda2)(控制恒载负弯矩)
则主梁恒载弯矩的可行域(如图4所示)为:

在主梁上施加预应力可增大可行域的范围,调索的最终结果不仅应使主梁恒载弯矩全部进入可行域,而且索力分布应较均匀.

2.2.4 恒载弯矩计算的影响矩阵法
为了达到通过调索,使主梁各截面的恒载弯矩进入上述可行域内的目标,可按下述影响矩阵法计算各拉索的初张力:
(3)按上述应力控制条件,计算各控制截面的恒载弯矩可行域{Md}.
(4)将各控制截面当前恒载弯矩{M′d}与{Md}中值的差值作为索力调整的弯矩增量目标:

(5)计算斜拉索恒载弯矩影响系数.模拟主梁安装程序,求出张拉拉索时各截面的M.张拉j号拉索时,i截面所产生的弯矩Mij与张拉力Ti之比值,称为拉索j对i截面的弯矩影响系数,用αij=Mij/Ti表示.
(6)建立索力增量影响矩阵:

控制截面的位置,对于密索体系的斜拉桥宜选在拉索锚固截面,对于稀索体系的斜拉桥则宜选在两锚固点间的跨中.
(7)将求得的初始索力{T},重新代回第(2)步继续计算,直到所有控制截面的恒载弯矩全部落入可行域内为止.
需要指出的是,对于拉索一次张拉的情形,合拢段的内力与初始索力大小无关,若合拢段的内力过大,就必须在合拢后对部分拉索作二次张拉.
3 应用算例
根据基于可行域法的斜拉桥索力优化的理论,再利用连续梁内力计算和连续梁的影响线计算方法,对基于可行域法的斜拉桥索力优化方法编制MATLAB程序,实现程序化.为验证其可行性,采用一个算例,并针对算例所给出的原解答进行对比分析.
如图5所示是一座对称型独塔斜拉桥的右侧桥跨(图中单位为m),该跨内共有三对拉索.已知每对拉索的总面积A=0.015m2,二期恒载q恒=46kN/m,混凝土强度等级C50,重度γ=26 kN/m,位于拉索下锚处的横隔板厚t隔=30 cm,V主梁纵向施加了F=3000 kN的预应力(轴心受压),汽车荷载在3个控制截面产生的应力如表1所示.计算索力Ti和控制截面恒载弯矩Md.
传统优化算法的计算结果如表2所示,基于可行域法的MATLAB程序运行结果如表3和表4所示.
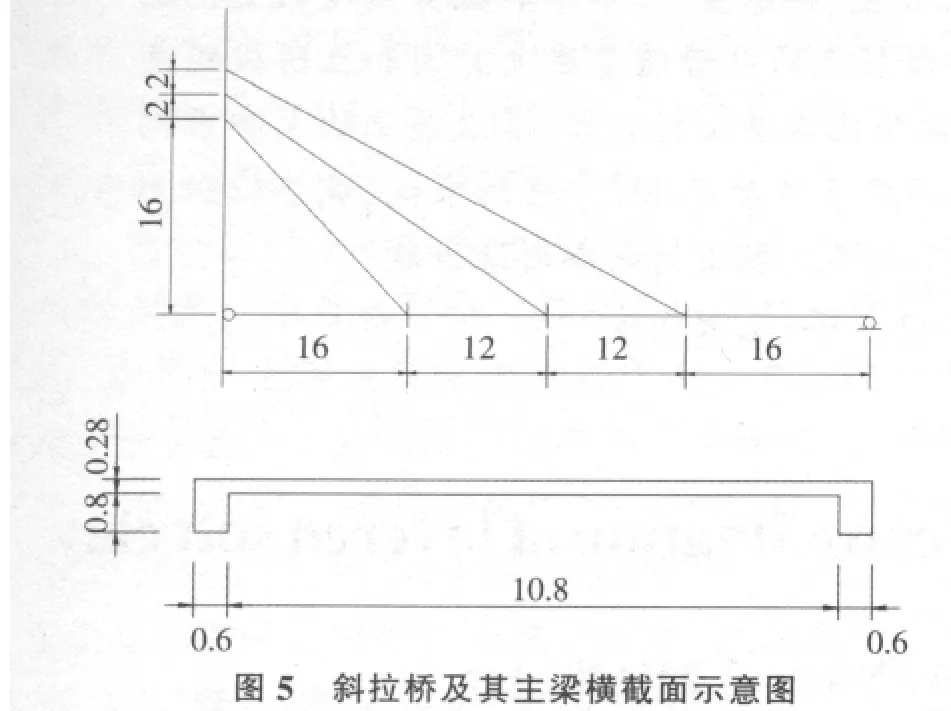
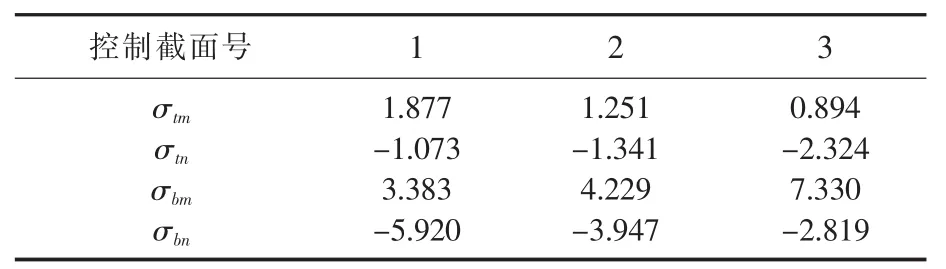
表1 控制截面汽车荷载应力/MPa
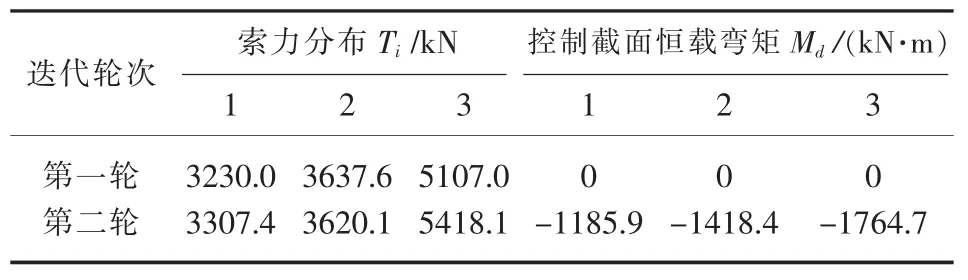
表2 迭代计算汇总表
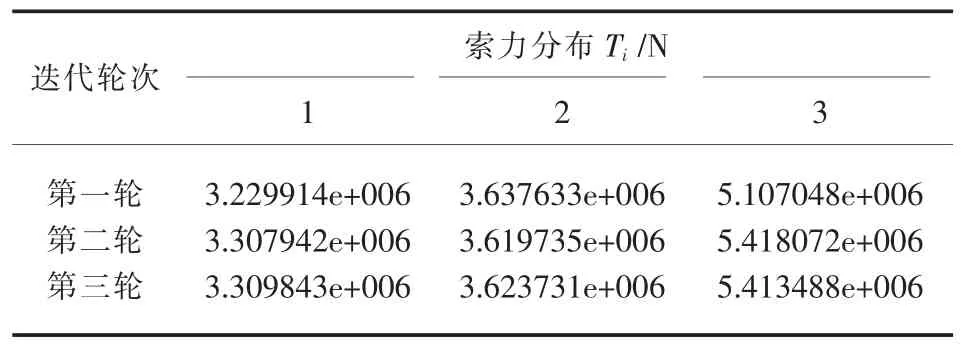
表3 可行域法计算结果(索力)汇总表
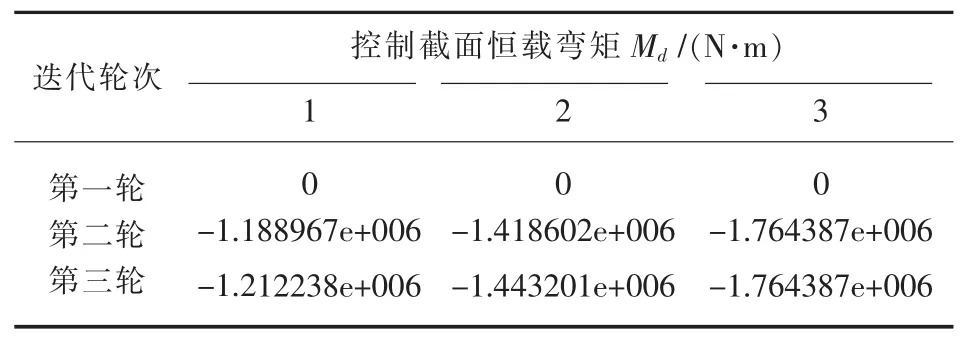
表4 可行域法计算结果(控制截面弯矩)汇总表
结果分析:通过算例给出索力优化的解答结果与程序计算所得到的结果,可以看出程序进行了三轮次的计算,前两轮的计算结果均与原题所给解答非常接近,误差已经达到了所限制的范围之内,故认为基于可行域的斜拉桥索力优化分析程序是正确的、可行的.同时,将程序计算所得到的第二轮索力与第三轮索力相比较,索力更趋向于平均,变化幅度已经十分小,没有再重复迭代计算的价值,所以程序从第三轮计算之后终止运行.
4 结论
(1)利用可行域法对斜拉桥结构设计中的索力进行优化调整,跟通用的优化计算结果基本一致,说明基于可行域法的斜拉桥索力优化方法结果有效,是一种可行的方法.
(2)随着信息技术日趋成熟,借助计算机语言对优化算法进行编程计算,使得斜拉桥的结构分析计算必然更加便捷化、合理化以及精确化.
(3)完善基于可行域法的斜拉桥索力优化程序,增强其通用性,将许多因简化而未考虑的因素纳入到程序中来,使程序计算更接近于真实情况,使其能够解决不同情况下的实际问题.
[1]梁鹏,肖汝诚,张雪松.斜拉桥索力优化实用方法[J].同济大学学报,2003,31(11):1270-1274.
[2]刘士林.斜拉桥[M].北京:人民交通出版社,2002.
[3]郑一峰,黄侨,孙永明.部分斜拉桥合理成桥状态的研究[J].公路交通科技,2006,23(11):60-63.
[4]刘志勇.斜拉桥斜拉索索力测试方法综述[J].铁道建筑,2007(4):18-20.
[5]马林,魏峰.北京市五环路斜拉桥的索力测试和分析[J].铁道建筑,2008(1):13-15.
[6]黄海云,张俊平,刘爱荣,等.自锚式悬索桥吊索张拉过程中索力变化规律的试验研究[J].铁道建筑,2010(4):10-13.
[7]江文武,李国建.基于数值模拟与静载试验的新华桥质量检测分析[J].江西理工大学学报,2011,32(5):9-12.
[8]高建勋.斜拉桥索力测试方法及误差研究[J].公路与汽运,2004(4):80-81.
[9]孙昊,钱永久,窦勇芝.基于信赖域优化算法的斜拉桥索力优化设计[J].公路交通科技,2008,25(11):78-81.
[10]李岩,陈彦江,盛洪飞,等.基于Matlab优化工具箱的斜拉桥索力优化实用方法[J].森林工程,2006,22(6):35-37.
[11]徐靖.浅析斜拉桥合理成桥索力确定的方法[J].中国水运:理论版,2006,4(8):67-68.
[12]李的平,戴公连.三索面斜拉桥成桥索力优化分析[J].中外公路,2008,28(3):94-99.
[13]雷丽恒.斜拉桥索力优化设计探索[J].中外公路,2006,26(6):77-80.
[14]侯亚君,高峰.可行域为有限集的多目标规划的一种解法[J].沈阳航空工业学院学报,1997,14(3):65-68.
The cable tension optimization based on the feasible domain method
GUO Zhong-qun1a,XIE Zhi-hua1a,ZHAO Kui1b,XIE Liang1b,LIN Xu2
(1 Jiangxi University of Science and Technology,a.Faculty of Architectural and Mapping Engineering;b.Engineering Research Institute,Ganzhou 341000,China;2.Department of Civil Engineering,Shanghai University,Shanghai 200072,China)
The calculation of cable tension optimization for the cable stayed bridge in a reasonable state is an important step in the structure design and analysis of cable stayed bridge.This paper describes the application of feasibledomainmethodincableforce optimization algorithm,and uses the results of MATLAB software programming to achieve the cable force optimization.Referring to a cable stayed bridge′s cable force optimization example,and comparing the feasible domain algorithm results with a general optimization calculation results,the calculation results of the two methods are very close.The results show that the feasible domain algorithm applied to the cable force optimization results is effective and practical.
Cable stayed bridge;the feasible domain method;cable tension;optimization
U448.27
A
2012-04-20
国家自然科学基金资助项目(50464002);江西省教育厅青年科学基金资助项目(GJJ09518)
郭钟群(1987-),男,硕士研究生,主要从事结构工程等方面的研究,E-mail:guozhongqun_jxust@163.com.
赵奎(1969-),男,博士,教授,主要从事岩石力学测试与工程稳定性分析等方面的研究,E-mail:yglmf_zk@163.com.
2095-3046(2012)03-0010-04
