由EUROBRIDGE'97地震剖面的P波与S波速度模型和重力数据得到的岩石层上部密度—速度关系

E.Kozlovskaya T.Janik J.Yliniemi G.Karatayev M.Grad

由EUROBRIDGE'97地震剖面的P波与S波速度模型和重力数据得到的岩石层上部密度—速度关系

E.Kozlovskaya T.Janik J.Yliniemi G.Karatayev M.Grad

传统的折射与广角反射地震和重力数据的联合解译是基于大量地壳岩石弹性性质实验室研究证实的地震P波速度和密度之间众所周知的相关性。与这一方法相矛盾的一个问题是富含钙长石的岩石具较高的P波速度，而不满足常规密度—VP关系。这说明基于常规密度—VP关系的联合反演不适用于横跨大的非造山带环斑－辉长－斜长岩地块的广角地震调查，因为其组成成分富含斜长石。同时使用VP和VS计算密度模型就可解决这一问题。岩石属性的实验室结果表明密度与VS相关性很强。此外，各向同性VS与密度的相关性较VP更强，且受高斜长石含量的影响更小。即便如此，利用这一已知的密度与VS或者密度与VP及VS的相关性进行地震和重力数据的联合反演仍然十分少见。其重要原因在于暴破地震学中S波波至的质量低，因而难以得到可靠的S波速度模型。

本文阐述了在乌克兰地盾EUROBRIDGE'97广角反射和折射剖面所做的地震和重力数据联合反演的结果。该区缺失厚沉积体，使我们可以得到P波和S波速度模型。通过重力反演得到EUROBRIDGE'97剖面密度模型，我们利用密度和VP、VS模型的关系，将密度模型参数化。这样参数化后，经重力数据转换，可以获得密度和地震波速的关系。结果显示EUROBRIDGE'97剖面的密度与地震波速之间呈非线性和离散的关系。对相关性的分析表明，造成离散是缘于横跨该剖面的大的地质构造单元的差异。为解释这一差异，我们对比EUROBRIDGE'97剖面上3个主要地质单元中地震速度和密度的关系和来自乌克兰地盾及另一个前寒武纪地区的岩石学资料。可见与平均密度—速度关系的偏移量是岩石的特殊矿物组合的反映，包含了不同的岩石时代和地壳形成环境。论述了如何通过密度—速度图分析，来限定地壳成分，尤其是下地壳的成分和变质程度。

重力模拟 密度—速度关系 联合解译 陆壳 前寒武纪 乌克兰地盾

引言

折射及广角反射与重力数据联合解译的主要条件是1960年代（Birch，1961）就已建立并被全球大量岩石密度和地震速度的实验室测量所证实的地震波速度与密度的相关性（Carmichael，1989；Henkel et al，1990；Krasovsky，1981；Christensen and Mooney，1995）。通常，这些早期的密度—速度关系的研究，旨在获得与不同围压和温度下不同岩石层岩石密度和速度实验室测量结果近似的线性和非线性回归曲线。这些曲线被用来重算由广角反射和折射实验产生的地震波速度模型，从而得到密度模型。

尽管有关密度—速度相关性的研究很多，但它们却极少专门用来分析属不同构造和地质年代的各地质单元的此类相关性。Krasovsky（1981）认为，全球范围内与实验室测量的密度—速度关系大致相符的回归曲线与那些和局部地区数据基本吻合的回归曲线之间的差异是对全球不同地质区域的响应。

除了实验室测量之外，局部岩石层单元的密度—速度关系还能够直接从大尺度地震实验和观测的重力数据提供的岩石层内的速度分布得到，如见Kozlovskaya和Yliniemi（1999）、Kozlovskaya等（2001a，b；2002）。该方法能够发现使观测重力数据与密度模型耦合程度最佳的密度—速度关系，也就是，通过反演重力问题的途径得到密度—速度关系。

在东欧克拉通（EEC），通过可用的广角反射和折射剖面，用该方法研究了大尺度地质单元的密度—速度关系的变化：芬兰地区的SVEKA 剖面（Kozlovskaya and Yliniemi，1999）和EUROBRIDGE'95－97 剖面（Kozlovskayaet al，2001a，b；2002），这些剖面横跨了芬兰、立陶宛、白俄罗斯和乌克兰不同地质年代的一系列构造单元。对这些剖面得到的密度—速度关系基本上是准线性的，并且说明围绕相应密度值的P波速度的散射适中。而散射则源于不同构造单元的密度—速度关系的变化。该研究同时揭示了密度—速度关系在背离准线性关系时的一些例证。正如 EUROBRIDGE'96剖面（Kozlovskayaet al，2002）所说明，密度—VP关系由于构造变形岩石所组成的地质单元，在其内部形成大尺度地震各项异性的影响使之背离一般关系。这种背离准线性密度—VP关系的现象也见于某些大规模环斑－辉长－斜长岩地块，因其含有丰富的高长石矿物的岩石，如环斑花岗岩和斜长岩。广角反射和折射剖面横跨这样的地块时显示在上地壳深度P波速度非常高（最快达6.4km/s）。有时地震波高速区域却为负重力异常区，如横跨维堡的环斑岩岩基波罗的海剖面（Luosto et al，1990）和横跨乌克兰地盾的科罗斯坚拉斑－辉长－斜长深成岩体的EUROBRIDGE'97 剖面（Thybo et al，2003）。然而，假若采用任意常规的密度—VP关系重算这些高速区的密度，可见其显示的计算重力作用结果应为正值。

本文论述了如何通过P波和S波两个速度模型和密度的关系计算密度以解决上面的问题。我们应用来自EUROBRIDGE'97广角反射和折射剖面的地震和重力数据，包括布格异常与P波和S波速度模型（Thybo et al，2003）。本项研究另一个目标是通过比较EUROBRIDGE'97剖面地震波速度和密度与岩石学数据，解释横跨该剖面不同构造单元的密度与速度之间的差异性。

1 地震和重力数据联合反演主要条件的密度—速度关系

1.1 来自岩石弹性性质实验室研究的密度—速度关系

岩石密度和压缩波速度的关系最初是由Birch（1961）获得的，其限定压力上限为10kbar（千巴）并假定各向同性介质中的压缩波速度VP主要取决于两个参数，即平均原子质量mA和物质密度d：

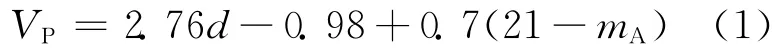
（1）式中的平均原子质量mA是表征岩石组分的另一个参数。Anderson（1967）用自己的方法研究证明了Birch得出的主要结论，即地震波速度、密度和平均原子质量之间是相关的。他认为密度由压缩波和剪切波速度得到，并得出了密度—地震波速的关系式：

式中VS指各向同性介质的剪切波速度，Φ是地震参数，a是系数，指数n为一个可取1/4或1/3的量。按 Birch（1961）已注明的富含钙质斜长石的岩石具有较高的P波速度而不满足常规密度—VP关系。Simmons（1964）对Birch（1961）关系进行了修正，其将CaO含量的影响考虑了进去。而后，Manghnani等（1974）得到了压缩波和剪切波速度的相似等式：

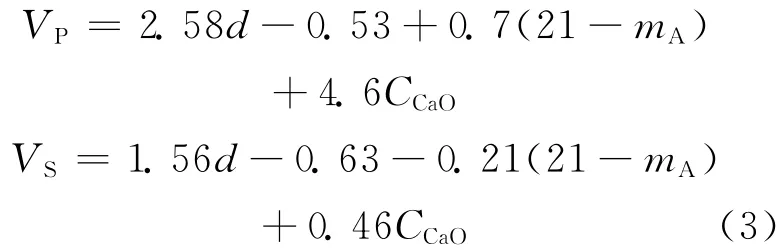
（3）式说明平均原子质量和CaO含量对剪切波速度的影响弱。由此可见，各向同性介质S波速度与密度的相关性较之P波速度更强。

此后，在实验室条件下得到的以及来自不同地质区、不同压力和温度条件下的各种岩石类型的钻孔测试得到的速度—密度的结果已编录成大量的密度—速度关系。关于这些结果的详细分析的论文有：Krasovsky（1981）、Barton（1986）以及 Schön（1998）。从这些文章中可见，在多数常规状况下，压缩波速度与密度关系对地壳岩石而言是与线性回归曲线近似的。一个在广角反射和折射数据与重力数据联合反演中应用最为广泛的密度—速度关系曲线是 Nafe－Drake曲线（Ludwiget al，1970）以及由Christensen和Mooney（1995）得出的压缩波速度和密度的关系。

应用这种密度—速度关系的一个显著的难点是对所揭露的所有岩石层岩石类型常常出现围绕其平均值发生明显散射现象。而KTB超深钻孔的密度—速度关系研究说明，密度—速度关系的统计特性与观测范围呈强相关性（Kneib，1995；Goff and Holliger，1999）。在短波区间（小于10m），由于大的散射影响，记录的速度和密度间的相关性非常差，而随波长变大，该相关性变强（散射减弱）。这意味着对于大于10km特征尺度的地质单元，密度—速度关系的散射现象明显小于实验室岩石样品测试的散射。因此，我们认为对于数十及数百千米特征尺度的岩石层单元的广角反射和折射调查区，其密度—速度的相关性是很强的。

1.2 大陆岩石层中密度和压缩波速的相关性

大陆岩石层中，地震速度和密度受压力和温度条件以及岩石的宏观和微观结构、裂隙和节理，还有流体和构成岩石各种矿物的各向异性的影响。总体来看，这些因素都以各自不同的方式在微观或者宏观尺度上对密度和速度产生作用。因此，岩石层研究中，在处理大尺度的数十千米深度的地质单元时，这些因素并非都要考虑。

上地壳中，影响地震速度的主要因素包括裂隙和节理的存在，以及其间常充填的流体。超深钻的岩石属性的精细研究说明，深度下达至少10～12km的上地壳都存在含流体的节理和裂隙穿插（Ganchinet al，1998；Smithsonet al，2000）。据此，地震波在上地壳中的传播速度将低于固有（无裂隙）速度约0.2km/s（Smithsonet al，2000）；因此以这些速度为基础的任意线性密度—速度关系计算得出的密度值，也许系统地被低估了。

中下地壳的岩石裂隙紧密，地震波速和密度取决于压力和温度，但是较之岩石组分影响这些因素则显得微弱。在低热流区，压力与温度对地震速度和密度的综合效应，在中下地壳对应的深度（即压力超过2kbar）时消 失 （Kern and Richter，1981；Schön，1998）。因此，在中下地壳的深度，速度和密度都主要取决于岩石的矿物组分的弹性性质，并受控于压敏性（由压力变化产生的矿物——译注）矿物反应形成的矿物集合体，即岩石组成由富长－贫石榴子石到富石榴子石－贫长石的变化（Green and Ringwood，1967）。密度与地震速度随深度增加而增加，同时密度与P波和S波速度相关性也更强（Sobolev and Babeyko，1994）。从芬兰的SVEKA剖面（Kozlovskaya and Yliniemi，1999）以及EUROBRIDGE'95—EUROBRIDGE'97剖面（Kozlovskayaet al，2001a，b；2002）等区域得到的岩石层单元密度与P波速度的关系与Sobolev和Babeyko（1994）的密度—VP曲线大体相符，而这一关系在不同构造单元的变化则导致了P波速度围绕相应的密度值的散射（0.2～0.5km/s）。我们还发现，在一些构造单元我们所得到的密度—VP关系与常规关系相背离。如横过EUROBRIDGE'96的中白俄罗斯地带，密度—VP关系线性就因构造变形的岩石的各向异性（Kozlovskayaet al，2002）而背离常规关系。另一个构造单元是科罗斯坚拉斑－辉长－斜长非造山带岩体（科罗斯坚深成岩），在那里EUROBRIDGE'97剖面揭示上地壳的P波速度较高（Thyboet al，2003）。高速P波区显示的是负重力异常。然而，该剖面的重力模拟表明按任意准线性密度—VP关系均难以解释负重力现象。

科罗斯坚深成岩主要由两类岩石组成，即环斑花岗岩和辉长－斜长岩。因此，在地壳顶部高P波波速和相伴的负重力异常可作斜长岩解。由于含有大量斜长石和CaO，这些岩石具有与辉长岩相当的高P波波速，而其密度则明显偏小（Henkelet al，1990；Kernet al，1993）。但是斜长岩的平均密度大约在2.7g/cm3，这样的密度对于解释该负重力仍然是过高的。

对高P波波速和负重力的另一种解释认为，与其他花岗岩类不同的是低密的环斑花岗岩的P波速度受压力的影响更大。在限定与今天地温相应的压力和温度条件下，Lebedev （1989）、Lebedev 和 Korchin（1982）、Lebedev等（1972，1983，1990）对乌克兰地盾花岗岩弹性性质进行了大量详尽的实验室研究。基于这些成果，Schön（1998）认为花岗岩类的P波速度与岩石的结构密切相关。研究发现粗粒环斑花岗岩的VP速度受压力影响最大，其VP从地表的大约6.0km/s至大约5km深度迅速升高到6.5km/。而对于细粒和中等粒度的花岗岩而言压力对VP的影响要小得多。

在环斑花岗岩中，由于压力对P波速度的影响是非线性的，因而如果仅用P波速度，就不能识别更大密度的斜长岩。与P波不同，实验室研究表明环斑花岗岩和斜长岩中的S波速度，在同等深度间隔的情况下，总体受压力的影响更小。由公式（3）可得出下面的结论：S波速度受高斜长石含量的影响也较小。这说明基于P波和S波两者的反演更有利于获得更接近实际的密度模型，与观测重力数据的耦合度也更好。

1.3 剪切波速度与密度的关系

与更加常见的密度—VP关系一样，密度与剪切波速度之间经历了大量实验室研究，得到了与实验室测量结果相近的关系（如见，Gebrandeet al，1982；Dortman，1992；Schön，1998）。

Gebrande等 （1982）和 Manghnani等（1974）认为，各向同性的剪切波速度主要取决于岩石密度，而mA对其影响微弱。这些研究也表明，各向同性VS受CaO含量的影响也较VP更小，对此可见公式（3）。

Rosental（Dortman，1992）得到了与岩石层岩石的VP、VS和密度关系相近的线性回归：

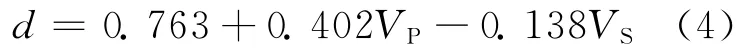
Khalevin等（1986）也得到了压缩波和剪切波速度与密度关系的非线性回归：

密度与VS速度的关系或者密度与VP、VS两者的关系很少用于地震与重力数据联合反演研究，其原因在于广角反射和折射调查通常是基于P波解译的。而根本在于S波的接收质量较差，其被P波的尾波所掩蔽。这使得获得S波速度模型变得很困难。但是在地盾区，由于缺失厚沉积物，广角反射和折射数据中的S波质量与P波相当。在这样的地区，我们可以得到独立的S波模型。因此P波和S波速度都可以用于重力建模。Kozlovskaya和Yliniemi（1999）在研究芬兰的SVEKA剖面时采用了基于这一密度与VP和VS关系建立重力模型的方法。本文中，我们应用相同的手段获得EUROBRIDGE'97剖面的密度模型，并分析在横跨该剖面的各地质单元中密度与VP和VS间的关系。

2 EUROBRIDGE'97广角反射和折射剖面地震P波和S波速度模型

2.1 EUROBRIDGE'97广角反射和折射实验

地震实验是EUROBRIDGE计划的一个组成部分，其目的是为了建立波罗的海与乌克兰地盾元古代和太古代裸露杂岩下的东欧克拉通岩石层深部结构模型（Bogdanova et al，1996a）。之前已完成了总长1200km的三段陆上剖面的深地震探测：1995（EUROBRIDGE Seismic Working Group，2001）、1996 （EUROBRIDGE Seismic Working Group，1999）和 1997（Thybo et al，2003）。EUROBRIDGE'97调查由白俄罗斯、乌克兰、英国、丹麦、芬兰、德国、波兰和瑞典等研究机构间的国际合作完成。1997年8、9月间，于东欧克拉通萨尔马提亚（东欧地区维斯杜拉河和伏尔加河之间地区——译注）沉积区完成了530km南北走向剖面的地震数据采集（Thybo et al，2003）。EUROBRIDGE'97横跨萨尔马提亚岩层，尤其值得注意的是在科罗斯坚深成岩附近获得的较高分辨率数据。EUROBRIDGE'97地震调查的详细情况见Thybo等（2003）的描述。

EUROBRIDGE'97北部剖面位于萨尔马提亚部分地壳西北边缘附近的奥斯内斯克—米卡舍维奇火成岩带（OMIB）内。奥斯内斯克—米卡舍维奇火成岩带大约有100～150km宽，由不同组分元古代火成岩构成，整体未经历区域变质作用。杂岩主要成分为闪长－花岗闪长－花岗岩和石英－正长－花岗岩以及变辉长－辉绿岩（2.1～2.0Ga）。奥斯内斯克—米卡舍维奇火成岩带局部有普里皮亚特地槽和沃伦—奥尔沙大陆裂谷（Bogdanova et al，1996b；Claesson et al，2001）的沉积物覆盖。

普里皮亚特地槽（PT）是显生宙普里皮亚特—第聂伯—顿涅茨克古裂谷的一部分（Stephenson et al，1996）。普里皮亚特地槽大约长280km，宽150km，被局部厚度达6km的沉积物充填。厚200～300km的中泥盆世陆源和碳酸盐岩层为其最老的地层。分布最广的地层时间从上泥盆世至中泥盆世，含有陆源沉积岩、碳酸盐岩、盐岩和火山碎屑岩。它们组成了几千米厚的地层，而最新的上三叠世至第四纪地层厚度仅有150～200m（Aizberg et al，1987）。

沃伦地块（VB）完全由元古代岩石构成。古元古代片麻杂岩出露于沃伦地块的南东和南西部，其发生了角闪石相到绿帘－角闪石相变质作用，地层的年代介于2.2～2.1Ga（见 Stepanyuk et al，1999；Bogdanova et al，2004）。这里代表性的岩石为南部和北部块体的重熔花岗岩（2.06～2.02Ga）以及沿深断裂形成的多种成分的侵入杂岩（2.02～1.98Ga）（Shcherbak et al，1989；Skobelev et al，1991）。橄榄岩－辉岩－辉长岩、橄榄岩－橄长岩－斜长岩、碱性超基性岩、苏长辉长岩－二长岩、辉长岩－正长岩－花岗岩和花岗闪长－花岗岩集合体都已得到区分（Skobelev et al，1991）。

科罗斯坚深成岩体（KP）是一个独特的局域显著分层的环斑－辉长－斜长岩非造山深成杂岩（1.8～1.74Ga），局部厚达6km，其下地壳发生广泛的铁镁质岩浆上侵。科罗斯坚深成岩体主要由环斑花岗岩、辉长－斜长岩和苏长辉长岩组成（Lichak，1983；Verk－hogliad，1995）.。

波多利地块（PB）位于西乌克兰地盾南部。其最古老的地质单元（＞3.4Ga）是由紫苏花岗闪长铁镁质麻粒岩和紫苏花岗闪长－片麻岩组成，呈侵入状态（Shcherbaket al，1989；Lesnayaet al，1995）。古元古代该区经历了强烈的构造运动、变质作用和重熔过程，形成了多种重熔花岗岩类（2.08～2.02Ga）（Shcherbaket al，1989；Skobelevet al，1991；Lesnayaet al，1995）。这些岩石在北部接近沃伦地块的地区广泛分布。

2.2 EUROBRIDGE'97剖面地震速度模型

通过P波的初至波层析成像反演获得了初始二维 P 波速度模型（Thyboet al，2003）。应用SEIS83射线追踪软件包及MODEL和 XRAYS软件（Komminaho，1998）支持下得到了最终深度达80km的岩石层二维模型，1983）。在射线追踪过程计算得到理论走时，并将其与观测走时比较，而后相应地调整模型参数关系直至得到观测和模型反演走时的吻合度在0.2s的合理模型。另外，在地震测线边界，通过计算合成地震图来控制各层的速度梯度和地震边界的速度差。图2a是沿EUROBRIDGE'97剖面的最终精细速度模型（Thyboet al，2003）。

由P波速度模型可见，该区地壳在空间上分别与奥斯内斯克—米卡舍维奇火成岩带、沃伦地块、波多利地块和科罗斯坚深成岩体相关联，波速度的横向变化显著。地壳厚度大约45km，南部地区有轻微的增加，最厚达50km。

深度10～15km的上地壳结构是最为复杂的。在该剖面北部和南部，结晶地壳的速度值约在6.1～6.2km/s。而与普里皮亚特地槽厚沉积物对应的剖面北部地区，其下大约4km为低速度层（2.4～4.2km/s）。在剖面南部10～12km深度存在速度值约6.1km/s的弱低速层。中地壳由两个层组成，其速度分别为 6.4km/s和 6.7km/s。地壳最下部以7.0～7.4km/s波速为特征。地壳底部，尤其在剖面中部的沃伦地块区下，具有7.4km/s超高速度的复杂结构。莫霍面下的速度在剖面南部为8.3～8.4km/s，中部则为8.1km/s。另外，在剖面中部莫霍面下已发现倾斜反射界面。

观测折射和反射S波的垂直分量记录用于分析EUROBRIDGE'97剖面S波波至的关系（Thyboet al，2003）。整体来看，剖面南部的观测S波数据更强，也更清晰。而北部，最大距离200km S波波至数据相对于背景的P波尾波往往非常微弱。

拾取的S波走时的数据集有限，不满足建立独立S波速度模型的条件。因而，对于普里皮亚特地槽，VP/VS比采用 Molotova和Vasiliev（1960）对该区沉积岩精细的实验室研究得到的关系，并利用最佳的互相关S波走时曲线估算出结晶地壳主要分层的VP/VS比。图2c是EUROBRIDGE'97剖面下岩石层内VP/VS的分布图。通过该分布图，并利用图2a中的P波速度模型计算得到初始S波速度模型。最终的S波速度模型（图2b）是通过试错法反复交互式的调整得到与观测的折射和反射S波走时耦合最好的模型。

上中结晶地壳中VP/VS比（图2c）在1.68～1.78之间变化。模型中部下地壳的两个主要分层和上地幔的P波速度分别为7.1、7.4～7.6和8.35km/s，而S波速度则分别是3.95、4.25～4.45和4.55km/s（图2b）。这里得到其对应的下地壳两个主要分层的VP/VS比为1.78和1.71～1.74，而上地幔为1.84。

在模型中科罗斯坚深成岩体的上中地壳的VP/VS较其邻区（1.77～1.84）整体具有更高的比值，而波多利地块则具最低VP/VS比值。

图2 沿EUROBRIDGE'97剖面二维P波（a）和S波（b）速度模型以及VP/VS 比（c）（Thybo et al，2003）。粗黑线表示由反射或/和折射的P波或/和S波约束得到的主要速度不连续面（界面）；细线表示速度等值线；各种颜色（原图为彩色图——译注）代表VP/VS的比值分布

3 沿EUROBRIDGE'97剖面的密度模型

3.1 重力数据

本研究所用的重力数据包括沿EUROBRIDGE'97剖面的布格异常及重力的长周期区域分量（图3a）。数据来源为白俄罗斯国家科学院地球科学研究所根据在白俄罗斯和乌克兰的重力测量结果所绘制的相应数字重力图 （Garetskyet al，1991；Egorovaet al，2003）。重力场的区域分量通过Karatayev（1996）的非线性滤波技术计算得到。

由图3a可见，沿EUROBRIDGE'97剖面区域性重力低在空间上与普里皮亚特地槽相耦合。然而仅覆盖该剖面北部的厚沉积层的作用能解释这一现象，其中普里皮亚特地槽的北翼为观测布格异常的水平梯度高的区域（图3a）。在普里皮亚特地槽的南部，重力场比较缓慢地向南增大，在剖面约350～450km间出现清楚的区域极大值。局部的趋势是上地壳密度变化导致的几个较小振幅的重负异常的叠加的效果。

观测的覆盖科罗斯坚深成岩体的重力场的形态不是 “典型”的环斑－斜长岩岩基圆弧形负异常，如芬兰的维堡环斑岩体的观测结果（Elo，1997）。科罗斯坚深成岩体是一个由多期次上侵的属几个大的地质单元的各种复杂的具明显密度差异岩石组成的杂岩体（花岗岩和辉长－斜长岩）。因此重力效应是不同强度的正负异常综合的结果（图3a）。科罗斯坚深成岩体的布格异常从普里皮亚特地槽的接近－60mGal到科罗斯坚深成岩体南部的＋20mGal。在科罗斯坚深成岩体的北部（190～275km）为该区主要的负异常区，其部分是由普里皮亚特的厚沉积造成的。普里皮亚特地槽的南边，即模型218km处可见显著的布格异常的极小值。局部异常在空间上与奥夫如奇地槽沉积物充填有关。剖面的更南边在科罗斯坚深成岩体的西南部，那里的重力场以沃洛达斯科―沃林斯基斜长岩岩体形成的负重力作用为主。EUROBRIDGE'97剖面的二维重力模型正演结果见Egorova等（2003）的描述，其认为如果用密度—VP标准线性关系重新计算VP与密度的关系，则重力极小值位于科罗斯坚深成岩体北部是不合适的。

3.2 EUROBRIDGE'97剖面重力数据的反演

本文EUROBRIDGE'97剖面的二维密度模型（图3）是由P波和S波速度模型（图2）应用Kozlovskaya和 Yliniemi（1999）的重力数据反演方法得到的。该方法基于VP、VS和密度间的非线性关系，其与Khalevin等（1986）及公式（5）相似。根据这一公式，我们认为二维剖面密度和地震波速关系可近似表达为如下的函数：

式中：U0（x，z）＝1，U1（x，z）＝VP（x，z），U2（x，z）＝VS（x，z），U3（x，z）＝VS（x，z）VP（x，z），U4（x，z）＝V2P（x，z），U5（x，z）＝V2S（x，z），U6（x，z）＝1/VS（x，z），U7（x，z）＝VP（x，z）/VS（x，z）。函数Uj（x，z），j＝8…N，代表沿该剖面测量的额外的一些地球物理参数，这些参数反映了研究区不同岩石层块体的差异，也可以从地震模型中直接获得。这些函数引入到公式（6）使我们可以建立大尺度岩石层单元的各种密度—速度关系模型。这些函数可以是沿剖面的区域性磁场或者各种热流等。大尺度岩石层块体间的差异信息同样可从地震模型获得。

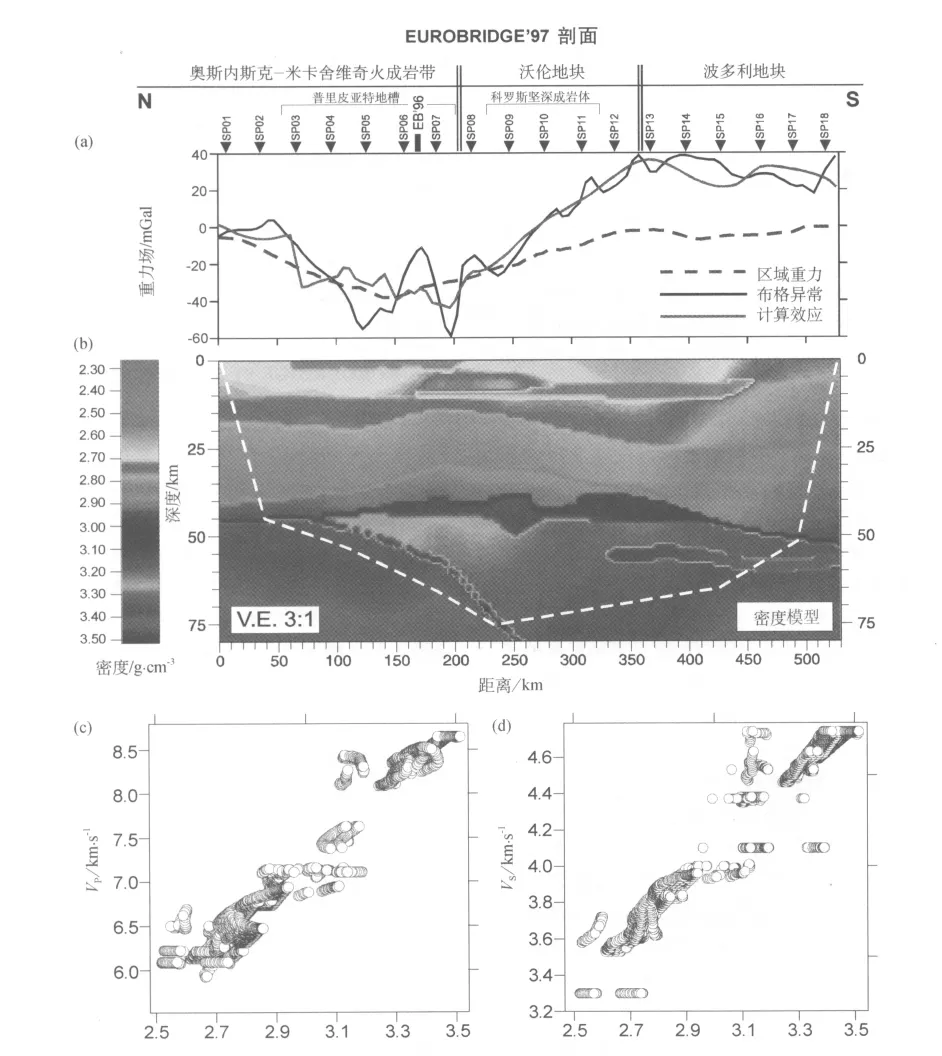
图3 沿EUROBRIDGE'97剖面由图2所示P波和S波速度模型计算的二维密度模型（原图为彩色图——译注）。（a）观测重力场（黑线）、区域重力场（蓝虚线）和二维模型计算重力效应（粉色线）的比较；（b）二维密度模型（虚线为地震模型的范围）；（c）和（d）由图2的P波和S波速度模型和图4b的密度模型得出的密度—速度图

如 Karatayev等（1993）和Christensen与Mooney（1995）所述，不同地质年代和演化过程的地质单元具有不同的地壳构造，即主要边界的深度（莫霍面、基底面、上地壳和中地壳边界、中地壳与上地壳边界）和平均地壳速度。剖面上大尺度的各地质单元的密度—速度模型参数也相应地发生改变。本文中，函数U8（x，z）＝VPmean（x）表示由图2模型z轴平均值得到的P波速度；U9（x，z）＝H1（x），U10（x，z）＝H2（x），U11（x，z）＝H3（x）表示由地震模型得到的3个主要地震边界，即基底面、上中地壳边界以及莫霍面。函数U12（x，z）＝H4（x）和U13（x，z）＝H5（x）表示由地震模型得到的2个额外地震界面，即中下地壳边界面和下地壳和高速层界面。密度—速度模型的变化情况可表示为U14（x，z）＝VPmean（x）VP（x，z）和U15（x，z）＝dVPmean（x，z）/dx。

公式（6）中系数Ak是未知的，其可由重力问题的反演方法得到，该方法可见Kozlovskaya和 Yliniemi（1999）的详尽阐述。公式（6）是在已知P波和S波速度模型的情况下，经对任意二维密度分布常规积分算子和数值积分来计算密度分布。为此，速度—密度模型需通过规则矩形网格进行参数化。该研究中我们采用2×2km的正方形网格，满足表示主要间断面的密度和速度梯度。

图3c和3d为重力反演结果，表达了EUROBRIDGE'97剖面密度—速度关系。图中给出了由二维速度密度网格中提取的密度值和其相应的速度。可见通过该方法使我们建立了与实际岩石实验测量结果相近的非线性和离散密度—速度关系模型。

图3a表明，由密度模型计算的重力场与EUROBRIDGE'97剖面观测布格异常除剖面端元外，均十分吻合。剖面的北部端元重力场主要受普里皮亚特地槽厚沉积物的影响，因此重力建模需要详细的沉积盖层的结构信息。虽然普里皮亚特地槽的速度结构有前期该区地震调查（Thyboet al，2003）的约束，但是沉积盖层的内部分界仍需进行平滑处理以适应SEIS83射线追踪的要求。而平滑处理也会将一部分精细的沉积结构丢失，这使得在普里皮亚特地槽的模型曲线与实际观测的布格异常的拟合较差。

普里皮亚特地槽下的地壳密度值与此前EUROBRIDGE'96剖面重力模拟获得的结果（Kozlovskayaet al，2002）相符。上部结晶地壳，即深度5km处的密度值与EUROBRIDGE'97剖面主要地质单元岩石密度的先验数据（Egorovaet al，2003）高度拟合。与波多利地块位置相对应的剖面南部为该区已发现的上地壳最大密度。在剖面的中部，科罗斯坚深成岩体下地壳具有复杂的密度分布。高速下地壳（HVLC）的密度约为3.1g/cm3，而奥斯内斯克—米卡舍维奇火成岩带和波多利地块毗连区下地壳的密度约2.95～3.0g/cm3。模型同时也显示科罗斯坚深成岩体下的上地幔密度较低，地震数据可见其莫霍面倾向南。该层（HVLC）的密度约3.25～3.30g/cm3，而与其直接接触的莫霍面下毗连区的密度为3.35～3.40g/cm3。该结果可作为比较此地幔界面区域的岩石弹性学性质的另一个证据。该层与邻区上地幔的构造单元的密度对比说明，这种密度差别足以在普里皮亚特地槽和科罗斯坚深成岩体区南部产生与重力场的局部趋势相一致的负重力效应。

4 EUROBRIDGE'97剖面所跨不同地质单元的密度—速度关系

图3b和3c分别为由重力数据反演得到的密度—VP和密度—VS的关系。纵观EUROBRIDGE'97剖面的密度与VP的关系可见其由一些分支组成，而不能拟合归纳成任何一种简单的线性关系。密度—VS关系表明有相同的特征，尽管其密度域在2.5～3.0g/cm3的散射较密度—VP关系的要小。EUROBRIDGE'97地震剖面揭示出密度大于3.2g/cm3的上地幔岩石中密度—VP与密度—VS的关系均由两枝组成，它们对应上地幔的不同速度值（图2）。

图4 横跨EUROBRIDGE'97剖面的大地质单元密度、VP和VS间的关系。（a）奥斯内斯克―米卡舍维奇火成岩带，（b）波多利地块，（c）沃伦地块和科罗斯坚深成岩体。左侧图为密度—VP的关系，右侧图为密度—VS的关系（VS的轴用1.73标定）。五角星表示参考密度—速度关系

为理解密度—速度关系的散射现象，我们分别绘制了垂直该剖面的3个主要构造单元的关系图。分别从与奥斯内斯克—米卡舍维奇火成岩带、沃伦地块以及科罗斯坚深成岩体和波多利地块区域相应的二维速度和密度网格中提取密度值与其对应的速度值。该研究不包括普里皮亚特地槽的沉积岩。结果见图4，这里说明的是上述3个构造单元的密度—速度关系，左侧图为密度与VP的关系，右侧图为密度与VS的关系。从图中可见，在这些单元中密度—VP与密度—VS的关系是不同的。考虑到剖面所在区域为低热流区，因此较之不同岩石组分对影响密度和速度的影响，压力和温度的作用是次要的。这样对于奥斯内斯克—米卡舍维奇火成岩带、沃伦地块/科罗斯坚深成岩体和波多利地块间密度—速度关系的差异，可以解释为岩石组分的变化，即比较某一关系所对应的岩石的已知的化学和矿物组分。但是从实验室获得的岩石样品的密度—速度关系受其他因素影响，如裂隙和孔隙度，这些都可能混淆组分的作用效果。为排除非岩石因素的影响，假设特殊组分矿物的弹性刚度模量和密度已知，可采用模态矿物学的方法计算密度和速度。

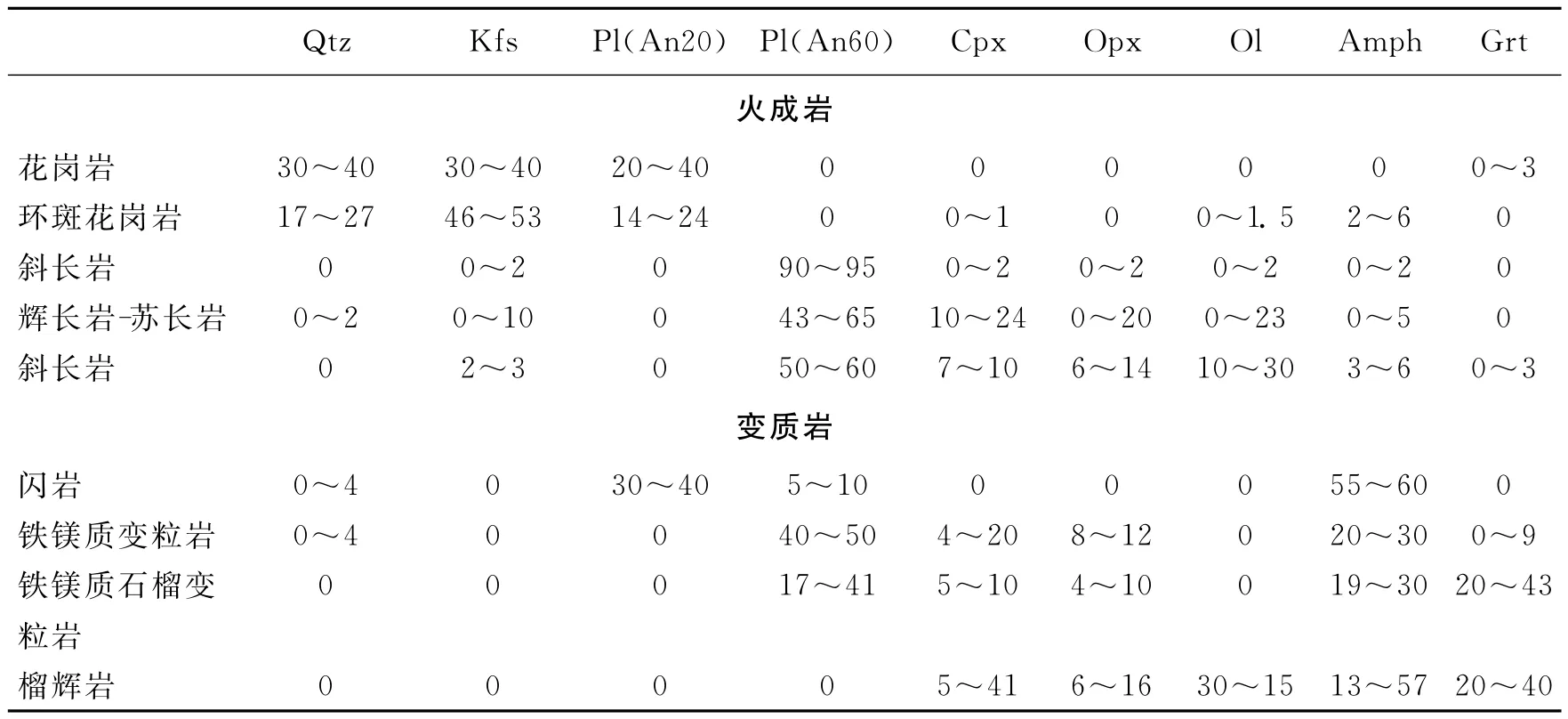
表1 模拟所用岩石类型的模态矿物成分（%）。Pl的An在括号中给出

4.1 蒙特卡罗法对已知组分岩石的地震波速度和密度的模拟

我们挑选了能够代表该区主要地壳岩石并包含不同性质的主要成岩矿物的岩浆岩和变质岩进行计算。挑选岩石的模态矿物学特征来自乌克兰地盾和其他前寒武纪地区的岩石学研究（Kozlovskayaet al，2002；Hurichet al，2001；Lichak，1983；Markwick and Downes，2000； Markwicket al，2001），并用其来估算每个岩石类型中主要矿物的模态比的范围。矿物学数据归纳为表1。而后对通过蒙特卡罗模拟估算出地震波速度和密度，其中每种岩石类型产生1000个随机结合的矿物模态比。Belikov等（1970）方案改进了 Voigt（1910）的均匀应变方法。我们应用Belikov方案根据一定空间压力和温度的模态矿物来计算弹性学参数。该方案的具体描述亦可见Schön（1998）。主造岩矿物的弹性劲度模量来自Dortman等（1992）。由蒙特卡罗模拟法得到的密度—地震波速度关系见图5。

图5a的密度—VP关系与 Hurich等（2001）的结果十分吻合。Hurich等（2001）分析了不同矿物对加拿大格林维尔省的岩浆岩和变质岩的密度和P波速度的影响，其没有分析S波速度问题。图5展示了不同密度—速度关系对应的不同模态矿物学结果，但是它们的趋势是相似的。为解释矿物对密度—速度关系的影响，我们必须将我们计算的结果与一些参考曲线作比较，即未经过变质的岩石的平均化学组分与密度—速度关系。Sobolev和Babeyko（1994）得到了一些可代表主要地壳岩石的具有不同平均化学组分的无水岩浆岩的密度—速度关系，包括花岗岩、花岗闪长岩和辉长岩。在图5相应的密度—速度图中用五角星给出参考关系。从中可见，矿物成分对密度—VP关系的影响总体强于密度—VS关系。

对计算密度—速度关系与参考曲线进行比较（图5a，b）可见，富含钙长石而贫角闪石的岩石（即斜长岩、辉长－苏长岩和辉长岩）的密度—VP关系与参考曲线正偏移。然而富含钙长石对斜长岩的密度—VS关系无明显影响，其与参考曲线十分接近。在一般斜长岩的成分从拉长石向奥长石的变化以及花岗岩和环斑花岗岩中长石含量的增加使得这些岩石的密度—VP关系移向参考曲线下方，而相应的密度—VS关系与参考曲线却相当接近。受角闪石作用，密度—VP和密度—VS关系均与参考曲线呈负偏移关系，但密度—VP关系偏移更加明显。这一偏移是长石岩组分由拉长石向奥长石变化，同时长石总量减少而角闪石含量增加共同作用的结果。麻粒岩和铁镁质石榴麻粒岩，其包含的角闪石和富钙斜长石相对含量是一样的，而其密度—速度关系也与参考曲线接近。而在铁镁质石榴麻粒岩和榴辉岩中石榴石的增加与斜长石的减少都会使速度和密度较原曲线明显增大。铁镁质石榴麻粒岩的密度—速度关系与参考曲线具有相似的趋势，而榴辉岩中密度—速度关系则较参考曲线为正偏移，其可解释为榴辉岩缺失斜长石而富含辉石。

图5 对乌克兰地盾和其他前寒武纪地区所选火成岩和变质岩类型由蒙特卡罗模拟得到的密度与地震速度间的关系。（a）密度—VP关系，（b）密度—VS关系（VS的轴用1.73标定）。五角星表示参考密度—速度关系

综上我们认为，对密度—速度图的分析可用于约束地壳的组分，尤其是下地壳的组分和变质程度。因此与下地壳对应的一系列速度值中，如果密度—速度关系与参考曲线接近，就说明下地壳可能为铁镁质组分和麻粒岩相变质级的岩石。计算的密度—速度关系与参考关系的正偏离说明斜长石含量高且角闪石缺失，这种现象在火成岩中尤为典型。相反，负偏离则暗示下地壳更富含角闪石相岩石。若下地壳密度小于3.0g/cm3，说明下地壳含有高压和超高压石榴石相变的变质岩较少，即铁镁质石榴麻粒岩和榴辉岩为其次要组分，而如果下地壳的密度大于3.0g/cm3，则说明下地壳发生了高压条件下的变质作用且含有铁镁质石榴麻粒岩和/或榴辉岩。

4.2 EUROBRIDGE'97剖面的密度与速度的关系分析得出的地壳组分

EUROBRIDGE剖面横过的主要构造单元体的密度与速度的关系已经得到（图4a，b），其中参考密度—速度关系用五角星标出。奥斯内斯克—米卡舍维奇火成岩带的密度—速度关系在上中地壳与参考的曲线接近。而在下地壳深度则与参考曲线呈正偏移。这说明该处地壳主要由岩浆岩组成，其上部、中部以及下部分别主要为如花岗岩、花岗闪长岩和辉长岩的火成岩。

波多利地块的密度—速度关系的上中地壳同样也与参考曲线接近，而在下地壳则呈轻微的正偏移。这说明在波多利地块内，对于上中地壳而言，其由普通花岗岩－花岗闪长岩组分和低变质级岩石组成，而下地壳则为铁镁质组分和麻粒岩变质级的岩石。而在波多利地块，随着地壳厚度的增加使得下地壳的压力—温度条件达到发生榴辉岩相变的条件。尽管如此，此处下地壳的密度仍低于3.0g/cm3，表明石榴石为其次要组分且斜长石含量的增多暗示下地壳为经历榴辉岩化作用。这大概是波多利地块的厚地壳形成于无水条件时的情况（Austrheimet al，1997）。

沃伦地块和科罗斯坚深成岩体的密度—速度关系最为复杂（图4c）。图中可见计算的密度—VP关系与参考曲线是呈强烈发散的关系，并且它们之间既有正偏移又存在负偏移。这说明沃伦地块/科罗斯坚深成岩体的地壳的岩石组分及其来源都是不同的。然而，科罗斯坚深成岩体的密度—VP关系在地壳密度和速度范围内是近线性的。这便是尽管其上地壳具有高P波速度，而其与观测重力仍能较好吻合的原因。

密度—VP图中的正偏移区的密度小于3.0g/cm3，其对应科罗斯坚深成岩体的火成岩，即环斑花岗岩、辉长－苏长－斜长岩和辉长－苏长岩。斜长岩、辉长－苏长－斜长岩和辉长－苏长岩中斜长石的含量分别达到90%～95%，75%～85%和差不多50%（Lichak，1983）。

在密度—VP图中呈负偏移的点的速度和密度与上中地壳对应，其表示变质岩的存在。这些岩石和科罗斯坚深成岩体北部的高速体相联系，那里地震模型揭示出在5～12km深度有高VP和VS（分别为6.40～6.46km/s和3.66～3.72km/s）。高速体中的VS值异常高，不能单单由环斑花岗岩或者斜长岩解释。由密度模型（图3a）判断高速体的密度为2.75～2.80g/cm3。这种VP、VS与密度的关系可能是由富角闪石变质岩造成的（Lebedevet al，1983）。

科罗斯坚深成岩体的上部（0～5km）确定的VP、VS和密度的值说明，它们的组分为环斑花岗岩和斜长岩，但是深部地震探测数据的分辨率难以达到辨别精细构造。有一点是清楚的，即科罗斯坚深成岩体的确是一个复杂的且非匀一的地质体。

值得注意的是，计算的密度和P波速度与地壳顶部对应，其与参考曲线呈正偏移，而若按模态矿物学（图5a）计算的值则在其下。这是十分蹊跷的，因为科罗斯坚深成岩体的环斑花岗岩中钾长石的含量非常高，约为45%～50%（Lichak，1983）。因此这些密度和地震波速度值不能单单解释为组分差异。本文第二部分（第7页）已经提及，在粗粒环斑和似环斑花岗岩中VP受压力的强烈影响。岩石中VP从地表的6km/s至大约5km深度迅速增加到6.5km/s，而5～15km深度速度基本保持一致，在20km左右深度减小到约6.3km/s。这便可以解释图4中环斑花岗岩对应的密度—速度关系高于密度—VP的情况。

科罗斯坚深成岩体下的高速下地壳的密度值大于3.0g/cm3，说明它由铁镁质石榴麻粒岩组成。然而在高速下地壳对应的密度和速度范围内密度—VP关系高于参考曲线。这可能是斜长石含量较高压麻粒岩（表1）高的反映。下地壳岩石的P波速度和密度值与挪威比尔根弧的格林维尔石榴麻粒岩相辉长－斜长岩地区的观测结果相近，其在Fountain等（1994）分类中归于辉长质麻粒岩相斜长岩。

5 结论

1.本研究表明，通过基于密度和P波及S波关系的广角反射和折射数据的联合反演能得到更符合实际情况的密度和模型，其较常规的仅仅基于P波得到的模型与观测的重力数据的吻合度更好。EUROBRIDGE'97剖面的密度模型的计算重力场与观测布格异常显示为良好的耦合关系，同时也解释了其主要特征。

2.EUROBRIDGE'97剖面获得的大尺度构造单元的密度与地震波速度呈近线性关系。然而，各构造单元间的密度—速度关系是离散的，它们之间存在差异并与参考的具一般化学组分无水岩浆岩的曲线是背离的。

3.密度—VP关系的离散度总体要高于密度—VS关系。这是因为VS受平均原子质量和高钙斜长石的含量的影响较小的缘故。

4.总体来看，横跨该剖面的个别构造单元的密度—速度关系间的差异性及与参考曲线的背离关系，可解释为这些单元体内地壳的不同变质程度和组分差异导致的主要造岩矿物的实际矿物组合比例的不同。

5.奥斯内斯克—米卡舍维奇火成岩带的火成岩随斜长石含量的增多以及少量的角闪石形成了密度—VP关系与参考曲线的正偏离。可见区域变质作用过程并未明显改变奥斯内斯克—米卡舍维奇火成岩带的地壳构造。

6.波多利地块的密度—VP关系与参考曲线十分接近，说明中上地壳为大致平均的花岗岩－花岗闪长岩组分和低变质级，下地壳为铁镁质组分和麻粒岩变质级。尽管地壳厚度变大，但波多利地块的下地壳却未发生榴辉岩化，表明波多利地块厚地壳形成于无水条件之下。

7.沃伦地块和科罗斯坚深成岩体的密度—VP关系最为离散和复杂，表明这里火成岩和变质岩共存。然而，沃伦地块/科罗斯坚深成岩体的密度—VP关系总体正偏移于参考曲线，可解释为有高的斜长石含量。科罗斯坚深成岩体的粗粒环斑和似环斑花岗岩区，密度—VP关系背离参考曲线是上地壳应力对VP的非线性作用的响应。

译自：Acta Geophysica Polonica.2004.52（4）：397～424

原 题：Density－velocity relationship in the upper lithosphere obtained from P－and S－wave velocity models along the EUROBRIDGE'97seismic profile and gravity data

（浙江省海洋水产研究所 薛 彬译；阮爱国校；吕春来复校）