客运专线动车组断电过分相影响仿真分析

曾 琼,高 杰

(中铁第四勘察设计院集团有限公司,武汉 430063)

1 概述

1.1 列车断电过分相

牵引供电系统通过设置接触网电分相装置,隔离来自电网的或不同相序的电源。为了防止相间短路事故和保障列车设备安全,一般采用列车断电过分相的运行方式,即通过控制列车主断路器的分合闸操作,实现前进方向上的第一个受电弓进入分相断电区前的可靠断电,在工作取流受电弓行驶出分相断电区后及时合闸,完成列车断电过分相。由于电分相的存在,动车组需要断电过分相,而电分相设置的位置,分闸区长度和分闸区坡度都会对动车组的运行时分、速度产生影响,目前在公开发表的学术期刊中未见有此类问题的研究,但电分相的影响又确实存在。其存在不仅对动车组的运行会产生影响,而且在一定条件下甚至会关系到高速铁路的行车安全,因此研究客运专线断电过分相对动车组运行的影响是非常必要的。

目前存在2种断电过分相模式,一种是自动控制的列车断电过分相,另一种是手动控制的列车断电过分相,手动控制的列车断电过分相方式只在自动控制的列车断电过分相系统故障或未投入使用时采用,重点研究自动控制的列车断电过分相对动车组运行的影响。

1.2 元胞自动机

元胞自动机模型作为模拟非线性复杂系统的一种有效工具,近年来在交通流的研究中得到了广泛应用,模型的时间、空间、状态均离散,规则简单,非常适合计算机模拟。元胞自动机模型在保留交通流这一复杂系统的非线性行为和其他物理特征的同时,更易于计算机操作,可以通过灵活的修改其规则以考虑各种实际交通状况[1]。

2005年,李克平、高自友等人[2-3]首次将NaSch模型[4]思想运用于轨道交通系统的列车追踪模型和轨道交通流特性分析中,提出了一种适用于轨道交通系统的元胞自动机模型,对车站附近的列车流进行了模拟,分析了列车流的追踪运行特性。同年,宁滨[5]用NaSch模型对轨道交通列车追踪运行问题进行了系统研究,包括基于三显示固定自动闭塞控制系统下列车追踪的元胞自动机模型、基于移动自动闭塞控制系统下列车追踪的元胞自动机模型和考虑了前车速度效应的移动自动闭塞控制系统下的元胞自动机模型,并分析了轨道交通流的特性,丰富了列车追踪运行与交通流特性分析相关的基础理论研究工作。

2006年,周华亮、高自友等[6]提出了一种用于模拟准移动闭塞系统下的元胞自动机模型,分析了轨道单元长度、发车时间间隔和初始延迟时间等因素对列车延迟传播的影响。2007年,李峰、高自友等[7]提出了一种用于模拟固定闭塞系统的元胞自动机模型,并应用此模型模拟了四显示固定闭塞系统下的列车延迟传播的交通现象。

元胞自动机作为研究交通流的重要工具,在轨道交通研究中已经取得许多重要的研究成果,同时也具有其他研究方法所无法比拟的优势,因此将在以上研究基础上,建立适合客运专线四显示自动闭塞系统的元胞自动机模型,从电分相设置的位置,入分相的初始速度,分相长度和分相所在线路坡度来研究断电过分相对动车组运行的影响。

根据《铁路客运专线技术管理办法(试行)》(TG/04—2009)第174条以及《关于规范客运专线接触网锚段关节点分相设置的通知》(铁集成函[2007]474号)要求,在动车组工作双弓间距200～215 m的前提条件下,客运专线宜采用无电区约为220 m、中性区段约为520 m的电分相；因此本文最小分相长度取为520 m。

2 四显示固定自动闭塞系统的元胞自动机模型

下面建立四显示固定自动闭塞系统的元胞自动机模型。模型是建立在NaSch模型[1]和文献[3]的基础上的。在此将轨道划分为L个元胞,每个元胞大小相同,记为i=1,2,…,L，每个元胞或者为空,或者被列车占据。列车速度取0～vmax之间的整数,这里vmax为列车行驶的最大允许速度。

轨道线路中列车更新规则如下:

步骤1 加速

(1)防护信号机为绿色

vn=min(vn+a,vmax)

(2)防护信号机为黄绿色

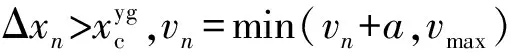
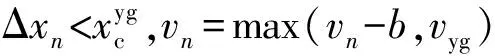
否则，vn=vn

(3)防护信号机为黄色

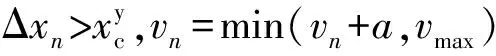
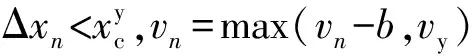
否则,vn=vn

(4)防护信号机为红色

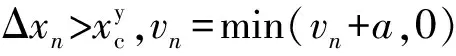
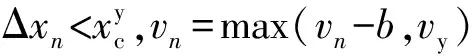
否则,vn=vn

步骤2 减速

vn=min(vn,gap)

步骤3 位移

xn=xn+vn

步骤4 更新信号灯的颜色

当B(k)=1

则color (k)=‘红’

当B (k+1)=1

则color (k)=‘黄’

当B (k+2)=1

则color (k)=‘绿黄’

否则color (k)=‘绿’

式中 Δxn——列车与前方防护信号机之间的距离；

xn——列车车头所在的位置；

vn——列车的速度；

a——列车的加速度；

b——列车的减速度；

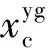
vyg——黄绿信号时列车的规定速度；

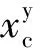
vy——黄色信号时列车的规定速度；

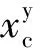
vmax——列车的最大限制速度；

gap——列车与前方目标点之间的距离；

B(k)——表示闭塞分区k的状态,1表示有车,0表示无车；

color(k)——表示k的信号灯颜色。

模型采用开放边界条件,定义如下：(1)初始时刻整个轨道全空,线路上无列车。系统每更新Ik次后,若系统第一个信号灯颜色为绿色,则在i=1处产生1列速度为vn的列车,该列车立即按系统更新规则进行更新。 这里Ik为列车的发车时间间隔。(2)若列车的位移大于L,即在i=L处,列车移出系统。为了使模拟结果与真实情况相符,在此规定每个元胞长度对应1 m,系统更新时步为1 s。也就是说如果vmax=69元胞/更新步对应的实际最大限速vmax=248.4 km/h。

使用上述模型对四显示固定闭塞系统的动车组运行进行模拟,分析不同入分相速度,分相长度和分相坡度情况下,电分相对动车组运行的影响。在此,假定轨道线路的长度L=180 000,闭塞分区长度BL=2 000,共9个闭塞分区,a=1,b=1,根据实际动车组长度一般不超过215 m,在此规定列车长度LT=215元胞。

3 断电过分相对动车组运行的影响分析

图1是分相在不同位置时的仿真结果示意,表1列出了不同分相位置对动车组运行时分影响,通过分析仿真结果,可以看到,电分相在前端位置时,由于动车组处于加速阶段,进入分闸区的速度较低,受分相的影响最大；分相在中部时,由于入分相速度较高,受到分相的影响也较小,而分相在后端时,动车减速进站,处于减速阶段,因此受到分相影响最小。图5(e),图5(f)是不同分相数量的仿真结果,由表1的数据可以看出,分相越多对列车的运行影响也就越大,但是由于图1(f)中最后一个分相在后端,对运行时分基本没有影响,从而造成了图1(e)和图1(f)的增加时分相同,综合以上分析,分相如果设置在动车加速阶段且动车入分相速度较低时,分相对动车组的运行时分影响最大,而分相如果设置在动车减速阶段且动车入分相速度较低时,分相对动车组的影响最小,因此在设置分相时应尽量将分相设置在动车减速阶段且动车入分相速度较低的位置,同时分相设置的数量应越少越好。

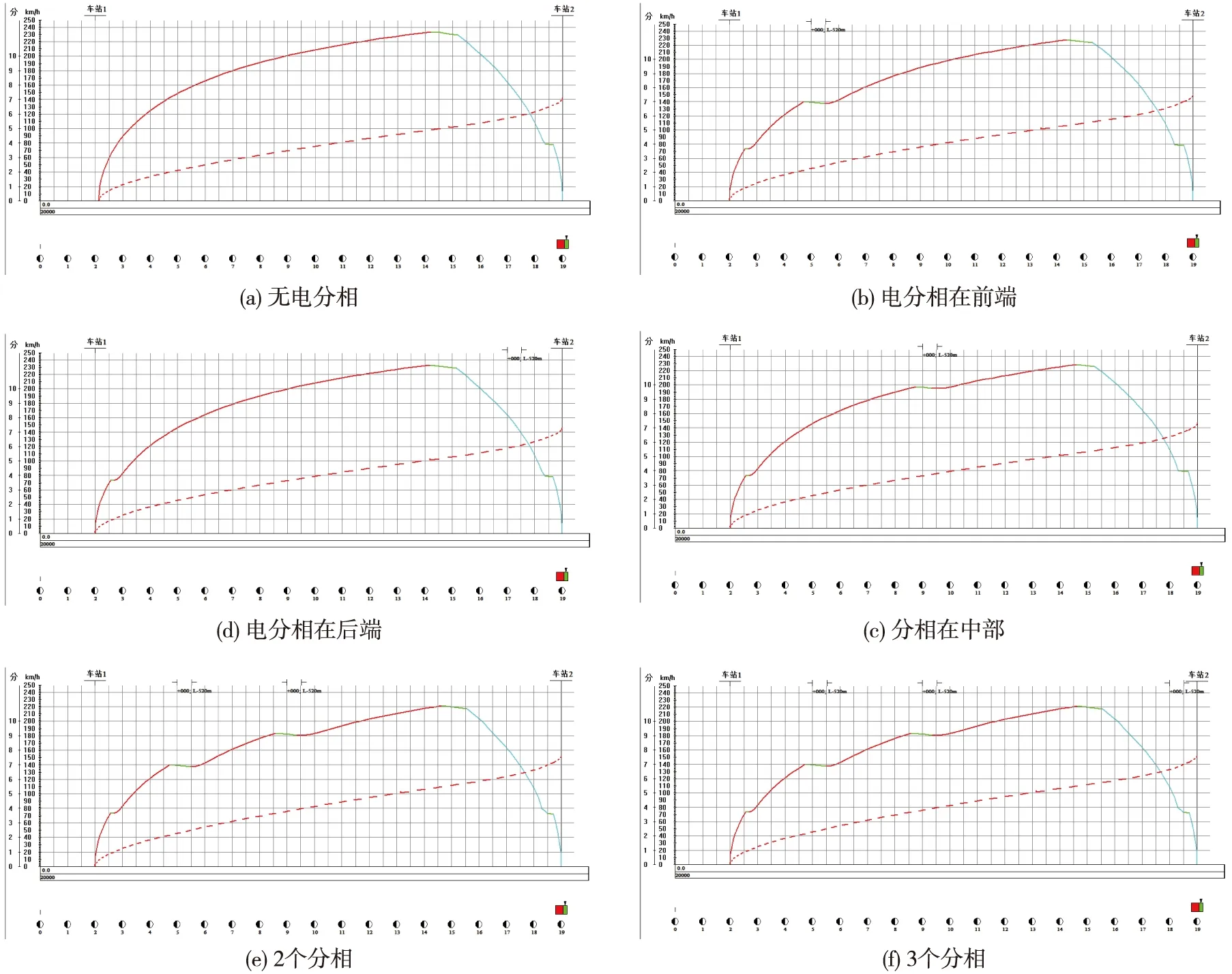
注：虚线表示时分-位移曲线,实线表示速度-位移曲线

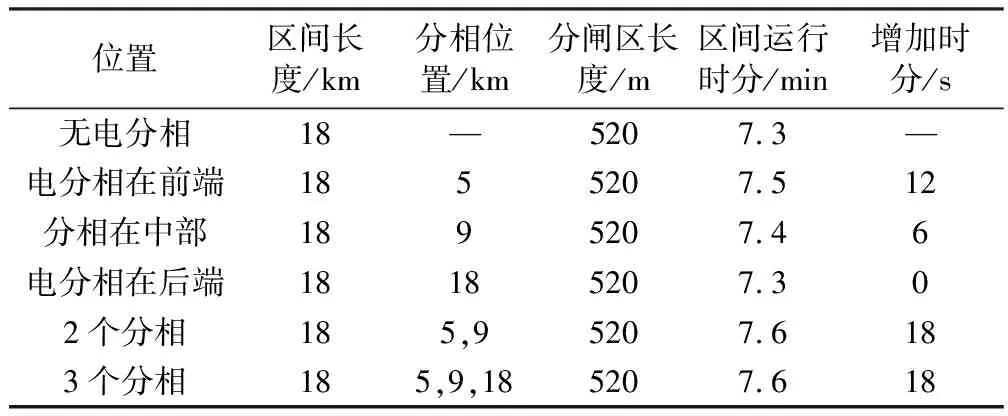
表1 不同分相位置对运行时分影响

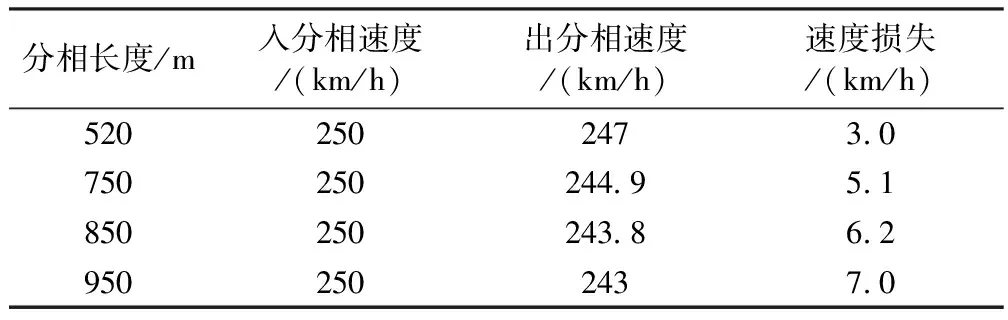
表2 分相位于0‰坡道仿真结果

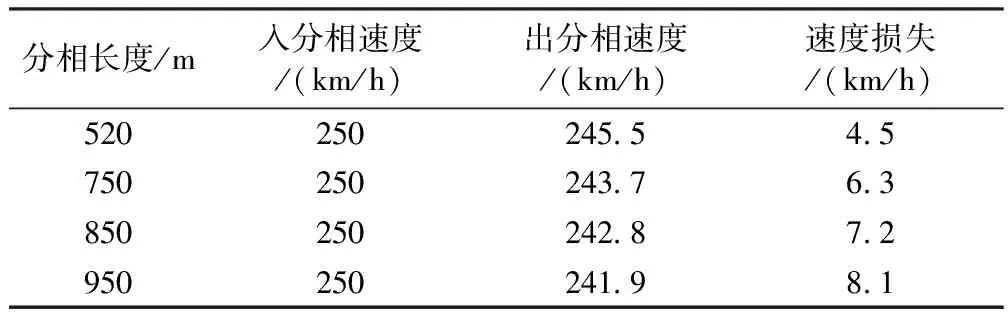
表3 分相位于10‰坡道仿真结果

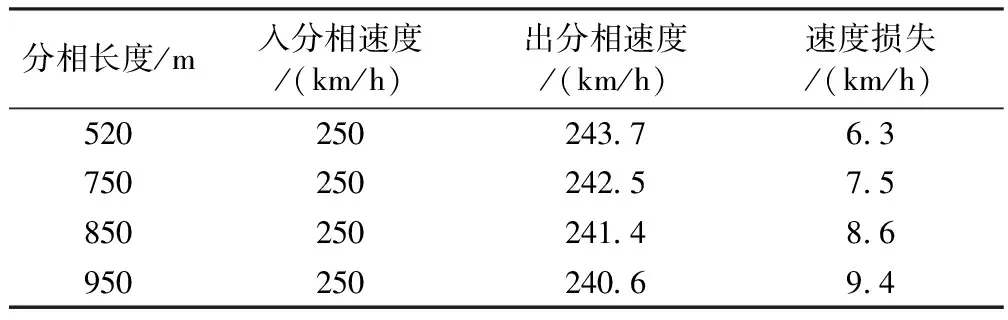
表4 分相位于20‰坡道仿真结果

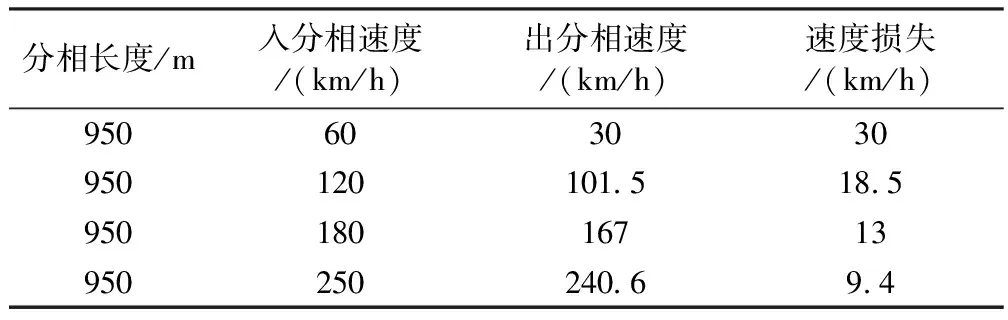
表5 分相位于20‰坡道仿真结果

表2～表4反映的是分相在不同坡道,不同分相长度时,对动车组运行速度的影响。分析仿真结果可以发现,随着坡度和分相长度的增大,动车组的速度损失也将随之增大。表5则是在最不利条件下,也就是坡道最大,分相长度最长的情况下,不同入相速度的仿真结果。由结果可以分析得出入相速度越低,速度损失也越大。因此在设置分相时,为了减少速度损失,确保列车能顺利通过分相而不在分相内停车影响行车安全,应尽量将分相设置在坡度较小,入相速度大的位置。在设计分相时,也应尽量考虑采用较短长度的分相。

4 结论

根据高速铁路的特点,提出了一种新的元胞自动机模型,并用来分析四显示固定闭塞条件下断电过分相对动车组运行的影响。在该模型的基础上,分析了不同分相位置对动车组运行时分影响,通过分析得出,分相如果设置在动车加速阶段且动车入分相速度较低时,分相对动车组的运行时分影响最大,而分相如果设置在动车减速阶段且动车入分相速度较低时,分相对动车组的影响最小,因此在设置分相时应尽量将分相设置在动车减速阶段且动车入分相速度较低的位置,同时分相设置的数量越少越好。同时通过仿真,分析了分相在不同坡道,不同分相长度时,对动车组运行速度的影响,得出在设置分相时,为了减少速度损失,确保列车能顺利通过分相而不在分相内停车影响行车安全,应尽量将分相设置在坡度较小,入相速度大的位置。在设计分相时,也应尽量采用较短长度的分相。

本文侧重于从250 km/h动车组运行方面进行研究,分析了断电过分相对动车组运行的影响,然而分相位置的设计,需要考虑的因素较多,其设置位置和方式需要兼顾供电系统能力、动车组的运用方式、信号布点、线路纵坡、道岔布置、桥隧分布、接触网抢修等实际情况,进行优化设计、检算和系统联调测试；此外,在实践中电分相一般是上下行方向并置,在设置电分相时需结合上下行考虑。因此本文所得出的研究成果目前还有一定的局限性,需在今后的工作中做进一步研究。

[1] 高自友,李克平,李峰.固定闭塞条件下列车运行模拟控制方法：中国20071011-9225[P].2007-12-19.

[2] Li K P,et al. Cellular automaton model for railway traffic[J]. Journal of Computational Physics,2005,209:179-192.

[3] Li K P,et al. Modeling the railway traffic using cellular automata model[J]. International Journal o-f Modern Physics C,2005,16：921-932．

[4] K. Nagel and M. Schreckenberg. A cellular automaton model for freeway traffic[J]. J. Phys. I France,1992(2)：2221-2229.

[5] Ning B,et al. Modeling fixed-block railway signaling system using cellular automata model[J]. Intern-ational Journal of Modern Physics C,2005,16:1793-1801.

[6] 周华亮,等.准移动闭塞系统的元胞自动机模型及列车延迟传播规律的研究[J].物理学报,2006，55(4)：1706-1710.

[7] 李峰,等.固定闭塞系统中列车流的特性分析[J].物理学报,2007,56(6)：3158-3165.

[8] 钱勇生,等.考虑公交港湾式停靠的多速混合城市交通流元胞自动机模型研究[J].物理学报,2008，57(4)：2115-2121．

[9] 汪海龙,钱勇生.基于元胞自动机理论的客运专线通过能力模拟[J].铁道运输与经济,2008(7):82-84.

[10] Qian Yongsheng,Shi Peiji,Zeng Qiong,et al. A study on the effects of the transit parking time on traffic flow based on cellular automata theory[J]. Chinese Physics B,2010,19(4):5044-5049．