断裂分段之间不同相互作用对断裂运动的影响
2012-01-08白玉柱徐锡伟
白玉柱,徐锡伟,徐 杰
(中国地震局地质研究所,北京 100029)
断裂分段之间不同相互作用对断裂运动的影响
白玉柱,徐锡伟,徐 杰
(中国地震局地质研究所,北京 100029)
采用速度和状态摩擦本构控制的一维弹簧滑块模型研究断裂分段间相互作用对运动特征的影响,为研究东昆仑活动断裂带库赛湖段和西大滩段2个断裂分段之间的相互影响,采用由弹簧相连的2个滑块模拟断裂分段,通过弹簧滑块系统的动力学分析,将断裂运动性质的描述归结为一组微分方程,数值求解该微分方程组,最终得到断裂运动性质的参数,从而达到确定断裂未来强震复发周期的目的。通过位错模型计算、借鉴前人研究成果以及古地震资料确定模型相关参数。研究断裂分段在不同相互作用下的强震复发周期,模拟表明断裂间不同相互作用对地震复发周期和地震时断裂错动位移的大小没有规律性的影响;只是对地震发生时断裂错动的速度有明显的影响,作用强时,地震发生时断裂错动速度大;反之,地震发生时断裂错动速度小。
断裂;弹簧滑块模型;强震复发周期
0 引言
众所周知,多数地震的产生源于活动断裂的错裂运动。若能详细描述断裂错裂运动的历史,则对未来发生于该断裂上的地震会有系统认识。描述断裂运动的力学模型目前主要有动态断裂模型、动态位错模型等,这些模型在时间尺度上有所限制,只能描述地震发生时几十至几百秒内的断裂错动;描述断裂在地质史上的运动略显不足。活动断裂在地质史上的运动表现为粘着-滑动两种形式,粘着对应平静期,滑动对应地震活动期,且滑动运动在整个断裂运动历史中占据非常小的部分。因此对断裂运动的精确描述应当包含粘着和滑动2种运动。目前,许多研究表明弹簧滑块模型(或B K模型)在描述断裂粘着-滑动运动方面有较强优势。
弹簧滑块模型作为一个地震预测模型于上世纪七十年代由Buridge和Knopoff[1]提出。随后,该模型得到很大发展[2-7]。最初B K模型采用速度依赖型摩擦本构。事实上,更加接近地球物理性质的为速度和状态依赖摩擦本构关系,该本构关系是Dieterich[8-10]和 Ruina[11-12]在进行岩石摩擦滑动实验研究中得到的。该定律指出剪应力依赖于法向正应力、滑移速度和表征滑移历史的状态变量,该定律在模拟多变的震源破裂过程,如震前滑移、震后滑移、同震滑移、蠕变和地震轮回等现象时优越性突出。将速度和状态依赖摩擦本构关系应用到B K模型中是B K模型的发展方向之一,关于该方面的研究,目前理论上较完善,Rice和Tse[13]研究了单自由度弹簧滑块系统非线性运动的完整性,并模拟了走滑断裂上的地震轮回;Cao和Aki[14]采用该定律控制下的一维弹簧质点模型研究了地震;Jeen Hwa Wang[15]解析研究了速度和状态依赖摩擦本构控制的弹簧滑块模型的运动稳定性。国内这方面研究主要有:张继峰[16]考察了两自由度B K模型的摩擦激振问题。王威[17]基于速度和状态依赖摩擦定律的单自由度弹簧滑块模型,重点研究了滑动速率及系统刚度对断裂滑动性质、系统演化过程的影响。
东昆仑活动断裂是青藏高原北部大型左旋走滑断裂,倾角大,运动形式主要为左旋,该断裂将东昆仑构造带分成许多条块,各条块之间既有区别又有联系[18]。因此便于采用一维弹簧滑块模型来模拟各断裂分段的运动以及分段之间相互影响。目前关于该地区古地震研究较多[19-28],这为进行数值模拟提供了重要依据,但古地震研究只能给出强震发生的时间,并不能预测断裂未来强震发生时错动位移的变化。本文采用速度和状态摩擦本构控制的一维B K模型模拟东昆仑活动断裂带西部库赛湖段与西大滩段之间相互作用对强震复发周期的影响。在库赛湖断裂和西大滩断裂分段之间不同相互作用下,给出断裂滑动位移和速度随时间的变化,从而评价地震活动性。
1 地质构造背景
东昆仑断裂带西起青海新疆交界鲸鱼湖以西,向东经库赛湖、西大滩、东大滩、阿拉克湖和玛沁,东至甘肃省玛曲以东,绵延约1600km[19-20],构造上分6段。库赛湖段断裂西起布喀达板峰,沿昆仑山南麓N80°W方向延伸,经库赛湖北缘、昆仑山口北。东止于卡玛尼尔多湖附近,全长350~400km[29]。西大滩段断裂沿西大滩-东大滩谷地近东西向展布,西起大红石沟,向东经巴拉大才曲沟头、惊仙谷口、西大滩、东大滩和西藏大沟,东达秀沟盆地南侧,全长约250km[19-20]。西大滩段的断裂迹线与其南部1~2km的库赛湖断裂汇而不交,成为这两个分段的自然分段边界[29]。位置如图1所示。
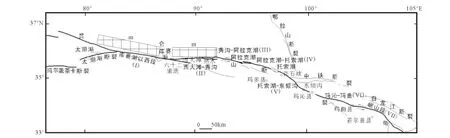
图1 库赛湖断裂和西大滩断裂位置图
有关东昆仑古地震复发间隔的周期,不同学者有不同观点,并且差别比较大。如,胡道功[19]通过古地震探槽和断裂地貌填图认为晚第四纪以来库赛湖段断裂地震活动性具有准周期性,其平均重复间隔为3000多年;刘光勋[22]基于东昆仑构造背景演化的角度计算出东昆仑活动断裂带大震强烈活动的平均时间间隔为2000a,实际上各个断裂分段的强震复发周期应当是不同的;但是Aiming Lin[23]认为库赛湖断裂在过去的7100a中地震复发周期为320~410a,许洪泰[24]认为是307~458a,李海兵[25]认为是250~350a。因此这里取库赛湖断裂的地震复发间隔为250~400a;西大滩段断裂自晚第四纪以来的强震活动周期平均为4000多年[20],Jianming Guo[26]认为西大滩的地震复发周期为1200a,Van der Woerd[27]采用最新的宇宙射线测年法得到西大滩的地震复发间隔为1200a;而吴珍汉[28]得到的西大滩地震复发周期为900~1700a,这里认为西大滩地震复发间隔的合理周期应当是900~2000a。关于该地区的历史地震资料非常有限,因此由理论计算预测未来强震发生时断裂的滑动位移十分必要。
2 弹簧滑块模型
将两段断裂简化为由弹簧相连的滑块1和滑块2,同时每个滑块分别通过弹簧和固定面相连,滑块1对应库赛湖断裂,滑块2对应西大滩断裂,如图1、图2所示。
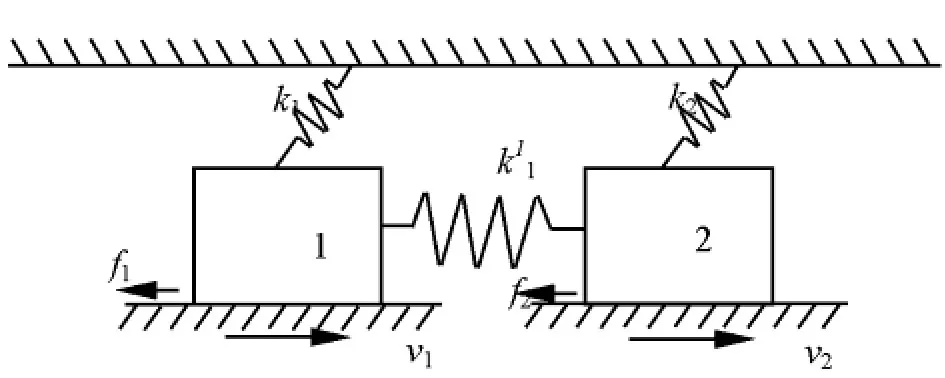
图2 库赛湖断裂和西大滩断裂模型示意图
滑块1和2的动力学方程为:
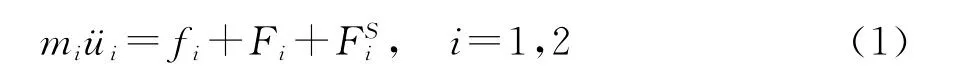
其中mi为滑块质量,ui为滑块相对平衡位置的位移,fi为滑块与运动支撑面之间摩擦力,Fi为滑块与固定面之间弹簧的恢复力,FSi为连接两滑块的弹簧恢复力。Fi和FSi的形式为:

其中μi(i=1,2)为滑块与运动支撑间接触面的摩擦系数;fni为滑块对运动支撑施加的法向作用力;kl1为连接两滑块弹簧的刚度;ki为滑块与固定面之间弹簧的刚度;由速度和状态依赖摩擦本构关系[8-12]。
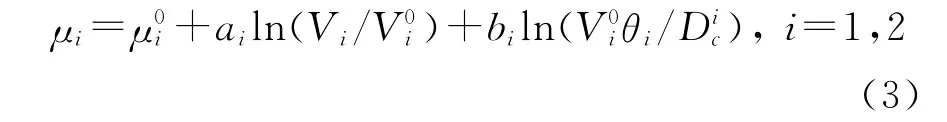
式中:μ0i为滑块以参考速度V0i做稳态滑动时接触面上的摩擦系数;Dic为滑块与运动支撑接触界面的特征长度;θi为滑块的状态变量;Vi为滑块相对支撑底面的滑动速度;ai和bi为常数,状态变量θi随时间的变化为:

式中:Vbi为支撑面的运动速度。数值求解方程(1)、(4)、(5)和(6),最终得到描述滑块(断裂)运动物理量。
模型中滑块参数这样确定:弹簧刚度ki由断裂位错模型[30-31]计算;由前人研究资料确定参数ai和bi;法向作用力Fni和滑块质量mi由断裂几何形状、延伸深度[26]和岩石平均密度计算求得;断裂几何参数参考现有成果[19-21,29],最终模型参数如表1所示。具体参数的确定参见附录。
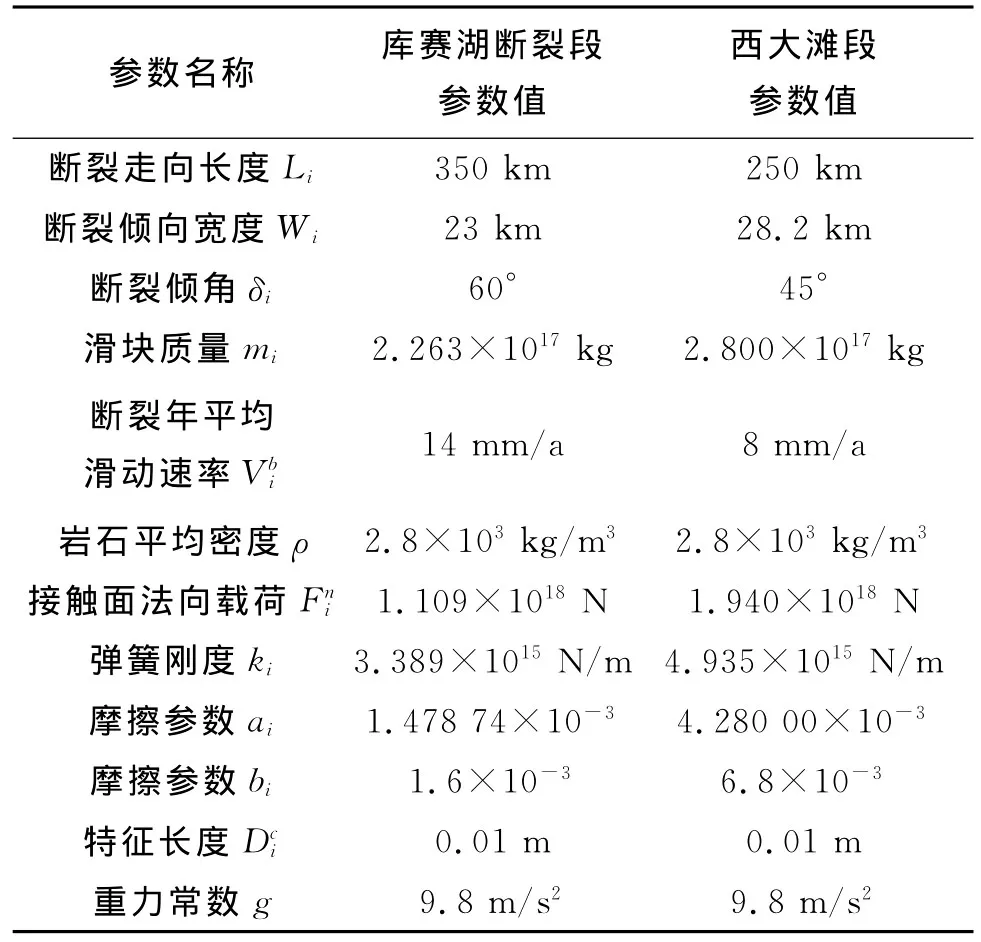
表1 模型参数
3 计算结果与讨论
(1)断裂分段滑动位移随时间的变化
图3和图4分别是断裂分段间不同相互作用下的滑动位移随时间的变化情况,图中用不同线型表示了不同kl1值下,库赛湖断裂和西大滩断裂滑动位移随时间的变化。其中图3关于库赛湖断裂模拟了5000a,约15个强震周期;图4关于西大滩断裂模拟了6000a,约3个强震周期。
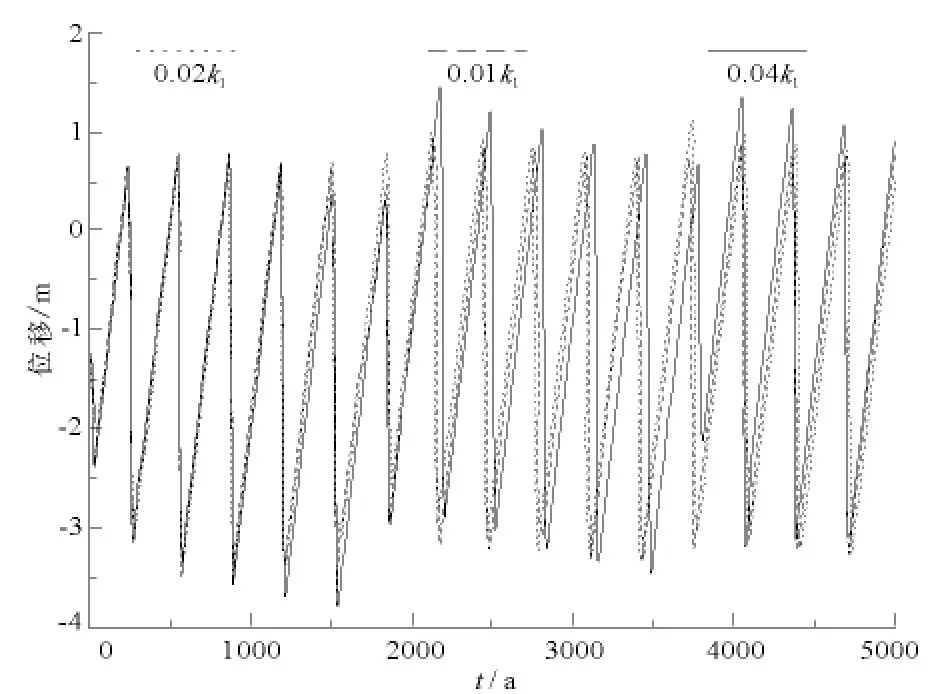
图3 不同相互作用下库赛湖断裂滑动位移随时间的变化
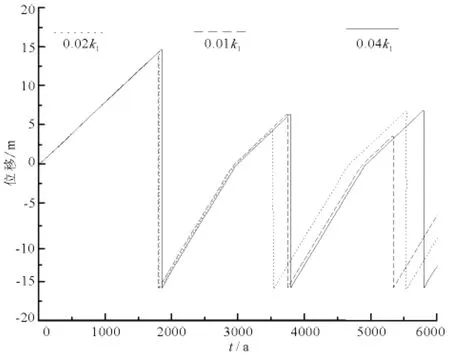
图4 不同相互作用下西大滩断裂滑动位移随时间的变化
由图3和图4可知,在不同相互作用下,断裂分段的地震复发周期差别不大;库塞湖断裂的地震复发周期差别很小,尤其是在前5个周期内根本没有差别,平均地震复发周期约为300a;西大滩断裂也是在第2个周期以后才有明显的差别,平均地震复发周期为1800a。但作用较强还是较弱,对断裂分段地震复发周期没有规律性的影响,比如西大滩断裂在=0.01k1下的周期比=0.04k1时小。此外,断裂间不同相互作用对强震复发周期的影响在经历较长的时间后才会有所体现,如库赛湖断裂分段在前5个周期之后,即1500a之后;西大滩断裂在1个周期之后,即1800a之后。
比较图3和图4可知,每次强震时,西大滩断裂错动的位移比库赛湖断裂要大,造成这种情况的原因可能是相比于库赛湖断裂而言,西大滩断裂的质量很大,且对应弹性系数k2较大,因此在库赛湖断裂与西大滩断裂组成的系统中,西大滩断裂的运动特征起到控制整个系统运动的作用。
(2)断裂分段滑动速度随时间的变化
图5和图6分别是断裂分段间不同相互作用下的滑动速度随时间的变化情况,图中用不同线型表示了不同值下,库赛湖断裂和西大滩断裂滑动速度随时间的变化。
与图3和图4类似,由图5和图6可发现,在较短时间内,如库赛湖断裂前5个发震周期和西大滩前1个地震复发周期之后,断裂间不同相互作用对断裂滑动速度的影响才体现出差异。与情况(1)不同,断裂间强相互作用使得地震发生时断裂错动的速度快;相互作用较弱时,使得地震发生时断裂错动速度较小。比较图5和图6可知,发生地震时西大滩断裂的错动速度小于库赛湖断裂的滑动速度。
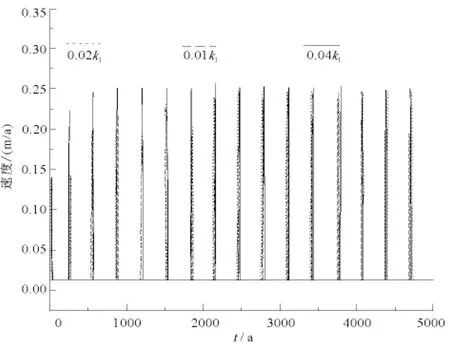
图5 不同相互作用下库赛湖断裂滑动速度随时间的变化
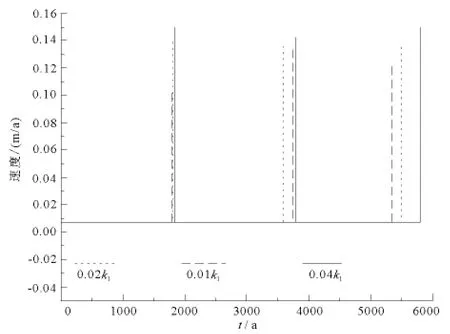
图6 不同相互作用下西大滩断裂滑动速度随时间的变化
4 结论
由西大滩和库赛湖断裂之间相互影响的研究得到如下结论:
(1)与现有古地震研究成果一致,数值模拟表明西大滩和库赛湖断裂都有各自单独破裂或共同破裂形成强震的可能;
(2)将模拟结果与现有古地震资料对比,作者认为在不考虑东昆仑断裂带其它断裂段(如秀沟-阿拉克湖断裂、阿拉克湖-托索湖断裂等)的影响下,目前西大滩与库赛湖断裂段之间的相互作用为上述几种情况中的任意一个都是合理的;
(3)不同相互作用下,库赛湖断裂段和西大滩断裂段发生地震震级可能不同,这是因为2段断裂强震发生时左旋错动的幅值和速度均不同;
(4)断裂间不同相互作用对各自强震复发周期及地震时错动位移没有规律性的影响;但相互作用强时使地震发生时断裂错动的速度加大。
附 录
断裂的几何参数,如断裂走向长度、断裂倾角以及断裂年滑动速度都取自现有的研究成果。其他参数的具体确定如下:
一、滑块质量的确定
计算模型参数需要通过断裂的参数来确定,用到的断裂参数主要有:mi为断裂上盘的质量;ki为弹簧刚度为断裂面上作用的法向载荷;Vb为断裂下盘相对上盘的运动速度;a,b,Dc分别为速度和状态摩擦本构关系中的常数和特征距离。
如图A所示,Li为断裂走向长度;Wi为断裂倾向长度;δi为断裂倾角。其中一些参数通过假设获得,因为板内大地震的震源深度主要集中在地下10~30km,因此在图A中令d1=10km,d2=3km。岩石平均密度设为ρ=2.8×103kg/m3。重力常数定为g=9.8m/s2。滑块的质量对应于断裂上盘体积Vol的质量。前面已经假设了d1和d2的值。令Y=(d2-d1)/tanδ,所以上盘的体积为Vol=((d1+d2)/2)YL=4.0×108L/tanδ,因此滑块对应的质量为:
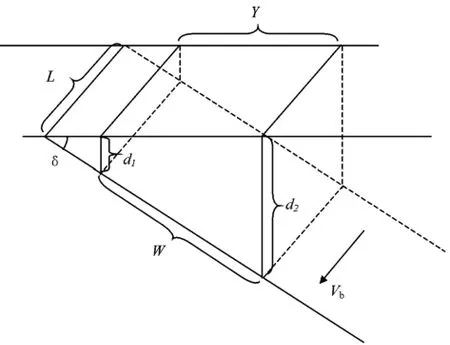
图A 断裂参数计算示意图
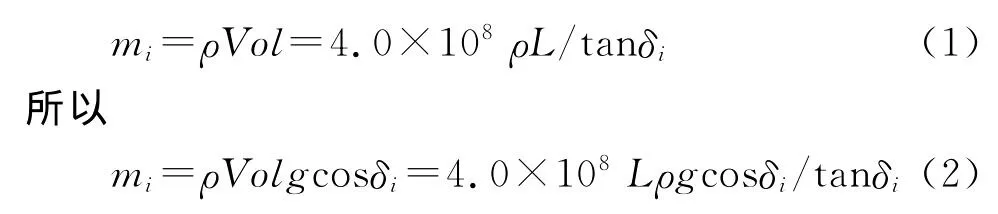
按照公式(2)可计算出两滑块的质量。
二、滑块与固定支撑间弹簧刚度的确定
因断裂面假设为矩形。在滑块粘着状态时,由于地面运动对滑块施加的载荷等于矩形断裂面滑动单位距离应力的增加值与相对滑移距离及断裂面积的乘积,即:
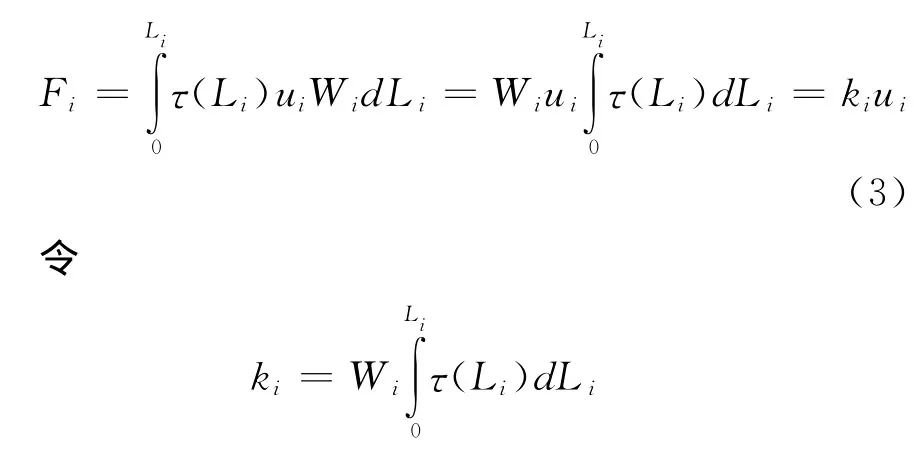
其中τ(Li)可以使用均匀半空间中的位错模型计算。τ(Li)计算出来后,在断裂长度方向上取和可得积分项的值。弹性位错模型参考文献[29-30]。
三、滑块与运动支撑接触面上法向应力的确定
滑块与运动支撑接触面上的法向应力对应于断裂上盘作用与断裂面上的法向应力,其大小如图所示为断裂上盘体积Vol的块体的重力在断裂面法向上的分量,大小由下式确定:
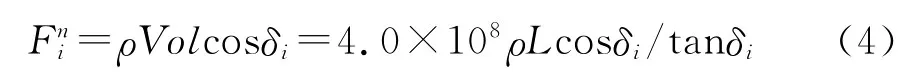
四、摩擦参数的确定
摩擦参数a,b和断裂面特征滑移距离Dc通过结合现有的研究成果却行。a,b和Dc根据Dieterich[8-10]的文献来取。
[1] Burridge,R,Knopoff,L.Model and theoretical seismicity[J].Bull Seismol Soc Am.,1967,57:341-371.
[2] Carlson,J.M and Langer,J.S.Properties of earthquakes generated by fault dynamics[J].Phys Rev Lett.,1989a,62:2632.
[3] Carlson,J.M and Langer,J.S.Mechanical model of an earthquake fault[J].Phys Rev A.,1989b,40:6740-6484.
[4] Carlson,J.M.Time intervals between characteristic earthquakes and correlations with smaller events:An analysis based on a mechanical model of a fault[J].J.Geophys Res.,1991a,96(3):4255-4267.
[5] Carlson,J.M.Two-dimensional model of a fault[J].Phys Rev A.,1991b,44:6226-6262.
[6] Carlson,J.M,Langer,J.S,Shaw,B.E and Tang,C,Intrinsic properties of a Burridge-Knopoff model of an earthquake fault[J].Phys Rev A.,1991c,44:884-897.
[7] Carlson,J.M,Langer,J.S and Shaw,B.E,Dynamics of earthquake faults[J].Rev Mod Phys.,1994,66:657-670.
[8] Dieterich,J.H.Time-dependent friction and mechanics of stick-slip[J].Pure Appl Geophys,1978,116:790-806.
[9] Dieterich,J.H.Modeling of rock friction,1,Experimental results and constitutive equations[J].J.Geophys.Res.,1979a,84:2161-2168.
[10] Dieterich,J.H.Modeling of rock friction,2,Simulation of preseismic slip[J].J.Geophys.Res.,1979b,84:2169-2175.
[11] Ruina,A.L.Friction laws and instabilities:A quasi-static analysis of some dry friction behavior[D].Ph.D.thesis,Brown Univ.Providence,R.I.1980.
[12] Ruina,A.L.Slip instability and state variable friction laws[J].J.Geophys.Res.,1983,88:359-370.
[13] Rice,J.R and Tse,S T.Dynamic motion of a single degree of freedom system following a rate and state dependent friction law[J].J.Geophys.Res.,1986,91:521-530.
[14] Cao,T and Aki,K.Seismicity simulation rate-and state-dependent friction[J].Pure Appl Geophys,1986,124:487-513.
[15] Wang Jeen-Hwa.A dynamic study of two one-state-variable,rate-dependent and state-dependent friction laws[J].Bull Seism Soc Am.,2002,92(2):687-694.
[16] 张继峰,冯奇.两自由度的Burridge-Knopoff模型的一种近似分析方法[J].力学季刊,2008,29:66-71.
[17] 王威,任青文,杜小凯,等.滑动速率及系统刚度对断层滑动性质影响研究[J].南京理工大学学报(自然科学版).2007,31(6):784-788.
[18] 范丽琨,蔡岩萍,梁海川,等.东昆仑地质构造及地球动力学演化特征[J].地质调查与研究,2009,33(3):181-186.
[19] 胡道功,吴中海,吴珍汉,等.东昆仑断裂带库赛湖段晚第四纪古地震研究[J].第四纪研究,2007,27(1):27-34.
[20] 胡道功,叶培盛,吴芳,等.东昆仑断裂带西大滩段晚第四纪古地震研究[J].第四纪研究,2008,28(2):214-221.
[21] 青海省地震局,中国地震局地壳应力研究所.东昆仑活动断裂带[M].北京:地震出版社,1999.
[22] 刘光勋.东昆仑活动断裂带及其强震活动性[J].中国地震,1996,12(2):119-126.
[23] Aiming Lin,Jianming Guo,Ken-ichi Kano.et al.2006.Average slip rate and recurrence interval of large-magnitude earthquakes on the Western Segment of the Strike-slip Kunlun Fault,Northern Tibet[J].Bull Seism Soc Am.,96(5):1597-1611.
[24] 许洪泰,闵伟.利用地震矩和实时概率模型对中长期地震危险性进行评价-以东昆仑和阿尔金断裂为例[J].地震研究,2007,30(2):120-126.
[25] 李海兵,司家亮,潘家伟,等.活动断裂的变形特征及其大地震复发周期的估算[J].地质通报,2008,27(12):1968-1991.
[26] Jianming Guo,Aiming Lin,Tadashi Maruyama.et al.New constrains on recent large earthquakes along the Xidatan-Dongdatan Segment of the Kunlun Fault,Westren China[J].Bull Seism Soc Am.,2006,96(1):48-58.
[27] Van der Woerd J,Ryerson F J,Tapponnier P.et al.Holocene left-slip rate determined by cosmogenic surface dating on the Xidatan Segment of the Kunlun fault(Qinghai,China)[J].Geology,1998,26(8):695-698.
[28] 吴珍汉,胡道功,吴中海,等.东昆仑南部西大滩断裂的地震鼓包及形成时代[J].地质评论,2006,52(1):15-25.
[29] 徐锡伟,陈文彬,于贵华,等.2001年11月14日昆仑山库赛湖地震(MS8.1)地表破裂带的基本特征[J].地震地质,2002,24(1):1-13.
[30] Okada.Y.Surface Deformation due to shear and tensile faults in a half-space[J].Bul1Seis Soc Am.,1985,75:1018-1040.
[31] Okada.Y.Internal deformation due to shear and tensile faults in a half-space[J].Bull Seis Soc Am.,1992,82:1018-1040.
[32] 陶玮,沈正康,万永革,等.根据2001年Mw7.8可可西里强震InSAR同震测量结果反演东昆仑断裂两侧地壳弹性介质差异[J].地球物理学报,2007,50(3):744-751.
[33] 何昌荣.速度与状态依赖性摩擦本构关系下双滑块系统的相互作用[J].中国科学:D辑,2003,33:53-59.
The Effect of Different Interaction between Fault Segments on Their Sliding Motion
BAI Yu-zhu,XU Xi-wei,XU Jie
(Institute of Geology,CEA,Beijing 100029,China)
In this paper,we apply the spring-block model controlled by the velocity and state depended frictional constitutive relation to research the effect of interaction between two fault segments on their motions.In order to research the effect of interaction between Kusai Lake and Xidatan segment of East Kunlun fault,we use two blocks connected by spring to simulate these two fault segments.Through the dynamical analysis,we get the differential equations to depict fault segment motion.Numerically solving the fault motion equations,we have the parameters of fault motion and determine the recurrence of strong earthquake.With the help of dislocation model research achievements of previous scholar and the data of paleo-earthquakes,we determine the related parameters of spring block model.Through the simulation,we find that the interaction between Kusai Lake and Xidatan fault segment has no regularity effect on recurrent period of earthquake and sliding displacement when earthquake happen,but the strong interaction will make the quick slip velocity of fault and the weak interaction will make the slow one.
fault;spring-block model;strong earthquake recurrent period
P315.2
A
1003-1375(2012)02-0033-06
2011-04-13
中国地震局地质研究所基本科研业务专项(IGCEA0912)
白玉柱(1976-),男(汉族),河北邯郸人,助理研究员,主要从事强地震动研究.E-mail:yuzhubai 2008@126.com.
