对“地震条件下挡土墙主动土压力及 其分布的统一解”的讨论
2012-01-08林宇亮
林宇亮
(中南大学 土木工程学院,长沙 410075)
笔者拜读了发表在《岩土力学》2012 年第33卷第1 期上的“地震条件下挡土墙主动土压力及其分布的统一解”一文[1](以下简称原文)。笔者对原文有几处疑问,望能得到释疑和解答。
式(1)中的最后两项是不能忽略的,尤其是在水平加速度系数hk 较大时。而原文并没有对基本平衡方程式(4)~(6)进行求解。
(2)原文在对水平地震加速度系数hk 进行隐含处理时,得到了隐含处理转换方程式(8)~(11)。从原文中式(8)~(11)可以看出,pτ′、np′、Rτ′和nR′应分别是微分单元edgf 相应截面上的切向和法向合力,当采用原文中式(12)来计算p′时,p′指的是pτ′和np′的合力。另一方面,原文在求解地震土压力时应用了王渭漳等[2]的部分公式,得到了地震土压力计算式(16),而式(16)得到的p′的表达式是土压力的分布强度,而非微分单元edgf 中ef 截面上的切向合力和法向合力np′的矢量和。同一篇文章中若采用p′表达两个物理概念是欠妥的。因此,笔者认为,式(8)~(11)应分别改写为
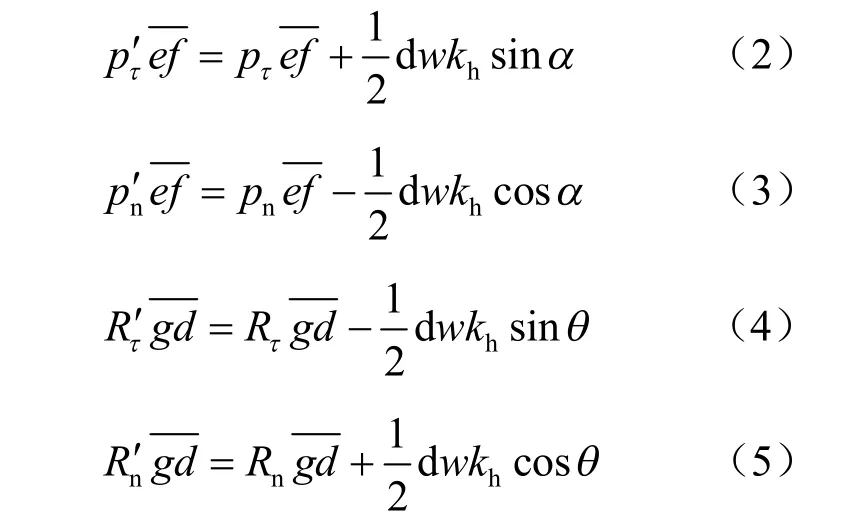
(3)原文在对水平地震加速度系数隐含处理转换后,得到了转换后的ef 边中点的作用力p′、gd边中点的作用力R′、土楔体AC 面受到的作用反力与AC 面法线夹角φ′、以及土楔体AB 面受到的作用反力与墙背面AB 法线夹角δ′的表达式,如原文式(12)~(15)所示。显然,p′、R′、φ′和δ′不仅是破裂角θ 的函数,也是墙背高程h 的函数。中间变量1n 、2n 、3n 、a、b、1m 、2m 、3m 等均也是墙背高程h 的函数。因此,原文式(26)通过对土压力分布强度沿墙高h 求积分的方法来求解土压力合力,从而得到土压力合力表达式(27)是有误的。因为原文中式(26)不仅p′是墙高h 的函数,中间变量1m 、2m 、3m 也是h 的函数,也应进行积分处理。同样,也无法得到土压力合力作用点位置的表达式
(30)。
而文献[2]的研究成果和原文是有区别的。文献[2]得到的土压力分布强度p 的表达式为

其中:

由此可见,由文献[2]得到的土压力分布强度p的表达式中1m 、2m 、3m 均是与墙高h 无关的中间量。因此,在求解土压力合力时,将土压力分布强度p 沿墙高h 进行积分时不需要再对1m 、2m 、3m进行积分处理。
(4)在进行破裂角和土压力合力计算时,原文采用图解法获得了土压力合力公式(47)和破裂角公式(49),并给出了考虑地震荷载时的中间变量1I 、2I和3I 的表达式(53)~(55)。结合原文公式可发现,只要求得φ′和δ′便能方便求解土压力合力和破裂角。原文提出采用迭代计算求解φ′和δ′,迭代计算应结合φ′和δ′的表达式(14)和(15),但φ′和δ′表达式中的变量h 将会使得迭代计算无法进行。
[1] 孙勇. 地震条件下挡土墙主动土压力及其分布的统一解[J]. 岩土力学, 2012, 33(1): 255-261. SUN Yong. Unified solution of seismic active earth pressure and its istribution on a retaining wall[J]. Rock and Soil Mechanics, 2012, 33(1): 255-261.
[2] 王渭漳, 吴亚中. 重力式挡土墙墙背土压力及其分布的研究[J]. 中南公路工程, 1992, (1): 22-29.
