基于含水劣化特性的隧道围岩时效变形数值计算
2012-01-08刘新荣
黄 明 ,刘新荣,邓 涛
(1. 福州大学 土木工程学院,福州 350108;2. 重庆大学 土木工程学院,重庆 400045)
1 引 言
许多岩体工程的失稳是由于岩石及结构面的时效变形积累而导致的流变破坏,而水是诱发各种工程地质灾害最活跃的载体。岩石的时效变形行为及流变破坏源于其内部损伤随时间的逐渐积累,且同时伴随着宏观主裂纹的流变时效扩展,而水是造成岩石这种损伤的一个重要原因[1]。因此,对于存在地下水作用的大坝基础、边坡和地下洞室等岩体工程而言,其长期稳定性不单纯取决于应力作用下岩石和结构面本身的流变行为,而是依赖于应力与水长期共同作用下的耦合流变过程。
目前针对岩体工程流变问题的研究已开展大量的工作,且因为实际岩体工程的计算需要,不少学者还借助商业软件的二次开发平台,尝试将自定义的本构模型嵌入到软件中进行计算。以大型通用软件FLAC 为例,Malan[2]提出了一个流变软化弹-黏塑性模型,并加入到FLAC 中用于分析南非某金矿矿井开挖后硬岩流变行为;Boidy 等[3]将Lemaitre黏塑性模型加入到FLAC 中,对瑞士的一个有蠕变行为的隧道围岩作了反分析;Dragan 等[4]提出一个反映铁矿岩石硬化软化行为的弹塑性模型和一个描述延迟体积膨胀的Lemaitre 黏塑性蠕变模型,并加入到FLAC 中,进行了巷道开挖问题短期和长期力学行为分析。国内学者[5-10]也进行过类似的研究,并获得了较多成果,但基于含水劣化的岩石流变特性及其相关问题研究,目前绝大部分仍停留在机制分析及模型的构建上,而对于模型的实际工程应用研究较少。本文将在模型研究的基础上,针对考虑含水劣化特性的岩石黏弹塑性模型进行FLAC3D程序二次开发,并应用于实际的隧道工程进行不同含水状态下围岩的稳定性计算和二次支护时机的预测,以求得到能够更好解决实际问题的研究成果。
2 岩石黏弹塑性模型有限差分格式
文献[11]提出了一个考虑塑性的改进Burgers模型,其中的M-C 元件,在应力σ 未达到Mohr- Coulomb 准则屈服应力sσ 前应变为0,当应力等于或大于sσ 时则服从Mohr-Coulomb 塑性流动规律。本文结合文献[12]中建立的KBurgers 流变模型与M-C 元件串联,形成能模拟黏弹塑性偏量特性和弹塑性体积行为的KBurgers-MC 模型,并假定黏弹和黏塑应变率分量变形协调,模型结构如图1 所示。KBurgers-MC 模型具有瞬时弹性变形、衰减蠕变、等速蠕变、含水劣化和塑性性质,可以描述不稳定蠕变。模型的本构方程描述如下:
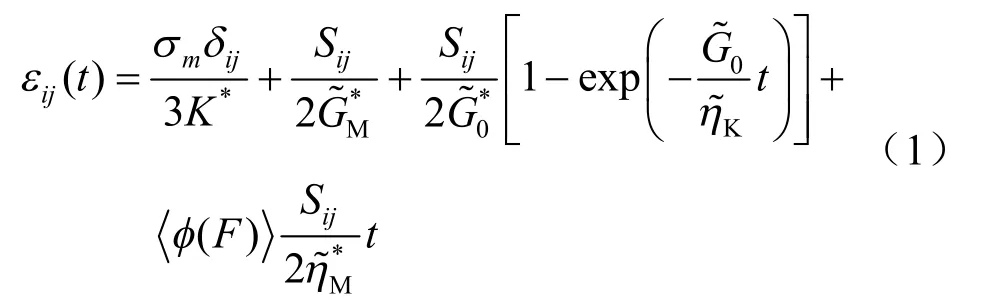
式中:δij为Kronecker 符号;σm= (σ1+ σ2+ σ3)/3;φ( F)为开关函数,当 F ≤ 0时, φ( F) = 0;当F > 0时, φ( F) = 1,其中,φ ( F)通常存在两种形式,φ ( F ) = ( F /)N或φ ( F) = eM(F/F0)- 1。基于此,结合泥质粉砂岩单轴蠕变试验结果[12]得到的开 关 函 数 表 达 式 为 F = σ1- σ3- 7.622 - 6.093⋅ exp(-0 .715 w),说明开关函数F 大小不仅与偏应力大小有关,而且与含水率的大小也有关,岩石含水率越大,则易使开关开启,即 F → 0+时的临界偏应力越小。K*= K ( w);=[1 -υ( w)];=⋅ [1 -υ ′( w)];=[1 -υ′( w)];[1-υ′( w)]。
总应变偏量速率:
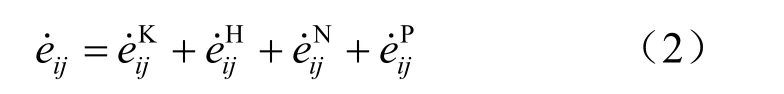
K 体:
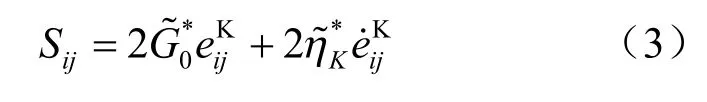
H 体:

修正N 体:

M-C 元件体:
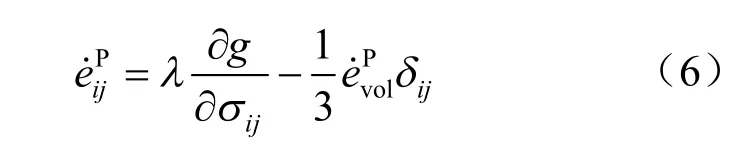
其中
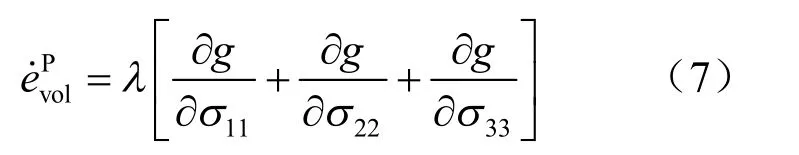
在塑性力学中一般假定球应力不产生塑性变形,因而整个模型的球应力速率可写为
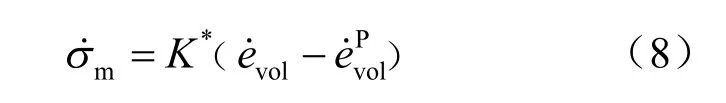

图1 KBurgers-MC 模型 Fig.1 KBurgers-MC model
对于应力超过屈服极限的情况,可由KBurgers- MC 模型来实现,此时模型中的M-C 元件对应岩石不同含水状态下基本力学参数黏聚力c、内摩擦角φ 和抗拉强度tσ 可通过室内常规试验获得。
为了采用FLAC3D进行二次开发,便于含水劣化蠕变模型程序化,通过有限差分进行推导可得
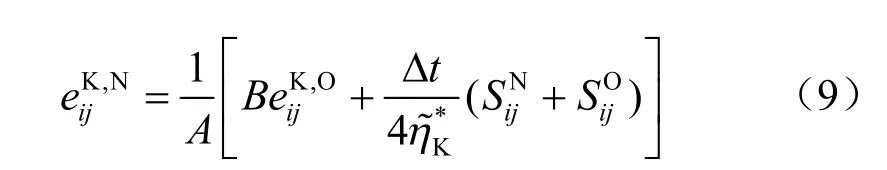
(1)当开关函数 0F ≤ 时
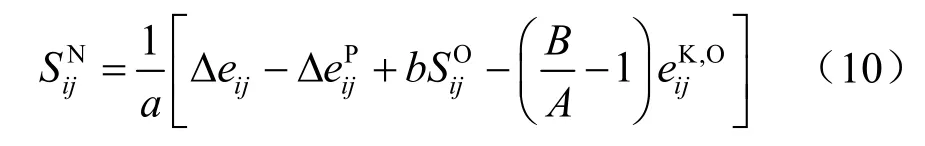
(2)当 0F> 时

球应力写成差分的形式为

类似式(10)、(11)的形式,可得到K 体新的球应变为

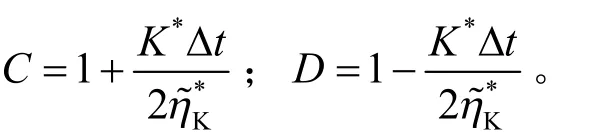
式中:
本文中的塑性流动法则采用的是不相关联的Mohr-Coulomb 流动法则,当屈服函数小于0 时,需要根据塑性应变增量来更新应力。此外,对于开关函数,在满足 0F ≤ 的情况下,此时除不考虑塑性应变外,修正N 体也不起作用。
以上分析表明,KBurgers-MC 模型的应力-应变关系可用式(10)~(12)进行表达。
3 黏弹塑性模型的程序实现与验证
对于KBurgers-MC 模型,在FLAC3D程序中的实现,相对于程序自带的Cvisc 模型,不同之处在于本文的模型存在带开关元件的修正N 体,且考虑了含水率变化对模型特性的影响。在程序编写过程中,对于参数含水劣化的描述可直接采用FLAC3D自带的FISH 语句实现,也可在程序内部实现,但模型开关状态应由开关函数 ( )Fφ 进行判别并在程序内部实现,本文以Cvisc 模型的源程序为二次开发蓝本,利用 C++语言编写获得[12]。采用Microsoft Visual C++6.0 对KBurgers-MC 模型进行程序化流程如图2 所示,得到的模型动态链接库文件为userkburgers.dll。以下将进行模型的有效性检验。
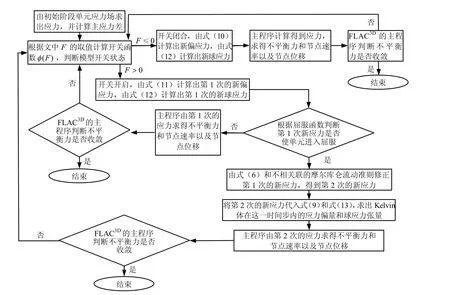
图2 userkburgers.dll 程序编写流程图 Fig.2 Preparation flowchart of userkburgers.dll program
(1)黏弹性特性。为了验证userkburgers 数值程序的正确性,基于一个单轴压缩的算例,对提出的岩石蠕变模型进行考证,模拟试件尺寸为高为 10 cm(Y 方向),直径为5 cm,共划分2 000 个单元,2 121 个节点,如图3 所示。模型底部在Y 方向约束,顶部施加分布压力10 MPa。采用本文的userkburgers 数值程序进行蠕变数值分析,以考证KBurgers-MC 模型的正确性。
首先对其黏弹性力学性质进行分析。Burgers模型中Maxwell 体的黏滞系数不进行赋值,则退化成广义Kelvin 模型。同样地,对于userkburgers 程序,对其中Maxwell 体的黏滞系数不赋值,且将黏聚力和抗拉强度赋一个很大的数值,就可保证计算过程中不会到达塑性状态,可针对性地讨论其黏弹性特性。对于模型算例计算参数,采用蠕变试验参数K= 2.959 5 GPa,0G=˜ 20.488 5 GPa,MG =˜ 1.400 3 GPa,Kη =˜ 20.845 4 GPa·h,含水率w = 0;对上端节点(0, 0, 0)不同蠕变时刻Y 方向(竖直方向)的位移进行计算。如图4 所示,两种模型计算的结果总体上一致,且基本上都在蠕变持续2 h左右达到稳定蠕变状态,这与实际试验结果较一致,采用两种蠕变模型数值计算得到的竖向位移最大值都在2.69 mε左右,表明本文编制的userkburgers 程序进行黏弹性分析具有可靠性。

图3 计算模型 Fig.3 Calculation model
(2)含水劣化特性。程序的含水劣化特性验证仍采用黏弹性验证的标准试件模型,模型的边界条件及材料参数均与前述一致,并令上端的加载应力σ=15 MPa,分别计算含水率w=0、1.5%、2.5%和3.74% 4 种情况下试件发生蠕变2 h 后的竖向位移,其最大竖向位移分别对应为0.516、0.598、0.629、0.647 mm,可见随着含水率的增大,试件顶部竖向位移越大,与室内试验结论相一致,说明userk- burgers 程序含水劣化特性的有效性。
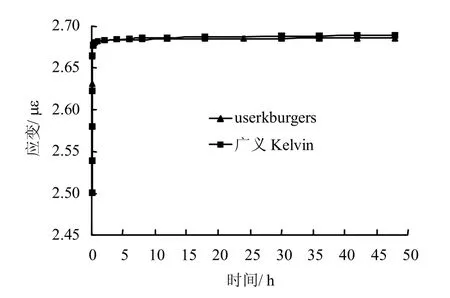
图4 两种模型单轴蠕变曲线 Fig.4 Uniaxial creep curves of two models with creep calculation for 48 hours
(3)塑性特性。进行塑性特性验证时,可与FLAC3D自带的Cvisc 模型对比,计算模型为1.0 m× 1.0 m×1.0 m 的立方体,中间开半径为0.2 m 的圆形孔洞,左、右边界加横向水平位移约束,前后边界加纵向水平位移约束,下底边加三向固定约束,上顶面施加面荷载20 MPa,计算参数在上文黏弹性参数基础上再加入Mη=˜ 1 367.521 4 GPa,c=11.0 MPa,φ=24.77°,计算过程中在圆形孔洞拱顶位置布设测点进行位移监测。蠕变计算为12 h 后,两种模型计算得到的塑性区开展范围基本相似,主要集中在孔洞周边一定厚度范围[12]。总体上,采用Cvisc 模型计算得到塑性区的开展范围要比采用userkburgers.dll 大,采用userkburgers.dll 计算得到的测点位移趋于稳定的时间要短,且拱顶最大沉降为8.174 mm,而采用Cvisc 模型得到的沉降值为8.89 mm,两者存在偏差说明userkburgers.dll 程序中开关元件在计算时起到有效作用。
4 工程应用
桃树垭隧道位于重庆市巫山县境内,为一座上、下行分离的4 车道高速公路长隧道。隧道左线长为1 267 m;右线长为1 202 m,最大埋深约为 183 m。施工期间曾经发生过大变形灾害,如图5所示。本文数值计算将选取隧道出口右线发生过大变形灾害的YK38+310~YK38+320 段。
4.1 模型建立及参数的确定
数值分析建立地质模型见图6,模型上边界取至地表,埋深约110 m,左、右侧和底部边界长度取隧道外缘50 m,模型基本参数以断面YK38+320 为准,纵向取10 m,围岩重度25 kN/m3,自然含水状态下黏弹性参数0G =˜ 3.243 3 GPa,Kη=˜ 3.299 8 GPa·h,MG =˜ 0.221 7 GPa,Mη =˜ 1 367.521 4 GPa·h,对于其他含水状态的黏弹性参数可分别进行瞬间弹性损伤和长期蠕变损伤考虑[12-13]。其他变形参数及强度参数如表1、2 所示。 模型的边界条件采用位移边界条件,顶部为自由变形边界,左、右边界施加水平约束,模型底面加固定支座约束,隧道纵向前后两个面施加Y 方向约束。主要对隧道台阶法开挖时周边测点的位移进行模拟计算,测点布置如图7 所示。

图5 隧道大变形灾害 Fig.5 Large deformation disaster of the tunnel
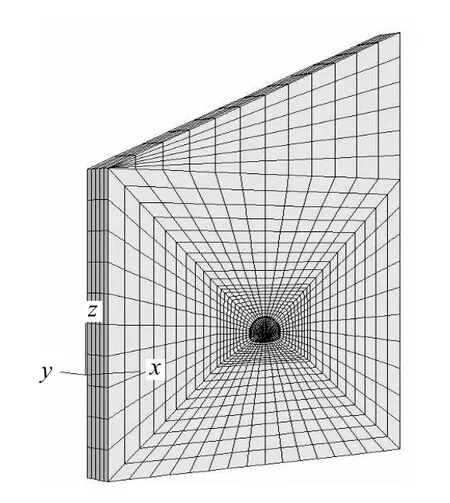
图6 计算模型 Fig.6 Calculation model

表1 岩体的力学参数 Table 1 Mechanical parameters of rock mass
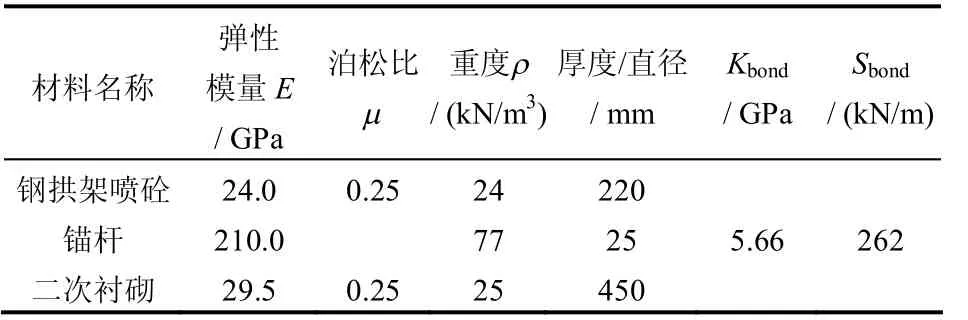
表2 支护材料力学参数 Table 2 Mechanical parameters of support materials
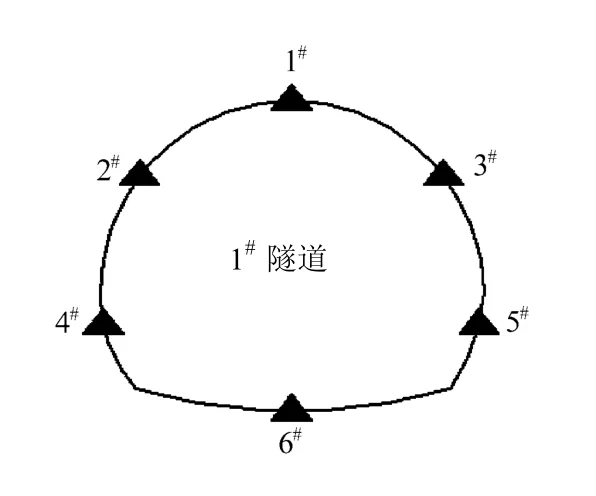
图7 测点及测线布置图 Fig.7 Layout of measuring points
4.2 结果分析
如图8、9 所示分别为自然含水状态和饱和状态下开挖并初期支护后60 d 内1#、2#和3#测点的变形计算结果。上台阶开挖后若停止开挖下台阶,则隧道变形将逐渐趋于稳定。6 d 后开挖下台阶,自然含水状态下隧道拱顶沉降45~50 d 后趋于稳定,水平收敛稳定需33~35 d,拱顶累积沉降为37.34 mm,水平收敛为16.95 mm。而饱和状态下,拱顶沉降和

图8 自然含水状态下开挖后60 d 内测点位移计算结果 Fig.8 Monitoring results of the upper measuring points in 60 days after bench excavation in the natural moisture state
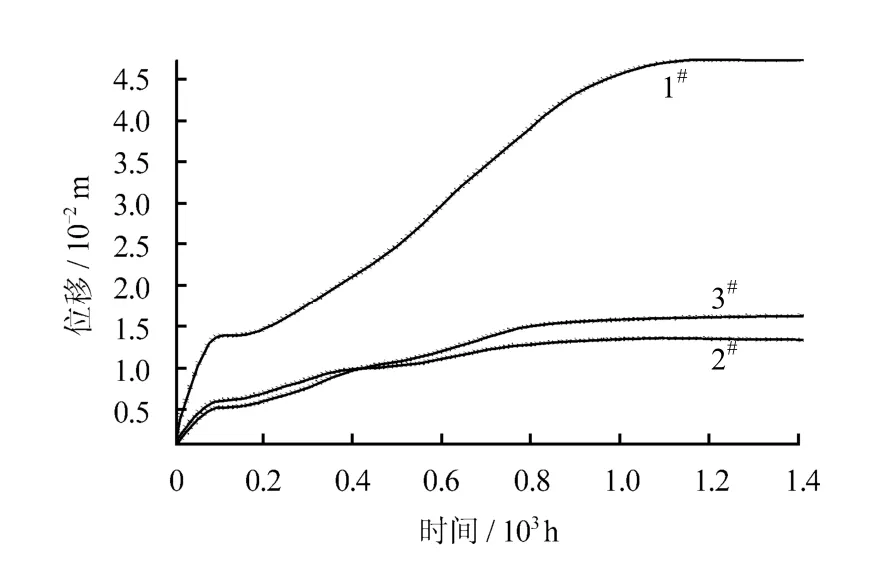
图9 饱和状态下开挖后60 d 内测点位移计算结果 Fig.9 Monitoring results of the upper measuring points in 60 days after bench excavation in the saturated state
水平收敛的稳定时间分别为47~50 d 和38~42 d,拱顶累积沉降为47.37 mm,水平收敛为29.94 mm。此外,下台阶开挖后隧道偏压现象较为明显,右拱腰(3#测点)位移明显比左拱腰(2#测点)大,且随着围岩含水率的增大偏压现象越明显,这与隧道现场监测结果相一致。
假设隧道开挖后不进行二次支护,则继续计算可得到如图10、11 所示结果,分别为自然含水及饱和状态下300 d 内测点的位移计算结果。由图可知,不进行二次支护则较长时间后拱顶沉降和水平收敛速率迅速增大,最终将导致隧道塌方或冒顶。自然含水状态下围岩自稳能力稍强,拱顶沉降和水平收敛进入加速变化阶段的时间约为开挖后120 d,由此可推测,二衬合理施作时间应为开挖后45~120 d内。饱和状态下围岩自稳能力相对较差,自稳时间要短,84 d 后将发生加速变形,可推测饱和状态下二衬合理施作时间为开挖后47~84 d。
开挖300 d 内不进行二次支护,则自然含水状态下隧道下断面水平收敛(4#与5#测点的相对位移)为41.47 mm,而饱和状态下达到了72.26 mm,说明地下水对隧道水平收敛影响效果显著。下断面水平收敛总体上比上断面大,自然含水状态下相差 7.4 mm,而饱和状态下相差23.94 mm。
开挖300 d 内不进行二次支护,自然含水状态下隧道底鼓变形(6#测点)随时间增长最终将趋于稳定,稳定时底鼓位移值达到44.6 mm;而饱和状态下,隧道开挖后44~105 d 内底板处于稳定状态,当未二次支护时间达到105 d 时底鼓变形将突然加剧,且变形速率越来越大,300 d 后底板底鼓值接近86.43 mm,约为自然含水状态下的2 倍,分析原因认为,地下水的长期作用使围岩的蠕变特性更为显著,含水率增大加剧了围岩变形,最终导致路基混凝土开裂、错台。

图10 自然含水状态下300 d 内测点的位移计算结果 Fig.10 Monitoring results of the measuring points in 300 days in natural moisture state
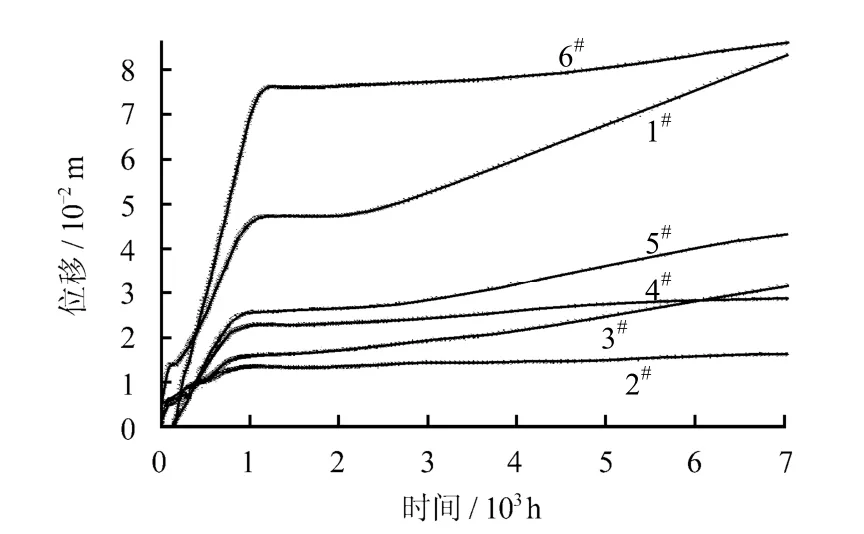
图11 饱和状态下测点300 d 内的计算结果 Fig.11 Monitoring results of the measuring points in 300 days in saturated state
饱和状态下若隧道开挖83.33 d 后进行二次衬砌施作,测点的位移计算结果如图12 所示。结果表明,拱顶沉降(1#测点)、水平收敛(2#~5#测点)及底鼓变形都趋于稳定。与之前无二次衬砌的计算结果比较,施作二次衬砌后围岩变形得到了有效控制,隧道整体趋于稳定。由此可见,二衬施作时机的确定是有效防止围岩大变形灾害发生的关键。

图12 饱和状态下合理施作二衬后的位移计算结果 Fig.12 Monitoring results of the measuring points in 300 days in saturated state after secondary lining
5 结 论
通过对可考虑含水劣化特性的岩石黏弹塑性模型的程序二次开发,得到了相应模型程序的动态链接库,并结合简单的算例对程序的有效性进行了检验,结果表明模型能较好地反映岩石的瞬时弹性变形、衰减蠕变、等速蠕变、含水劣化和塑性变形等特性。基于本文模型程序,通过对桃树垭隧道开挖过程中围岩稳定性进行模拟分析表明:
(1)饱和状态下拱顶累积沉降和水平收敛都比自然含水时大;下断面水平收敛总体上比上断面大,且围岩含水率越高这一现象越明显;围岩含水率越大,隧道偏压现象越显著。自然含水状态下隧道底鼓变形随时间增长最终趋于稳定,而饱和状态下隧道开挖一段时间内底板处于稳定状态,若长时间不进行二次支护则底鼓变形将突然加剧,最终将导致路基混凝土开裂、错台。
(2)通过对比300 d 内有、无二次支护下测点的变形情况表明,及时施作二衬可以较好抑制围岩变形的进一步发展,隧道整体将处于稳定状态。自然含水状态下合理施作时间应在开挖后45~120 d内,饱和状态下围岩自稳能力相对较差,二衬合理施作时间为开挖后47~84 d 内。
[1] SUN Jun, WANG Si-jing. Rock mechanizes and rock engineering in China: Developments and current state-of- the-art[J]. International Journal of Rock Mechanics and Mining Sciences, 2000, (37): 447-465.
[2] MALAN D F. Time-dependent behavior of deep level tabular excavations in hard rock[J]. Rock Mechanics and Rock Engineering, 1999, 32(2): 123-155.
[3] BOIDY E, BOUVAND A, PELLET F. Back analysis of time-dependent behavior of a test gallery in claystone[J]. Tunneling and Underground Space Technology, 2002, 17(4): 415-424.
[4] DRAGAN G, FRANCOISE H, DASHNOR H. A short-and long-term rheological model to understand the collapses of iron mines in Lorraine, France[J]. Computers and Geotechnics, 2003, 30(7): 557-570.
[5] 王贵君. 盐岩层中天然气存储洞室围岩长期变形特征.岩土工程学报, 2003, 25(4): 431-435. WANG Gui-jun. Long-term deformation characters of salt rock surrounding a gas storage cavern[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(4): 431-435.
[6] 徐平, 李云鹏, 丁秀丽, 等. FLAC3D黏弹性模型的二次开发及其应用.长江科学院院报, 2004, 21(2): 10-13. XU Ping, LI Yun-peng, DING Xiu-li, et al. Secondary development and application of visco-elastic constitutive model in FLAC3Dsoftware[J]. Journal of Yangtze River Scientific Research Institute, 2004, 21(2): 10-13.
[7] 褚卫江, 徐卫亚, 杨圣奇, 等. 基于FLAC3D的岩石黏弹塑性流变模型二次开发研究[J]. 岩土力学, 2006, 27(11): 2005-2010. CHU Wei-jiang, XU Wei-ya, YANG Sheng-qi, et al. Secondary development of a viscoelasto-plastic rheolo- gical constitutive model of rock based on FLAC3D[J]. Rock and Soil Mechanics, 2006, 27(11): 2005-2010.
[8] 徐卫亚, 杨圣奇, 褚卫江. 岩石非线性黏弹塑性流变模型(河海模型)及其应用[J]. 岩石力学与工程学报, 2006, 25(3): 433-447. XU Wei-ya, YANG Sheng-qi, CHU Wei-jiang. Nonlinear viscoelasto-plastic rheological model (Hohai model) of rock and its engineering application[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(3): 433-447.
[9] 刘建华. 岩体力学行为拉格朗日分析方法研究与工程应用[D]. 济南: 山东大学, 2006.
[10] 张强勇, 杨文东, 张建国, 等. 变参数蠕变损伤本构模型及其工程应用[J]. 岩石力学与工程学报, 2009, 28(4): 732-739. ZHANG Qiang-yong, YANG Wen-dong, ZHANG Jian- guo, et al. Variable parameters-based creep damage constitutive model and its engineering application[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(4): 732-739.
[11] 袁海平, 曹平, 许万忠, 等. 岩体黏弹塑性本构关系及改进Burgers 蠕变模型[J]. 岩土工程学报, 2006, 28(6): 796-799. YUAN Hai-ping, CAO Ping, XU Wan-zhong, et al. Visco-elastic-plastic constitutive relationship of rock and modified Burgers creep model[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 796-799.
[12] 黄明. 含水泥质粉砂岩蠕变特性及其在软岩隧道稳定性分析中的应用研究[D]. 重庆: 重庆大学, 2010.
[13] 黄明, 张旭东. 含水状态下T2b2泥质粉砂岩蠕变特性试验研究[J]. 工业建筑, 2011, 41(4): 77-81. HUANG Ming, ZHANG Xu-dong. Test study on the creep properties of T2b2siltite in different moisture states[J]. Industrial Construction, 2011, 41(1): 77-81.
