倒T 型导管墙桩基防波堤稳定性简化计算方法

王元战，张连丽，商 丹，肖 忠

（天津大学 天津市港口与海岸工程重点实验室，天津 300072）

1 引 言

随着港口工程建设规模的扩大，防波堤工程建设所处的水文地质条件更为恶劣，传统防波堤结构型式已不能满足工程需要。倒T 型导管墙桩基防波堤是一种适用于软土地基的新型防波堤结构，由T型截面的钢筋混凝土预制构件在海上连接组成。钢筋混凝土构件由底板、立板和肋板相互连接形成整体，在立板与肋板的交接线处设置竖向导管，钢桩或钢筋混凝土桩穿过竖向导管打入地基中形成桩基础，如图1 所示。桩与导管间存在缝隙以混凝土进行灌浆，从而使二者连成整体。倒T 型导管墙桩基防波堤具有重量轻、工作性能可靠、适用于软土地基、施工简便、工程造价较低等优越性，但对该结构底板与桩基联合承载特性、构件内力特性和失稳破坏模式等，还缺乏深入了解，尚未建立可靠的设计计算方法。

稳定性是海岸工程结构设计的最重要内容。文献[1－2]采用有限元方法研究了桶形基础平台结构的稳定特性；文献[3]建立了筒型基础防波堤稳定性分析的有限元方法，并研究了筒型基础防波堤结构的稳定特性；文献[4]在有限元分析的基础上，建立了筒型基础防波堤稳定性分析的简化计算方法。关于倒T 型导管墙桩基防波堤的稳定特性及其分析方法，尚无公开发表的文献资料。

本文在有限元模型分析的基础上，研究了倒T型导管墙桩基防波堤的失稳破坏特性，建立了倒T型导管墙桩基防波堤稳定性分析的简化计算方法，与有限元计算结果的比较表明，文中建立的简化计算方法是有效、可靠的。

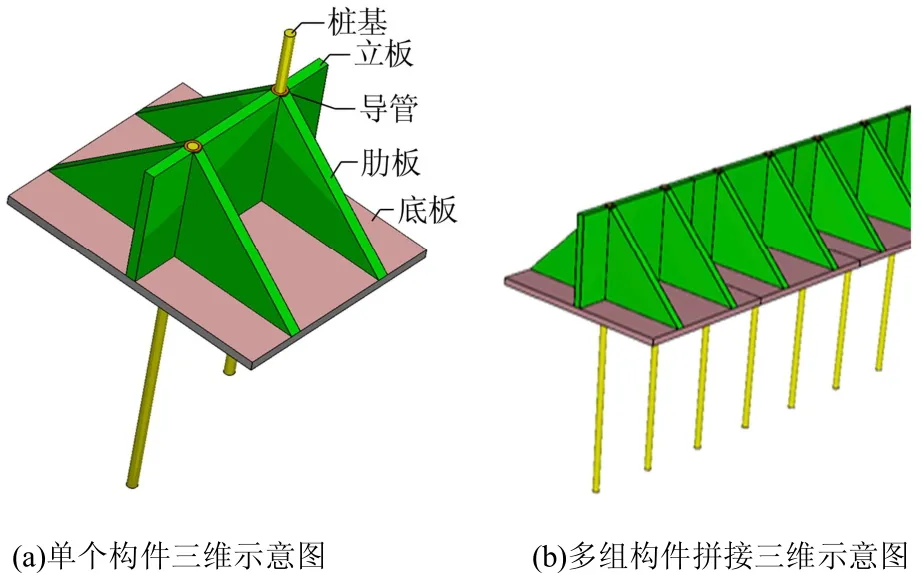
图1 倒T 型导管墙桩基防波堤三维示意图 Fig.1 3D model of the inverted T-type breakwater with jackets and pile foundations

2 有限元分析方法

有限元法不仅满足极限平衡分析中的平衡条件、破坏条件、变形协调条件，还考虑了土的应力—应变特性、土与结构的相互作用，目前已广泛应用于边坡稳定性分析、地基承载力分析、结构稳定性分析等[5]。通过建立弹塑性有限元模型，分析倒T 型导管墙桩基防波堤桩基与土的作用机制和失稳模式，为稳定性的简化计算提供依据。

2.1 有限元模型

图2 给出了该结构的有限元计算域示意图。该结构在受力上具有明显的空间特性，在波浪载荷垂直于防波堤轴线墙时，一组构件关于与波浪方向平行的平面对称。为提高计算效率，选取一组构件的1/2 作为分析对象。在建立的三维有限元模型中，土体与结构均采用8 节点三维减缩积分实体单元，在结构与土体相互作用区域建立主从接触面。T 型导管墙桩基防波堤结构与土体的接触面主要包括底板与土体的接触面和桩基与土体的接触面，考虑到结构弹性模量远大于土体弹性模量，所以指定结构接触面为主接触面，土体接触面为从接触面。接触面本构模型在切向方向采用库仑摩擦本构模型（摩擦系数为0.3），法向采用硬接触方式。倒T 型导管墙桩基防波堤结构弹性模量较大，且各部分连接牢固，有限元分析中对其进行整体弹性模型建立，土体采用ABAQUS有限元软件的Mohr-Coulumb 塑性模型[6]。

图2 结构有限元计算域 Fig.2 Finite element computational domain

2.2 水文条件

在建立倒T 型导管墙桩基防波堤有限元模型时，选取一组较典型的水深波浪条件，见表1。在计算波浪力时，采用《海港水文规范》[7]中平面直立墙波浪力的计算方法，直立墙所受的波浪力分布简图如图3 所示。波浪中线超出静水面的高度 sH 可按下式确定：

式中：Hd为设计波高；d 为水深；L 为波长。静水面以上某高度处波浪压力强度为0，通过计算，得到倒T型防波堤静水面Hs+Hd高度处波浪压力强度为0。水底处波浪压力强度3p 可按下式计算：

式中：γ 为水的重度。根据表1 数据，得到防波堤水底处波浪压力强度3p 为35.58 kPa。静水面处波浪压力强度2p 可按下式计算：

计算得出防波堤静水面处波浪压力强度为53.67 kPa。防波堤堤顶高于静水面3.5m，得出堤顶波压强度1p 为24.99 kPa，

即

最终得到在设计高水位波峰情况下防波堤结构承受的波浪载荷，见图4。

表1 水文条件 Table 1 Hydrological conditions

图3 波峰作用时直立墙波浪力分布简图 Fig.3 Distribution of wave force of vertical wall under the wave peak

图4 设计高水位波峰时防波堤波浪力分布图 Fig.4 Distribution of wave force under the wave peak at design water level

本文条件近似选取天津港地区的原始土层参数（即地基未经处理的数据），见表2。地基土层由上至下共5 层，依次为淤泥层、淤泥质黏土层、粉质黏土层、粉土层和粉砂层。其中淤泥层的厚度较大，在实际工程应用中应考虑地基的处理问题。

表2 各土层主要参数 Table 2 Properties of soil layers

2.3 结构稳定性与失稳模式

有限元计算过程中，逐步增加波浪力，计算不同加载情况下的结构位移。位移主要包括抗滑稳定性分析的水平位移及抗倾稳定性分析的结构立板转角。为了建立有限元计算参数与结构安全系数的关系，引入加载系数α 表征加载程度[8]，对其进行无量纲化处理：

式中：P 为计算时施加的荷载；DP 为设计波浪荷载。结构达到极限承载状态，即P 加载到极限承载力Pm时，结构稳定性安全系数K 可以用加载系数α 表示。

图5 给出了不同桩基入土深度下波浪力-位移关系曲线。根据失稳判别标准Ⅰ，结构达到极限承载状态时，波浪力加载系数-位移关系曲线斜率接近0 时所对应的波浪力即极限承载力，渐近线对应的加载系数α 即为结构稳定性安全系数K。表3 给出了不同结构尺寸的安全系数，其中结构尺寸是在入土深度为20 m，桩径为1.0 m，肋板间距为3 m，底板宽度为16 m 基础上进行变化的。通过表中数据可以看出，同一结构尺寸下波浪力-水平位移曲线与波浪力-转角曲线的安全系数基本相同。

图5 不同桩基入土深度下波浪力加载系数-位移关系曲线 Fig.5 Wave force vs. displacement curves at different depths of pile

表3 不同结构尺寸下的安全系数 Table 3 Safety factors for different structure sizes

图6 为结构达到极限承载状态时的位移场分布图，可以看出，构件的位移量自下而上逐渐增大，结构绕桩基背浪侧与底板所形成区域内偏离桩基轴线的某一点转动。因此，倒T 型导管墙桩基防波堤在极限状态下，失稳模式为绕构件底板底面以下某一点发生转动失稳破坏。

图6 极限状态下结构的位移场分布图 Fig.6 Displacement field in the limit state

3.508×1002.665×1001.823×1009.797×10-11.370×10-1

3 稳定性简化计算方法

3.1 抗滑稳定性简化计算

以单个倒T 型导管墙桩基防波堤构件的1/2 作为分析对象，建立构件在滑移情况下的受力分析，如图7 所示。在抗滑稳定性分析中考虑的作用力主要有结构自身的重力G、结构底板底部摩擦力1τ 、结构底板底部波浪浮托力uP 、设计波浪力DP 和桩侧土压力SP 。当底板底部摩擦力1τ 和桩侧土压力SP达到最大值时，结构将发生滑动破坏，即达到抗滑极限状态，此时结构所承受的极限波浪力P 为， KS为抗滑稳定性安全系数。极限状态下作用于结构底板底部的水平摩擦力τ1为

式中：μ 为构件底板与基床间的摩擦系数；uP 根据直墙式建筑物波浪浮托力公式计算。图7 转动点距地基表面竖直距离为Ls，且偏离桩轴线一定距离，根据图6 有限元结果可知，转动点与桩轴线的水平距离很小，对抗滑稳定性影响不大，为了简化计算，忽略转动点与桩的距离，建立水平力平衡方程和力矩平衡方程分别如下：

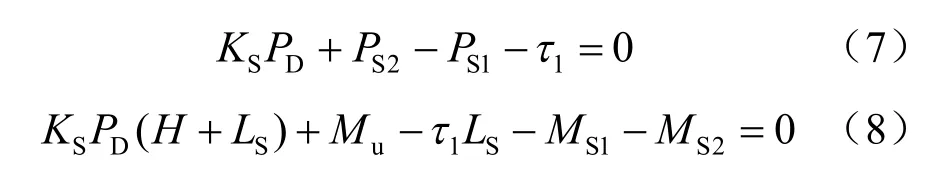
式中：H 为波浪力合力作用点至地基表面的距离；SL 为转动点至地基表面的距离；S1M 和 S2M 为桩侧土压力对转动点的抗倾力矩；uM 为波浪浮托力对转动点的倾覆力矩，且有

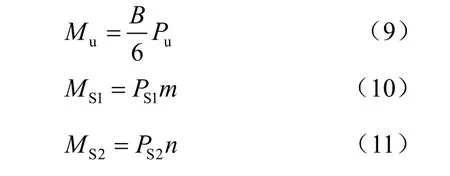
式中：B 为结构底板宽度；m 和n 分别为土压力S1P和S2P 对转动点的力臂，它们是关于SL 的未知量。将式（9）～（11）代入方程式（8）可以整理得到：

式（7）和式（12）只有2 个未知量SL 和 SK ，将其联立求解，即可得到结构的抗滑稳定性安全系数 SK ，将简化方法与有限元方法进行比较，结果见表4。可见，该抗滑稳定性简化算法得到的结果比有限元结果稍大，但误差很小，满足精度要求。

图7 结构抗滑稳定性分析简化模型 Fig.7 Simplified model for anti-sliding analysis

表4 抗滑稳定性简化算法与有限元结果对比 Table 4 Comparison between anti-sliding safety factors with those calculated by FEM

3.2 抗倾稳定性简化计算

以单个倒T 型导管墙桩基防波堤构件的1/2 作为分析对象，建立构件在倾覆情况下的受力分析，如图8 所示。在抗倾稳定性分析中应考虑的作用力有结构自身的重力G、结构底板底部摩擦力1τ 、结构底板底部波浪浮托力uP 、结构底板底部土反力1R 、桩侧摩擦力2τ 、设计波浪力DP 和桩侧土压力SP ，其中波浪浮托力uP 的分布与图6 相同，1τ 、uP和SP 的计算方法与抗滑简化模型相同。作用于结构的桩侧摩擦力2τ 为

式中：f 为土体对桩侧单位面积上的摩擦力，根据美国API 规范，f 不大于黏土不排水剪切强度uc ，最大可以取值uc ；A 为桩侧与土体的接触面积。 API 规范规定，黏性土最大端阻应力可以取为9 倍的黏土不排水剪切强度uc ，因此，结构底板底部土反力1R 的值可以取为

结构在达到极限抗倾状态时，所能承受的极限波浪力P 即为0DK P ，0K 为抗倾稳定性安全系数。根据图8 所示的分析模型，各作用力对转动点O 的力矩平衡方程可写为

式中：H为波浪力合力作用点至地基表面的距离；1L为转动点至地基表面的距离；SM 为桩侧土压力对转动点O 的抗倾力矩；RM 为结构底板底部土反力1R 对转动点O 的抗倾力矩；GM 为结构自重对转动点O 的抗倾力矩；f1M 为结构底板处摩擦力对转动点O 的抗倾力矩；f2M 为桩侧摩擦力对转动点O 的抗倾力矩；uM 为波浪浮托力对转动点O 的倾覆力矩。RM 、GM 、f1M 、f2M 、uM 可以进一步由下列公式表示：

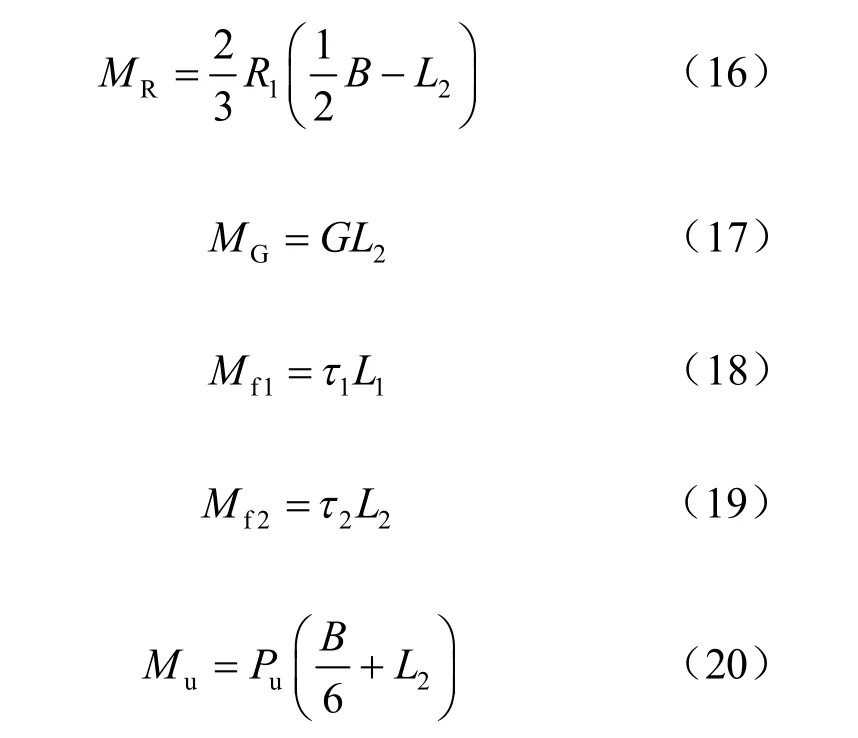
其中：B 为结构底板的宽度；2L 为转动点O 至桩基轴线的距离。在确定结构转动点的位置即1L 、2L 后，则可以得到倒T 型导管墙桩基防波堤的抗倾稳定性安全系数0K 为

有限元分析发现，随着底板宽度B 增加，2/L B基本呈线性增长，见表5，采用线性函数对数据进行拟合可得

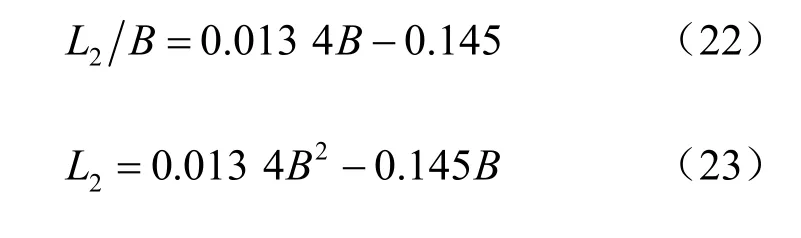
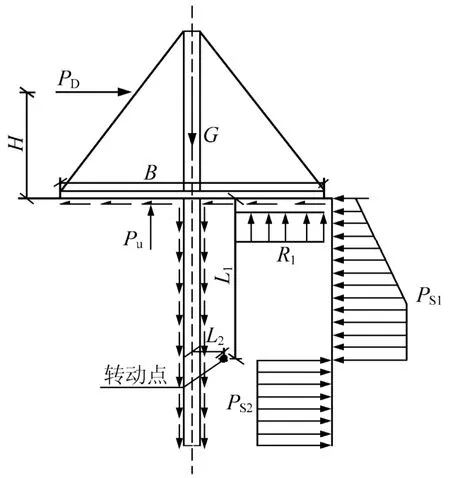
图8 结构抗倾稳定性分析简化模型 Fig.8 The simplified model for anti-overturning analysis

表5 不同底板宽度B 下L2值 Table 5 The values of L2 for different bottom width B

表6 抗倾稳定性简化算法与有限元结果对比 Table 6 Comparison between anti-overturning safety factors with those calculated by FEM

本文采用极限平衡法确定转动点距地基表面的距离1L 。结构在达到极限抗倾状态时，结构的水平力平衡方程和力矩平衡方程分别如下： 整理得到转动点至地基表面的距离1L 。1L 、2L 确定后，可以通过式（21）得到简化算法抗倾稳定性安全系数0K ，该方法与有限元分析结果进行比较，结果见表6。结果表明，不同结构尺寸下，依据抗倾稳定性简化算法得到的结果略小于有限元结果，但误差较小。

另需说明的是，本文将抗滑和抗倾稳定性作为两种不同的极限状态分别考虑，故图7、8 的转动点是不一致的。

4 结 论

倒T 型导管墙桩基防波堤是一种新型港口与海岸工程结构型式，尚未建立其稳定性设计与计算方法。本文对该新型结构的稳定性进行了三维有限元分析，并结合有限元分析结果，提出稳定性简化算法。限于篇幅，没有给出桩的内力分析结果。

（1）建立有限元分析模型，根据波浪力-位移关系曲线及失稳判别标准1，得出结构稳定性安全系数；结构在极限状态下的失稳模式为绕底板底面下偏离桩基轴线的某一点发生转动失稳。

（2）在有限元分析基础上，结合现有规范和极限平衡理论，建立了倒T 型导管墙桩基防波堤稳定性的简化计算方法。该方法计算简单，与有限元计算结果较为吻合，具有较好的计算精度。

[1] 杨家岭， 王书法， 孔令伟， 等. 桶形基础采油平台三维有限元稳定性计算分析[J]. 岩土力学， 2002， 23(5)： 641－644. YANG Jia-ling， WANG Shu-fa， KONG Ling-wei， et al. The 3-D finite element analysis of stability of platform with bucket foundation[J]. Rock and Soil Mechanics， 2002， 23(5)： 641－644.

[2] 孟昭瑛， 梁子冀， 刘孟家. 浅海桶形基础平台水平承载力与抗滑稳定分析[J]. 黄渤海海洋， 2000， 18(4)： 37－40. MENG Zhao-ying， LIANG Zi-ji， LIU Meng-jia. Analysis of horizontal bear capacity and stability against sliding of bucket foundation platform[J]. Journal of Oceano- graphy of Huanghai & Bohai Seas， 2000， 18(4)： 37－40.

[3] 肖忠， 王元战， 及春宁， 等. 筒型基础防波堤稳定性有限元数值分析[J]. 土木工程学报， 2009， 42(7)： 122－124. XIAO Zhong， WANG Yuan-zhan， JI Chun-ning， et al. Finite element analysis of the stability of bucket foundation breakwater[J]. China Civil Engineering Journal， 2009， 42(7)： 122－124.

[4] 王元战， 肖忠， 迟丽华， 等. 筒型基础防波堤稳定性简化计算方法[J]. 岩土力学， 2009， 30(5)： 1368－1370. WANG Yuan-zhan， XIAO Zhong， CHI Li-hua， et al. A simplified calculation method for stability of bucket foundation breakwater[J]. Rock and Soil Mechanics， 2009， 30(5)： 1368－1370.

[5] 庄茁， 由小川， 廖剑晖. 基于ABAQUS 的有限元分析与应用[M]. 北京： 清华大学出版社， 2009.

[6] HKS INC. ABAQUS analysis user’s manual[M]. USA： HKS Company， 2004.

[7] 中华人民共和国交通部. JTJ213－98 海港水文规范[S]. 北京： 人民交通出版社， 1998.

[8] 王刚， 陈杨， 张建民. 大圆筒结构倾覆稳定分析的有限元法[J]. 岩土力学， 2006， 27(2)： 238－241. WANG Gang， CHEN Yang， ZHANG Jian-min. Finite element method for analyzing overturn stability of large cylindrical structures[J]. Rock and Soil Mechanics， 2006， 27(2)： 238－241.