隧道水平冻结施工引起地表冻胀的历时预测模型
2012-01-08蔡海兵彭立敏郑腾龙
蔡海兵 ,彭立敏郑腾龙
(1.中南大学 土木工程学院,长沙 410075;2.安徽理工大学 土木建筑学院,安徽 淮南 232001)
1 引 言
地铁隧道采用人工冻结法辅助施工时,在冻结壁形成过程中,随着地层温度的下降,土体温度达到冰点,伴随土中孔隙水和迁移水的结晶体、透镜体、冰夹层等形成的冰侵入土体,引起土体体积膨胀,进而在地表产生冻胀现象[1]。地铁隧道冻结施工期的冻胀现象将对工程周围环境产生不良影响。因此,在隧道冻结工程设计阶段,应根据具体工程性质,采用合理方法对可能引起的地表冻胀变形进行预估,以便于实际施工过程中采取适宜的冻结实施方案及相应的冻胀预防措施。
波兰学者Litwiniszyn[2]基于砂箱模型试验,为研究地下采矿过程中岩层与地表移动等问题而提出了随机介质理论。该理论经过我国学者[3-5]多年的发展和完善,目前已成为我国城市地铁隧道工程中地表变形预测的实用方法之一。如将地层冻结引起的地表冻胀变形看成是一随机过程,该过程可以认为是岩土体开挖引起地表变形的逆过程,则隧道冻结施工引起的地表冻胀变形问题亦可以采用随机介质理论进行预测分析。现有相关方面的研究主要为:阳军生等[3]采用随机介质理论,推导了隧道地层冻结引起的地面冻胀变形的计算公式;陶德敬等[6]应用随机介质理论,对北京地铁“复—八”线“大北窑——热电厂”区间隧道冻结时的地表冻胀变形进行了计算分析;周太全等[7]针对南京地铁某区间隧道冻结法施工工程,采用随机介质理论对该工程的冻胀效应进行预测,具体分析了水平冻胀引起的地面隆起、曲率变形规律;李方政[8]采用随机介质理论,以上海体育场穿越工程为研究背景,运用叠加法基本原理,推导出多管冻结的地层冻胀叠加法表达式。
上述研究得出了一些有意义的结论,但共同的不足之处是分析过程中均未考虑冻结过程,即冻结壁的形成过程:开始冻结时,低温盐水与冻结管周围的地层产生剧烈的热交换,在每个冻结管周围很快形成近似圆柱形的冻结岩土柱,如图1(a);冻土柱进一步扩展,直至相邻冻土柱相互交圈,在隧道周围形成封闭的冻结壁,如图1(b);交圈后,原各冻结管的冻结锋面连成向隧道内扩展的内冻结锋面和向隧道外扩展的外冻结锋面,且内、外冻结锋面很快趋于平滑,如图1(c)。
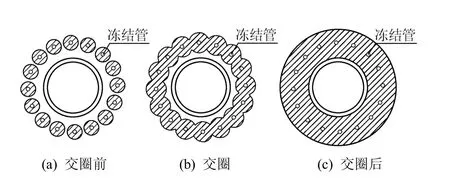
图1 冻结壁形成过程 Fig.1 The formation process of frozen wall
本文考虑冻结过程,基于随机介质理论,以圆形隧道全断面水平冻结为例,建立隧道水平冻结施工引起地表冻胀位移的历时预测模型。
2 单管冻结引起地表冻胀的计算模型
如图2 所示,考虑隧道单根冻结管冻结的情况,冻结管编号记为1,该冻结管中心在εοη(x zο )直角坐标系下的横坐标为1x ,纵坐标为1z 。冻结岩土柱呈圆柱状由冻结管向外扩展,经t 时刻后,冻土柱的外半径发展至 R ( t )。冻土柱在形成过程中发生的体积膨胀假定为冻土柱从半径 R ( t )均匀膨胀至RΔ,膨胀的圆环柱截面积记为Δ。根据随机介质理论,对于平面问题,在εοη(xο z)直角坐标系下,隧道单管水平冻结情况下地表各点冻胀位移表达式为
因积分区域为圆环形,将直角坐标系转换成 极坐标系会更有利于求解。坐标系分两次转换,如图2(a),首先将εοη(xο z)直角坐标系转换成 ε1ο1η1直角坐标系,如图2(b),再将 ε1ο1η1直角坐标系转换成 r1ο1θ1极坐标系。
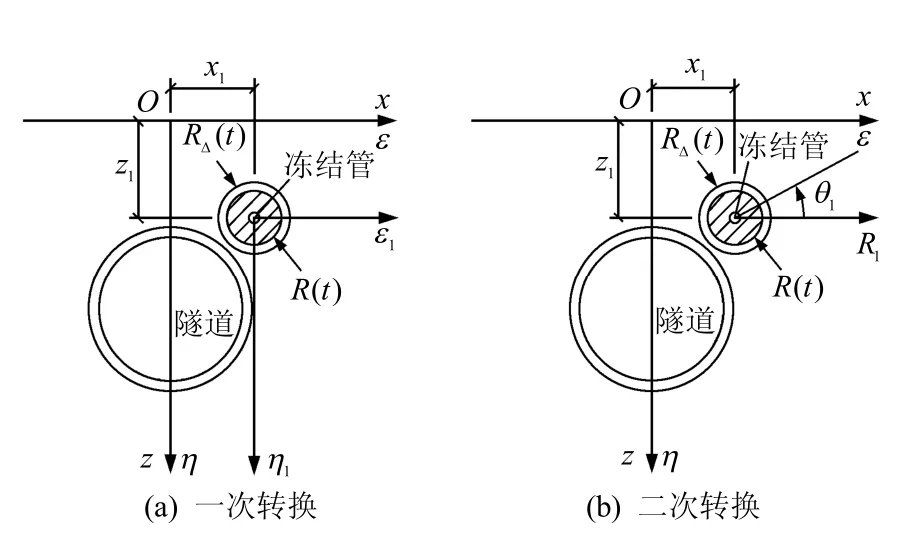
图2 单管冻结坐标系转换图 Fig.2 Coordinate system transformation of single pipe freezing
则εοη(x zο )直角坐标系变换到111rο θ 极坐标系的转换公式为

根据双重积分的换元公式,在111rο θ 极坐标系下式(1)可写为
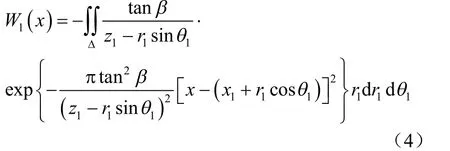
圆环形积分区域Δ 的内半径为 R ( t ),外半径为RΔ,则上式又可变为
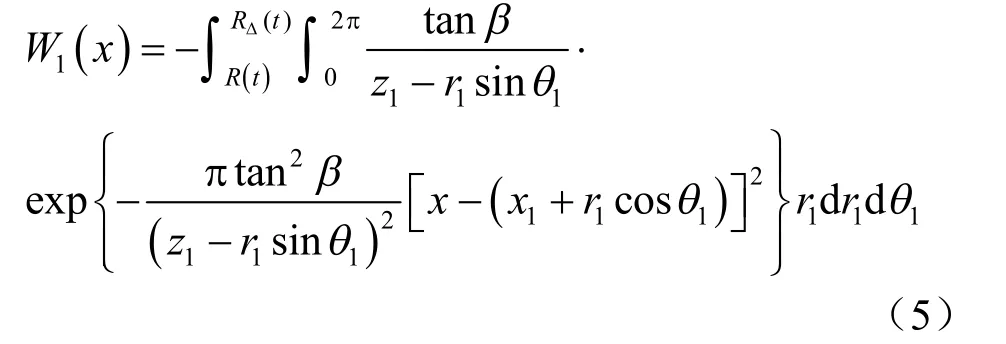
式中:x 为在εοη (x zο )直角坐标系下地表各点的横坐标;1x 、1z 为在εοη(x zο )直角坐标系下冻结管中心的横、纵坐标;1r、1θ 为在111rο θ 极坐标系下的极径、极角;β 为冻土柱上覆岩土层的主要影响角。
对于平面问题,在111rο θ 极坐标系下,式(5)即为隧道单管水平冻结引起地表各点冻胀位移的表达式。
3 多管冻结引起地表冻胀的历时预测模型
3.1 冻结壁交圈前的历时预测模型
假定隧道采用单圈多管全断面水平冻结,以n根冻结管均匀布置在同一设计圈径上,各冻结管所处的土层性质相同,且不考虑冻结孔实际造孔过程中的偏斜影响,由冻结壁的形成过程(见图1)可知,冻结壁交圈前,经t 时刻后,在隧道周边形成n个外半径为 R ( t )的冻土柱,各冻土柱形成过程中发生的体积膨胀均为从半径 R ( t )均匀膨胀至RΔ,膨胀的各圆环柱截面积也均为Δ。如忽略相邻冻结管冻结引起地表冻胀位移的相互影响,则在冻结壁交圈前,地表冻胀由多个冻土柱的叠加膨胀变形引起,此时地表冻胀位移可视为单管水平冻结引起地表冻胀位移的叠加问题。
记各冻结管的编号为1、2、…、n,则第i 根冻结管中心在εοη(xο z)直角坐标系下的横坐标为 xi,纵坐标为 zi,其计算公式分别为
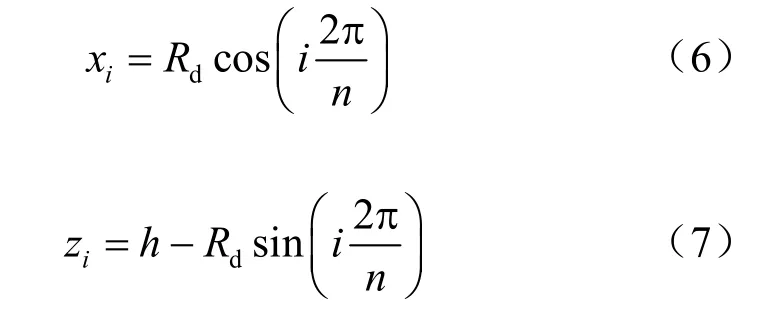
式中:h 为隧道中心距地表的距离,即隧道埋深;dR为冻结管布置圈半径。
在计算第i 根冻结管水平冻结引起地表各点冻胀位移之前,都需要将εοη(x zο )直角坐标系变换到iiirο θ 极坐标系,其转换公式为
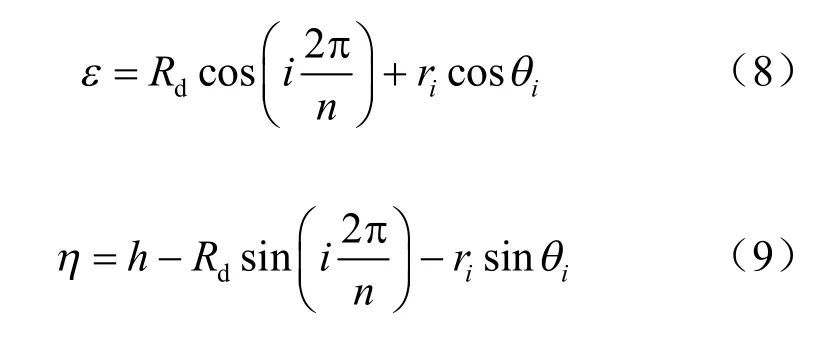
由式(5)可得在平面问题条件下第i 根冻结管水平冻结引起地表各点冻胀位移表达式为

根据叠加原理,则有冻结壁交圈前多管水平冻结引起的地表冻胀位移表达式为
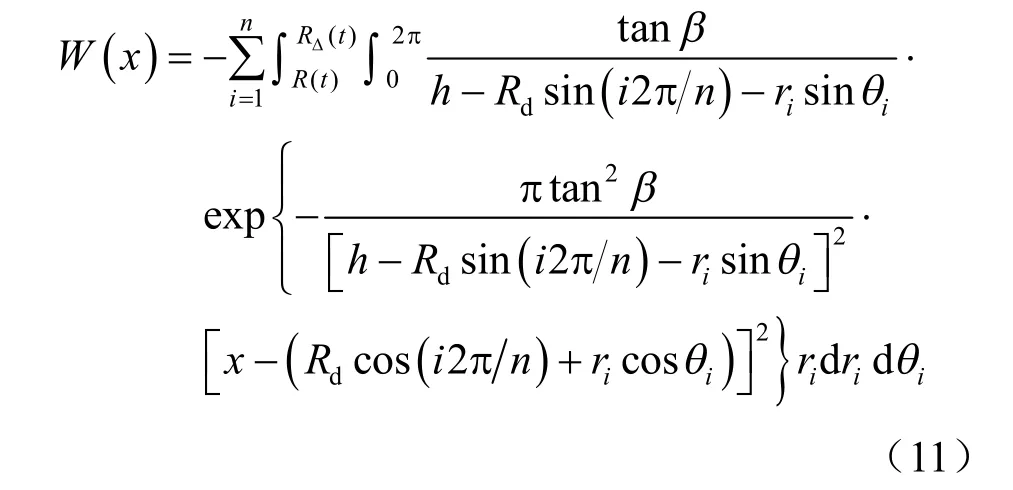
3.2 冻结壁交圈后的历时预测模型
随着冻结时间的延长,隧道周边各冻土柱进一步扩展,相邻冻土柱相互交圈后即在隧道周边形成圆环柱状冻结壁,且冻结壁的内、外冻结锋面很快趋于平滑。如图3 所示,经t 时刻后,冻结壁已交圈,以隧道中心为圆心,冻结壁外锋面半径为 R ( t ),冻结壁扩展过程中的体积冻胀假定为从半径 R ( t)均匀膨胀至RΔ,冻胀区域面积为Δ。冻结壁交圈后,地表冻胀则由整个冻结壁的膨胀变形引起,此时地表冻胀位移计算类似于单管水平冻结情况的求解方法。
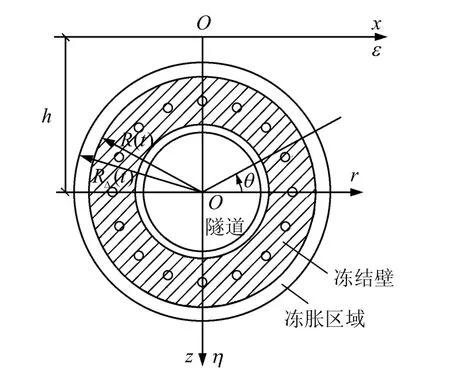
图3 冻结壁交圈后多管冻结坐标系转换图 Fig.3 Coordinate system transformation of multiple pipes freezing after the circle-crossing period of frozen wall
将εοη(x zο )直角坐标系转换成rο θ′ 极坐标系,则该两坐标系之间的转换公式为
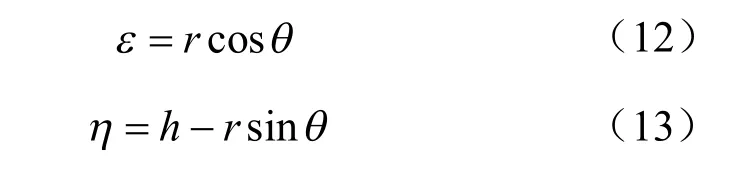
根据双重积分的换元公式,在rο θ′ 极坐标系下式(1)可写为
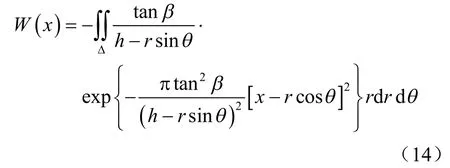
冻胀区域Δ 的内半径为 ( )R t ,外半径为RΔ,则上式又可变为

式中:r、θ 为在rο θ′ 极坐标系下的极径、极角。
对于平面问题,在rο θ′ 极坐标系下,式(15)即为冻结壁交圈后多管水平冻结引起地表各点冻胀位移的表达式。
当隧道采用全断面水平冻结法施工时,考虑冻结壁的形成过程,交圈前采用式(11)计算地表各点冻胀位移,交圈后则采用式(15)计算地表各点冻胀位移。
上述地表冻胀预测模型在应用过程中,当隧道埋深h、冻结管布置圈半径 Rd、冻结管根数n 和岩土层主要影响角β 等参数已知,对于地表冻胀位移的计算还需确定的参数为t 时刻冻结外锋面半径R ( t )、和冻土柱(交圈前)或冻结壁(交圈后)的冻胀区域外半径RΔ,下述对该2 个参数的确定方法进行讨论。
3.3 冻结外锋面半径的确定方法
在冻结壁交圈前,冻结外锋面半径 R ( t )为单个冻土柱的半径,在冻结壁交圈后,则为冻结壁外锋面半径。冻结壁交圈前、后冻结外锋面半径的确定问题即为单管冻结和多管冻结条件下温度场分布规律的求解问题。人工冻结温度场是一个有相变、移动边界、内热源以及边界条件复杂的瞬态导热问题,其精确求解过程较为复杂。
地铁隧道冻结工程中,一般均需在冻结区域布设测温孔,在冻结施工中可根据测温孔内的测点温度数据实时反演冻结温度场。某特定时刻的冻结温度场分布规律和冻结锋面位置可由特鲁巴克或巴霍尔金提出的稳态温度场计算方法求得[9]。但这不便于冻结施工前的温度场预测分析。
由现有考虑相变的单管冻结温度场(二维热传导问题)和平板冻结温度场(一维无限域热传导问题Neumann 解)的瞬态解析结果可知[10-11],多管冻结交圈条件下冻结壁的扩展厚度(单管冻结条件下的冻土柱半径)与冻结时间的平方根成正比,可采用下述公式表示:

式中:E ( t )为冻结壁扩展厚度或冻土柱半径(mm);A 为待定常数;t 为冻结时间(d)。
冻结壁交圈后的温度场可由平板冻结理论近似求解,该理论中常数A 由下式给出:

式中:α1、 α2为冻土、未冻土的热扩散系数; k1、k2为冻土、未冻土的导热系数;T0为土体初始温度;Tc为冻结源温度;Ψ 为单位容积土体的结冰潜热;Φ( y)为高斯误差函数,且有:
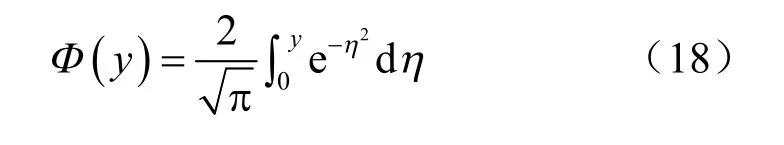
冻结壁交圈前的温度场可由单管冻结理论进行求解,该理论中常数A 的计算公式详见蒋斌松等[10]的推导结果。可见当土体热物理参数由室内试验获取后,常数A 可由解析方法求得。
常数A 也可通过冻结温度场的现场实测数据进行回归分析并按经验取值,李方政[8]根据工程经验,认为A 可取160;唐益群等[12]鉴于上海隧道一般位于第④层饱和淤泥质黏土层中,通过室内试验得到该土层的常数A 可取152.5;陈湘生等[13]基于上海地区地铁联络通道水平冻结温度场实测数据,回归分析得出常数A 取150。
在冻结壁交圈前,冻结壁扩展厚度 E ( t )即为单管冻土柱半径 R ( t );冻结壁交圈后,若已知冻结管布置圈径 Rd,则冻结外锋面半径 R ( t )、内锋面半径 R1( t )可按下式进行计算:
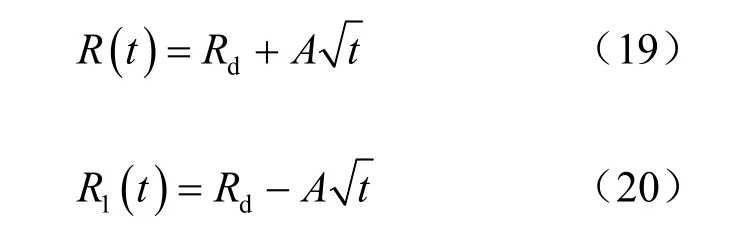
根据相关研究[13],冻结壁轴面上冻土柱扩展速度一般比主面上要快10%~20%,则冻结壁交圈时间可用下述公式计算:
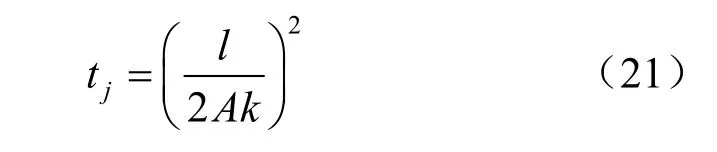
式中:jt 为冻结壁交圈时间(d);l 为相邻冻结管间距;k 为经验系数,可取1.1~1.2。
3.4 冻胀区域外半径的确定方法
工程中反映土体冻胀强弱的指标一般采用冻胀率,是指土体试样在无侧向变形、无纵向荷载条件下,经单向冻结,其纵向的高度增量与试样原高度的比值,如下式:

式中:hε 为土体冻胀率; hΔ 为试样纵向冻胀量;h为试样原高度。
刘鸿绪[14]认为,土体冻结过程中某点的冻胀量是该点之下冻结土层冻胀率沿冻层厚度的积分,与冻胀力无直接联系。据其原理,假定冻结壁向外均匀膨胀,考虑冻结过程,则有:
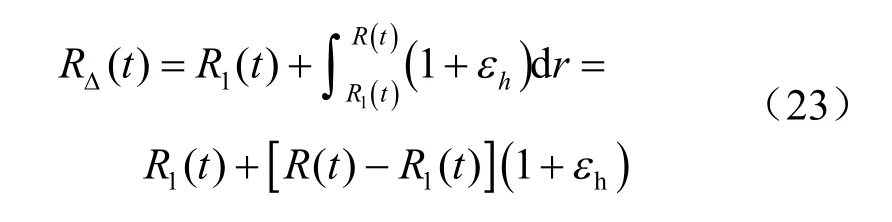
若考虑冻结过程,即冻结锋面随时间增长的发展过程,综合式(19)、(20)和(23)可确定特定时刻t 的冻胀区域外半径RΔ。
4 工程案例1
以某地铁隧道全断面水平冻结施工工程为例,该隧道断面为圆形,隧道外半径为3 m,埋深为 15 m,水平冻结管布置圈半径为4 m,共布置冻结管20 根,冻结管直径为160 mm,相邻管间距为 1.25 m,土体冻胀率为1%,岩土层主要影响角度的正切值tan β 取0.8。
按经验取常数 150A= 、 1.1k= ,根据式(21),冻结壁的交圈时间为14.3 d。
冻结壁交圈前,单个冻土柱内半径为冻结管半径,即 R1=80 mm,根据式(16)计算冻土柱外半径为 R ( t )= 150tmm;冻结壁交圈后,根据式(19)和(20),可确定冻结壁外、内锋面半径。冻结壁交圈前、后冻胀区域外半径根据式(23)计算。
地表计算区域选为 -2 0 m ≤ x≤ 20 m,根据Legendre-Gauss 积分方法,采用Maple 数学软件编制计算程序,得到地表冻胀位移分布规律随冻结时间的变化曲线如图4 所示。
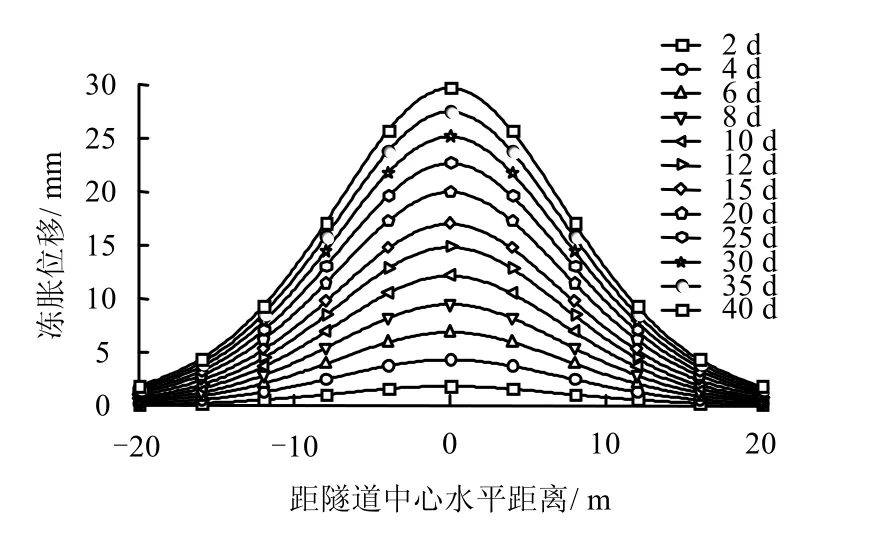
图4 地表冻胀位移分布规律随时间变化曲线 Fig.4 Variations of surface frost heave displacements distribution with time
由图4 可知,对于任意时刻地表最大冻胀位移均发生在隧道中心正上部(距隧道中心水平距离 0 m),且随着距隧道中心越远,地表冻胀位移逐渐减小并最终趋于0。在冻结初期,地表冻胀现象不明显,如冻结4 d 后,地表最大冻胀位移仅为4.3 mm,随着冻结时间的延长,地表冻胀现象增强,各点的冻胀位移均逐渐增大,冻结40 d 后,地表最大冻胀位移达到29.6 mm,距隧道中心水平距离12 m 处的地表冻胀位移也达到9.3 mm。总的来说,隧道水平冻结施工中诱发的地表冻胀现象与冻结过程密切相关,随着冻结时间延长,冻结壁变厚,地表冻胀位移逐渐增大。在现有隧道冻结施工冻胀效应的随机介质理论分析成果中[6-7],均未考虑冻结壁的发展过程,如直接将冻胀理论计算值与现场实测值进行比较,此举不符合实际情况。
图5 给出了距隧道中心水平距离分别为0、2、4、8、12、16、20 m 的地表各点冻胀位移随冻结时间(共40 d)的变化曲线。
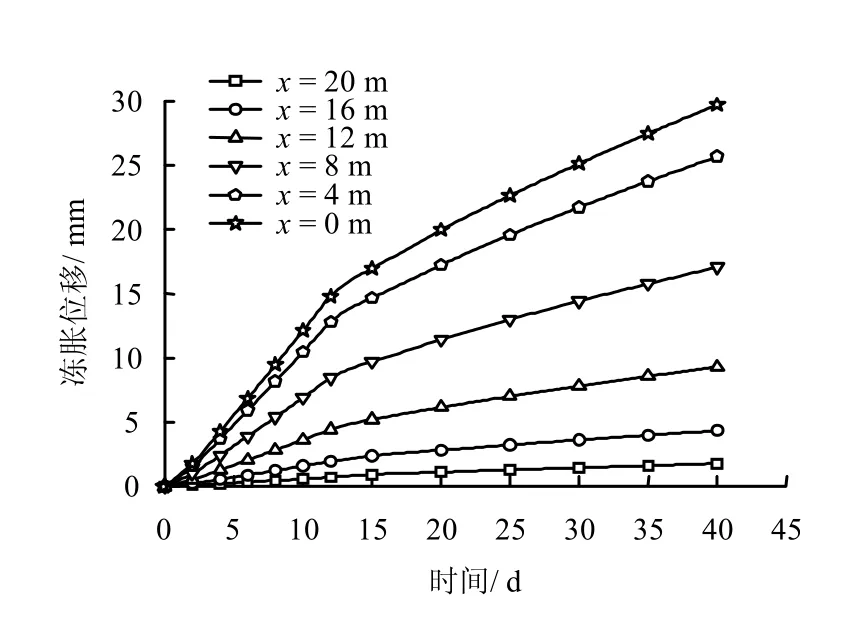
图5 地表各点冻胀位移随时间变化曲线 Fig.5 Variations of surface frost heave displacements with time
冻结壁的交圈时间经计算约为14 d,无论在冻结壁交圈前,还是在冻结壁交圈后,地表冻胀位移增长速度均随着距隧道中心越远而变小,且冻胀位移均随时间呈增长趋势。地表各点冻胀位移随时间变化曲线反映出冻胀与冻结壁的交圈时间存在着密切的联系,在冻结初期,冻结壁尚未交圈,冻胀位移增长速度较快,隧道中心正上部( 0x= )地表冻胀位移增长速度达到1.23 mm/d;冻结壁交圈之后,冻胀位移增长速度减缓,隧道中心正上部( 0x= )地表冻胀位移增长速度约为0.5 mm/d。地表冻胀与冻结壁交圈时间的关系分析结果与相关模型试验结果一致[15]。
5 工程案例2
广州地铁3 号线天河客运站站后折返线隧道为五心圆拱双线隧道,隧道宽为11.4 m,高为9.12 m,长为138.8 m,埋深为8~10 m,属浅埋大断面隧道。隧道施工采用全断面冻结帷幕+CRD 暗挖工法,支护结构采用复合式衬砌。隧道水平冻结长度为 138.8 m,分南、北两段施工。南、北端均在距隧道开挖边界1 m 处沿五心圆拱线型各布置一圈冻结孔,每端共计46 个冻结孔,冻结孔间距为700~ 950 mm,如图6 所示。设计冻结壁厚度为2.5 m,冻结壁平均温度为-8 ℃,该工程为国内迄今采用人工冻结法施工最长的地铁隧道工程。

图6 隧道北端冻结孔设计图(单位:mm) Fig.6 The freezing hole design at northern end of the tunnel (unit: mm)
该工程积极冻结期约为150 d,工程现场沿隧道中心线布置了若干个地表变形测点,监测得到了一系列地表冻胀位移数据[16],测点位置处隧道埋深约为10 m,为便于后续理论计算结果与现场实测结果的对比分析,在本次随机介质理论分析中,隧道埋深同样取10 m。
该隧道冻结孔布置圈为五心圆拱线型,为计算方便起见,采用等代圆方法将其简化成圆形,该方法虽具有一定的近似性,但基本可满足工程精度要求。冻结孔布置圈宽度为13.4 m,高度为11.1 m,经计算简化后的冻结孔圆形布置圈半径为6.125 m。46 根冻结管均匀布置,相邻管间距为0.836 m。工程实际选用冻结管为φ 108 mm×8 mm 的低碳钢无缝钢管。
通过在工程施工现场钻孔取样,对具有代表性的土层进行了人工冻土物理力学性能试验,试验得到各层土的冻胀率如表1 所示[17]。
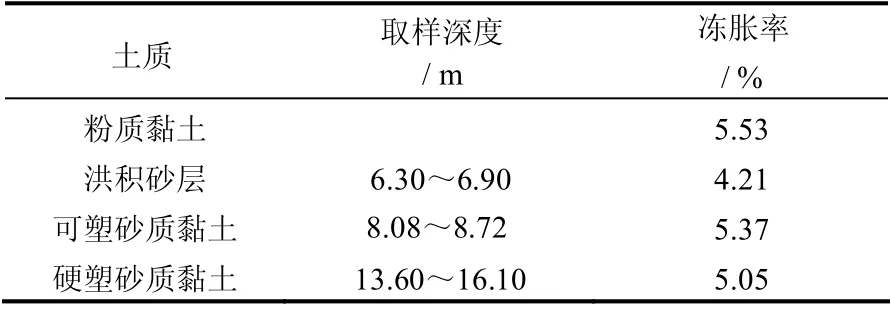
表1 土体冻胀率试验值 Table 1 Experimental values of frost heave rate of soils
该隧道地表冻胀预测分析中,土体冻胀率取表中各土层冻胀率的均值,则为5%。土体主要影响角度的正切值取0.8。按经验取常数 150A= 、k = 1.1。冻结锋面半径与冻胀区域外半径的计算过程同于案例1。
采用已编制的计算程序,得到隧道中心正上部地表冻胀位移随冻结时间(共150 d)的变化曲线,并与现场测试结果相对比,如图7 所示。
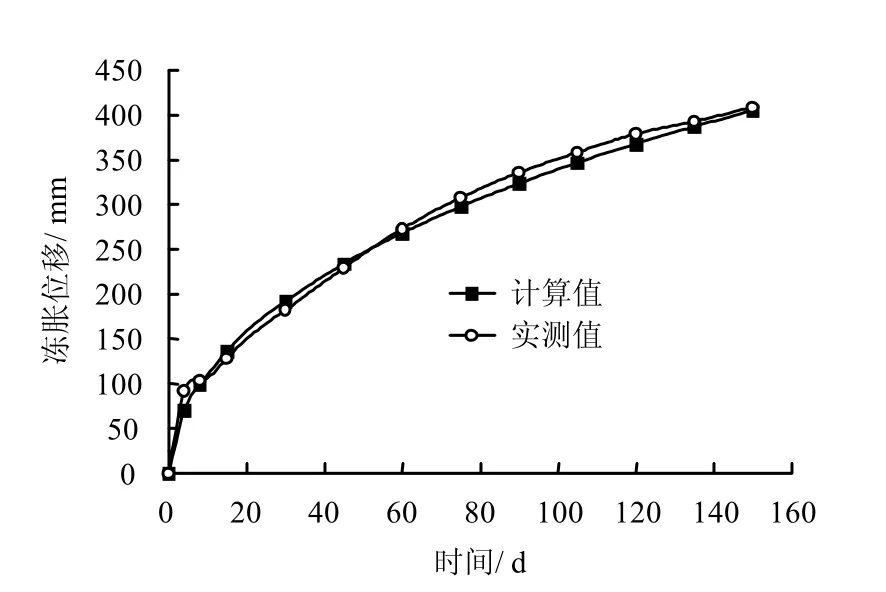
图7 隧道中心正上部地表冻胀位移随时间变化曲线 Fig.7 Variations of surface frost heave displacements with time at the top of tunnel center
由图可知,隧道中心正上部地表冻胀位移随时间变化规律的理论计算和现场实测结果基本一致,在冻结初期,冻胀位移增长速度较快,冻结壁交圈前平均冻胀速度约为17.6 mm/d;而冻结后期,冻胀位移随时间呈相对缓慢增长趋势,冻结壁交圈后平均冻胀速度约为2.1 mm/d。各时间点的冻胀位移计算值和实测值也较为接近,冻结90 d,冻胀位移计算值为323.6 mm,实测值为335.7 mm,两者相差12.1 mm 为分析过程中的最大差值,与冻胀位移值相比,该差值尚可忽略。经冻结150 d 后,该隧道中心正上部地表累计冻胀位移近400 mm。对比分析结果验证了所提出的地表冻胀历时预测模型的可靠性,且该计算模型用于工程实际具有相当的精确性。
在距隧道中心水平距离为20 m 的地表区域,计算得到冻胀位移分布规律随冻结时间的变化曲线如图8 所示,图中仅列出90 d 的计算结果。
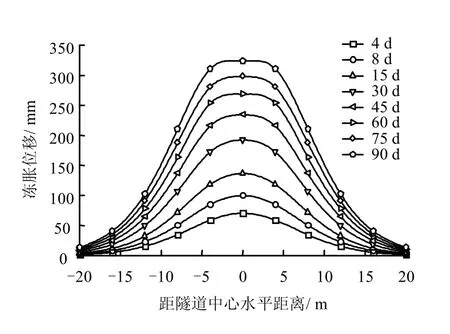
图8 地表冻胀位移分布规律随时间变化曲线 Fig.8 Variations of surface frost heave displacements distribution with time
由图可知,距隧道中心越远,地表冻胀位移逐渐减小,位移增长速度也逐步减缓。在距离隧道中心较近的地表区域,如 -5 m ≤ x ≤ 5 m,随着冻结时间的延长,冻胀位移分布形状由圆拱型逐渐过渡到近水平线型,说明在冻结后期,冻结壁厚度增大,冻土距地表渐浅,巨大的冻胀变形使得隧道中心地表区域产生近似均匀的隆起现象。
该隧道冻结施工期的地表冻胀量较大,主要由多种因素造成,如隧道断面大、埋深超浅;冻土体积大、覆土浅;距离外部环境近,热交换大,导致冻结时间过长;土层大部分为为细致黏土层,且地下水含量大,冻胀系数大等原因。
6 结 论
(1)在隧道多管水平冻结施工中,冻结壁交圈前,地表冻胀位移由多个独立冻土柱的叠加冻胀效应引起,冻结壁交圈后,地表冻胀位移则由整个冻结壁的冻胀效应引起。据此,考虑冻结壁的形成过程,基于随机介质理论,建立了地表冻胀位移的历时预测模型。
(2)具体分析了计算模型中冻结外锋面半径和冻胀区域外半径这2 个关键参数的取值方法。多管冻结交圈条件下冻结壁的扩展厚度(单管冻结条件下的冻土柱半径)与冻结时间的平方根成正比,由此可通过解析或经验方法确定冻结外锋面半径;土体冻结过程中某点的冻胀量是该点之下冻结土层冻胀率沿冻层厚度的积分,由此可根据土体冻胀率、冻结内、外锋面半径确定冻胀区域外半径;岩土层主要影响角决定地表的冻胀范围,其取值问题有待进一步研究。
(3)工程案例分析结果表明,该计算模型用于隧道水平冻结施工引起的地表冻胀位移预测,具有相当的精确性;隧道水平冻结施工中诱发的地表冻胀现象与冻结过程密切相关,随着冻结时间延长,地表冻胀位移逐渐增大;地表冻胀与冻结壁的交圈时间存在着密切的联系,冻结壁交圈前,冻胀位移增长速度较快,冻结壁交圈后,冻胀位移增长速度减缓。
[1] 徐学祖, 王家澄, 张立新. 冻土物理学[M]. 北京: 科学出版社, 2001.
[2] LITWINISZYN J. Fundamental principles of the mechanics of stochastic medium[C]//Proceedings of the 3rd Conference on Theoretical Applied Mechanics. India: [s. n.], 1957: 18-26.
[3] 阳军生, 刘宝琛. 城市隧道施工引起的地表移动及变形[M]. 北京: 中国铁道出版社, 2002.
[4] 施成华, 彭立敏. 随机介质理论在盾构法隧道纵向地表沉降预测中的应用[J]. 岩土力学, 2004, 25(2): 320-323. SHI Cheng-hua, PENG Li-min. Application of stochastic medium theory to predicting settlement in longitudinal surface due to tunnel construction by shield[J]. Rock and Soil Mechanics, 2004, 25(2): 320-323.
[5] 施成华, 彭立敏, 雷明锋. 盾构法施工隧道地层变形时空统一预测方法研究[J]. 岩土力学, 2009, 30(8): 2379-2384. SHI Cheng-hua, PENG Li-min, LEI Ming-feng. Study of time-space united calculating method of stratum deformation caused by shield tunnel excavation[J]. Rock and Soil Mechanics, 2009, 30(8): 2379-2384.
[6] 陶德敬, 王明年, 刘大刚. 冻结法隧道施工引起的地表移动及变形预测[J]. 现代隧道技术, 2006, 43(6): 45-50. TAO De-jing, WANG Ming-nian, LIU Da-gang. Prediction of surface movement and deformation caused by the freezing method construction of tunnels[J]. Modern Tunnelling Technology, 2006, 43(6): 45-50.
[7] 周太全, 华渊, 吕宝华. 某地铁区间隧道冻结施工冻胀效应随机预测分析[J]. 冰川冻土, 2009, 31(1): 119-123. ZHOU Tai-quan, HUA Yuan, LÜ Bao-hua. Stochastic prediction for frost heave effect of a subway tunnel[J]. Journal of Glaciology and Geocryology, 2009, 31(1): 119-123.
[8] 李方政. 土体冻胀与地基梁相互作用的叠加法研究[J]. 岩土力学, 2009, 30(1): 79-85. LI Fang-zheng. Research on superposition method of interaction between soil frost heave and beams on foundation[J]. Rock and Soil Mechanics, 2009, 30(1): 79-85.
[9] 胡向东, 白楠, 余锋. 单排管冻结温度场TPУПAК 和БAXOЛДИH公式的适用性[J]. 同济大学学报 (自然科学版), 2008, 36(7): 906-910. HU Xiang-dong, BAI Nan, YU Feng. Analysis of Trupak and Bakholdin formulas for temperature field of single-row-pipe frozen soil wall[J]. Journal of Tongji University (Natural Science), 2008, 36(7): 906-910.
[10] 蒋斌松, 王金鸽, 周国庆. 单管冻结温度场解析计算[J]. 中国矿业大学学报, 2009, 38(4): 463-466. JIANG Bin-song, WANG Jin-ge, ZHOU Guo-qing. Analytical calculation of temperature field around a single freezing pipe[J]. Journal of China University of Mining & Technology, 2009, 38(4): 463-466.
[11] LUNARDINI V J, VAROTTA R. Approximate solution to Neumann problem for soil systems[J]. Journal of Energy Resources Technology, 1981, 103(1): 76-82.
[12] 唐益群, 洪军, 杨坪, 等. 人工冻结作用下淤泥质黏土冻胀特性试验研究[J]. 岩土工程学报, 2009, 31(5): 772-776. TANG Yi-qun, HONG Jun, YANG Ping, et al. Frost- heaving behaviors of mucky clay by artificial freezing method[J]. Chinese Journal of Geotechnical Engi- neering, 2009, 31(5): 772-776.
[13] 陈湘生. 地层冻结工法理论研究与实践[M]. 北京: 煤炭工业出版社, 2007.
[14] 刘鸿绪. 对土冻结过程中若干冻胀力学问题的商榷[J]. 冰川冻土, 1990, 12(3): 269-280. LIU Hong-xu. Discussion of frost heave mechanics problems in soil freezing process[J]. Journal of Glaciology and Geocryology, 1990, 12(3): 269-280.
[15] 蔡海兵, 程桦, 彭立敏, 等. 地铁双线隧道水平冻结位移场的模型试验[J]. 岩石力学与工程学报, 2009, 28(10): 2088-2095. CAI Hai-bing, CHENG Hua, PENG Li-min, et al. Model test on displacement field of double-route metro constructed with horizontal freezing method[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(10): 2088-2095.
[16] 姜耀东, 赵毅鑫, 周罡, 等. 广州地铁超长水平冻结多参量监测分析[J]. 岩土力学, 2010, 31(1): 158-164, 173. JIANG Yao-dong, ZHAO Yi-xin, ZHOU Gang, et al. Multi-parameter monitoring of frozen soil structure with super-long freezing hole drilling in Guangzhou metro[J]. Rock and Soil Mechanics, 2010, 31(1): 158-164, 173.
[17] 姚直书. 蔡海兵, 程桦, 等. 采用长距离水平冻结暗挖法的浅埋大断面地铁隧道施工技术[J]. 中国铁道科学, 2011, 32(1): 75-80. YAO Zhi-shu, CAI Hai-bing, CHENG Hua, et al. Multi- parameter monitoring of frozen soil structure with super- long freezing hole drilling in Guangzhou metro[J]. China Railway Science, 2011, 32(1): 75-80.
