基于GARCH族模型的VaR与CVaR值的实证与应用

陶 伟

（阜阳师范学院 经济与商业学院，安徽 阜阳 236000）

0 引言

众所周知，如果不能对风险进行测量准确，往往会导致风险管理策略失效。如何构建合适的模型，并以恰当的方法来对测量风险是当前金融研究领域的一个热点课题。1999年学者Arznereta.l提出了相容风险度量,同时,De lbaen亦指出了是不相容的；而Palmqu ist与B asak等人已成功构造出投资组合的模型并通过实证分析,证明了相对可得到更为合理的结果,而则存在误导投资者错误选择高风险的可能,对比,更能够捕捉极端市场条件下市场因子剧烈波动所产生的风险。因此Acerbi(2001)和Stefan(2001)提出用代替作为金融风险的管理工具,的相容性使其成为更加完善的风险管理工具。VaR法和CVaR法作为当前业内较为流行方法，具有简单易懂的特点，而且相对于方差来说，将投资人的损失作为风险更为合理。本文以港交所H股指数期货的收盘价格数据作为实证载体，研究在正态分布、T分布和广义误差分布下GARCH、EGARCH及PARCH模型的VaR值和CVaR值，分别比较出各个模型的优劣。

1 VaR和CVaR的构建模型

1.1 VaR的定义

VaR是资产在确定的目标时段和置信水平下预期的最大资产损失(或者是在最糟糕的情况下的资产损失)。其表达式为：

式中：C为置信水平；ΔP为持有期内的资产损失；VaR为在置信水平C的情况下，资产在风险中的所拥有的价值。因此，从该式中我们不难看出，要计算VaR，需要三个条件，即：

确定一个适合的置信水平C；

分析清楚资产的收益分布情况；

确定一个合适的资产持有期。

现假定资产的收益率服从正态分布N(μ，σ2)，就可得到一般求解VaR的方差协方差模型，即：

其中，ω0为初期的资产；Δt为持有期。由于目前已有大量的实证表明，我国的证券股票收益率不是按照正态分布的，因此，研究人员采用了多种尖峰厚尾的分布来模拟计算VaR，如采用t分布，混合正态分布，GED分布和Laplace分布等。

1.2 CVaR的理论及特征

CVaR指的是损失超过VaR值的均值，亦称为期望损失。也就是说，对于、给定的vaR值，CVaR表示为损失大于该值条件下期望的损失，假设X表示为资产的损失，若其中X＞0，则资产出现损失，计算出的CVaR值，是大于VaR的一系列极端值的所取的平均值，则CVaR的可表达为：

由上式可得，CVaR实际上是相对于VaR的一个条件期望值。CVaR优于VaR，主要在于两点：

与VaR不同，CVaR表示的是一个尾部损失的期望值，而不是一个简单的分位点，因此，要计算CVaR，必须把所有大于VaR的损失值都考虑到，所有说CVaR能充分的度量对尾部的损失。其次，研究人员通过各种不同的方式证明CVaR是满足次可加性，即对于两个不同的资产A、B，式（4）总能得到满足：

由（4）式可看出，CVaR是一种一致性的风险统计量。另外，不难发现，CvaR是凸性的风险统计量，通过优化，可以找出基于CVaR投资组合存在的最小风险的解，而VaR并不是凸性的风险统计量，因此无法找到最优解。

2.3 VaR和CVaR的构建模型

全球风险管理协会定义风险值VaR为一个持有期内金融资产出现的最大损失，若我们预先设定一个值，则实际损失超过VaR的概率小于该设定的值。在确定的某个置信水平下和损益概率分布条件下，可用某个数字来表达整个分布情况，而损益水平x将不会超过这个值。VaR表示的是一个损失的值，通常取其绝对值，若分布是离散的话，则VaR就至少是使得右尾概率最小的损失值，可表达为：

由于VaR实际上只是个简单的数值，因此，VaR值测量方法虽然较为简单，但却忽视了可能存在的各种不同分布情况。为了得到精确的风险预测结果，研究人员采用条件VaR测量法，计算损失在高出VaR值这个条件下的平均值，即CVaR。

由于CVaR表达的是给定的置信水平下最大损失的期望值，故CVaR大于VaR。相对于VaR来说，CVaR对损益分布的度量更为准确，尤其是在影响损益分布的因素不对称时，CVaR能更精确全面的表达其分布特征。优化投资组合时，若CVaR降低了，则VaR亦会跟着降低，反之则不然。

在通过统计数据，并计算出VaR和CVaR值后，为验证其结果的准确性，需对其作出相应的检验，即进行后验测试，也就是在给定的置信水平C下，将实际的损失高于VaR值的比例P’与期望比例P进行对比，并得出一个失败率来评估VaR模型的优劣。

假设测量出现失败的天数为N，测量天数总计为M，则失败天数N与总计天数M的比值为p’=N/M，假设P’服从伯努利分布，即B～(M，P’)。则可进行如下检验：

原假设H：P=P’；备选假设：H1≠P’。对于原假设，本文采用似然比率检验法，其统计量可表达为：

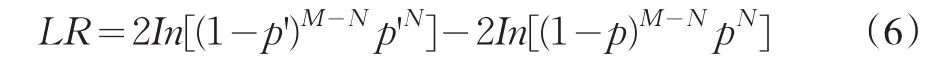
由（6）式可知，该统计量LR是服从χ2分布，其自由度为1，通过查表得知：

而对于CVaR值的检验，重点度量的是损失超过VaR的值与CVaR值之差的大小，先采用的目前较为常用的绝对额指标DLC，来表示二者平均数之差的绝对值，其检验如下：

其中X为大于VaR值的实际损失(X＞0表示亏损)，且DLC值越小，则模型效果越好。

2 VaR与CVaR模型对H股指数期货风险度量的实证

本文以H股股指期货收益为例，采用族模型其波动情况进行研究。

2.1 GARCH族模型

2.1.1 GARCH(p，q)模型

由于利率、汇率、金融资产等资产收益率的方差波动序列，通常都没有恒定的方差和均值，而是随时都在变化，有较为明显的集聚性，而资产持有者最看重的是持有期内收益的波动，因此，对风险进行预测和评估显得尤为重要。在模型中具体包括：

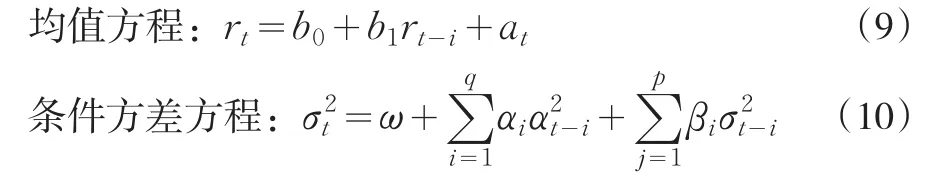
GARCH(1，1)中，p=1，q=1，即：

公式（9），（10），（11）中，对于GARCH(1，1)模型，α+β＜1。ω是常数项，rt是收益率，σt损失条件标准差，at是残差，αi与βj是各期参数，q和p分别是ARCH项和GARCH项最大的滞后阶数。

2.1.2 EGARCH(p，q)模型

在市场上，利好信息对波动性的影响远小于利空信息对其的冲击，这是资产价格的一个重要特征，而对于大多数股票来说，未来波动与当前收益之间有着较强的负相关性。为了在模型中体现出影响不对称的现象，提出了EGARCH模型，该模型不需要非负限制，其表达式为：

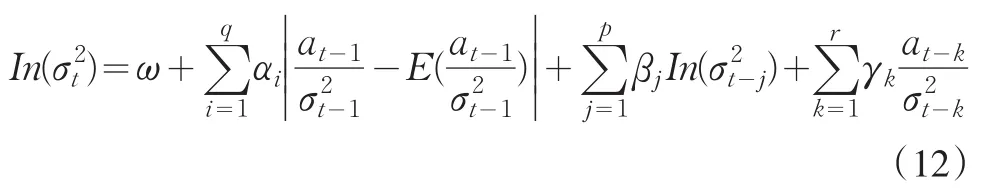
2.1.3 PARCH(p，q)模型

PARCH模型是一种标准离差的模型，它将残差的绝对值带入模型，其公式为：

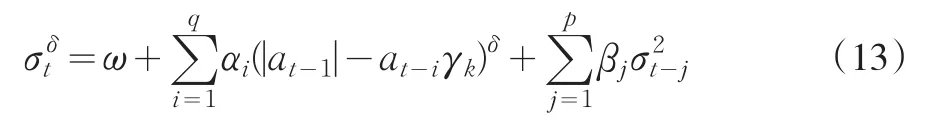
式中δ＞0；γ为非对称效应参数，若i＞r时，γi=0，r＜q；若i=1，2，L，r时，|γi|＜＜1。

2.2 计算不同的GARCH族模型残差分布下VaR和CVaR值

2.2.1 收益残差的分布假设

由于股票的收益率遭受重大获利或重大损失的概率较高，因此，不能单一的将其看做服从正态分布，故用广义误差分布和T分布和来反映更为合理，T分布概率密度函数如下：

2.2.2 不同收益残差分布下VaR和CVaR值的计算

本文利用参数法，计算VaR值如下：

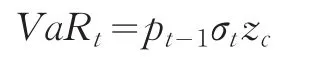
式中：pt-1表示资产的上一期所拥有的价值；σt表示利用GARCH族模型计算，得出的该期条件方差的标准差，；zc表示相应置信水平C下的分位数，取单尾，其取值受分布的影响；t表示资产的该持有期。

CVaR表示为条件的期望值，其计算式如下：

2.3 VaR与CVaR模型对H股指数期货风险度量的实证研究

2.3.1 检验正态性

通过H股指数期货的线性图，观察其日收益率可知：其收益率的波动通常无大幅波动，较为平缓。但是聚类现象有所体现，即收益率异常值出现的频率比较高，且集中出现在一个特定的时期。对H股指数期货日收益率进行正态检验，发现其有厚尾尖峰的特征，再加上其JB的统计量为，故不呈正态分布。

2.3.2 平稳性的检验

通过数据统计，得出在选定期间内，H股指期货收益率的ADF值为-36.5393，而当显著性水平取1%时，得Mackinnon的临界值仅为-2.232514，由于前者明显小于后者，故不采用单位根假设，即认为该段H股指期货的收益率序列为平稳的。另外，通过对其收益率进行自相关性检验，当检验到第七阶时，发现其自相关性较为明显，显著水平为0.061，在进一步尝试另外的滞后阶数后，得出收益率rt的均值方程用rt=b0+b1rt-7+at较为合理，其中at表示残差。

2.3.3 检验残差的自相关性和ARCH-LM

对均值方程进行拟和，并对残差及其平方进行自相关性检验，得出收益率残差at的自相关性并不显著，而残差平方的自相关性却较为显著。

其中以残差平方的波动呈现出的相关性最为明显，当出现一个较大的幅度波动后，通常都伴随着另一个较大幅度的波动，而在经历一个较小幅度的波动后，也同样会伴随着另一个较小幅度的波动，表现出较为明显的集簇性和时间可变性，因此，适合采用族模型来对H股指期货的收益率进行建模。另外，通过对残差at项的ARCH-LM继续检验，得出在LM和F统计量的显著水平处，都对无异方差的原假设拒绝，也就是说，残差中ARCH效应较为显著。更一步说明了用GARCH族模型建模较为适合。

2.4 利用参数估计计算VaR与CVaR值

2.4.1 残差服从正态分布

表1为三种模型的不同参数在残差服从正态分布情况下的估计值，在95%的置信水平下显著。用异方差效应检验各模型估计后的残差，其结果表明三个模型均无显著的异方差现象，说明该模型能较好的反映出股市对数收益率序列的异方差现象。

表1 各模型在正态分布下的参数估计

在正态假定下，取置信水平为95%时，利用公式VaRt=pt-1σtzc，计算得出表2。其中失败天数表示为实际损失高于VaR值的天数，而失败率为失败天数与总天数的比值,实际损失为△Pt=|Pt-Pt-1|，其中Pt表示H股股指期货日收盘价。

各个模型计算出的值的变异系数及返回失败率如下：

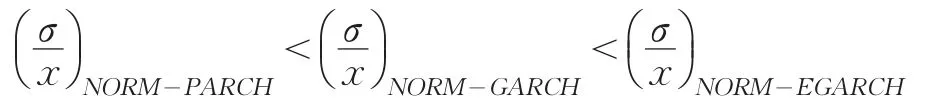
失败率NORM-EGARCH＜失败率NORM-PARCH＜失败率NORM-GARCH

由上面结果可以看出：三个模型估计相差不大，且失败率在5%左右，均小于3.841，其中以GARCH模型估计的失败率最大，PARCH模型居中，而EGARCH模型对VaR值估计偏高，故其失败率最小。由于在显著水平为95%，对LR统计量检验过程中，无法拒绝其零假设，故利用这三个模型计算出VaR值均较为准确。但根据综合变异系数的评价，EGARCH模型预测效果最差，GARCH模型预测效果其次，而PARCH模型预测效果最优。

表2 各模型在正态分布下VaR值和CVaR值的测量结果

另一方面，对于CVaR的计算结果：VaR的标准差与均值均小于CVaR，失败率也大于CVaR，由于CVaR值在置信水平为95%时下的条件分位数为2.0515648，大于分位数1.6984，再加上CVaR表示损失大于给定的VaR值条件下的期望损失，故由计算结果得出：

根据DLC统计量，在VaR估计失效时，CVaR值与均值比较接近，故对CVaR估计的损失仍较为准确的。表明CVaR值在正态分布下DLC统计量数值较小，对风险的估计效果较准确；另一方面，EGARCH模型也存在缺陷，该模型计算的CVaR值变异系数和估计的风险均较大，故可能会导致成本上升。

2.4.2 残差服从T分布

通过Eview5.0软件，得出的T分布的自由度参数d，并使用@qtdist(Zc，d)命令，可得出条件分位数和分位数如下：

表3 各模型在T分布下地估计参数

同样也可得出在T分布模型下VaR的估计值，取显著水平为95%，则三个模型的LR统计量均大于3.841，故拒绝零假设，即三个模型的估计效果都较差，相对而言，T分布下EGARCH模型的效果最差，GARCH模型的效果居中，PARCH模型的效果较好。具体为：

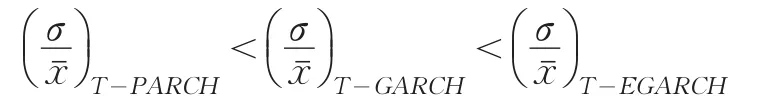
失败率T-EGARCH＜失败率T-PARCH＜失败率TGARCH

CVaR值在不同模型下的测量结果比较：

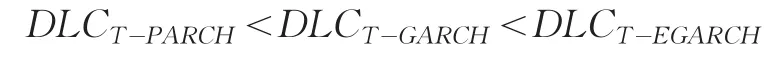
表4 T分布下各模型VaR值和CVaR值的测量结果

2.4.3 残差服从GED分布

利用软件Mathematica，得出GED分布下的估计结果，见表5：

表5 GED分布下各模型内参数的估计结果

表6 GED分布下各模型VaR值和CVaR值的测量结果

由表6可知：

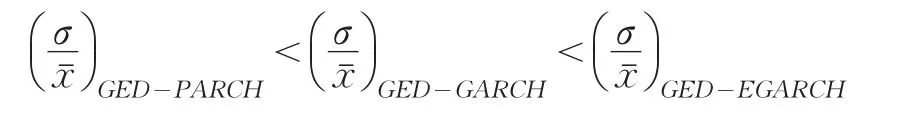
失败率GED-PARCH＜失败率GED-EGARCH＜失败率GED-GARCH

在显著水平为95%时，经过综合比较，虽然各模型的LR统计量都能通过返回检验，但效果还是有一定的差别，其中EGARCH模型的VaR值波动较大，故效果较差，GARCH模型的效果居中，PARCH模型失败率较低，效果最为稳定。

三个模型计算得CVaR值结果比较如下：

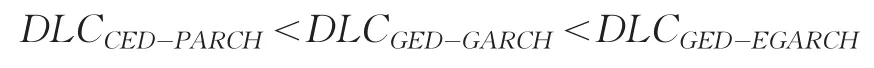
利用PARCH模型得出的CVaR值，在T分布与正态分布下得出的DLC值明显大于CED分布下的DLC返回检验值，故PARCH模型更适合估计GED分布。

3 结束语

本文分别在正态分布、T分布、GED分布下，利用GARCH族模型分别对H股指数期货收益率各日的VaR值进行计算，结果表明：在T分布下，三种模型均未通过检验；但在正态分布和GED分布下，三种模型的测量结果均通过了检验。本文进一步利用GARCH族模型分别在三种分布下计算CVaR值，其结果表明：在VaR值效果欠佳的时候，使用CVaR值仍然能够比较准确的度量这些极端损失，对CVaR值的测量效果最佳的是基于GED分布的PARCH模型。

综上，基于GED分布的PARCH模型在计算VaR与CVaR值都是最优的。希望这个结论对预测未来我国沪深300股指期货受益波动风险方面有所帮助。

[1]Benati,Luca,Surico,Paolo.VAR Analysis and the Great Moderation[J].The American Economic Re⁃view,2009,99(4).

[2]R.Tyrrell Rockafellar,Stanislav Uryasev.Condition⁃al Value-at-risk for General loss Distribution[J].JournalofBanking&Finance,2002,(26).

[3]DU Wei,Wahg Hong-li.EaR-Based Research on CreditRisk[J].Journalof Yangtze University(Nat⁃uralScienceEdition)Sci&Eng.,2008,(1).

[4]Tinga C,Warachka M,Zhao Y.Optimal Liquidation Strategiesand Their Implications[J].Journal of Eco⁃nomic Dynamics&Con tro,2007,(31).

[5]吕宝林，张凤香.股指期货风险及其防范[J].中国管理信息化,2010,（3）.