空气污染潜势-统计结合预报模型的建立及应用

黄晓娴,王体健,江 飞 (南京大学大气科学学院,江苏 南京 210093)

目前,空气质量日益受到人们的关注.全国各地已纷纷开展空气质量的预报工作[1-4].空气污染预报分为潜势预报和浓度预报.前者是在污染源一定的条件下,以天气形势及其气象要素指标为依据,对未来大气环境质量状况进行定性或半定量的预报.后者主要预报污染物浓度、空气污染指数或空气质量等级,从方法上又分为数值预报和统计预报.数值预报为利用数学方法和计算技术,以大气污染扩散的物理化学机制为基础,计算一定区域内空气污染物的浓度.统计预报是利用统计方法建立气象因子与空气质量之间的关系.国内外许多学者对城市及区域的空气污染过程的特征及预报开展了大量的研究,取得了不少成果.用于城市或区域空气质量预报的数值模式有WRF/Chem,MM5/CMAQ,RegAEMS等[5],对初始场的处理有三维同化等方法[6].数值模式的优点在于可以进行不同时空尺度上高分辨率的计算,缺点在于计算量大,耗时长.统计预报需要大量历史污染监测资料和气象观测资料,统计方法有回归法,CART 法[7-8],神经网络法[9],等等.统计预报的优点在于简单易行,因此应用较为广泛.潜势预报的特点在于避开了具有不确定性的污染源,重点关注影响空气质量的气象因子,包括地面天气形势,各气象要素[10-11].其中,较小的风场,稳定的大气条件等因素是造成空气污染的必要条件[12-13].

南京位于长江下游沿岸宁镇丘陵区,是长三角地区承东启西的重要城市.南京即将举办 2014年青奥会,空气质量问题受到高度重视.Deng等[14]对南京能见度特征分析发现,天气形势对空气污染和能见度有重要影响.芮冬梅等[15]对南京市环境空气质量与气象条件的关系分析发现,NO2与PM10受城市机动车尾气的影响较大.王学远等[16]利用数值模式模拟了南京典型天气条件造成的污染过程,发现重污染发生在长时间逆温条件下,同时地形也是主城区重污染的影响因子之一.

本文在前人研究工作的基础上,考虑了影响空气污染的气象因子和大气扩散清除因子,构建空气污染潜势指数 APPI(Air Pollution Potential Index),并利用南京地区 2009～2010年实测资料计算APPI,拟合空气污染指数API与APPI的关系,建立了一个空气污染潜势与统计相结合的预报模型.利用中尺度模式 WRF预报的气象场,针对2011年1～12月开展实况预报,同时利用实际观测的气象场进行回顾预报,检验模式性能.

1 资料来源与处理

2009年1月～2011年12月南京逐日空气污染指数资料来自南京市环境保护局.同步逐时气象资料及每日08:00及20:00探空资料来自位于32.00°N,118.80°E 的观测站点.逐日各时次天气图来自江苏省气象信息共享平台网站.火点资料来自环境保护部的生态监察资料.重大沙尘天气参考气象台沙尘预警信息和全国各地新闻报道.

由于本文所采取的预报方法中并不考虑污染源的变化,故将受外来源影响的数据剔除.可能受到外来源影响的时间段主要为:燃放鞭炮的春节期间、沙尘暴频发的春季、燃烧秸秆的初夏和秋季等等.

本预报模型需要气象场作为输入,采用的是WRF模式的预报结果.WRF是美国国家大气研究中心(NCAR)、美国国家大气海洋总署-预报系统实验室、国家环境预报中心(FSL,NCEP/NOAA)等多个机构共同发展的新一代中尺度数值模式.它采用了高度模块化、并行化和分层设计技术,集成了迄今为止在中尺度方面的研究成果,适合1～10km 内高分辨率的预报及模拟研究.本文采用了3.0版本的WRF,模式区域采用Lambert投影,设置了 4 层嵌套,区域以南京(32.0°N,118.8°E)为中心,最大区域(DM1)覆盖了整个东亚地区(包括了中国,中南半岛,朝鲜半岛及日本等地区),格距为81 km;最内层区域覆盖了南京市,格距为3 km.垂直使用 σ坐标,从地面到100hPa共分为24个 σ层.采用 WSM5云微物理参数化方案,Grell-Devenyi积云对流方案,Mellor-Yamada-Janjic边界层参数化方案,NOAH陆面模式,并且在模式最内层区域启用了单层的城市冠层模式UCM.

2 潜势-统计预报模型

2.1 空气污染影响因子的确定

2.1.1 风 在水平方向上,风对污染物起到输送和稀释的作用.风速越大,输送和稀释作用就越强.故引入地面风速、混合层内平均风速等因子.

风向的集中程度也影响污染物的输送与稀释.风向集中程度越高,对污染物的输送与稀释效果越显著.引入风向日变化因子,采取如下风向矢量计算方式:

将每小时风向 θi按三角函数矢量分解为 x方向和y方向,

取风向在 x方向和 y方向上分量的日平均值,

计算风向在x方向和y方向上分量的标准差的矢量和的模Θ,即为风向日变化因子.

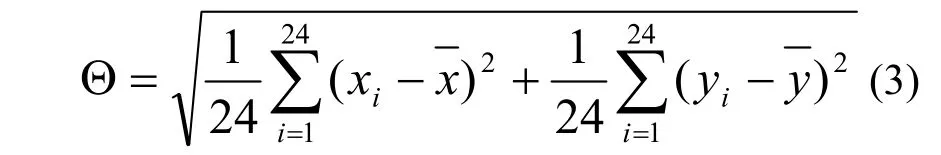
2.1.2 混合层 混合层是大气边界层内气象要素随高度分布趋于均匀的层次.混合层内,位温、湿度、风速风向等物理量随高度变化很小.混合层越高,越有利于污染物的扩散稀释.引入混合层高度因子,计算方案参考文献[17].

2.1.3 大气稳定度 大气层结的稳定程度影响湍流的活动,这里用M-O长度L来确定稳定度级别,如表1所示.

表1 由M-O长度L判定稳定度级数Table 1 Stability levels determined by Monin-Obukhov length L

2.1.4 扩散系数 扩散系数是表征湍流输送能力的量.引入近地面层内的垂直扩散系数因子,在近地面层中( Z≤Zs,ZS是近地面层高度),根据Businger[24]的相似理论,有:

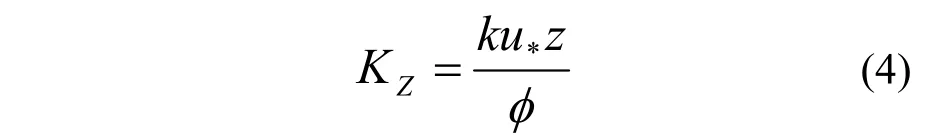
式中: k是Von Karman常数; u*是摩擦速度;廓线函数φ根据Businger[24]和Carl[25]分别给出的形式为:

式中:L是M-O长度.

2.1.5 干沉降 干沉降过程是污染物从大气中清除的重要途径之一.这里引入 SO2干沉降速率,NO2干沉降速率,PM10干沉降速率等因子,计算方法参考文献[18].

2.1.6 湿清除 湿清除是污染物主要的汇之一.由于降水过程的时效性及清除效果的滞后性,故同时考虑当天和前一天的降水时长.以h0代表当天降水小时数,h-1代表前一天降水小时数.一般而言,降水持续时间越长,湿清除效果越显著.采取复合分档法,如表2所示.

表2 降水时长分档情况Table2 Grades of precipitation duration

2.1.7 地面天气形势 天气形势或大尺度天气系统的移动路径,直接影响各气象要素的变化.由于天气形势类型繁多复杂,所以采取如下变压和风向结合的方式将每天的地面天气形势进行分类:

①24h变压Δp的分类.考虑前一天的24h变压Δp-1和当天的24h变压Δp0,将其分为6类,如表3所示.若连续2d的变压情况不一致,说明受到该天气系统影响时间短.若连续2d的变压情况一致,说明受该天气系统影响强烈.升压代表高压系统迫近或低压系统远离,连续升压代表高压系统 持续迫近,同理可得平压、降压的情况.

表3 变压情况分类Table 3 Allobaric classification

②风向的划分.考虑一天24h次风向的分布.根据风向和风速将其分为9个象限.将风速大于0.5m/s的风分为北、东北、东、东南、南、西南、西、西北8个象限,将风速小于等于0.5m/s的风划分到静风象限,为第9象限.

每天的主导风向结合变压情况可以反映当天的天气系统相对于城市的位置及移动状态.以南京为例,升压配合西北风或北风为高压前,升压配合东北风为高压底,降压配合东南风为高压后等等,依次类推.

统计南京各种天气形势下的平均 API并将其分档:50～65为1,65～75为2,75～85为3,85～95为4,95～110为5,110以上为6.整理结果见表4.

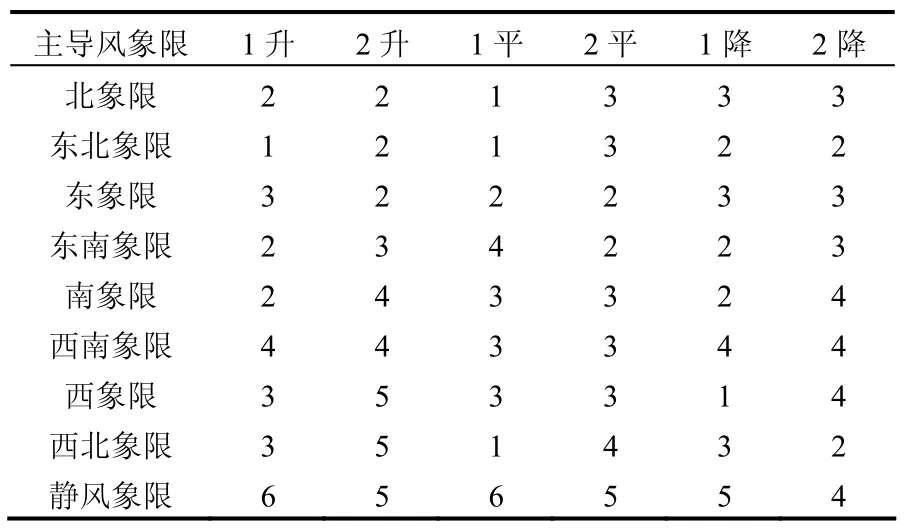
表4 各地面天气形势下的平均API的分档整理Table 4 Classification of average API in different synoptic systems

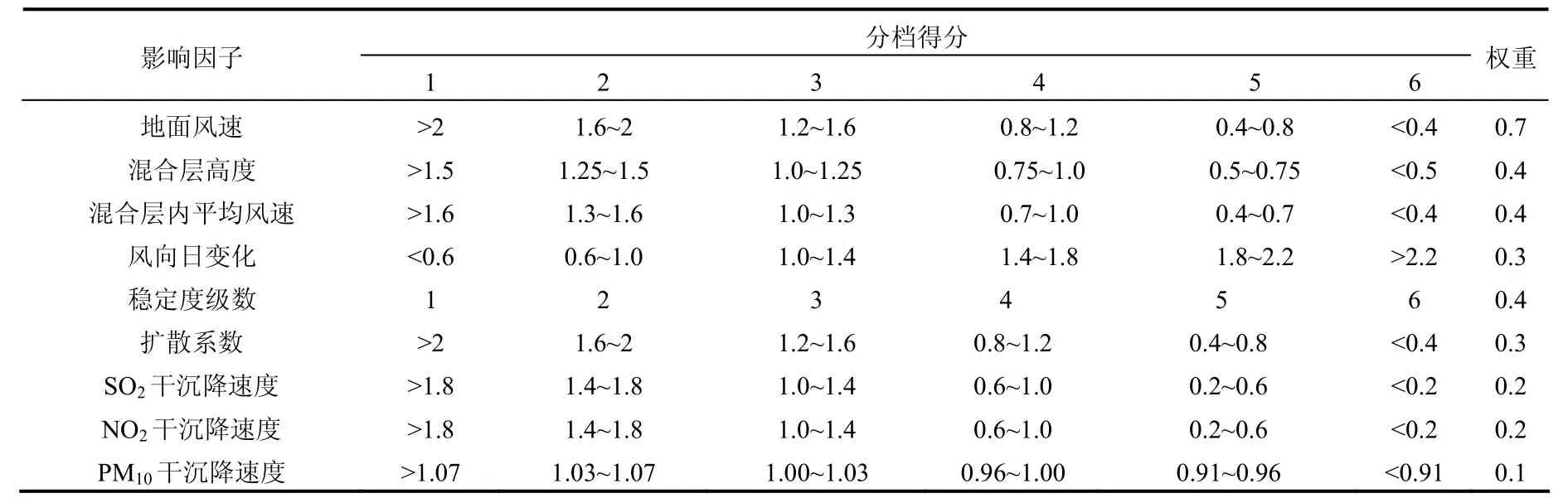
表5 影响因子的分档及权重系数Table 5 Grades and weights of factors

2.2 空气污染潜势指数的构建

将2.1节中各因子划档分级.共有地面风速、混合层内平均风速、风向日变化、混合层高度、稳定度级数、扩散系数、SO2干沉降速率、NO2干沉降速率、PM10干沉降速率、降水时长、地面天气形势11个因子.除风向日变化、降水时长、地面天气形势3个因子,其他因子作日平均.其中,稳定度级数按表1分档,降水时长因子表2分档,地面天气形势因子按表4分档.其他8个因子,先进行归一化处理,即各因子除以各自的平均值.然后从低到高分为6档,档位越高,对应越具有发生空气污染的趋势.进一步根据各因子的重要性赋予不同的权重,分档情况及权重系数如表5所示.最后利用式(6)计算每天的空气污染潜势指数APPI:

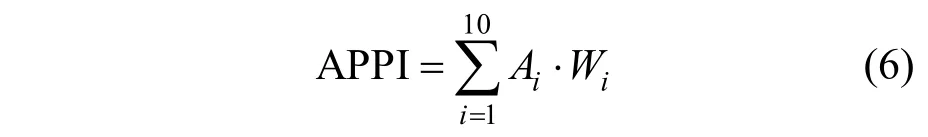
式中:Ai代表第i个影响因子的分档得分;Wi代表第i个影响因子的权重系数.

2.3 空气污染指数的计算

基于统计方法建立空气污染指数 API与空气污染潜势指数 APPI之间的函数关系,以此实现利用APPI进行API的预报,即:

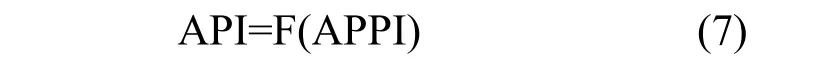
3 案例应用

3.1 拟合函数的构建

基于南京地区2009～2010年资料,利用上述潜势-统计预报模型计算逐日 APPI,采用指数函数、二项式函数、三项式函数分别拟合,得到拟合 API与实际 API的相关系数分别为0.6587、0.6682、0.6689,拟合API的等级准确率如表6所示.

表 6 各拟合函数所得 API的等级准确率(优秀:API≤50,良好:50＜API≤100,污染:API＞100)Table 6 Level accuracies of different fitting functions (Good: API≤50, Moderate: 50＜API≤100, Unhealthy: API＞100)

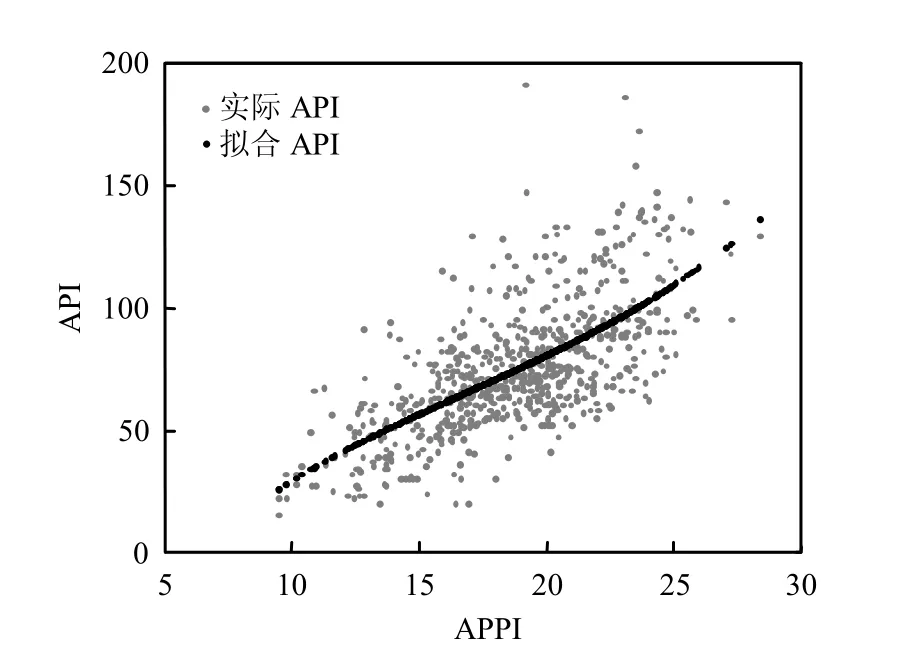
图1 2009～2010年APPI与API的关系Fig.1 Relationship between APPI and API during 2009～2010

由表6可见,三者对于优秀和污染等级均为漏报次数多于空报次数.对于优秀等级,指数函数空报的最少,但是漏报的最多,报对的次数也最少,而二项式函数略优于三项式函数.对于污染等级,二项式函数与三项式函数预报相差不大.总体而言,二项式函数和三项式函数的正确率接近,且略优于指数函数,故选取三项式函数为拟合函数F:

确定各项系数为a3=0.0111,a2=-0.5645,a1= 14.3054,a0=-68.4266.拟合结果如图1所示.

3.2 实况预报

基于API和APPI的统计关系,针对南京地区2011年1～12月,利用WRF预报的24h气象场、48h气象场和观测的气象场分别开展空气质量实况预报和回顾预报,并与实际情况比较,结果如图 2所示. 逐月预报等级正确率如图 3所示.

总体而言,本文所建立的潜势-统计预报系统基本能够预报南京逐日空气质量变化的趋势.24h预报与 48h预报的年均等级正确率为60.6%和62.4%.实况预报等级正确率逐月差异较大,1月预报情况最好,24h预报和48h预报等级正确率分别达到87.5%和100%.实况预报在4月偏低较多, 24h预报和48h预报等级正确率分别为44.4%和46.4%.回顾预报等级正确率逐月差异不大,为63.0%～80.0%之间,年均等级正确率为73.1%.

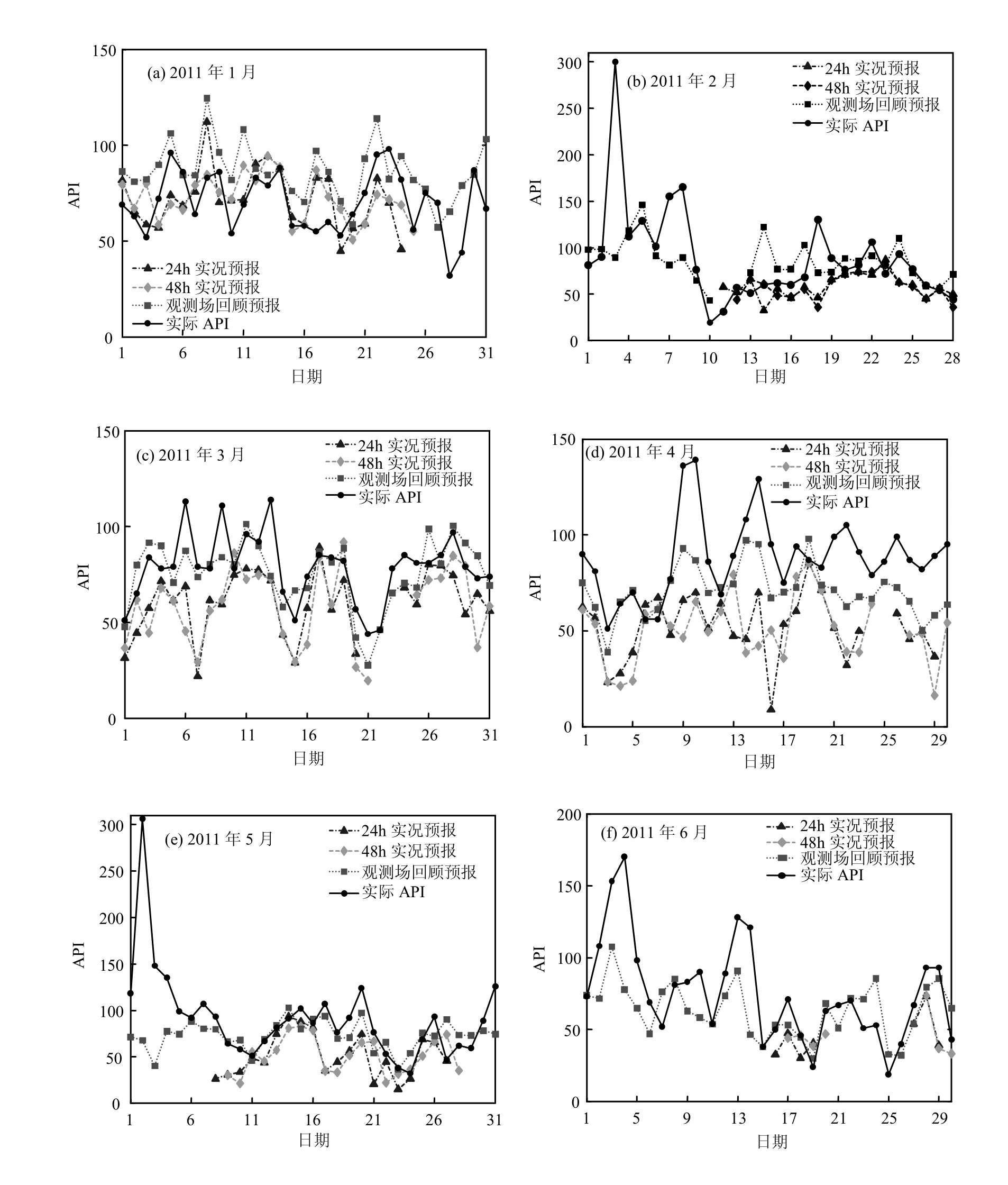
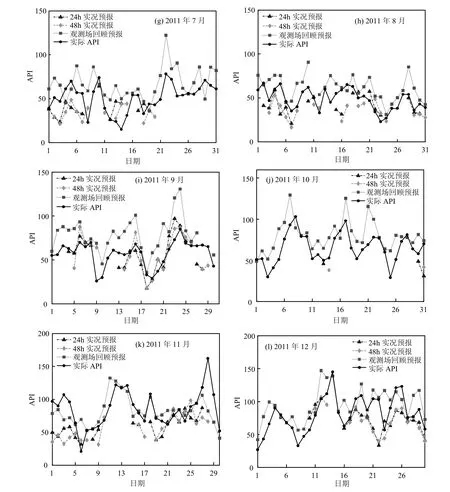
图2 预报API与实际API的比对Fig.2 Comparison of forecasting API and actual API

若定义预报API与实际 API的值相差±x(x为误差的绝对值)以内为正确,则进一步统计2011年预报的API正确率,结果如图4所示.单独统计相差±20以内逐月API正确率,如图5所示.

图4可见,当预报API与实际API的差值的绝对值x加大时(即认为API正确的标准更宽泛),预报的API正确率增加.回顾预报的正确率始终高于实况预报.在x＜13, 24h预报的正确率高于48h预报;在x=20, 24h预报、48h预报、回顾预报的年均正确率分别为58.1%, 59.4%和63.8%,在8、9月24h预报、48h预报正确率达到80%以上,最高达85.0%,在3月回顾预报正确率达90.3%.

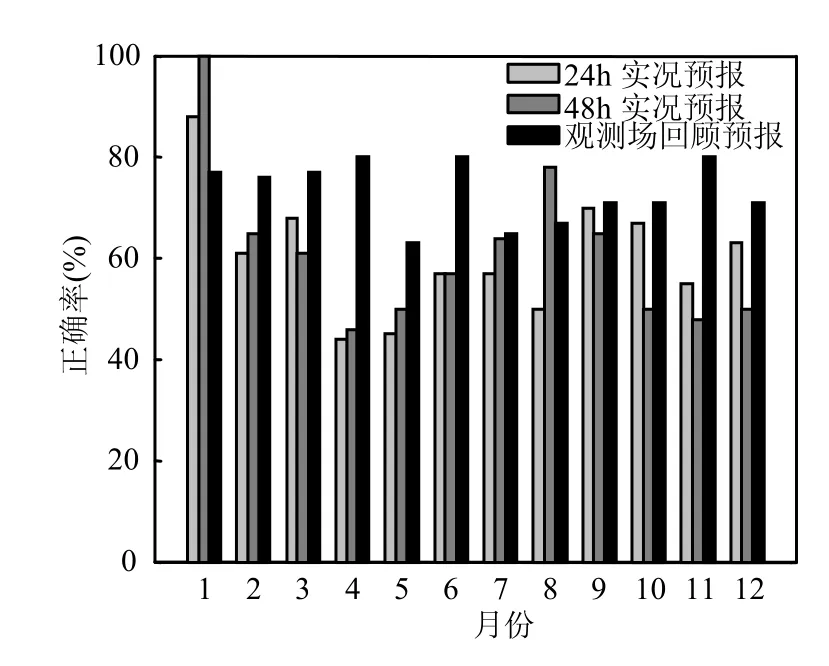
图3 逐月预报空气质量等级正确率Fig.3 Monthly accuracy rate for air quality level forecast

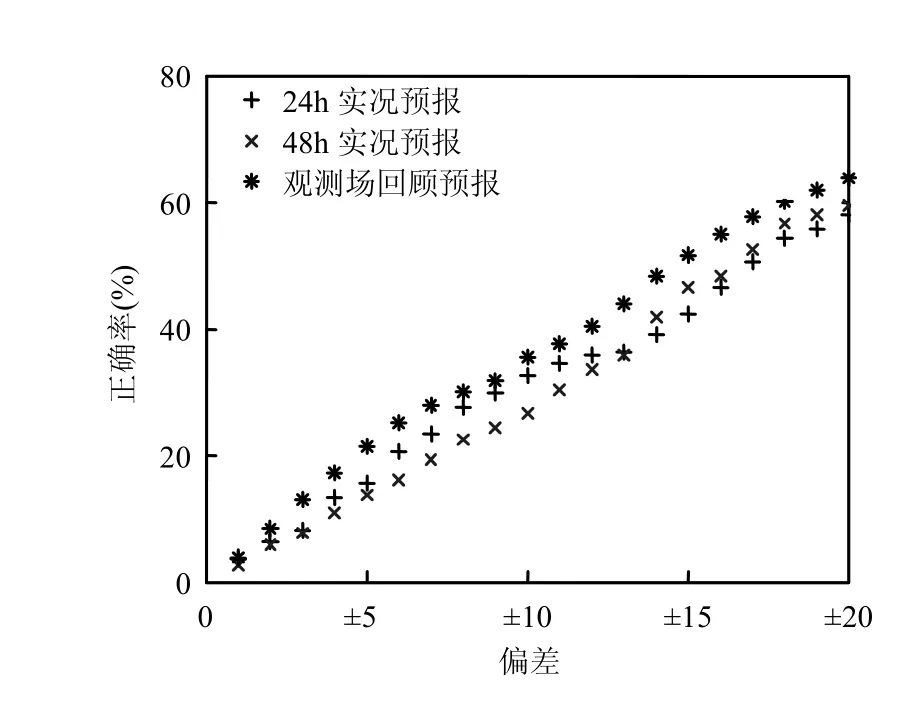
图4 API正确率随误差的变化Fig.4 Variation of API accuracy rate with difference

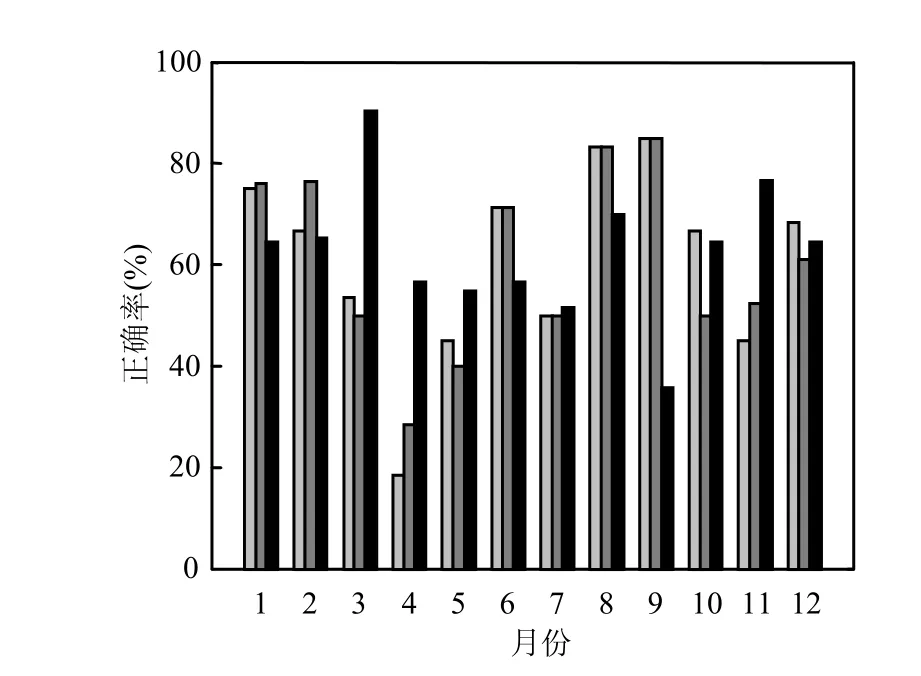
图5 预报API与实际API相差±20条件下的逐月正确率Fig.5 Monthly accuracy rate for difference of forecasting and actual API within ±20

4 讨论

本文建立的潜势与统计结合的空气质量预报方法可以实现对API的定量预报,在实际应用当中需要注意以下问题:

(1) 该方法为单点模型,即将应用城市视为一个点.因此,资料的选取对该方案的建立与验证均有一定的影响,其中风与降水的影响尤为突出,应选取具有代表性的气象站点和环境监测站点.

(2) 本方案是潜势与统计结合的预报模式,在模式建立之初,即假设源不变、只考虑潜在的天气形势变化对空气污染的影响.故在实际应用中并不能完全体现外来源的贡献.

(3) 由于近2年南京的首要污染物以可吸入颗粒物为主,因此,该方法所得权重因子更适合于PM10的潜势预报,实际应用中可分别针对PM2.5、O3、SO2、NO2建立相应的预报模型.

5 结论

5.1 作为一种空气污染潜势与统计结合的预报方法,该模型不仅考虑了气象因子,还考虑了大气扩散清除因子;不仅可以给出空气污染潜势,还可以给出空气污染指数.

5.2 统计预报等级正确率:24h预报为44.4%～87.5%,平均为60.6%;48h预报为46.4%～100%,平均为62.4%;回顾预报为63.0%～80.0%,平均为73.1%.

5.3 若定义预报API与实际API的值相差±x(x为偏差的绝对值)以内为正确,当x=20时, 24h预报、48h预报和回顾预报的年均正确率分别为58.1%, 59.4%和63.8%.

5.4 该模型计算效率很高,在IBM x3500并行集群服务器上计算, 48h预报需要机时3h.

[1]王迎春,孟燕军,赵习方.北京市空气污染业务预报方法 [J]. 气象科技, 2001,4:42-46.

[2]孙 峰.北京市空气质量动态统计预报系统 [J]. 环境科学研究, 2004,17(1):70-73.

[3]王建华,于 鹏,郭素荣.青岛市空气污染统计预报方法研究 [J].青岛大学学报, 1999,14(4):60-62.

[4]韩志伟,杜世勇,雷孝恩,等.城市空气污染数值预报模式系统及其应用 [J]. 中国环境科学, 2002,23(3):202-206.

[5]Wang T J, Jiang F, Deng J J, et al. Urban air quality and regional haze weather forecast for Yangtze River Delta region [J]. Atmos.Environ., 2012,58:70-83.

[6]Liu Z Q, Liu Q H, Lin H C, et al. Three-dimensional variational assimilation of MODIS aerosol optical depth: Implementation and application to a dust storm over East Asia [J]. J. Geophys. Res.,2011,116,D23206,doi:10.1029/2011JD016159.

[7]Burrows W R, Benjamin M, Beauchamp S et al. CART decision-tree statistical analysis and prediction of summer season maximum surface ozone for the Vancouver, Montreal, and Atlantic Regions of Canada [J]. J. App1. Meteor., 1995,34(8):1848-1862.

[8]杨元琴,王继志,侯 青,等.北京夏季空气质量的气象指数预报[J]. 应用气象学报, 2009,20(6):649-655.

[9]白晓平,张启明,方 栋,等.人工神经网络在苏州空气污染预报中的应用 [J]. 科学导报, 2007,25(3):45-49.

[10]张 蕾,江 崟.深圳地区空气污染潜势预报的研究 [J]. 广东气象, 2001.1:1-3.

[11]张国琏,甄新蓉,谈建国,等.影响上海市空气质量的地面天气类型及气象要素分析 [J]. 热带气象学报, 2010,26(1):124-128.

[12]王 宏,冯宏芳,隋 平.福州市空气高污染与气象条件关系 [J].气象科技, 2009,37(6):676-681.

[13]王喜全,虞 统,孙 峰,等.北京 PM10重污染预警预报关键因子研究 [J]. 气候与环境研究, 2006,11(4):470-476.

[14]Deng J J, Wang T J, Jiang Z Q, et al. Characterization of visibility and its affecting factors over Nanjing, China [J]. Atmos. Res.,2011,101:681-691.

[15]芮冬梅,张予燕.南京市环境空气质量与气象条件的关系分析[J]. 环境科学导刊, 2009,2(2):37-38.

[16]王学远,蒋维楣,刘红年,等.南京市重点工业源对城市空气质量影响的数值模拟 [J]. 环境科学研究, 2007,20(3):33-43.

[17]王体健,孙照渤,李宗恺,等.中国法规大气扩散模式及其与其他模式的比较 [J]. 环境科学研究, 1998,11(6):9-12.

[18]张 艳,王体健,胡正义,等.典型大气污染物在不同下垫面上干沉积速率的动态变化及空间分布 [J]. 气候与环境研究, 2004,9(4):591-604.

[19]沈 毅,王体健,韩 永,等.南京近郊主要大气污染物的观测分析研究 [J]. 南京大学学报(自然科学), 2009,45(6):746-756.

[20]史慧敏,沈觉成.南京北郊低空污染气象条件若干特征 [J]. 地理研究, 1992,11(2):60-67.

[21]苏福庆,杨明珍,钟继红,等.华北地区天气型对区域大气污染的影响 [J]. 环境科学研究, 2004,17(3):16-20.

[22]王喜全,王自发,虞 统,等.西太平洋热带气旋路径对北京 PM10污染的预示作用 [J]. 科学通报, 2009,54(1):93-97.

[23]李 琼,李福娇,叶燕翔,等.珠江三角洲地区天气类型与污染潜势及污染浓度的关系 [J]. 热带气象学报, 1999,15(4):363-369.

[24]Businger J A, Wyngaard J C, Izumi Y, et al. Flux-profile relationship in the atmospheric surface layer [J]. J. Atmos. Sci.,1971,28:181-189.

[25]Carl D M, Tarbell T C, Panofsky H A. Profiles of wind and temperature from towers over homogeneous terrain [J]. J. Atmos.Sci., 1973,30:788-794.