最优插值法在对中国自动站降水量空间分析中的参数优化

沈 艳, 潘 ,徐 宾, 宇婧婧

(国家气象信息中心,北京100081)

0 引言

中国已建成自动气象观测站(包括国家级自动站和区域自动站)约32000多个,这些资料对于气象灾害预警、决策服务、数值预报模式评估和精度检验等具有重要意义。但受目前资料交换政策的限制,用户无法获得自动站观测的小时数据,因此如何将该数据快速、准确地转换成可供决策服务部门和广大科研用户使用的高质量产品,是综合提高气象防灾减灾能力、服务能力和科研水平的有效途径。

利用特定的空间分析方法,已有一些研究提出了适宜于日、侯或月时间尺度的降水量空间插值方法[1-10]。chen等[9-11]比较了Cressman、Shepard和最优插值(Optimal Interpolation,OI)3种方法插值逐日降水量时的精度表明:与只考虑距离权重的Cressman或Shepard插值不同,OI方法应用到空间内插时,除了距离还要考虑格点与站点以及站点与站点之间的空间相关性,其插值结果优于Cressman和Shepard两种方法。近年来,OI方法也应用到了小时降水量的空间内插中,如李春晖等[12]利用自动观测站数据,在中国站点分布相对均匀的广东省和广西省,进行了区域小时降水量的插值试验,认为降水比率OI方法为最优。作者同时指出,为了进一步提高小时降水量的空间插值精度,需要对核心参数进行优化。实际上中国自动站的分布非常不均衡,“东密西疏”的站网布局非常明显,约90%的自动站都建在了中国东部区域。在站点稠密区与某台站距离最近的台站间平均距离不到20km,但在站点稀疏区能达到100km以上。因此,针对现有的自动站站网布局,合理优化插值参数,对于提高中国小时降水量空间插值场精度是必要的。将中国分成3个区域,确定了OI插值中数据信噪比、相关随距离的函数关系。讨论影响台站数和初估场对小时降水量精度地影响。

1 数据和方法

1.1 中国自动站小时观测降水量

截止到2010年10月,中国已建成32742个自动观测站,站点的空间分布图见图1。可见,自动站在中国的分布极不均匀,约80%的站点分布在中国东南沿海地区,而青藏高原等地形复杂区的站点非常稀疏。为此,以40°N和100°E将中国分成3个区域(图1),分别对应中国站点较为稀疏的新疆北部、内蒙古大部和东三省(简称1区)、站点较为稠密的中国东部区域(简称2区)和青藏高原区域(简称3区)。自动站观测资料已实现了实时上传,针对降水量的质量控制方案也已于2009年7月实现了业务化[13],方案充分考虑了气候学界限值、区域界限值、时间一致性、空间一致性等检查,显著提高了降水资料的可靠性。选取了2010年7月经质量控制后的自动站小时观测降水量数据并将其格点化到0.1°×0.1°网格点上。

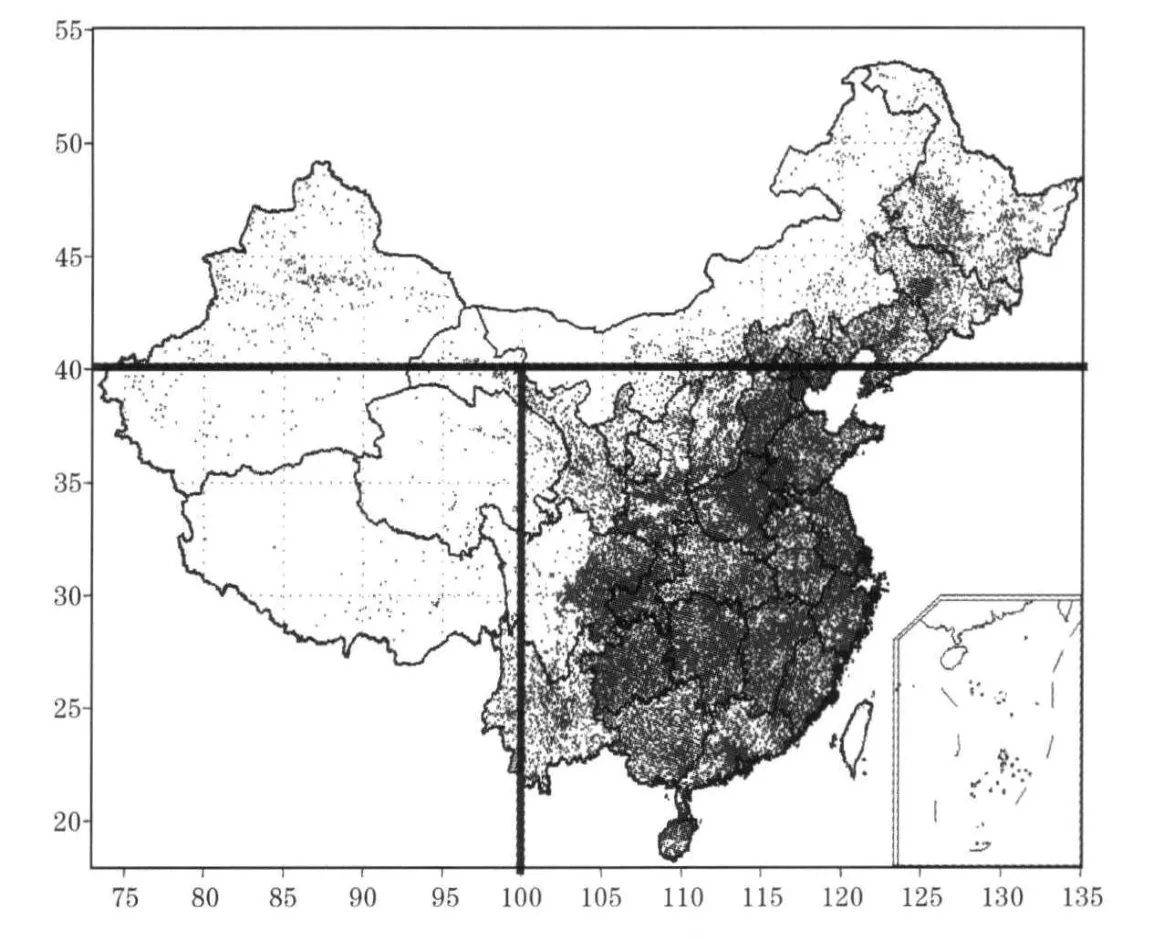
图1 中国自动站的分布及其区域划分

1.2 方法

Cressman、站点算术平均法、Shepard、Kriging等空间插值方法均是气象上常用的空间分析方法。但Xie et al.[14]、沈艳等[15]、李春晖等表明:考虑降水比率的OI方法在降水量空间插值时具有优势。

1.2.1 降水比率OI插值方法

降水空间变率大导致直接对其插值的误差也相对较大。因此,通常的插值思路是:先构建一个初估场,进一步借助初估场来定义一个新的要素,如降水量的差值[9]或比值[14]进行空间插值,以减小因降水量空间分布不连续而带来的插值误差。Xie等的研究表明:定义比值能获得更高的插值精度[14]。因而,针对小时降水的空间插值中也采用了通过初估场定义小时降水量比值的插值思路[12,15]。

1.2.2 精度评估方法

站点观测数据是最能“真实”反映观测点的数据源,因此在评估OI核心参数精度时,采用交叉检验方法,将站点数随机分成10等份,利用90%的站点值反插到另外10%的台站位置上,如此循环10次,使每一个台站都有一个实测值和一个内插值,然后利用平均偏差、均方根误差和相关系数等指标来定量评估调整OI方法中核心参数时的效果。

图2 不同分区在ee取不同值时对应的均方根误差

1.3 OI方法参数设置

1.3.1 观测误差标准差和初估场误差标准差的比率ee

这是OI方法中非常重要的参数之一,表示观测数据误差与初估场误差的比率,可近似认为是数据的信噪比。其中观测数据误差一是来源于观测误差,但通常认为站点观测数据的误差可近似忽略,另外一个误差来源是空间代表性误差。而初估场误差是时空分辨率和降水量的函数,一般很难被量化[14]。因此在3个分区中,通过人为变换不同的ee值(从0.01变换到1.5),并将误差最小时对应的ee值作为最优的观测误差标准差和初估场误差标准差的比率。3个分区中,ee取不同值时对应的均方根误差见图2,可见:不同区域下,ee取不同值时均方根误差的变化趋势比较一致,即随着ee增大,各区域的均方根误差均有小幅减小,之后随着ee的增大,均方根误差基本保持不变。各区域对应的均方根误差均在ee=0.3时达到最小,因此,在针对自动站小时观测降水量空间插值时,比率确定为0.3。

1.3.2 相关随距离的衰减关系

利用OI方法进行数据融合或同化时,需要确定两点之间误差相关与距离的定量函数关系式。站点资料空间分析时,一般认为站点观测不存在误差,或者认为这种误差可以忽略不计,因此可以简化成是两点间降水量时间相关系数与两点间距离的关系式。选取2010年7月份逐时降水观测资料(744个时次),分别计算了3个分区任意两点间降水量相关系数与距离。进一步按照距离大小分成多个等份,计算每个等份内所有样本的平均相关系数,图3显示了3个分区降水量相关系数与距离之间的关系及函数拟和式。可见3个分区中两点间降水量相关系数均随距离增加而减小,均可近似表达成随距离增加而呈e指数递减的关系,且3个区的拟和关系式基本一致。因此,在中国范围可近似用下式来表达相关随距离的衰减关系,即:

Cor=0.3*exp(-d/10.0)

其中Cor为两点间降水量的时间相关系数,d表示两点间的距离。

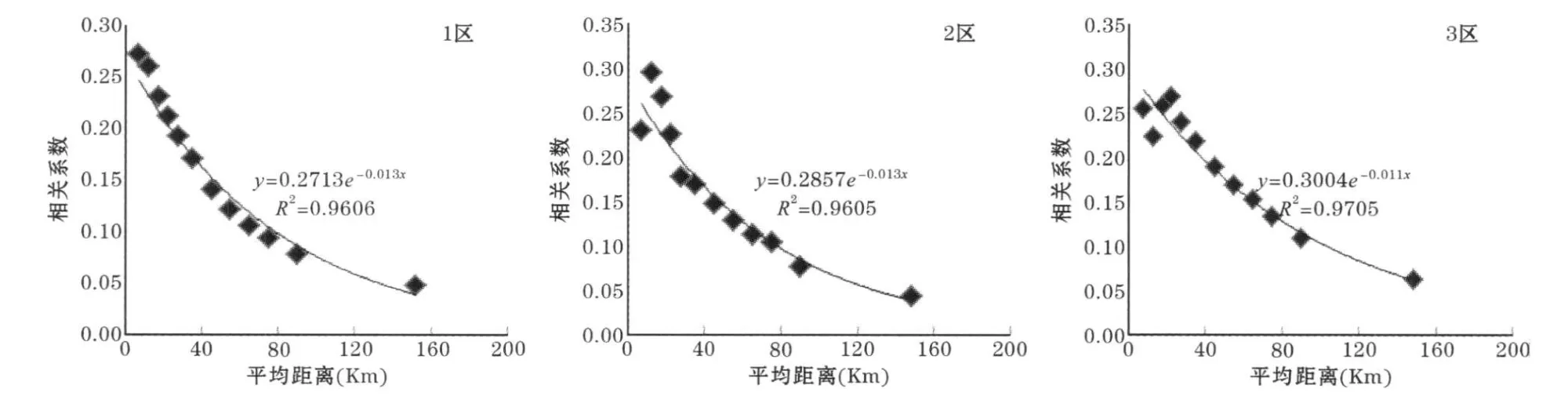
图3 不同分区两点间降水量相关系数与距离之间的关系

1.3.3 影响台站数和平均搜索距离

与只用距离作为权重的空间插值方法不同,OI方法在考虑搜索半径的同时还要考虑搜索半径内台站个数的影响,而且影响台站数的判断条件优先于搜索半径。选取2010年7月1日00时～2010年7月10日23时的逐时观测资料,当影响台站数从1变化到15时,逐时次交叉检验计算均方根误差(rmse)和平均搜索距离在3个区域的变化如图4,可见3个区域的插值误差均随着影响台站个数的增加而减小,之后维持着相对稳定的误差水平。对于1区,当影响台站个数达到4个及以上时,rmse就相对稳定,而对于2区和3区,该数值分别是5个和7个。因此,在针对逐小时降水量的OI插值方案中,影响台站数应至少在4个以上,以5～7个之间为宜。

图4 研究区均方根误差和平均搜索距离随影响台站个数的交叉检验结果

1.3.4 初估场

OI方法中需要提前建立初估场,在针对逐日、逐月站点数据的空间分析中,将日或月的气候标准值数据作为了初估场[11,14-15]。但由于小时降水的时空变率大,建立稳定可靠的小时降水量背景场需要更多的气象台站观测资料,而现有的资料质量和密度尚无法建立该初估场。因此在针对小时降水量的空间分析中仍采用了逐日降水量气候标准值作为初估场[12]。设计了3种初估场方案,即(1)NOAA气候预测中心(CPC)研制的考虑地形海拔高度影响的逐日降水量背景场[14];(2)国家气象信息中心制作的综合考虑了海拔、坡度、坡向与风向夹角的逐日降水量背景场[16];(3)用Shepard空间插值法[3]插值生成同时刻的降水分析场。采用3种初估场的交叉检验结果见表1。由于生成初估场1和初估场2使用的均是国家级2400多台站的日降水量标准值,尽管采用的插值算法略有不同,但对2套数据造成的插值结果对比发现:利用初估场1和2得到的不同区域插值误差的交叉检验结果基本一致,区域 2的相对偏差(R Bias)在10.0%以内,区域 1和 3的相对偏差分别超过-20.0%和-30.0%。由于初估场2进一步考虑了坡度、坡向与风向夹角对降水量的影响,因而能更准确得再现降水的分布特征,交叉检验的系统偏差均小于初估场1对应的结果。采用初估场3虽然显著降低了区域1和区域3的相对偏差,如区域1的相对偏差由-21.1%降低到了-5.6%,区域3的相对偏差由-34.2%降低到了-9.1%,但各区域的均方根误差(Rmse)均有所增大,其中区域2的Rmse由0.956增加到了1.250mm/hr。Rmse增大的原因可以从插值数据的时间尺度上得到一定解释:初估场3是由小时数据内插得到的,与用30年气候标准值内插生成的初估场1和2相比,必然包含更大的随机性,其结果将导致随机误差即Rmse变大。

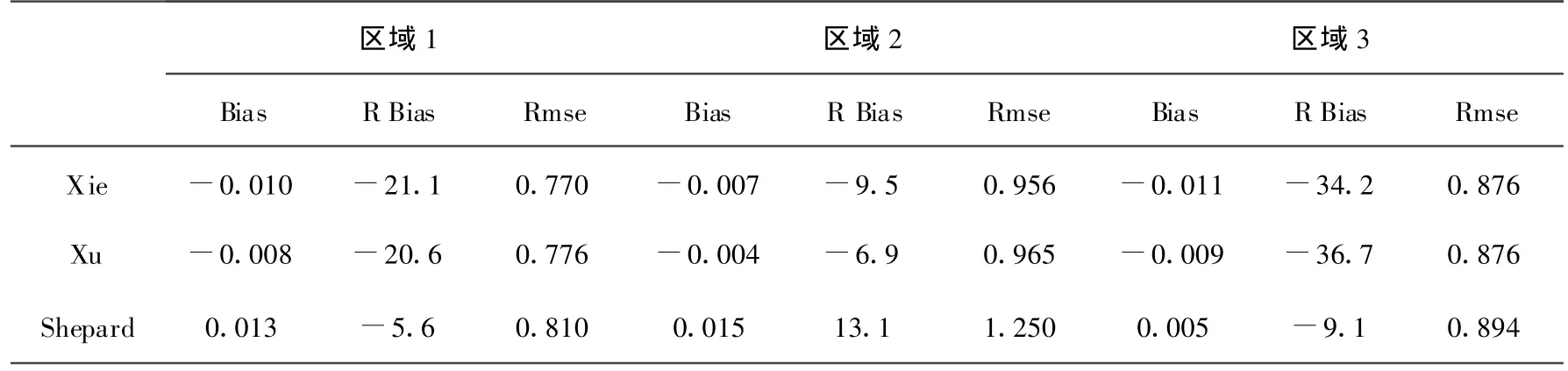
表1 采用3种初估场得到的区域插值误差的交叉检验结果

2 新旧参数下的交叉检验结果

利用优化后的OI核心参数,进一步分析了新旧参数下的交叉检验结果,数据统计时间段是2010年7月,新旧参数在不同区域的交叉检验结果见表2。可见不同区域采用新参数后的均方根误差均小于旧参数下的相应值,如区域2的Rmse由旧参数下的1.409mm/hr减小到了新参数下的1.328mm/hr。说明采用新参数获得的降水量值与站点观测更为接近。新参数在不同区域对应的相关系数也得以提高,如全国平均的相关系数从旧参数下的0.257提高到了新参数下的0.294,说明采用新参数得到的降水空间分布型与站点更为接近。

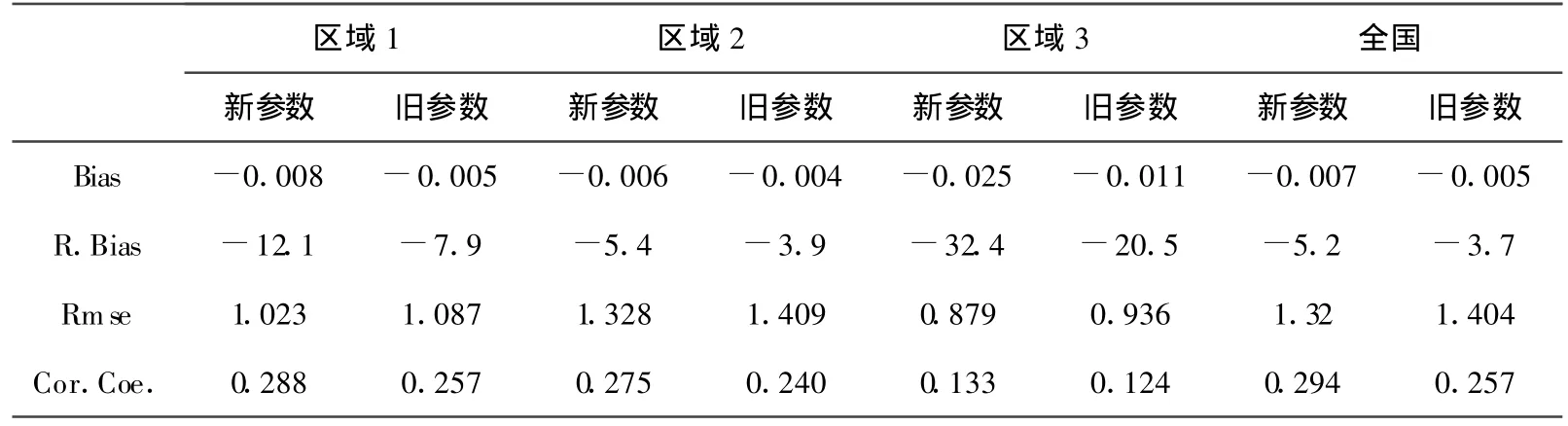
表2 新旧参数下得到的不同区域交叉检验统计结果

进一步统计了新旧参数交叉检验统计指标的频率分布,数据统计时间段是2010年7月,图5仅给出全国平均结果,不同区域的统计结果与全国类似(图略)。从系统偏差(Bias)的频率分布而言:新参数对站点数据的低估较旧参数比例大,而对站点高估的比例小于旧参数。尤其是系统偏差在[-0.005,0]时,旧参数对应的样本百分率为40.6%,而新参数只有28.8%。从Rmse的频率分布看:新、旧参数在Rmse＜1.5mm/hr所占的样本百分率合计为63.3%和56.6%,而旧参数在Rmse≥1.5mm/hr时对应的样本百分率均大于新参数所占的比率,说明新参数能获得更小的均方根误差。新参数得到的相关系数也较旧参数有所提高,如在相关系数比较低的[0,0.2]区间,旧参数出现频率为28.3%,而新参数只占17.3%。随着相关系数的提高,新参数出现高相关系数的频率均比旧参数有所提高,如新参数在相关系数≥0.4的样本百分率为14.1%,而对应的旧参数下只占6.7%。

图5 新旧参数交叉检验统计指标(Bias,Rmse,Cor Coe)的频率分布

3 结论与讨论

OI插值的核心参数包括:数据信噪比、相关随距离的变化关系、搜索半径(或表达成影响台站数)以及初估场等。进一步考虑自动站的空间分布将中国分成了三大区域,探讨了利用OI对全国3万多个自动站小时降水数据进行空间分析时核心参数的优化和确定方法。研究表明:“优化的”数据信噪比约为0.3,相关随距离增加呈e指数递减关系;当站网密度差异较大时,通过确定影响台站数来进行空间插值,一方面可以提高站点稠密区的插值效率,另一方面可以提高站点相对稀疏区的插值精度。另外,初估场对插值结果也有影响,认为采用气候标准值生成的初估场能显著降低插值结果的随机误差,结果比采用同时刻的降水分析场作为初估场更稳定。进一步采用站点交叉检验的方法对新旧参数下的插值结果(以2010年7月数据)进行了对比分析:新参数对应的均方根误差均比旧方案小,而空间相关系数有一定提高,说明采用新参数能获得更加可靠真实的1小时、0.1°分辨率的降水量分析场。

为了进一步提高中国站点稀疏区的小时降水资料质量,已将卫星反演的降水产品(CMORPH和FY)融合到了自动站降水量空间分析场中,获得了质量和时空分辨率均更高的1小时、0.1°分辨率的降水量融合资料,产品已在中国气象科学数据共享网实时发布(cdc.cma.gov.cn)。

致谢:文章中使用的OI插值程序(FORTRAN语言)由NOAA气候预测中心Xie Pingping博士提供,在此深表感谢。

[1] Cressman G P.An operational objective analysis system[J].Mon.Wea.Rev.,1959,87:367-374.

[2] Gandin L S.Objective Analysis of meteorological fields[J].Israel Program for Scientific Translations,1965,242.

[3] Shepard D.A two dimensional interpolation function for irregularly spaced data[C].Prod.23rd National Conf.of the Association for Computing Machinery,Princeton,NJ,ACM,1968:517-524.

[4] New,M,M Hulme,P Jones.Representing twentieth century space-time climate variability.Part I:Development of a 1961-90 mean monthly terrestrial climatology[J].J.Climate,1999,12:829-856.

[5] New M,G M Hulme,P D Jones.Representing Twentieth-Century Space Time Climate Variability.Part II:Development of 1901-96 Monthly Grids of Terrestrial Surface Climate[J].J.Climate,2000,13:2217-2238.

[6] Rudolf B.Management and analysis of precipitation data on a routine basis[C].Proc.Int.Symp.on Precipitation and Evaporation,Bratislava,Slovakia,WMO,1993:69-76.

[7] Schneider U.The GPCC quality-control system for gauge measured precipitation data[C].Proc.Analysis Methods for Precipitation on a Global Scale:Report of a GEWEX Workshop,WCRP-81,WMO/TD-588,Koblenz,Germany,1993.

[8] Hutchinson M F.Interpolating mean rainfall using thin plate smoothing splines[J].Int.J.Geogr.Inf.Syst.,1995,9:385-403.

[9] Chen M,Xie P,Janowiak J E.Global land precipitation:A 50-yr monthly analysis based on gauge observations[J].J.Hydrometeorol,2002,(3):249-266.

[10] Rudolf B,U Schneider.Calculation of gridded precipitation data for the global land-surface using in-situ gauge observations[C].Proc.the 2nd Workshop of the International Precipitation Working Group IPWG,Monterey,2004,231-247.

[11] Chen M,W Shi,P Xie.2008:Assessing objective techniques for gauge-based analyses of global daily precipitation[J].J.Geophys.Res.,2008,113.

[12] 李春晖,梁建茵.基于Shepard和OI方法对雨量计逐时资料的分析[J].应用气象学报,2010,21(4):416-422.

[13] 任芝花,赵平,张强,等.适用于全国自动站小时降水资料的质量控制方法[J].气象,2010,36(7):123-132.

[14] Xie P P,Yatagai A,Chen M,et al.A gauge-based analysis of daily precipitation over East Asia[J].J.Hydrometeor,2007,8:607-626.

[15] 沈艳,冯明农,张洪政,等.我国逐日降水量格点化方法[J].应用气象学报,2010,21(3):279-286.

[16] 徐宾.中国地面降水逐日气候背景0.25°格点场数据集说明文档[J].2009.

[18] Arkin P A,Ardanuy P E.Estimating climatic-scale precipitation from space:A review[J].J Climate,1989,(2):1229-1238.

[19] Barrett E C,Martin D W.The user of satellite data in rainfall monitoring[M].Academic Press,1981.

[20] Franke R.Smooth interpolation of scattered data by local thin plate splines[J].Comput.Math.Appl.,1982,8:273-281.

[21] Huffman G J.Estimates of Root-Mean-Square Random Error for Finite Samples of Estimated Precipitation[J].Journal of Applied Meteorology,1997,36(9):1191-1201.