GRAPES-Meso 模式动力框架与物理过程对预报误差影响研究
2012-01-05张涵斌龙柯吉
张涵斌, 陈 静, 龙柯吉
(1.成都信息工程学院,四川 成都 610025;2.国家数值预报中心,北京 100081;3.四川省气象局,四川 成都610025)
0 引言
自2000年以来,中国气象局自主开发了新一代全球/区域同化预报系统(Global/Regional Assimilation and Prediction Enhanced System,GRAPES)[1-3]。GRAPES模式系统主要包括资料同化系统、多尺度有限区域与全球模式通用的动力框架以及物理过程参数化方案[4]。资料同化系统采用三维变分,现在正逐步向四维变分过渡[2-3];动力框架采用静力/非静力可变,半隐式-半拉格朗日计算方案,能够降低计算成本[1-2],并逐步走向精细化[4];物理过程参数化经过对国际先进参数化方案的优选与优化,形成了辐射,边界层、陆面过程参数化,积云对流参数化和微物理过程等多种适合研究和预报应用的方案[1-3],并逐步针对中国天气特点进行着优化改进[4]。
集合预报系统是GRAPES的重要发展方向[5-7]。近年来,GRAPES区域模式集合预报初值扰动技术研究取得了一些进展。谭燕等[8]、纪永明[9]、龙柯吉等[10]研究了GRAPES区域模式区域集合预报技术,总体来看,GRAPES集合成员发散度不够,没能反映GRAPES模式自身的误差特征。一个合理的集合预报系统需要对GRAPES模式误差特点进行更多的研究,捕获到GRAPES模式误差的主要影响因素。中国有不少学者已经研究了GRAPES全球和区域模式预报误差特征。叶成志,欧阳里程等[11]指出,GRAPES区域中尺度模式预报能力随预报时效延长而下降,预报误差随预报时效延长而增长。王雨等[12]指出GRAPES模式对降水预报存在雨量偏大的问题。庄照荣等[13]指出在集合卡尔曼滤波同化系统中,模式误差是不可忽略的因素,并用不同分辨率的模式预报差异估计了GRAPES全球模式的模式误差,研究发现模式误差随着分辨率降低而线性增加,而且模式误差随着预报时效的增加呈现线性增长的趋势。
过去的研究表明,区域模式预报误差主要来源于初值、模式和边界条件[14-16],在模式误差中,模式动力框架和物理过程参数化方案是模式误差的主要影响因素,GRAPES动力框架误差特征是什么?物理过程对预报误差的影响特征究竟是什么?目前对这方面研究分析较少,因此,研究GRAPES-Meso模式动力框架与物理过程对预报误差影响,对改进GRAPES模式发展GRAPES集合预报具有重要意义。利用GRAPES中尺度模式,对不同类型天气过程(强降水、中等强度降水、弱降水)进行数值模拟试验,研究GRAPES区域模式误差影响因素,分析模式动力框架和参数化方案对预报误差的影响特征,为改进GRAPES模式和发展GRAPES集合预报技术提供依据有用的信息。
1 研究个例简介
选取2008年汛期中国区域3种不同类型天气过程(强降水、中等强度降水、弱降水)。强降水过程为2008年7月22日08时至23日08时暴雨过程(图1a),中国黄淮地区普降暴雨到大暴雨,湖北西部和北部、河南大部、山东南部、江苏北部、安徽北部等地24小时累计降水量一般在100~180mm,局部地区降水量达200~240mm;中等强度降雨过程选取2008年7月24日08时至25日08时的降水过程(图1b),四川西部、安徽北部有局部降水,降水量不到100mm;弱降水天气选取2008年6月5日08时至6日08时,除广东南部地区有一些降水外,中国大部地区无明显强降水天气(图1c),图2给出了影响这3种不同天气过程的环流形势,从500hPa位势高度场,风场以及急流的分布可以看出这3个个例的影响系统不同,可以代表不同的环流形势和天气类型。


2 试验方案设计
GRAPES-Meso模式分辨率0.3×0.3度,模式积分区域为70°E~142°E,15°N ~60°N。背景场采用国家气象中心T213全球谱模式预报场,分析时间间隔12h,同时生成GRAPES模式的边界条件。再利用GRAPES三维变分系统同化、探空和地面观测资料对背景场进行同化分析后,获得GRAPES模式初始场。
为了分析模式动力框架和物理过程参数化方案对GRAPES模式误差的影响特征,设计了全物理过程模式和关闭所有物理过程模式(即只考虑动力框架)对比试验,如表1所示。
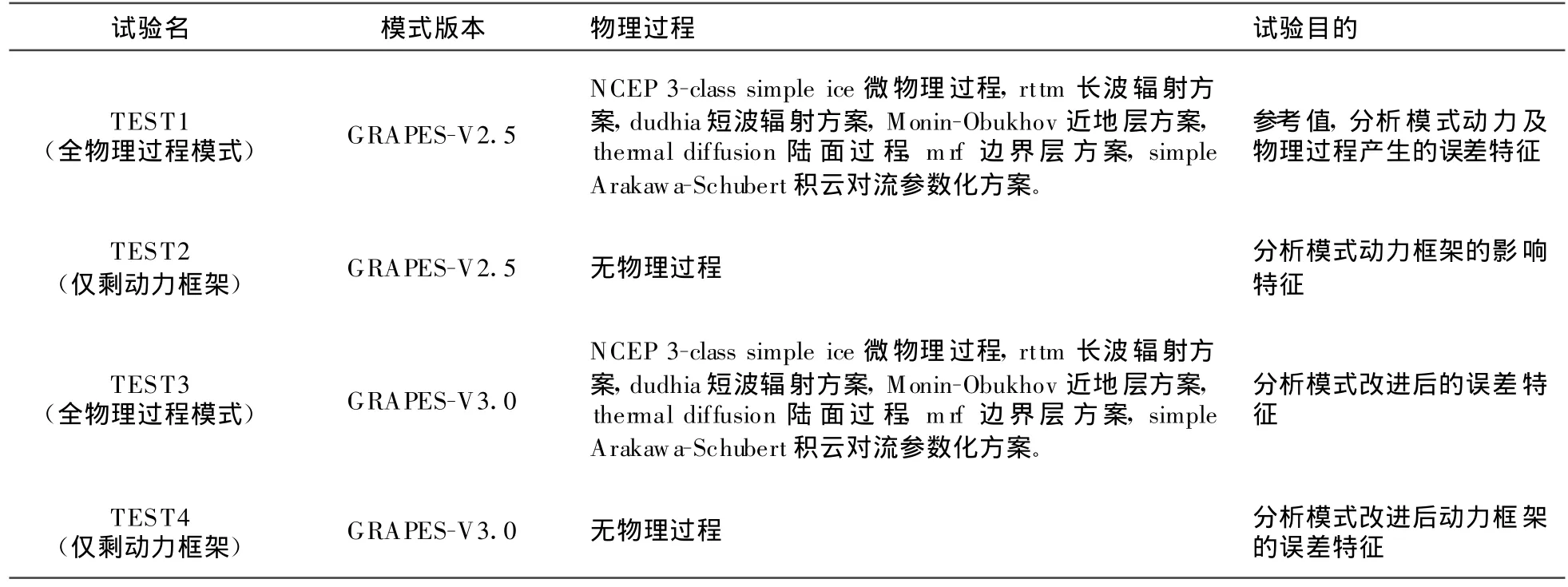
表1 试验方案设计
3 试验结果分析
3.1 形势场及降水偏差
图3是TEST1试验对3个典型过程60h预报时效的24h累积降水预报。与实况对比(图1)可见,2008年7月23日强降水过程的雨带预报存在明显偏差,模式预报主要降水带位于四川南部,重庆,贵州,湖北,安徽以及江浙一带,没有预报出山东地区强降水过程。对2008年7月25日中等强度降水过程,强降水落区存在明显差异,山东东部降水预报偏强,中心值达到了100mm左右,而实况为20mm左右,而河南地区预报偏弱,仅为15mm左右,而河南实况降水为50~100mm。对2008年6月6日中国区域无明显降水的个例,预报与实况较为吻合。
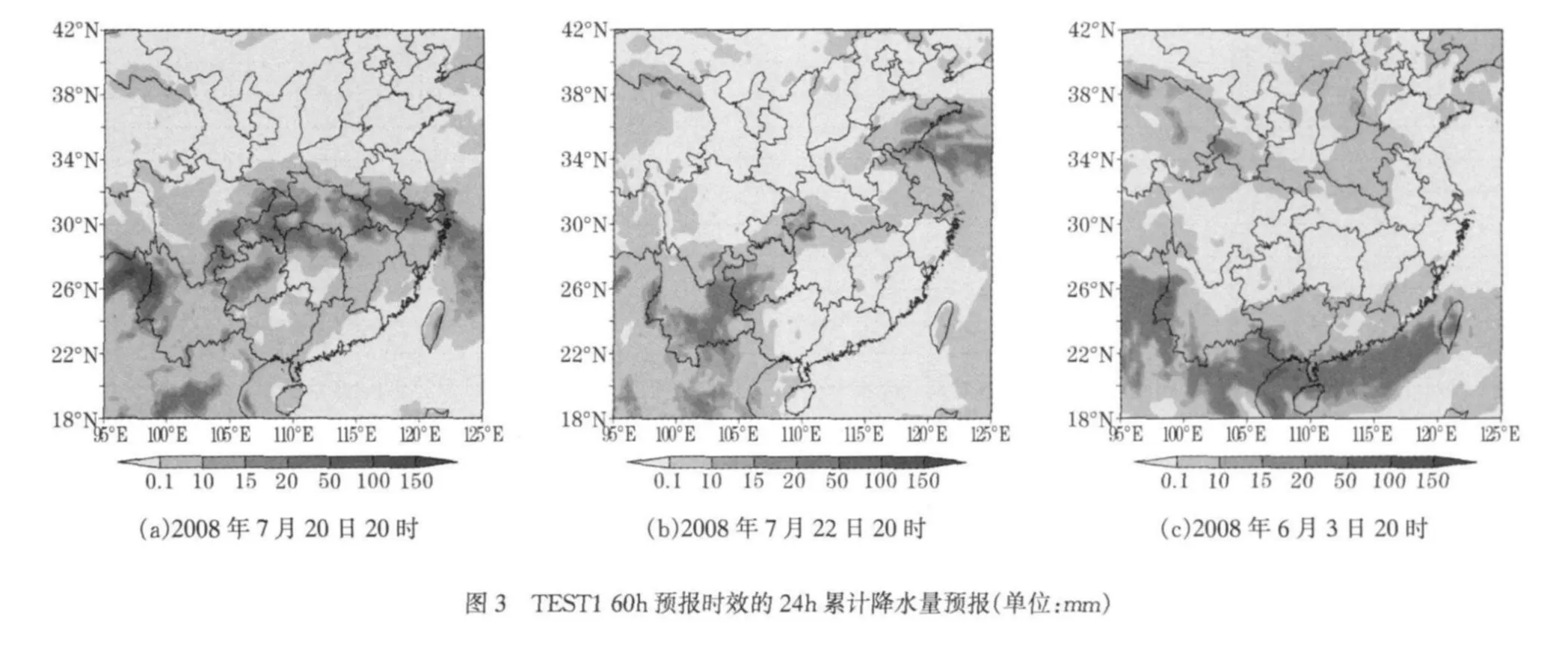
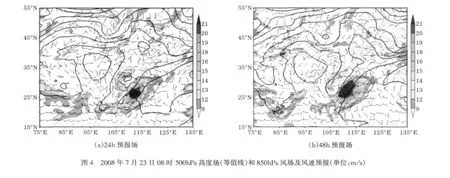
图4给出了TEST1试验对2008年7月23日强降水个例500hPa位势高度场和850hPa风场的24h和48h预报。与实况相比(图2a),随着预报时效的延长,500hPa高度场和850hPa风场预报偏差增长,西南气流风速随预报时效延长明显偏强,其他2个个例误差特征相似(图略)。
3.2 误差分布及成因初步分析
定义等压面上某格点的模式预报误差为GRAPES预报时刻与相应该时刻GRAPES-3D VAR分析场的偏差Ei

其中t 0为预报起始时间,t为预报时效,Ft0+t代表预报场,At0+t代表分析场。
定义绝对偏差 AEi。

3.2.1 平均绝对偏差分布总体特征
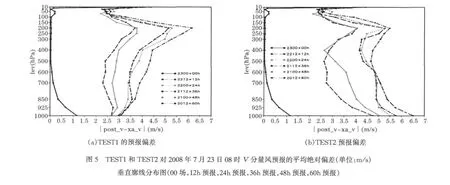
图5为TEST1和TEST2对2008年7月23日08时 V分量风的不同预报时效预报的平均绝对偏差垂直廓线分布图。从图5(a)可以看出,TEST1的预报平均绝对偏差最大值出现在200hPa附近,随预报时效延长,绝对偏差值也增大,TEST2(见图5b)平均绝对偏差同样在200hPa上,且量级相同,表明物理过程参数化方案对200hPa的模式预报偏差影响不显著。值得一提的是,TEST1和TEST2绝对偏差在400hPa以下层次存在较大差异,TEST1低层偏差相对较小,即使随着预报时效的延长,1000hPa偏差也基本保持在3m/s左右;而TEST2,偏差随等压面高度降低而增大,1000hPa误差最大,且随预报时效延长而增加,平均绝对偏差超过6m/s。U分量风平均绝对偏差特征与V分量风类似。
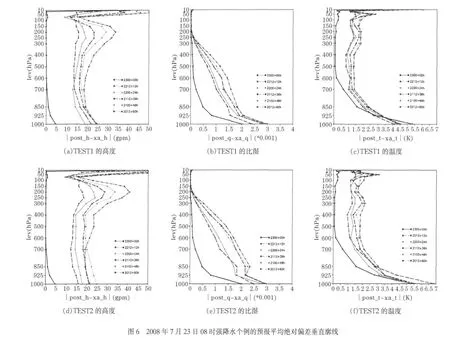
图6是 2008年7月23日强降水个例TEST1和 TEST2的高度(图6a,图6d)、比湿(图6b,图6e)及温度(图6c,图6f)预报平均绝对偏差垂直分布廓线。图6中00h的平均绝对偏差是GRAPES模式系统经过初始化和后处理过程,将初始分析场插值到模式面,再经后处理过程插值到等压面后,与初始分析场的绝对偏差。可看到在700hPa以下层次,00h的高度、比湿、温度与原分析场存在较大的绝对偏差,如925hPa和1000hPa温度绝对偏差分别为3℃左右和5.5℃左右,表明垂直插值过程会在低层大气产生较大的偏差。再看各预报时效的平均绝对偏差垂直分布,高度平均绝对偏差(图6a,图6d)随高度增加而增加,在200hPa达到极大值,如60h高度预报偏差达到40位势米,随后高度偏差开始减小,到50hPa后,高度平均偏差低于低层偏差值,到模式层顶又突然增加,且TEST1和TEST2的分布特征相似。对于比湿(图6b,图6e),偏差随高度增加而减少,这与水汽主要分布在低层有关。在925hPa至1000hPa,TEST1与TEST2的平均绝对偏差特征一致,在925~850hPa,TEST1的偏差较TEST2小,表明物理过程可以改善水汽的预报误差;对于温度(图6c,图6f),预报偏差较大层次依然是100~400hPa左右,如参考00h的绝对偏差值,则动力框架预报偏差垂直廓线比全物理过程参数化方案模式离散。
在注册会计师注册领域强化监管力度,选取品德优秀,专业技能比较强的人才,防止滥竽充数,坚决防止凭关系取得注册会计师资格的举措,在挑选的源头提升注册会计师的品质。在进行管理时,提升注册会计师的待遇,依托高薪养廉的途径让他有自己的生活保障,防止腐败的滋生。顺应时代的潮流方可更好地融入时代,进而可以实现自身的价值。
前面提到GRAPES的00h绝对偏差主要来自垂直插值过程。GRAPES-Meso三维变分同化系统在等压面上进行分析,而预报积分是在模式面上进行,分析对象为预报结果插值到等压面的结果,实况值采用的是GRAPESMeso三维变分同化系统的等压面分析值,这必然包含垂直插值误差。插值误差对模式误差分析的影响如何,对上述结论是否会有影响?以2008年7月23日强降水为例,分析垂直插值过程对误差分布的影响。
图7是2008年7月23日08时的GRAPES-3DVAR的分析场与00h预报场 V分量风偏差在不同高度层的水平分布。由图7(a)~(f)可知,在青藏高原这样的高海拔区,600hPa以下层次已经位于地表以下,预报值均来自垂直插值,这些区域的预报值表现出较大插值偏差,而在其他区域,插值偏差都维持在-0.5~-0.5m/s,随着高度的上升,插值偏差越来越小,500hPa偏差为-0.5至0.5m/s。其他变量分布情况与 V分量风类似。由此可知,插值方案产生的模式预报误差主要出现在高海拔区域,尤其是青藏高原地区,且层次越高,插值误差越小,这种插值误差在TEST1和TEST2中均存在,不会影响上述分析。
对于中等强度以及弱降水个例,TEST1和TEST2的U分量风、V分量风、温度、高度、水汽预报的平均绝对偏差特征都与强降水个例较为一致(图略),表明GRAPES-Meso模式存在较为显著的系统性误差。值得注意的是,TEST2试验的预报结果是模式动力框架获得,没有考虑物理过程,而其偏差特征与全物理过程类似,仅低层动力场预报误差存在一些差别,这表明模式动力框架对预报误差的影响较物理过程大。
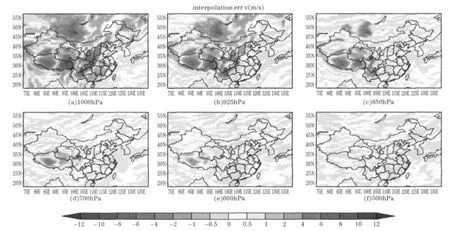
图7 2008年7月23日08时的GRAPES-3DVAR的分析场与00h预报场 V分量风偏差水平分布
3.2.2 预报偏差空间结构特征分析
对预报偏差的水平及垂直分布进行分析,以了解GRAPES模式误差的结构空间形态以及GRAPES模式动力框架与物理过程对预报误差影响相互联系。

图8 TEST1(a,b,c)和TEST2(d,e,f)试验对3个典型个例的700hPa V分量风60h预报相对偏差(单位:m/s)
图8是TEST1和TEST2试验对3个典型个例的700hPa V分量风60h预报偏差分布。从图可见,相同个例的TEST1和TEST2预报偏差分布形态比较相似,如2008年7月20日20时的60h预报(图8a,图8d),青藏高原东侧边缘均有一负偏差区,高原主体上空和云南、贵州、重庆有一正预报偏差区。不同个例偏差分布会有所差异,如2008年7月23日TEST1对山东半岛预报偏差为负偏差,而2008年7月25日个例却为正偏差(图8b及图8e)。此外,3个个例在高原上空的偏差均为正值,表明高原地区存在较大误差,这与GRAPES垂直插值方案误差有关。
图9是2008年7月23日08时强降水个例TEST1和TEST2的 V分量风60h预报偏差沿25°N的垂直剖面图。从图可见TEST1(图9a)和TEST2(图9b)垂直分布形态很相似,在 105°E左右,300hPa至850hPa均存在较明显的正偏差,而在107°E~117°E,则为较明显的负偏差区。
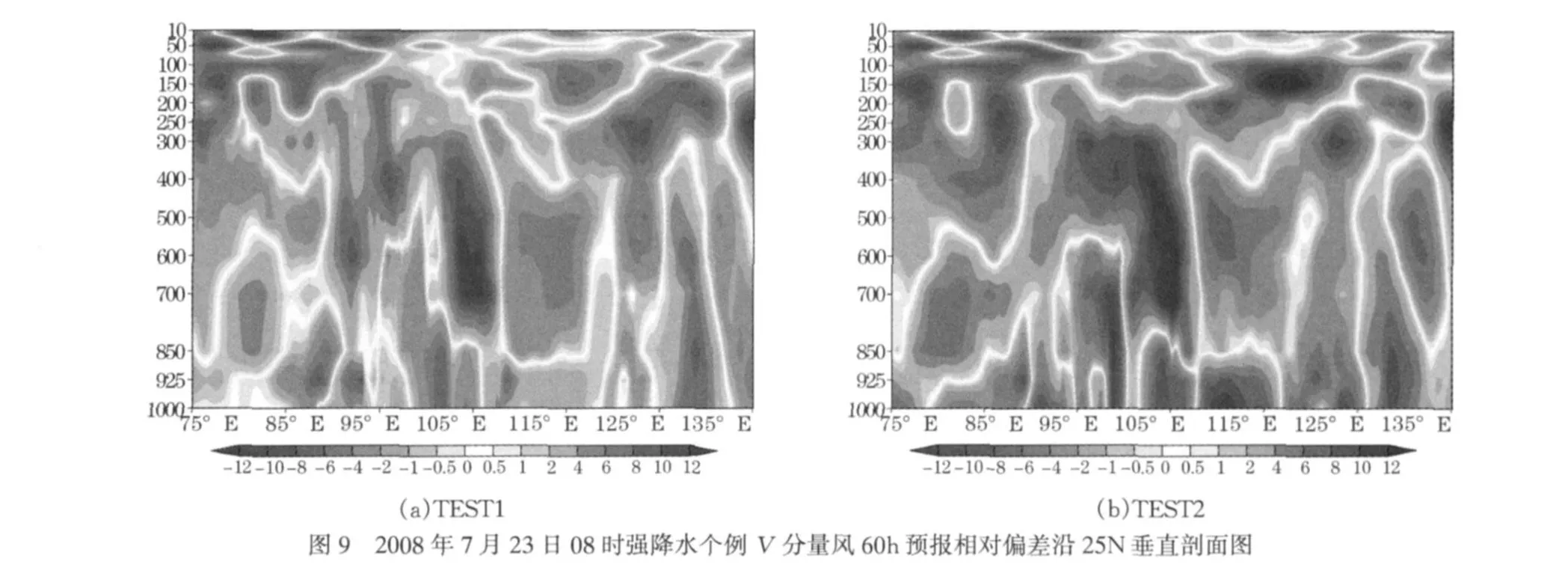
综上所述,动力框架和全物理过程参数化方案预报偏差形态比较相似,动力框架预报误差略大,表明模式误差主要特征是由模式动力框架部分确定,物理过程参数化方案对误差形态有一定的修正,但作用有限,以上结果表明模式动力框架对模式预报误差的分布形态具有较明显的影响,GRAPES-Meso模式的预报误差很大程度上来源于模式动力框架,同时也包含一定的插值误差,低层插值误差更明显。
3.2.3 物理过程参数化方案对误差总体特征的影响
前面的结果表明,GRAPES动力框架对U和V分量风预报误差影响较物理过程大,物理过程参数化方案可减少动力框架预报误差,TEST1中共有7种参数化方案(见表1),哪一种参数化方案对减少误差起主要作用?参数化方案与模式误差又是如何相互影响的?
设计如表2的7个试验方案,分别关掉某个物理过程参数化方案,称为试验wetA,wetB,wetC,wetD,wetE,wetF,wetG,对2008年7月23日08时的强降水个例进行模拟,分析物理过程在减少模式误差中的主要作用,其中比对参考预报场选择表1中的TEST1试验。

表2 物理过程参数化方案影响试验方案
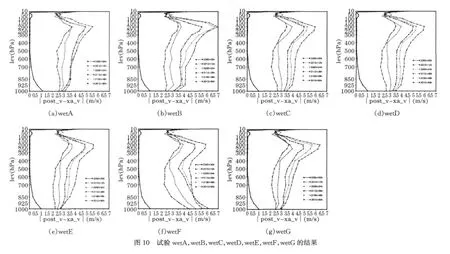
图10为试验wetA,wetB,wetC,wetD,wetE,wetF,wetG的 V分量风平均绝对偏差垂直廓线图。对比图5a和图10可见,6个试验(wetA,wetB,wetC,wetD,wetE,wetG)预报偏差分布特征与TEST1相似,平均绝对偏差仅有一个极大值,位于200hPa,400hpa以下偏差明显减小。而不考虑边界层参数化方案的wetF试验,平均绝对偏差有两个极大值,一个位于1000hPa,一个位于200hPa,12h至60h预报平均绝对偏差为4.5~6.5m/s,500hPa平均绝对偏差值最小(图10f),误差形态与TEST2相似。其它变量如高度、温度和比湿,边界层方案对低层绝对偏差的影响程度不如风场显著(图略),这表明边界层方案对GRAPES模式低层动力场预报误差有重要影响,原因是由于模式边界层方案影响陆气的热量、水汽通量交换,并最终影响动力场预报[17-18]。
4 结束语
为了深入了解GRAPES-Meso区域模式动力框架与物理过程对预报误差的影响,找出GRAPES-Meso模式不确定性的主要来源,为模式的改进和针对GRAPES-Meso集合预报技术的发展提供参考,基于GRAPES中尺度模式,通过设计4组对比试验,对2008年3个不同类型天气过程(强降水、中等强度降水、弱降水)进行数值模拟试验,得出如下结果和结论:
(1)对于不同天气形势下的强降水、中等强度降水、弱降水个例,模式动力框架和全物理过程模式的U分量风、V分量风、温度、高度、水汽预报的总体预报误差特征、误差水平分布与垂直结构都较为一致,预报误差在200hPa高度层左右达到最大。表明GRAPES-Meso模式存在较为显著的系统性误差。进一步分析表明,动力框架对预报误差影响较物理过程更大,参数化方案对误差形态有一定的修正,但作用有限。
(2)GRAPES-Meso模式要素预报从模式面转换到等压面的插值方案对模式层底和模式层顶误差分布有明显的影响,GRAPES-Meso垂直插值方案有待完善。
(3)边界层方案对GRAPES模式低层动力场预报误差有重要影响,引入边界层参数化方案能够显著改善模式动力场在低层的预报误差,原因是由于模式边界层方案影响陆气的热量、水汽通量交换,可显著影响低层动力场预报 。
综上所述,GRAPES-Meso模式误差改进重点在动力框架,在GRAPES-Meso集合预报系统的设计中,需要重点考虑动力框架引起的模式不确定性。基于GRAPES-Meso V3.0进行了同样的试验,对比结果与GRAPESMeso V2.5的基本一致。需要注意的是,对比试验仅针对参数化方案进行了不同的设置,而影响误差的因素有很多,比如模式分辨率,分辨率为0.3度,如果分辨率更高或者更低,对误差的影响又是如何?模式误差又会表现出怎样的分布特征?实验背景场和边界条件选用了T213资料,背景场经过三维变分后的分析场可能会存在一些动力不协调性,导致积分初期的误差增长,侧边界也可能会对预报误差产生影响,这些工作需要进行更多的研究分析。
致谢:感谢数值预报中心陈德辉老师、邓国老师、邓莲堂老师、徐枝芳老师给予的热心帮助。
[1] 陈德辉,杨学胜,胡江林.多尺度通用动力模式框架的设计策略[J].应用气象学报,2003,14(4):452-461.
[2] 陈德辉,沈学顺.新一代数值预报系统GRAPES研究进展[J].应用气象学报,2006,17(6):773-777.
[3] 张人禾,沈学顺.中国国家级新一代业务数值预报系统GRAPES的发展[J].科学通报,2008,53(20):2393-2395.
[4] 薛纪善,陈德辉,等.数值预报系统GRAPES的科学设计与应用[M].北京:科学出版社,2007.
[5] Toth Z,Kalnay E.Ensemble forecasting at NMC:The generation of perturbations[J].Bull Amer Meteor Soc,1993,74:2317-2233.
[6] Toth Zoltan.meeting summary:Ensemble Forecasting in WRF.Bulletin of the American Meteorological Society[J].2001,82:695-697.
[7] Hamill,Thomas M,Steven L.Ensemble Forecasting in the Short to Medium Range:Report from a Workshop[J].Bulletin of the American Meteorological Sociaty,2000,81:2653-2664.
[8] 谭燕.中尺度强降水天气集合预报技术的研究[D].北京:中国气象科学研究院.
[9] 纪永明,陈静,矫梅燕,等.基于多中心T IGGE资料的区域GRAPES集合预报初步试验[J].气象,2011,37(4):392-402.
[10] 龙柯吉,陈静,马旭林,等.基于集合卡尔曼变换的区域集合预报初步研究[J].成都信息工程学院学报,2011,(1):37-46.
[11] 叶成志,欧阳里程,李象玉.GRAPES中尺度模式对2005年长江流域重大灾害性天气过程预报性能的检验分析[J].热带气象学报,2006,26(4):393-399.
[12] 王雨,李丽.GRAPES-Meso V3.0模式预报效果检验[J].应用气象学报,2010,21(5):524-533.
[13] 庄兆荣,薛纪善.GRAPES全球模式的模式误差估计[J].大气科学,2010,34(3):591-598.
[14] Zhang Fuqing,Andrew M Odins,John W.Nielsen-Gammon:Mesoscale predictability of an extreme warm-season precipitation event[J].Weather and Forecasting,2006,21:149-166.
[15] Kalnay,E Atmospheric Modeling.Data Assimilation and Predictability[M].Cambridge university press,2003:196-199.
[16] Harrison M S.Analysis and model dependencies in medium-range forecast:two transplant case studies[J].Quart.J.Roy.Meteor.Soc.1999,126:711-724.
[17] 赵鸣.边界层和陆面过程对中国暴雨影响研究的进展暴雨灾害[J].2008,27(2):186-190.
[18] 肖玉华,何光碧.边界层参数化方案对不同性质降水模拟的影响高原气象[J].2010,29(2):331-339.
