多比例时滞杂交双向联想记忆神经网络的全局指数稳定性
2012-01-05翁良燕周立群
翁良燕,周立群
(天津师范大学 数学科学学院,天津 300387)
的全局指数稳定性.通过构造合适的Lyapunov泛函和应用Halanay型不等式分别得到该系统全局指数稳定的充分条件.
2003年,张伟等研究了时滞杂交BAM神经网络[11]
多比例时滞杂交双向联想记忆神经网络的全局指数稳定性
翁良燕,周立群
(天津师范大学 数学科学学院,天津 300387)
考虑多比例时滞杂交双向联想记忆神经网络的全局指数稳定性.应用Brouwer不动点定理证明了多比例时滞杂交双向联想记忆神经网络平衡点的存在性,再通过构造合适的Lyapunov泛函,获得了该系统平衡点全局指数稳定的时滞依赖的充分条件,该条件蕴含系统平衡点的唯一性,并给出了一个例子说明结论的有效性.
神经网络;双向联想记忆;比例时滞;全局指数稳定性;Lyapunov泛函
1 引言和预备知识
1988年,Kosko提出双向联想记忆(BAM)神经网络[1],随后Kosko又给出BAM神经网络的推广模型[2-4],该模型在信号处理、模式识别、并行计算、联想记忆和复杂优化问题等领域有着广泛的应用.近些年来,人们已经对有时滞或无时滞的BAM神经网络的各种稳定性进行了深入研究[5-11].文献[5]分析了激活函数是连续可微且单增的一类时滞BAM神经网络的全局吸引性;文献[8]在不要求激励函数单调性和可微性的情况下,得到了时变时滞BAM神经网络的鲁棒稳定性的2个新判据;文献[10]基于Lyapunov泛函、Halanay型不等式研究了时滞杂交BAM神经网络的全局指数稳定性.
2002年,陈安平等研究了时滞联想记忆神经网络[7]

的全局稳定性,利用Lyapunov泛函方法获得了该系统全局渐近稳定和全局指数稳定的充分条件.
2003年,廖晓峰等研究了具分布时滞杂交BAM神经网络[10]
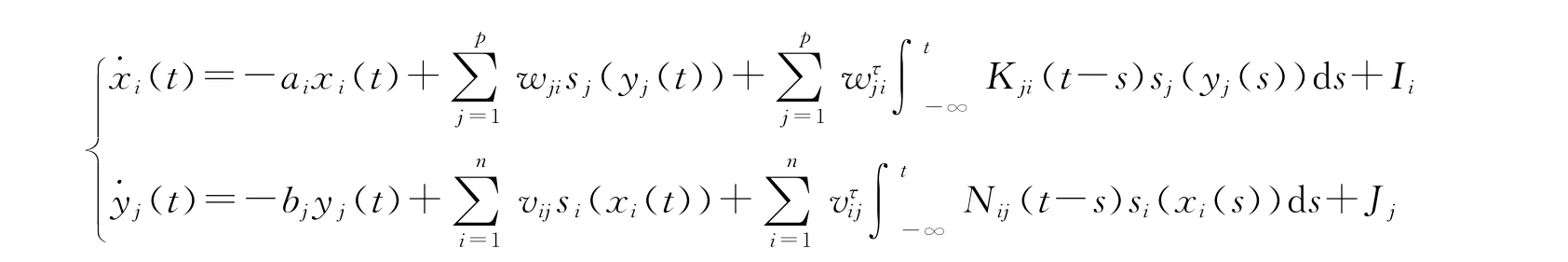
的全局指数稳定性.通过构造合适的Lyapunov泛函和应用Halanay型不等式分别得到该系统全局指数稳定的充分条件.
2003年,张伟等研究了时滞杂交BAM神经网络[11]

的全局指数稳定性.应用Halanay型不等式得到该系统全局指数稳定的充分条件.
目前关于时滞神经网络稳定性的研究大多为具常时滞、变时滞、分布时滞等类型[9-15],而关于比例时滞神经网络[16]的研究结果较少.本研究通过构造合适的Lyapunov泛函,讨论一类具多比例时滞杂交BAM神经网络的全局指数稳定性.
考虑如下神经网络模型:


2 主要结果

那么系统(3)的平衡点是唯一的,并且是全局指数稳定的.
证明由于系统平衡点的全局指数稳定性蕴含系统平衡点的唯一性,因此只需证明系统(3)平衡点的全局指数稳定性即可.定义


3 数值例子

满足定理2的条件,因此系统(11)是全局指数稳定的.
4 结论
在激活函数满足有界且全局Lipschitz连续条件下,研究了一类具多比例时滞杂交BAM神经网络的全局指数稳定性.首先通过变换ui(t)=x i(et),vj(t)=y j(et)将具多比例时滞杂交BAM 神经网络(1)等价变换为具变系数常时滞杂交BAM神经网络(3),然后应用Brouwer不动点定理证明了该系统至少存在一个平衡点,再通过构造合适的Lyapunov泛函和运用不等式技巧,得到该系统全局指数稳定的一个时滞依赖的充分条件,又根据系统平衡点的全局指数稳定性蕴含着系统平衡点的唯一性,进而证明了此系统平衡点的唯一性,并给出了例子说明所得结论的正确性.
[1] KOSKO B.Bidirectional associative memories[J].IEEE Transactions on Systems,Man and Cybernetics,1988,18(10):49-60.
[2] KOSKO B.Unsupervised learning in noise[J].IEEE Transactions on Neural Networks,1991,1(1):44-57.
[3] KOSKO B.Neural Networks and Fuzzy Systems—A Dynamical System Approach to Machine Intelligence[M].Englewood Cliffs,NJ:Prentice-Hall,1992.
[4] KOSKO B.Structural stability of unsupervised learning in feedback neural networks[J].IEEE Transactions on Automatic Control,1991,36(5):785-790.
[5] 廖晓峰,吴忠福,秦拯.依赖时延BAM神经网络的全局吸引性分析[J].计算机研究与发展,2000,37(7):833-837.
[6] 周进,刘增荣.具有时滞的双向联想记忆(BAM)的神经网络的全局动力学行为[J].应用数学与力学,2005,26(3):300-307.
[7] 陈安平,高守平.时滞(BAM)的神经网络的全局稳定性[J].应用基础与工程科学学报,2002,10(1):95-101.
[8] 王占山,光焕新.带时变时滞双向联想记忆细胞神经网络的鲁棒稳定性[J].吉林大学学报:工学版,2007,37(6):1398-1401.
[9] 武怀勤,孙建枝.时滞BAM神经网络周期震荡解的存在性和指数收敛性[J].五邑大学学报:自然科学版,2008,22(1):31-34.
[10] LIAO X F,WONG K W.Convergence dynamics of hybrid bidirectional associative memory neural networks with distributed delays[J].Phys Lett,2003,A(318):55-64.
[11] 张伟,廖晓峰.时滞杂交双向联想记忆神经网络的全局指数稳定性[J].计算机研究与发展,2003,40(10):1410-1413.
[12] 周立群.随机延时神经细胞网络的几乎必然指数稳定性[J].天津师范大学学报:自然科学版,2007,27(4):35-42.
[13] 周立群,张艳艳,王贵君.一类延时细胞神经网络的指数周期性与稳定性[J].系统仿真学报,2010,22(3):634-641.
[14] ZHANG Y,HENG P A,LEUNG S K.Convergence analysis of cellular neural networks[J].IEEE Transactions on Circuits and Systems,2001,48(6):680-687.
[15] YANG Y Q,CAO J.Stability and periodicity in delayed cellular neural networks with impulsive effects[J].Nonlinear Analysis:Real World Applications,2007,8(2):362-374.
[16] ZHOU L Q.On the global dissipativity of a class of cellular neural networks with multipantograph delays[J].Advances in Artificial Neural Systems,2011(10):1155-1161.
[17] LIU Y K.Asymptotic behavior of functional-differential equations with priporyial time delays[J].Eur J Appl Math,1996,7(1):1-30.
Global exponential stability of hybrid bi-directional associative memory neural networks with multi-pantograph delays
WENGLiang-yan,ZHOULi-qun
(College of Mathematical Science,Tianjin Normal University,Tianjin 300387,China)
The global exponential stability of hybrid bi-directional associative memory(BAM)neural networks with multi-pantograph delays is studied.By using Brouwer fixed point theorem,the existence of equilibrium point of this system is proved.And a delay-dependent sufficient condition is derived for the global exponential stability of this system based on the construction of suitable Lyapunov functional.This condition implies the uniqueness of equilibrium point of this system.And an example is given to illustrate the effectiveness of the results.
neural networks;BAM;pantograph delays;global exponential stability;Lyapunov functional
O175.13;TP183
A
1671-1114(2012)03-0018-06
2011-12-19
翁良燕(1988—),女,硕士研究生.
周立群(1972—),女,副教授,博士,主要从事神经网络的稳定性与收敛性、随机微分方程数值方法的稳定性与收敛性方面的研究.
(责任编校 马新光)
