卫星重力梯度数据确定地球重力场的Slepian局部谱分析方法
2012-01-04朱广彬李建成文汉江常晓涛王正涛邹贤才
朱广彬,李建成,文汉江,常晓涛,王正涛,邹贤才
1.国家测绘地理信息局卫星测绘应用中心,北京100830;2.武汉大学测绘学院,湖北武汉430079;3.中国测绘科学研究院,北京100830
卫星重力梯度数据确定地球重力场的Slepian局部谱分析方法
朱广彬1,李建成2,文汉江3,常晓涛1,王正涛2,邹贤才2
1.国家测绘地理信息局卫星测绘应用中心,北京100830;2.武汉大学测绘学院,湖北武汉430079;3.中国测绘科学研究院,北京100830
在引入Slepian局部谱分析方法的基础上,详细分析Slepian函数的数学特性,采用Grünbaum算子提高Slepian方法求解的稳定性和效率,推导卫星重力梯度数据确定地球重力场的Slepian方法表达式。通过仿真分析,就Slepian方法在卫星重力梯度数据确定地球重力位模型中的应用和前景进行分析和讨论。研究表明,Slepian函数在整个球面和球带上具有双正交性,其频谱能量分布特性与卫星轨道的测量特点具有很好的一致性。Slepian低次项系数精度受到极空白影响很小,较之球谐系数低次项明显改善。Slepian方法对大地水准面空间分布恢复精度的直接贡献不明显。
卫星重力梯度;重力场;Slepian局部谱分析;极空白;面球谐函数;Slepian函数
1 引 言
随着空间技术的发展,利用卫星重力技术获取地球重力场精细结构的探测方法得到了不断发展。CHAMP(chanllenging mini-satellite payload)、GRACE(gravity recovery and climate experiment)以及GOCE(gravity field and steadystate ocean circulation explorer)[1-3]卫星任务就是此技术背景下的产物。全球重力位模型可以用球谐系数进行表达,可以看做是观测数据以面球谐函数为基函数在球面上的正交展开。这就需要覆盖全球的重力场数据,即卫星以极轨飞行,否则面球谐函数将不满足其球面正交的特性。但是由于各种工程技术问题,目前的卫星任务均是以近极轨飞行,这就带来了地球两极各有一个小的数据空白区域,也就是极空白问题。
极空白问题导致了在地球重力位模型的解算中,低次球谐系数的估计精度较低[4]。目前解决极空白问题的方案,一是利用已有的重力位模型、航空和地面等重力数据对极空白区域进行数据填充[5],使其满足球谐系数的正交性,但这会带来先验信息的引入;二是利用数理统计方法降低或消除极空白问题的影响,包括正则化方法等[6-8];三是对原有基函数的非正交特性进行数学处理或者引入新的正交函数,从本质上解决极空白问题所带来的影响,包括Cholesky分解、特征值分析、Gram矩阵法等正交处理策略以及Slepian[9]局部谱分析方法等[10-14]。
本文推导利用卫星重力梯度数据反演地球位模型的Slepian局部谱分析方法表达式,研究Slepian函数的数学特性。在此基础上,利用卫星重力梯度模拟数据分析Slepian方法在求解地球重力位模型中的优点和不足。
2 Slepian方法的引入与求解
地球重力场量y(r)(r表示坐标向量)在频域上是具有无限带宽的,但是在进行参数估计时,仅仅能获得一定带宽内的估计值,即估计量是具有频域带限特征的。构建一种新的带限基函数g(r),表示为面球谐函数的线性组合形式
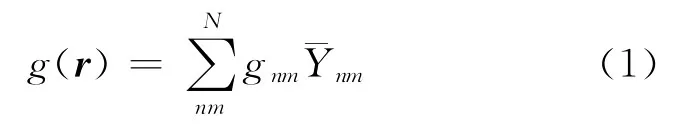
式中,gnm为待求系数。
地球重力场量的带限估计值可以写为
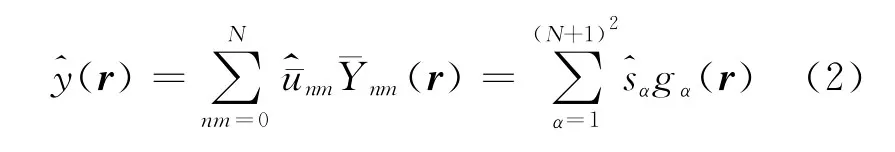
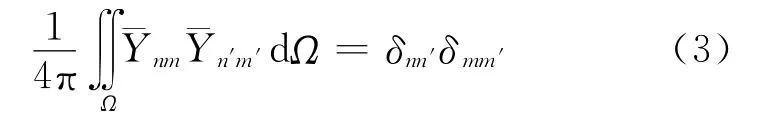
式中,Ω代表整个球面;δ为Kronecker符号。
在利用卫星观测数据求解地球重力位模型的过程中,两极数据空白带来了面球谐函数的不正交问题。如果新的带限函数能最大限度地获取球面中带为极空白球冠的余纬半径,对应于GOCE任务,约为6.7°)上的观测信息,即在球面上具有局部最优特性,则该问题可以得到较为圆满的解决。为此,令新的带限函数的频谱能量在球带B上最大,即
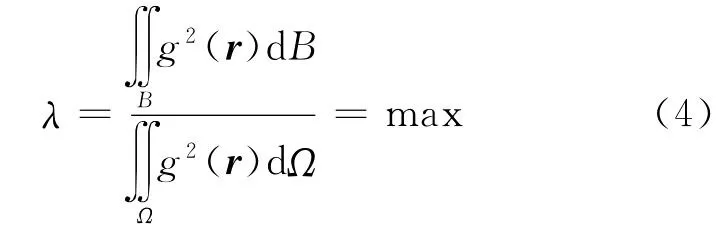
此即所谓的Slepian问题[9,12-14]。
在Slepian问题中,比值0<λ<1作为频域带限函数g(r)空域集中度的一种度量。联合式(1)、式(3)、式(4),可将Slepian问题转化为N+1个(N-m+1)×(N-m+1)维实特征值问题[13-14]

式中,矩阵元素利用式(7)计算[7,15]

式中,¯Fnmk为倾角函数;E[·]代表取整算子。
对每一个特征值问题,将特征值λ1、λ2、…、λ(N-m+1)和相应的特征向量g1、g2、…、g(N-m+1)按照1>λ1≥λ2≥…≥λ(N-m+1)>0进行排序,由于不存在能量完全集中于球带B上的带限基函数,故最大特征值λ1非常接近于1但不等于1。同样,矩阵Dm的正定性保证了最小特征值λ(N-m+1)非常接近于零但不等于零。相应的带限函数g1(r)、g2(r)、…、g(N-m+1)(r)满足双正交性


写成矩阵形式为

Slepian函数在整个球面和球带上均是正交的,其本质可看做是同次面球谐函数的线性组合形式,次数m对于Slepian函数和面球谐函数具有相同意义。
3 Slepian函数的性质
Slepian函数中,在球带B上能量较大的特征函数gα(r)所对应的特征值λα接近于1,称之为有效特征值;而在球带B上能量较小的特征函数的特征值λα则接近于零,称之为无效特征值。这些特征值的大小反映了其所对应的特征向量的能量大小。与最大特征值相对应的基函数g1(r)是在球带B上能量最大的带限函数,g2(r)则是仅次于g1(r)且与其正交的在球带B上能量最大的带限函数,依此类推。当极空白区域较小时,有效特征值较多,无效特征值相对很少,反之亦然。图1给出了N=100,θ0=6.7°时的特征函数gα(r)的特征值分布。图中显示,由于极空白区域很小,绝大多数的特征值均接近于1,仅有小部分的特征值接近于零,而位于这两种情况中间的过渡带相对较短,仅有极少数特征值。

图1 Slepian函数的特征值分布ig.1 The distribution of Slepian function eigenvalues
图2给出了N=18、极空白半径θ0=40°、次数0≤m≤3时的能量占前3位和后3位的Slepian函数纬向分布图(不考虑经向变化)。特征值截至小数点后6位。具有最大权重(λ≈1)的前3位特征函数中,能量非常好地集中于40°≤θ≤140°的范围上,在其他区域上则基本为零。相反的,具有最小权重(λ≈0)的前3位特征函数中,能量非常好地集中于0°≤θ≤40°以及140°≤θ≤180°的范围上。通过这种分布,Slepian函数实现了将卫星观测信息最大化地聚集在非极空白区域,即保证了卫星轨道的测量特点与数据处理方法的一致性。

图2 前3位和后3位特征函数纬向变化图Fig.2 Co-latitudinal dependence of the first three and last three eigenfunctions
此外,从图2可以观察到,当α为奇数时,特征函数为一以赤道为对称轴的偶函数;当α为偶数时,特征函数为一奇函数。当m为偶数时,具有最小权重的特征函数的奇偶性与N的奇偶性相同;当m为奇数时,具有最小权重的特征函数的奇偶性与N的奇偶性相反。也就是说,特征函数的奇偶性与α-m的奇偶性相反。当α=1时,特征函数不具有零点;当α=2时,只有一个零点;当α=3时,特征函数有两个零点,依此类推。也就是说随着α的增加,特征函数的零点个数逐渐增加。
4 数值计算效率和稳定性的改进
当极空白的球冠半径较小时,式(7)的对角化运算会变得很不稳定,特征向量的求解存在不唯一性。另一方面,在求解特征值时,需要通过数值积分或者其他方法计算每一个矩阵元素,总的运算次数为o(N2),这大大增加了运算时间。这里引入一个二阶差分算子Grünbaum算子[13-14,16-17]


引入一(N-m+1)×(N-m+1)矩阵Tm,矩阵元素为

矩阵Dm与Tm均为对称阵,且满足DmTm=TmDm,即二者为可交换矩阵。由于可交换矩阵具有相同的特征向量,故式(5)等价于特征值问题

式中,I为Grünbaum算子;Λ≠λ为相应的Grünbaum特征值。
Grünbaum矩阵Tm可以利用下式进行计算得到[13-14]

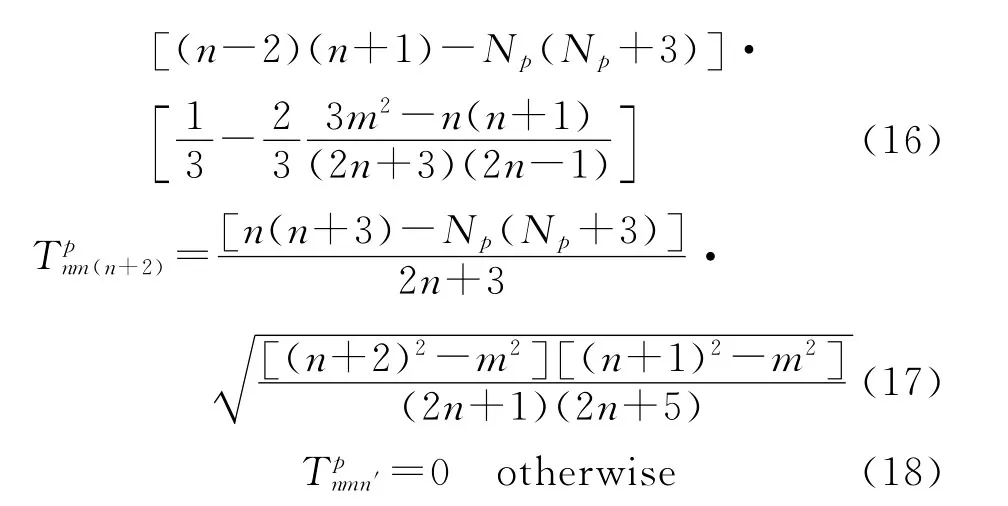
Tm=为一三对角阵,这在很大程度上降低了计算的复杂度,另一方面,Grünbaum算子的运用提高了数值计算的稳定性。由此实现了Slepian问题的稳定快速求解。
图3显示了采用Grünbaum矩阵进行求解后的Slepian函数的二维空间分布图(红蓝分别代表正负值)。从中可以发现,由于经向的正负交叉点与三角函数sin mλ或者cos mλ的性质有关,因此当m=0时,经向上不存在零点;m=±1时,经线上存在两个零点;m=±2时,经线上存在4个零点,依此类推。空间分布图的纬向分布特征与图2的分析一致。
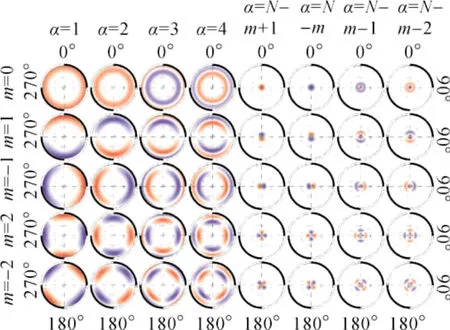
图3 前4位和后4位特征函数的空间分布图(90°<θ<180°)Fig.3 Spatial dependence of the first four and last four eigenfunctions(90°<θ<180°)
图4为勒让德函数和Slepian函数纬向空间分布图(不考虑经向变化),最高阶数为100,次数固定为m=0。图中可以看出,与勒让德函数的频谱分布较为均匀不同,Slepian函数的频谱能量随着纬度增加逐渐减小,在两极地区达到最小,这种数学特性与卫星大地测量中的极空白问题符合很好。这也是引入Slepian函数的主要初衷。而且,频谱能量与阶数密切相关,阶数越高,能量逐渐变小甚至消失。

图4 勒让德函数与Slepian函数的纬向频谱分布Fig.4 Co-latitudinal dependence of Legendre function and Slepian function
5 Slepian方法在卫星重力梯度数据恢复地球重力场中的应用研究
5.1 引力梯度分量的Slepian函数表达
由式(11)可知,Gm为解特征值问题(式(5))所得的特征向量矩阵,为一正交矩阵,故


则对于平方可积空间L2(σ)内相应的线性延拓算子有
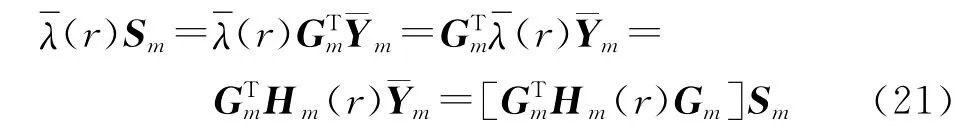
可见,Slepian函数的延拓矩阵为非对角阵形式。
将引力位在地心球坐标系(r,θ,λ)下利用Slepian函数进行展开得到(截断至N阶)

根据引力梯度分量在地心球坐标(r,θ,λ)与局部指北坐标(x,y,z)之间的转换关系[18],可得到引力梯度分量的Slepian函数表达式为(截断至N阶)

根据式(23)在最小二乘框架下求解即可得到Slepian系数

式中,P为权阵;A为相应的设计矩阵;l为梯度观测值向量。
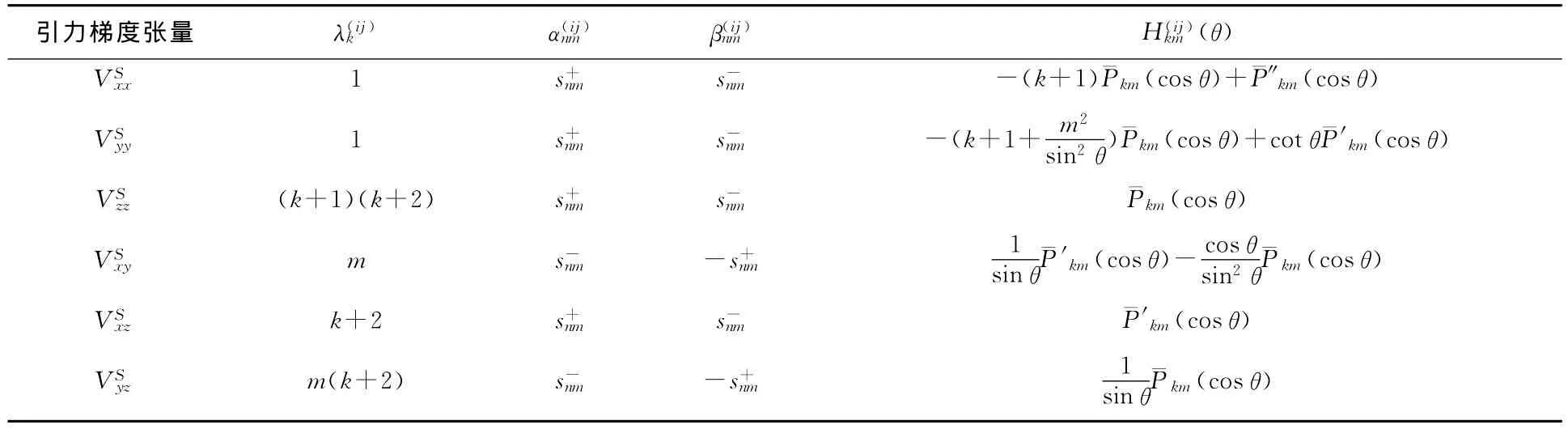
表1 局部指北坐标系下的引力梯度分量Slepian函数表达式Tab.1 Slepian expression of gravity gradient exponents in local north-oriented coordinates
5.2 卫星重力梯度数据恢复地球重力场的Slepian方法仿真分析
基于德国波恩大学提供的GOCE卫星轨道仿真数据,利用EIGEN-GL04C位模型的前300阶模拟了30d、5s采样的卫星重力梯度观测值。利用梯度径向分量Vzz,基于空域最小二乘方法[8,19]进行地球重力位模型的解算。为使得模拟方案更符合GOCE重力位模型实际解算情况,阶数仅取至200阶。图5给出了以面球谐函数为基函数的球谐系数解的相对误差以及以Slepian函数为基函数的Slepian解的相对误差。
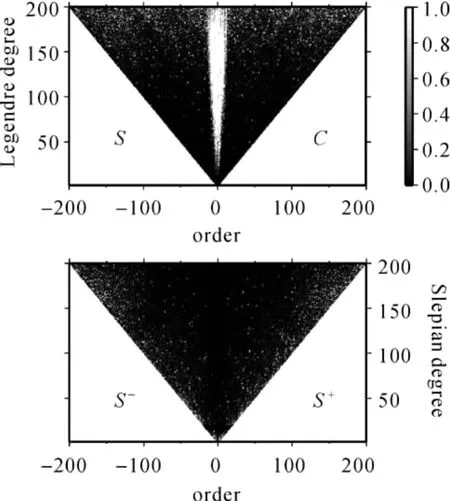
图5 球谐解的相对误差与Slepian解的相对误差比较Fig.5 The relative errors of spherical harmonic solution and Slepian solution
从图5可以看出,由于混频效应的影响,球谐系数解的低次项的估计精度较低,此外高阶项的求解精度亦受到很大影响。将求解过程转换至Slepian域后,求解结果明显变优。低次项的估计精度有了大幅度的提高,高阶项的求解精度也有所提高,但是扇谐项及其周围系数的精度要低一些。对于球谐系数解来讲,混频效应主要包括两部分:第1部分是200阶以上的重力场信号混叠进200阶以下的重力场信号引起;第2部分是地球重力场非极空白区域的观测信息混叠进极空白区域引起的重力场频谱的变化,由于低次勒让德函数在高纬度地区包含更多的能量信号,故而低次项球谐系数的估计精度较低[4]。就Slepian系数解而言,混频效应主要是高阶项(大于200阶)的重力场信号混叠进低阶项所致,且主要影响Slepian函数的扇谐项及其周围系数。
图6显示了球谐系数解和Slepian解的空间域结果。为了便于量级上的比较,这里对低次项进行了截断。图中可以发现,Slepian解较之球谐系数解的大地水准面误差均方差并没有明显的改善。这说明,Slepian解对于大地水准面的求解并没有直接的帮助,大地水准面精度的提高还是需要依赖于高精度的海量观测值的获取。当存在噪声时,需要借助数理统计方法,特别是正则化方法进行处理。Slepian方法的主要贡献在于其开辟了Slepian频域的新范畴,且模型在该频域内的求解精度较之传统的球谐域要高。如何结合数理统计方法在Slepian域内对求解结果进行有效处理,以提高大地水准面的求解精度,有待进一步的研究和分析。
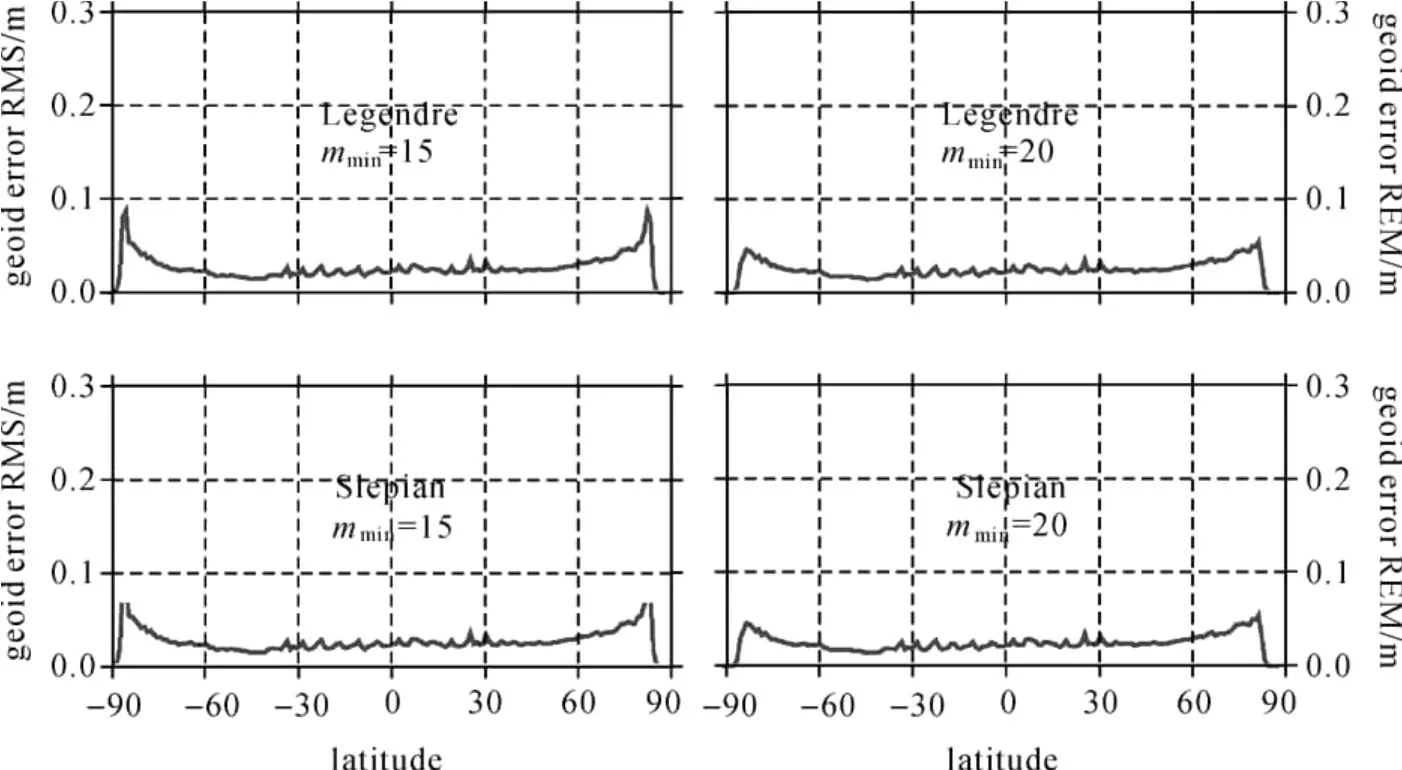
图6 球谐解与Slepian解的大地水准面误差纬向分布图Fig.6 Co-latitudinal dependence of geoid error RMS of spherical harmonic solution and Slepian solution
6 结 论
利用卫星重力梯度数据恢复地球重力场的过程中,极空白问题使得球谐系数的低次项估计精度较低。Slepian函数能够在很大程度上解决面球谐函数的不正交问题,实现对地球重力场的有效恢复。本文对Slepian函数的数学性质进行详细分析,改进了求解的稳定性和求解效率,针对卫星重力梯度数据反演地球重力场,推导了引力梯度分量的Slepian函数实用展开式,最后通过仿真分析,就Slepian局部谱分析方法在卫星重力梯度数据确定地球重力位模型中的应用和前景进行了分析和讨论。研究表明:
Slepian函数在整个球面和球带上具有双正交性,可看做是同次面球谐函数的线性组合形式,其奇偶性与α-m的奇偶性相反。Slepian频谱能量随着纬度的增加逐渐减小,在两极地区达到最小,实现了将卫星观测信息最大化地聚集在非极空白区域,即保证了卫星轨道的测量特点与数据处理方法的一致性。Grünbaum算子的引入有效提高了Slepian方法求解的稳定性和效率。
Slepian方法的优良特性体现在Slepian频域内的地球重力场求解精度较之球谐域内的结果要高,但其对大地水准面空间分布的恢复精度贡献不明显。地球重力场和大地水准面精度的改进依赖于观测数据精度的提高以及观测数据频谱结构的改善。
[1] REIGBER C,LTIHR H,SCHWINTZER P.CHAMP Mission Status[J].Advances in Space Research,2002,30(2):129-134.
[2] TAPLEY B D,BETTADPUR S.The Gravity Recovery and Climate Experiment:Mission Overview and Early Results[J].Geophysical Research Letters,2004,31(9):1-6.
[3] ESA.Gravity Field and Steady-state Ocean Circulation Mission[M].Paris:ESA Publications Division,1999.
[4] SNEEUW N J,GELDEREN M V.The Polar Gap[J].Lecture Notes in Earth Sciences,1997,65:559-568.
[5] TSCHERNING C C,FORSBERG R,ALBERTELLA A,et al.The Polar Gap Problem:Space-wise Approaches to Gravity Field Determination in Polar Areas,from Eötvös to mGal[R].Copenhagen:University of Copenhagen,2000,331-336.
[6] DITMAR P,KUSCHE J,KLEES R.Computation of Spherical Harmonic Coefficients from Gravity Gradiometry Data to Be Acquired by the GOCE Satellite:Regularization Issues[J].Journal of Geodesy,2003,77(7-8):465-477.
[7] METZLER B.PAIL R.GOCE Data Processing:The Spherical Cap Regularization Approach[J].Studia Geophysica et Geodaetica,2005,49(4):441-462.
[8] XU Xinyu,LI Jiancheng,WANG Zhengtao,et al.The Simulation Research on the Tikhonov Regularization Applied in Gravity Field Determination of GOCE Satellite Mission[J].Acta Geodaetica et Cartographica Sinica,2010,39(5):465-470.(徐新禹,李建成,王正涛,等.Tikhonov正则化方法在GOCE重力场求解中的模拟研究[J].测绘学报,2010,39(5):465-470.)
[9] SLEPIAN D.Some Comments on Fourier-analysis,Uncertainty and Modeling[J].SIAM Rev,1983,25(3):379-393.
[10] ALBERTELLA A,SANSÒF,SNEEUW N.Band-limited Functions on a Bounded Spherical Domain:The Slepian Problem on the Sphere[J].Journal of Geodesy,1999,73(9):436-447.
[11] PAIL R,PLANKG,SCHUH W D.Spatially Restricted Data Distribution on the Sphere:The Method of Orthonormalized Functions and Applications[J].Journal of Geodesy,2001,75(1):44-56.
[12] MARK A W,SIMONS F J.Localized Spectral Analysis on the Sphere[J].Geophysical Journal International,2005,162(3):655-675.
[13] SIMONS F J,DAHLEN F A.Spherical Slepian Functions and the Polar Gap in Geodesy[J].Geophysical Journal International,2006,166(3):1039-1061.
[14] SIMONS F J,DAHLEN F A,WIECZOREK M A.Spatiospectral Concentration on a Sphere[J].SIAM Review,2006,48(3):504-536.
[15] SNEEUW N.Inclination Functions:Group Theoretical Background and a Recursive Algorithm[D].Delft:Delft University of Technology,1991.
[16] GILBER E N,SLEPIAN D.Doubly Orthogonal Concentrated Polynomials[J].SIAM Journal on Mathematical Analysis,1977,8(2):290-319.
[17] GRÜNBAUM F A,LONGHI L,PERLSTADT M.Differential Operators Commuting with Finite Convolution Integral Operators:Some Non-Abelian Examples[J].SIAM Journal on Applied Mathematics,1982,42(5):941-955.
[18] KOOP R.Global Gravity Field Modeling Using Satellite Gravity Gradiometry[D].Delft:Neth Geod Comm,1993.
[19] XU Xinyu.Study of Determining the Earth’s Gravity Field from Satellite Gravity Gradient and Satellite-to-Satellite Tracking Data[D].Wuhan:Wuhan University,2008.(徐新禹.卫星重力梯度及卫星跟踪卫星数据确定地球重力场的研究[D].武汉:武汉大学,2008.)
Slepian Localized Spectral Analysis of the Determination of the Earth’s Gravity Field Using Satellite Gravity Gradiometry Data
ZHU Guangbin1,LI Jiancheng2,WEN Hanjiang3,CHANG Xiaotao1,WANG Zhengtao2,ZOU Xiancai2
1.Satellite Surveying and Mapping Application Center,National Administration of Surveying,Mapping and Geoinformation,Beijing 100830,China;2.School of Geodesy and Geomatics,Wuhan University,Wuhan430079,China;3.Chinese Academy of Surveying and Mapping,Beijing100830,China
The Slepian localized spectral analysis method is introduced and its mathematical characteristics are analyzed.Grünbaum operator is introduced to improve the computational efficiency and stability.Then,the formulas of Slepian method for recovering the gravity field with satellite gravity gradiometry data are educed and numerical analysis are done.The results show that,Slepian function is orthogonal in both the sphere and the belt,and its spectral energy distribution characteristic is in accord with the orbit characteristic.Also,the accuracy of low order coefficients in Slepian domain is less influenced by polar gaps than that in spherical harmonic domain.However,the direct contribution of Slepian method to the improvement of geoid is limited.
satellite gravity gradiometry;gravity field;Slepian localized spectral analysis;polar gaps;surface spherical harmonics;Slepian function
ZHU Guangbin(1981—),male,PhD,majors in satellite geodesy.
ZHU Guangbin,LI Jiancheng,WEN Hanjiang,et al.Slepian Localized Spectral Analysis of the Determination of the Earth’s Gravity Field Using Satellite Gravity Gradiometry Data[J].Acta Geodaetica et Cartographica Sinica,2012,41(1):1-7.(朱广彬,李建成,文汉江,等.卫星重力梯度数据确定地球重力场的Slepian局部谱分析方法[J].测绘学报,2012,41(1):1-7.)
P223
A
1001-1595(2012)01-0001-07
国家863计划(2007AA12Z346);国家自然科学基金(40874012;40974016;41004007)
丛树平)
2011-01-13
2011-05-31
朱广彬(1981—),男,博士,研究方向为卫星大地测量。
E-mail:whu_gbzhu@hotmail.com
