基于分阶段GARCH模型中国B股市场波动性比较*
2012-01-03李克胜唐家银
李克胜,王 沁,唐家银
(西南交通大学数学学院,四川 成都 610031)
基于分阶段GARCH模型中国B股市场波动性比较*
李克胜,王 沁,唐家银
(西南交通大学数学学院,四川 成都 610031)
2001年2月19日,中国B股市场对国内居民正式开放,大量国内投资者涌入B股市场,对B股市场的风险结构产生了不可忽略的影响.对2001年2月19日前后2个阶段的深圳B股指数收益序列以及整个考察期内B股指数收益序列建立恰当的GARCH模型,比较模型的参数估计,从实证的角度证实了分阶段的合理性和必要性,同时发现中国B股市场的投资环境在逐渐变好,并且越来越遵循市场规范,正在向较成熟市场发展.
GARCH;风险结构;分阶段;非对称
中国股市经过近20年的发展,虽然取得了很大的成就,但是,它依然处于成长时期,表现出相当高的市场波动性,市场交易制度存在缺陷,使市场的不确定因素和风险增大.交易制度的不断改变给中国股市带来了较大的冲击,易造成股指收益序列的结构性变化.股指收益序列具有时变性,其波动特征可由GARCH模型来反映,若忽视了序列的结构性变点进行建模分析,所得到的结果不仅在精度上有问题,而且会导致伪波动持续性.因此,需要根据交易制度的改变进行系统的分阶段波动性的实证分析,以刻画相应的市场特征与行为,从而判断市场状态的变化以及进化.
GARCH模型在金融时间序列的波动性分析领域中得到了广泛的应用.阎海岩[1](2004)通过对沪深2市股指收益率的波动性建模发现,EGARCH(1,1)模型和EGARCH(1,1)-M模型都能很好地拟合数据,并且对2市股指收益率的波动性进行了预测;张广玉等[2]基于TARCH-M 模型对上海证券市场风险波动进行了实证分析,通过该模型很好地刻画出上海证券市场的风险波动;卢志红等[3]应用GARCH模型族对上海股市1997年前后2个阶段的股指收益率进行建模对比分析,发现沪市投资者正在从盲目投资逐渐转变为理性投资,并且沪市已经进入规范发展期;针对GARCH模型的变点问题,宿成建等[4]通过二分分段法结合西沃兹信息标准,找出了从1992—2002年上证和深证综合指数收益率序列中的所有波动性突变点,并对这些变点的经济意义进行了解释;王维国等[5]应用贝叶斯推断方法,研究了中国上证指数的突变点问题,指出上证指数序列在2005年11月附近存在突变点,并且对突变的原因给予了适当的解释;李绍刚等[6]利用ICSS算法,结合具体历史背景,检测并确定了2005—2009年的上证股指收益率的3个变点,通过分段建模,所得的结果消除了伪波动性.分阶段GARCH模型因能细致、客观、精确地捕捉金融数据的波动性,具有较大的应用前景.笔者正是从数据出发,进一步分析分阶段GARCH模型的优势.
中国股市的一个重大特点就是市场分割,即在市场里既有A股交易又有B股交易.2001年2月19日,中国证监会发布国内居民可以投资B股市场的决定[7],这种交易规则的改变对中国股市的波动性变化具有重大影响,尤其对B股市场而言,这种影响将会导致其股指收益序列产生结构性变点.因此,以2001年2月19日为分水岭,将考察的样本期分为2个阶段进行研究分析,以期从动态的角度,更细致地刻画波动性的演变.
1 GARCH族模型简介
广义自回归条件异方差(GARCH)模型能有效地刻画波动的聚集和持续性.GARCH(p,q)模型的结构如下[8]:
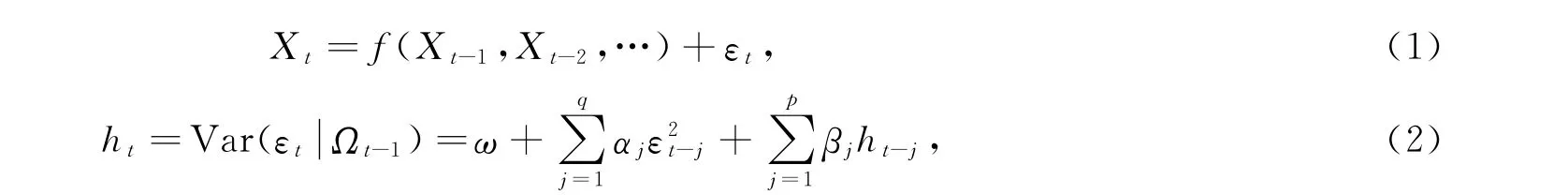
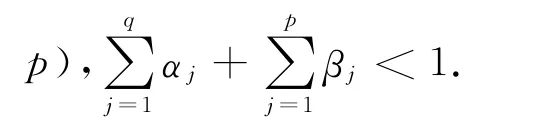
GARCH(p,q)模型将对称性加入到条件方差结构上,即条件方差对残差序列正的变化和负的变化的反应是对称的.它不能解释变量之间出现的负相关现象.对于股票市场,经常能观测到杠杆效应的存在,即与相同大小的利好消息相比,利空消息对波动性的影响更大,或利好消息引起的股价上涨远不及利空消息引起的股价下跌.最常用的非对称GARCH模型是指数广义自回归条件异方差(EGARCH)模型,其条件方差方程的表达式为[8]
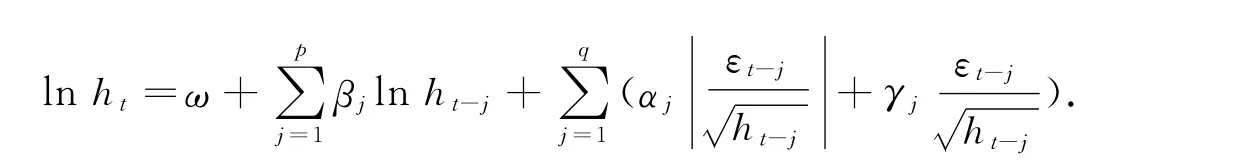
EGARCH模型的重要特征是在ht中引入了γ参数,使得干扰项εt取正负值时对ht有不同的影响,因此EGARCH模型可以很好地刻画金融市场中的非对称性情况.比如在股市,如果将利好消息看作对股价的正干扰,将利空消息看作对股价的负干扰,当存在j使得γj<0时,那么一个负干扰项(εt<0)所引起的ht的变化比相同程度的正干扰项(εt>0)所引起的ht的变化将更加剧烈,即市场上存在杠杆效应.另外,TARCH模型同样刻画不同性质的冲击对预期收益的影响,其条件方差方程为[9]

若γ>0,则市场存在杠杆效应.
2 实证研究
2.1 数据选取
已有大量文献从理论上证明了,由于1996年12月16日中国股市对证券交易实行10%的涨跌幅度限制,此后,中国股市已经由市场初创过渡调整期进入了规范发展期,因此,笔者选取的样本区间为1997年1月6日到2008年8月12日,采用深圳B股的日收盘价格指数.将检验的样本期分为2个阶段研究,第1阶段从1997年1月6日到2001年2月19日,第2阶段从2001年2月27日到2008年8月12日.对原始数据进行对数差分处理,得到日收益率序列rt=ln pt-ln pt-1,其中pt和pt-1分别表示第t日和第t-1日的指数收盘价.
2.2 数据的基本统计特征
将整个样本期内的收益率序列命名为S(t),对考察的样本按时间分阶段之后,2个阶段的收益率序列分别命名为S1(t)和S2(t).对序列S(t),S1(t)和S2(t)都采用无常数项和趋势性的ADF检验,其结果如表1所示.从表1可以看出,各序列的t统计量的值分别是-27.510 08,-27.687 66,-38.607 05,均小于各个显著性水平下的临界值,所以接受原假设,即不存在单位根.

表1 ADF检验结果
对序列S(t),S1(t)和S2(t)进行描述性统计,其结果如表2所示.从表2中可以看出各序列分布的特征,即尖峰厚尾和非正态性.另外,2阶段收益率序列的偏度均大于0,即存在右偏度现象,这说明深圳B股市场在交易行为方面存在“涨时放量,跌时缩量”的不成熟现象.这一现象与投资者的通常经验是相吻合的.但是,偏度由第1阶段的0.406 961减小为第2阶段的0.047 024,说明这种不成熟现象已经在很大程度上减弱了.

表2 描述性统计量
2.3 收益率序列的相关性分析
根据样本自相关系数和偏自相关系数的截尾性和拖尾性,结合Box-Jenkins建模思想,发现ARMA(3,3),AR(1),ARMA(1,3)模型分别为整体数据、第1阶段数据、第2阶段数据的最佳模型,其参数估计的结果如表3所示.从表3可以看出,整个检验期内的收益序列拟合结果的AIC值为-4.717 866,分阶段后,2阶段收益序列拟合结果的AIC值分别为-4.514 656和-4.888 248.很明显,第2阶段的AIC值小于整个检验期内的AIC值,也小于第1阶段的AIC值.这在一定程度上证明了分阶段的必要性.

表3 ARMA方程估计结果
2.4 基于GARCH族模型的研究
利用拉格朗日方法,检验残差序列是否具有异方差性,其具体结果如表4所示.从表4的结果可以看出,数据具有高阶异方差性,应采用GARCH模型建模.哈密尔顿等认为,GARCH(1,1)模型可以描述大多数的金融报酬时间序列,所以在波动性建模研究中被广泛采用.因此,笔者将采用GARCH(1,1),TARCH,EGARCH模型分别对深圳B股市场整个检验期内的样本和分阶段后的2个子样本进行建模研究并且对比分析,残差序列采用t-分布其结果如表5至表7所示.
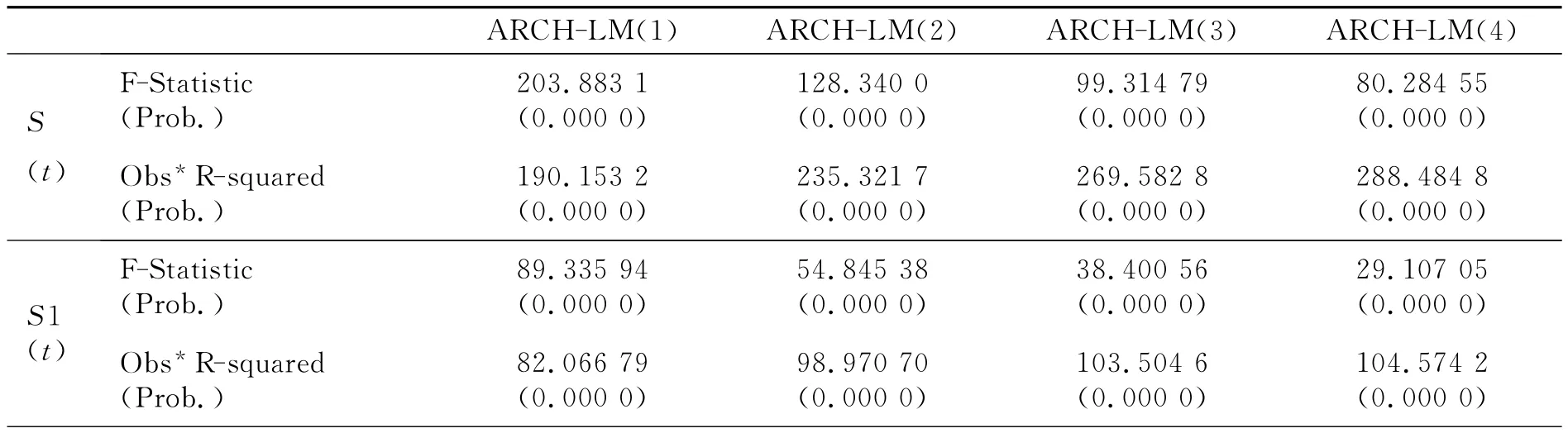
表4 ARCH-LM检验结果

续表

表5 整个检验期内收益序列的估计结果

表6 第1阶段收益序列的估计结果

表7 第2阶段收益序列的估计结果
分析以上估计结果,可以得出关于深圳B股市场的如下特点:
(1)在表5中,TARCH和EGARCH模型中γ值都没有显著性,说明深圳B股指数收益序列在整个考察期内不存在信息冲击的非对称性和杠杆效应.分阶段建模的结果显示,第1阶段的TARCH和EGARCH模型中γ值依然没有显著性,但是,第2阶段的TARCH和EGARCH模型中的γ值均在10%显著性水平下显著,并且TARCH模型的γ为正值,EGARCH模型的γ为负值,表明深圳B股指数收益序列在第2阶段存在显著的信息冲击的非对称性和杠杆效应.此外,由AIC值可以看出,第2阶段的3种GARCH模型的AIC值分别小于整个考察期内的3种GARCH模型的AIC值,也小于第1阶段的3种GARCH模型的AIC值,进一步证明了分阶段的合理性.
中国B股市场在对国内居民开放之前,每天的交易数量不大,加上上市公司发行的B股不能超过25%,这样一来,B股市场上的利坏消息对上市公司的影响很小,不会造成上市公司陷入财务危机,因此利坏消息对股票指数价格造成的负面影响有限,从而导致不能有效地察觉.所以,第1阶段不存在杠杆效应.当B股市场对国内居民开放之后,相当数量的国内股民投入B股市场,使每天的交易数量大增,以致B股市场上的利坏消息对上市公司的影响大大增加,这样就很有可能会导致上市公司陷入财务危机,因此上市公司的股票价格对B股市场上的利坏消息的反应变得越来越敏感了.所以,第2阶段存在显著的杠杆效应.
(2)由于第1阶段不存在信息冲击的非对称性和杠杆效应,因此应用GARCH(1,1)模型描述第1阶段的波动性已然足够.比较2阶段GARCH(1,1)模型可以看出,首先,系数α值减小了,β值增大了.这说明上一期有关波动的信息冲击对当前波动性的影响在减弱,而上一期波动性的预测对当前波动性的影响在加强.这种现象的存在说明与汇率有关的信息,对第1阶段的外国投资者有更为重要的影响,然而,当B股市场对国内居民开放后,这种影响就随之减弱了.对深圳B股市场上的外国投资者来说,这一变化是一个好消息.这也说明,深圳B股市场的投资环境在逐渐的变好.其次,第1阶段的衰减系数α+β值为1.55 544,大于1,表明第1阶段的GARCH过程是非平稳的,第2阶段的衰减系数α+β值为0.987 848,小于1,说明第2阶段的GARCH过程是平稳的.这样的结果进一步表明,深圳B股市场的波动逐渐趋缓,市场日趋成熟.
3 结语
准确地分析股票市场风险结构的变化,对广大股票投资者和股市管理层有极其重要的意义.建立合理的、符合市场实际的波动性模型来描述股市收益和波动性之间的准确关系,是理性分析市场风险的前提.基于GARCH(1,1),EGARCH,TARCH模型,对深圳B股市场2001年2月19日前后2个阶段的B股指数收益序列以及整个考察期内样本进行建模对比研究,从实证的角度证明了中国B股市场向国内居民开放对B股市场的健康发展产生了积极的影响.由实证研究的结果可以看出,中国的B股市场日趋成熟,投资环境逐渐变好,在资源配置方面变得越来越有效.
但是,中国股市同国外成熟股市相比依然存在差距.所以,今后监管层应该继续鼓励国内投资者在B股市场投资,使B股市场更加活跃.同时,应采取一些有效措施,进一步扩大A股市场的规模,使得中国股市不断地发展壮大.
[1]阎海岩.中国股市波动性研究 [J].统计与信息论坛,2004,19(5):40-43.
[2]张广玉,丁俊君.TARCH-M模型在测度上海证券市场风险中的应用 [J].中南财经政法大学学报,2004(5):113-116.
[3]卢志红,郑丕谔.GARCH 族模型在上海股市分阶段对比分析中的应用 [J].中国计量学院学报,2004,15(1):58-61.
[4]宿成建,陈 洁.应用变点模型来研究沪深股股市波动性突变行为 [J].重庆大学学报:自然科学版,2003,26(10):152-155.
[5]王维国,王 霞.关于我国上证指数突变点的研究 [J].统计与决策,2008(21):129-132.
[6]李绍刚,杨少华.基于GARCH 变点模型的上证收益率伪波动持续性研究 [J].价格月刊,2010(7):91-94.
[7] 人民网.中国证券市场大事记[1978—2008][EB/OL].[2008-09-24].http://30.people.com.cn/GB/134984/8097609.html.
[8]王 沁.时间序列分析及其应用[M].成都:西南交通大学出版社,2008:178-225.
(责任编辑 向阳洁)
Comparative Analysis of the Chinese B-Share Market Volatility in Phases Based on the GARCH Model
LI Ke-sheng,WANG Qin,TANG Jia-yin
(School of Mathematics,Southwest Jiaotong University,Chengdu 610031,China)
On Februay 19,2001,the B-share market of China was open to domestic residents legally.A larger number of domestic investors pour into the B-share market,which has produced dramatic effect on the risk structure of the B-share market.In this paper,the family of GARCH model was applied in modeling and analyzing Shenzhen B-share market,which was divided into two stages from Februay 19,2001 and the total review period samples.According to the comparison and study of the basic statistical results and the estimators of the model’s parameters of the return series,the necessity and rationality of phased modeling are proved.The phased GARCH model has found that the investment environment of Chinese B-share market has changed gradually for the better,and become more and more regulated,it is becoming a mature stock market.
GARCH;risk structure;phased;asymmetric
F224;F832.5
A
10.3969/j.issn.1007-2985.2012.03.007
1007-2985(2012)03-0022-05
2012-04-13
中央高校基本科研业务费专项资金资助(SWJTU12CX058)
李克胜(1988-),男,安徽芜湖人,西南交通大学数学学院硕士研究生,主要从事金融时间序列及其应用研究;王 沁(1973-),女,四川夹江人,西南交通大学数学学院副教授,理学硕士,工学博士,中国科学技术大学管理科学与工程博士后,主要从事Copula在统计学中的应用研究.
