基于加权L1最小化的图像小波域压缩感知重构*
2012-01-03张军
张 军
(广东工业大学信息工程学院,广东 广州510006)
基于加权L1最小化的图像小波域压缩感知重构*
张 军
(广东工业大学信息工程学院,广东 广州510006)
压缩感知理论因为能以少量的采样精确地重构原始信号而得到广泛关注.通过在压缩感知的框架下研究小波域图像重构问题,提出了一类小波域的加权l1最小化方法.该方法不仅利用了信号稀疏性的先验信息,而且在重构模型中,通过对不同小波子带上的系数施加不同的权重,从而整合了图像小波域的结构信息,与经典的压缩感知算法相比具有更好的信号可恢复性.仿真实验结果表明,选用该方法能够以更少的采样得到同等精度的重构图像,验证了该方法的有效性.
压缩感知;图像重构;小波;基追踪
在香农 -奈奎斯特(Shannon-Nyquist)采样定理的框架下,传统的数据获取技术经常陷入高速采样再大量丢弃的“怪圈”中,这个过程浪费了宝贵的采样与计算资源.近年来,Donoho[1]、Candes等[2]提出的压缩感知理论将传统的对信号的采样方式转变为对信息进行直接采样,从而可以以远低于奈奎斯特采样率的要求采样就获取信号的所有(或者绝大部分)信息.压缩感知理论极大地降低了信号采样、数据存储和传输的代价,被认为是对香农 -奈奎斯特采样理论的革命性突破.CS理论的主要思想来源于稀疏表示领域的这样一个结论:只要信号足够稀疏,就可以通过非线性优化的方法在欠定情况下有效地恢复原始信号.而对于n维原始信号S∈Rn×1,总能找到(至少对于自然界中的绝大多数信号是如此)某组正交基Ψ∈Rn×n,使得S在Ψ中的表示X=Ψ-1S是稀疏的.因此,只需要设计一组特定波形Φ∈Rm×n去感知信号S,即将信号S投影到给定波形上面,就可以采样到一组压缩数据Y.而压缩数据Y则包含了原始信号S的所有信息,可以利用某个重构方法实现对压缩数据Y解密得到稀疏信号X,最后利用逆变换

重构出原始信号S.在压缩感知中,Ψ,Φ分别称为变换矩阵与感知矩阵,而A=ΦΨ称为观测矩阵.近年来,压缩感知作为一种新的信号采样理论得到了广泛的关注[3-4].
在压缩感知的实现过程中,稀疏表示、非相关观测和信号的重构方法是3个关键的因素.其中信号的稀疏表示压缩感知的前提,非相关观测和信号重建是压缩感知的手段.为了精确地重构原始信号,Donoho等[5]提出了基追踪(Basis Pursuit,BP)算法.BP算法将信号重构转换成线性规划问题来进行求解,具有稳定、对噪声鲁棒的优点.另一类被广泛采样的信号重构方法是Mallat等[6]提出的匹配追踪(Match Pursuit,MP)算法及其后续的变种,例如正交匹配追踪(OMP)[7]与压缩采样匹配追踪(CoSaMP)算法[8]等.与BP算法相比,MP算法具有运算效率高的优点,但解的质量不如BP算法.之后,Vaswani等[9]整合信号的部分已知支撑信息,提出一个改进的BP算法:Modified-CS方法.而Khajehnejad等[10]发现,如果信号呈现非均匀稀疏性,那么对信号具有不同稀疏度的块施加不同的权重,将能有效提高算法的信号可恢复性.
笔者重点研究了基于压缩感知的图像小波域重构.众所周知,小波良好的时频局部化特性使得它能有效地稀疏表示数字图像,然而小波变换的特点使得图像在各小波子带下呈现显著的结构特性.基于这一现象,提出一类小波域的加权l1最小化方法并用于图像重构问题.
1 图像重构及小波域L1最小化方法
在图像的几类主要的稀疏表示域中,小波域因为其多分辨率特性与优异的稀疏化能力而得到了广泛的应用.二维图像通过按行(或者列)排列可以转化为一个n×1维信号S,对于某组小波基,可以构造一个大小为n×n的正交小波字典Ψ,则小波变换可以表示为(1)式的形式,其本质为得到信号S在字典Ψ下的稀疏表示X.如图1为Barbara图像(即信号S)及其在小波字典下的小波系数(即稀疏表示X),小波系数X的大部分分量的值接近于0,因此X是一个稀疏向量.根据小波域经典的压缩感知框架,通过构造m×n的矩阵Φ来观测信号S得到观测向量Y=ΦS+Z,其中Z为噪声或者系统误差,则BP算法是通过求解以下优化问题来求解稀疏向量X,从而利用(1)式重构原图像S:

现在以少量的采样(m≪n)就可以精确地重构X.

图1 Barbara图像及其小波系数
然而,小波变换所采用的金字塔算法的特点决定了图像的小波系数呈现出了结构上的规律性,例如对于图1中的小波系数,可以将其分为低频分量、第1层高频分量与第2层高频分量,根据小波分析理论易知,低频分量往往是比较大的系数,而第1,2层高频分量的系数的幅值依次降低,稀疏程度依次提高.这一特性可以通过在图像重构方法中加以利用,从而提高重构方法的信号可恢复性.
基于上述分析,提出小波域加权l1最小化方法:将图像小波系数的结构特征以权重的形式加以体现,稀疏度高的区域(例如图1中的第2层高频分量)施加大的权重,稀疏度低的区域(例如图1中的第1层高频分量)施加小的权重,而低频分量施加的权重为0.对于M层小波变换后的图像,具体的图像重构模型可以表示为
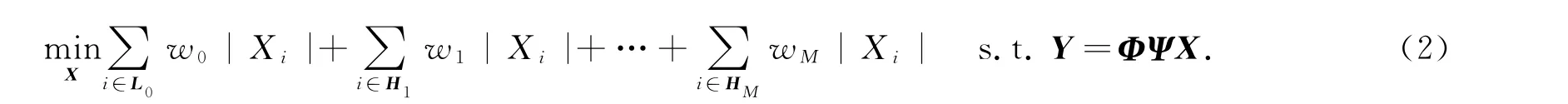
其中:w0=0,wM=1,wj=2j-M,j=1,…,M -1;L0表示低频带;Hj(j=1,2,…,M)表示第j个高频带.
2 仿真实验
为了验证小波域加权l1最小化方法的有效性,在欠定采样下重构图1中的Barbara图像.首先基于小波域多尺度CS框架采样Barbara图像:利用Haar小波来构建变换矩阵,同时生成一个随机高斯感知矩阵,所构建的观测矩阵对Barbara图像的3层小波域稀疏系数进行观测.在不同的采样率下,基于模型(2)来重建图像.显然,由本实验的采样方案可知,模型(2)中的M=3.为了检验模型(2)的性能,将模型(2)在不同采样率下的图像重构结果与经典的基追踪(BP)算法重建结果进行比较.在实验中,假设^X是重构图像,X是原图像,则选择
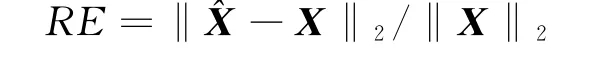

图2 重构误差曲线
作为重构误差(Reconstruction Error,ER)的衡量标准.Barbara图像在不同采样下的重构误差曲线如图2所示.
从图2可以看出,小波域加权l1最小化方法取得了比BP算法更小的重构误差,原因在于文中模型利用了小波域的结构信息.众所周知,BP算法在众多的经典压缩感知重构方法中具有最好的信号可恢复性,因此仿真实验验证了该方法的有效性.
3 结语
利用图像在小波域的结构信息,提出了一类用于图像重构的小波域加权l1最小化方法.因为除了信号稀疏性的先验信息外,该方法有效地整合了其他信息,所以能够取得很好的图像重构精度.在将来的工作中,将进一步从理论上分析文中模型的信号可恢复性,并研究相应的快速算法.
[1]DONOHO D L.Compressed Sensing[J].IEEE Trans.Inf.Theory,2006,52(4):1 289-1 306.
[2]CANDES E J,ROMBERG J,TAO T.Robust Uncertainty Principles:Exact Signal Reconstruction from Highly Incomplete Frequency Information[J].IEEE Trans.Inf.Theory,2006,52(2):489-509.
[3]CANDES E,WAKIN M.An Introduction to Compressive Sampling [J].IEEE Signal Process Mag.,2008,25(2):21-30.
[4]ROMBERG J.Imaging via Compressive Sampling[J].IEEE Signal Process Mag.,2008,25(2):14-20.
[5]CHEN S S,DONOHO D L,SAUNDERS M A.Atomic Decomposition by Basis Pursuit[J].SIAM Rev.,2001,43(1):129-159.
[6]MALLAT S,ZHANG Z.Matching Pursuits with Time-Frequency Dictionaries[J].IEEE Trans.Sig.Proc.,1993,41(12):3 397-3 415.
[7]NEEDELL D,TROPP J.CoSaMP:Iterative Signal Recovery from Incomplete and Inaccurate Samples[J].Applied and Computational Harmonic Analysis,2009,26(3):301-321.
[8]TROPP J,GILBERT A.Signal Recovery from Random Measurements via Orthogonal Matching Pursuit[J].IEEE Trans.Inf.Theory,2007,53(12):4 655-4 666.
[9]VASWANI N,LU W.Modified-CS:Modifying Compressive Sensing for Problems with Partially Known Support[J].IEEE Trans.Sig.Proc.,2010,58(9):4 595-4 607.
[10]KHAJEHNEJAD M,XU W,AVESTIMEHR S,et al.Analyzing Weighted l1Minimization for Sparse Recovery with Nonuniform Sparse Models[J].IEEE Trans.Sig.Proc.,2011,59(5):1 985-2 001.
(责任编辑 向阳洁)
Weighted Minimization for Compressive Sensing Image Reconstruction in Wavelet Domain
ZHANG Jun
(School of Information Engineering,Guangdong University of Technology,Guangzhou 510006,China)
Compressive sensing has
much attention in the signal processing field for it can reconstruct a signal or image from surprisingly few samples.In this paper,the author investigates the wavelet domain image reconstruction problem and proposes a weighted liminimization algorithm to reconstruct the images.The proposed method utilizes not only the sparsity of signals,but also incorporates the structure information of images in wavelet domain.Hence,compared with the classical compressive sensing algorithm,the proposed method has better recoverability.Simulation results show that the proposed method has achieved the same equality image from few samples,which demonstrates the validity of the proposed method.
compressive sensing;image reconstruction;wavelet;basis pursuit
TN911.72
A
10.3969/j.issn.1007-2985.2012.04.019
1007-2985(2012)04-0083-04
2012-02-24
国家自然科学基金资助项目(60901027)
张 军(1979-),男,湖南新化人,广东工业大学信息工程学院讲师,博士,主要从事压缩感知、稀疏表示及其在信号处理中的应用研究.
